- Research Article
- Open access
- Published:
Dynamical Properties in a Fourth-Order Nonlinear Difference Equation
Advances in Difference Equations volume 2010, Article number: 679409 (2010)
Abstract
The rule of trajectory structure for fourth-order nonlinear difference equation  ,
,  where
where  and the initial values
and the initial values  , is described clearly out in this paper. Mainly, the lengths of positive and negative semicycles of its nontrivial solutions are found to occur periodically with prime period 15. The rule is
, is described clearly out in this paper. Mainly, the lengths of positive and negative semicycles of its nontrivial solutions are found to occur periodically with prime period 15. The rule is  in a period. By utilizing this rule its positive equilibrium point is verified to be globally asymptotically stable.
in a period. By utilizing this rule its positive equilibrium point is verified to be globally asymptotically stable.
1. Introduction
In this paper we consider the following fourth-order nonlinear difference equation:

where  and the initial values
and the initial values 
When  , (1.1) becomes the trivial case
, (1.1) becomes the trivial case  ,
,  Hence, we will assume in the sequel that
Hence, we will assume in the sequel that  .
.
When  , (1.1) is not a rational difference equation but a nonlinear one. So far, there have not been any effective general methods to deal with the global behavior of nonlinear difference equations of order greater than one. Therefore, to study the qualitative properties of nonlinear difference equations with higher order is theoretically meaningful.
, (1.1) is not a rational difference equation but a nonlinear one. So far, there have not been any effective general methods to deal with the global behavior of nonlinear difference equations of order greater than one. Therefore, to study the qualitative properties of nonlinear difference equations with higher order is theoretically meaningful.
In this paper, it is of key for us to find that the lengths of positive and negative semi-cycles of nontrivial solutions of (1.1) occur periodically with prime period 15 with the rule  ,
, ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and in a period. With the help of this rule and utilizing the monotonicity of solution the positive equilibrium point of the equation is verified to be globally asymptotically stable.
and in a period. With the help of this rule and utilizing the monotonicity of solution the positive equilibrium point of the equation is verified to be globally asymptotically stable.
Essentially, we derive the following results for solutions of (1.1).
Theorem CL.
The rule of the trajectory structure of (1.1) is that all of its solutions asymptotically approach its equilibrium; furthermore, any one of its solutions is either
-
(1)
eventually trivial
-
(2)
nonoscillatory and eventually negative (i.e.,
 ) or
) or -
(3)
strictly oscillatory with the lengths of positive and negative semi-cycles periodically successively occurring with prime period 15 and the rule to be
 ,
,  ,
,  ,
,  ,
,  ,
, 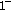 ,
,  ,
,  in a period.
in a period.
It follows from the results stated below that Theorem CL is true.
It is easy to see that the positive equilibrium  of (1.1) satisfies
of (1.1) satisfies

from which one can see that (1.1) has a unique equilibrium 
In the following, we state some main definitions used in this paper.
Definition 1.1.
A positive semi-cycle  of a solution of (1.1) consists of a "string" of terms
of a solution of (1.1) consists of a "string" of terms  , all greater than or equal to the equilibrium
, all greater than or equal to the equilibrium  , with
, with  and
and  such that
such that

A negative semi-cycle of a solution  of (1.1) consists of a "string" of term
of (1.1) consists of a "string" of term  , all less than
, all less than  , with
, with  and
and  such that
such that

The length of a semi-cycle is the number of the total terms contained in it.
Definition 1.2.
A solution  of (1.1) is said to be eventually trivial if
of (1.1) is said to be eventually trivial if  is eventually equal to
is eventually equal to  ; Otherwise, the solution is said to be nontrivial. A solution
; Otherwise, the solution is said to be nontrivial. A solution  of (1.1) is said to be eventually positive (negative) if
of (1.1) is said to be eventually positive (negative) if  is eventually greater (less) than
is eventually greater (less) than  .
.
For the other concepts in this paper and related work, see [1–3] and [4–11], respectively.
2. Three Lemmas
Before drawing a qualitatively clear picture for the solutions of (1.1), we first establish three basic lemmas which will play key roles in the proof of our main results.
Lemma 2.1.
A solution  of (1.1) is eventually trivial if and only if
of (1.1) is eventually trivial if and only if

Proof.
Sufficiency. Assume that (2.1) holds. Then it follows from (1.1) that the following conclusions hold:
-
(i)
if
 , then
, then  for
for 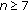 ;
; -
(ii)
if
 , then
, then 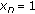 for
for 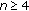 ;
; -
(iii)
if
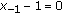 , then
, then 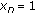 for
for 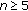 ;
; -
(iv)
if
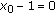 , then
, then  for
for 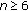 .
.
Necessity. Conversely, assume that

Then one can show that

Assume the contrary that for some  ,
,

Clearly,

which implies that  , which contradicts (2.4).
, which contradicts (2.4).
Remark 2.2.
Lemma 2.1 actually demonstrates that a solution  of (1.1) is eventually nontrivial if and only if
of (1.1) is eventually nontrivial if and only if

Therefore, if a solution  is nontrivial, then
is nontrivial, then  for
for  .
.
Lemma 2.3.
Let  be a nontrivial positive solution of (1.1). Then the following conclusions are true:
be a nontrivial positive solution of (1.1). Then the following conclusions are true:
-
(a)
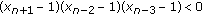 for
for 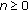 ;
; -
(b)
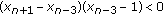 for
for 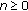 .
.
Proof.
In view of (1.1), we can see that

from which inequalities (a) and (b) follow. So the proof is complete.
Lemma 2.4.
There exist nonoscillatory solutions of (1.1), which must be eventually negative. There do not exist eventually positive non-oscillatory solutions of (1.1).
Proof.
Consider a solution of (1.1) with  ,
,  , and
, and  . We then know from Lemma 2.3(a) that
. We then know from Lemma 2.3(a) that  for
for  . So, this solution is just a non-oscillatory solution, and furthermore, eventually negative. Suppose that there exist eventually positive nonoscillatory solutions of (1.1). Then, there exists a positive integer
. So, this solution is just a non-oscillatory solution, and furthermore, eventually negative. Suppose that there exist eventually positive nonoscillatory solutions of (1.1). Then, there exists a positive integer  such that
such that  for
for  . Thereout, for
. Thereout, for  ,
,  . This contradicts Lemma 2.3(a). So, there do not exist eventually positive non-oscillatory solutions of (1.1), as desired.
. This contradicts Lemma 2.3(a). So, there do not exist eventually positive non-oscillatory solutions of (1.1), as desired.
3. Main Results and Their Proofs
First we analyze the structure of the semi-cycles of nontrivial solutions of (1.1). Here we confine us to consider the situation of the strictly oscillatory solution of (1.1).
Theorem 3.1.
Let  be any strictly oscillatory solution of (1.1). Then, the lengths of positive and negative semi-cycles of the solution periodically successively occur with prime period 15. And in a period, the rule is
be any strictly oscillatory solution of (1.1). Then, the lengths of positive and negative semi-cycles of the solution periodically successively occur with prime period 15. And in a period, the rule is  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Proof.
By Lemma 2.3(a), one can see that the length of a positive semi-cycle is not larger than 4, whereas, the length of a negative semi-cycle is at most 3. Based on the strictly oscillatory character of the solution, we see, for some integer  , that one of the following four cases must occur.
, that one of the following four cases must occur.
Case 1.
 ,
,  ,
,  ,
,  .
.
Case 2.
 ,
,  ,
,  ,
,  .
.
Case 3.
 ,
,  ,
,  ,
,  .
.
Case 4.
 ,
,  ,
,  ,
,  .
.
If Case 1 occurs, it follows from Lemma 2.3(a) that  ,
,  ,
, ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, , which means that the rule for the lengths of positive and negative semi-cycles of the solution of (1.1) to successively occur is
, which means that the rule for the lengths of positive and negative semi-cycles of the solution of (1.1) to successively occur is 
If Case 2 happens, then Lemma 2.3(a) tells us that  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, . This shows that the rule for the numbers of terms of positive and negative semi-cycles of the solution of (1.1) to successively occur still is
. This shows that the rule for the numbers of terms of positive and negative semi-cycles of the solution of (1.1) to successively occur still is 
If Case 3 happens, then Lemma 2.3(a) implies that  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, This shows that the rule for the numbers of terms of positive and negative semi-cycles of the solution of (1.1) to successively occur still is
This shows that the rule for the numbers of terms of positive and negative semi-cycles of the solution of (1.1) to successively occur still is 
If Case 4 happens, then it is to be seen from Lemma 2.3(a) that  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, . This shows that the rule for the numbers of terms of positive and negative semi-cycles of the solution of (1.1) to successively occur still is
. This shows that the rule for the numbers of terms of positive and negative semi-cycles of the solution of (1.1) to successively occur still is 
Hence, the proof is complete.
Now, we present the global asymptotical stable results for (1.1).
Theorem 3.2.
Assume that  . Then the unique positive equilibrium of (1.1) is globally asymptotically stable.
. Then the unique positive equilibrium of (1.1) is globally asymptotically stable.
Proof.
When  , (1.1) is trivial. So, we only consider the case
, (1.1) is trivial. So, we only consider the case  and prove that the positive equilibrium point
and prove that the positive equilibrium point  of (1.1) is both locally asymptotically stable and globally attractive. The linearized equation of (1.1) about the positive equilibrium
of (1.1) is both locally asymptotically stable and globally attractive. The linearized equation of (1.1) about the positive equilibrium  is
is

By virtue of [3, Remark  , page 13],
, page 13],  is locally asymptotically stable. It remains to be verified that every positive solution
is locally asymptotically stable. It remains to be verified that every positive solution  of (1.1) converges to
of (1.1) converges to  as
as  . Namely, we want to prove that
. Namely, we want to prove that

If the initial values of the solutions satisfy (2.1), that is to say, the solution is a trivial solution, then Lemma 2.1 says that the solution is eventually equal to  and of course (3.2) holds.
and of course (3.2) holds.
If the solution is a nontrivial solution, then we can further divide the solution into two cases.
-
(a)
non-oscillatory solution;
-
(b)
oscillatory solution.
If Case  happens, then it follows from Lemma 2.3 that the solution is actually an eventually negative one. According to Lemma 2.3(b), we see that
happens, then it follows from Lemma 2.3 that the solution is actually an eventually negative one. According to Lemma 2.3(b), we see that  ,
,  ,
,  and
and  are eventually increasing and bounded from the upper by the constant
are eventually increasing and bounded from the upper by the constant  . So the limits
. So the limits

exist and are finite. Noting that

and taking the limits on both sides of the above equalities, respectively, one may obtain

Solving these equations, we get  , which shows that (3.2) is true.
, which shows that (3.2) is true.
If case (b) happens, the solution is strictly oscillatory.
Consider now  to be strictly oscillatory about the positive equilibrium point
to be strictly oscillatory about the positive equilibrium point  of (1.1). By virtue of Theorem 3.1, one understands that the lengths of positive and negative semi-cycles of the solution periodically successively occur, and in a period, the rule is
of (1.1). By virtue of Theorem 3.1, one understands that the lengths of positive and negative semi-cycles of the solution periodically successively occur, and in a period, the rule is 
For simplicity, for some integer  , we denote by
, we denote by  the terms of a positive semi-cycle of length four, followed by
the terms of a positive semi-cycle of length four, followed by  negative semi-cycle with length three, then a positive semi-cycle
negative semi-cycle with length three, then a positive semi-cycle  , a negative semi-cycle
, a negative semi-cycle  , a positive semi-cycle
, a positive semi-cycle  , a negative semi-cycle
, a negative semi-cycle  , a positive semi-cycle
, a positive semi-cycle  , and a negative semi-cycle
, and a negative semi-cycle  . Namely, the rule for the lengths of negative and positive semi-cycles to occur successively can be periodically expressed as follows:
. Namely, the rule for the lengths of negative and positive semi-cycles to occur successively can be periodically expressed as follows: ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and 
From Lemma 2.3(b), we may immediately obtain the following results:
-
(i)
 ;
; 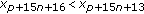 ;
; -
(ii)
 ;
; 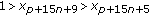 .
.
Also, the following inequalities hold:
-
(iii)
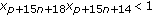 ;
; 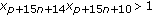 ;
; -
(iv)
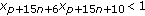 ;
;  ;
; -
(v)
 ;
; -
(vi)
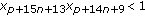 ;
; 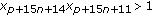 ;
; 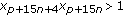 ;
; -
(vii)
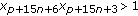 ;
; 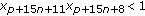 .
.
In fact, from the observation that

we know that the first inequality in (iii) is true. The other inequalities in (iii)–(vi) can be similarly proved. Noticing that  and from that the observation
and from that the observation

we know that the first inequality in (vii) holds. The other inequality in (vii) can be analogously proved.
Combining the above inequalities, one can derive that



It follows from (3.8) that  is decreasing with lower bound 1. So, the limit
is decreasing with lower bound 1. So, the limit

exists and is finite. Accordingly, by view of (3.8), we obtain

It is easy to see from (3.9) that  is decreasing with lower bound 1. So, the limit
is decreasing with lower bound 1. So, the limit

exists and is finite. Thereout, in light of (3.9), one has

It follows from (3.10) that  is decreasing with lower bound 1. So, the limit
is decreasing with lower bound 1. So, the limit

exists and is finite. Accordingly, by view of (3.10), we obtain

Taking the limits on both sides of  , one has
, one has  , which gives rise to
, which gives rise to  . We further obtain from (i) and (3.12) that
. We further obtain from (i) and (3.12) that

Hence,  . Therefore,
. Therefore,

It is easy to derive from (v) that  . Noticing that
. Noticing that  , one can see that
, one can see that  .
.
Similarly, taking the limits on both sides of  , one has
, one has  . Finally, by taking the limits on both sides of
. Finally, by taking the limits on both sides of  , one has
, one has  .
.
Up to now, we have shown that

So, the proof for Theorem 3.2 is complete.
Remark 3.3.
One can see from the process of proofs stated previously that these results in this paper also hold for  .
.
References
Agarwal RP: Difference Equations and Inequalities. 1st edition. Marcel Dekker, New York, NY, USA; 1992.
Agarwal RP: Difference Equations and Inequalities. 2nd edition. Marcel Dekker, New York, NY, USA; 2000.
Kocić VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and Its Applications. Volume 256. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+228.
Kulenović MRS, Ladas G, Prokup NR: A rational difference equation. Computers and Mathematics with Applications 2001,41(5-6):671-678. 10.1016/S0898-1221(00)00311-4
Amleh AM, Grove EA, Ladas G, Georgiou DA:On the recursive sequence
 . Journal of Mathematical Analysis and Applications 1999,233(2):790-798. 10.1006/jmaa.1999.6346
. Journal of Mathematical Analysis and Applications 1999,233(2):790-798. 10.1006/jmaa.1999.6346Li XY: Global behavior for a fourth-order rational difference equation. Journal of Mathematical Analysis and Applications 2005,312(2):555-563. 10.1016/j.jmaa.2005.03.097
Li XY: The rule of trajectory structure and global asymptotic stability for a nonlinear difference equation. Applied Mathematics Letters 2006,19(11):1152-1158. 10.1016/j.aml.2006.01.001
Li XY, Agarwal RP: The rule of trajectory structure and global asymptotic stability for a fourth-order rational difference equation. Journal of the Korean Mathematical Society 2007,44(4):787-797. 10.4134/JKMS.2007.44.4.787
Li XY, Zhu DM, Zhou Y, Deng G-Y: Oscillation and nonoscillation for nonlinear neutral difference equations with continuous arguments. International Journal of Nonlinear Sciences and Numerical Simulation 2002,3(2):153-160. 10.1515/IJNSNS.2002.3.2.153
Gibbons CH, Kulenović MRS, Ladas G:On the recursive sequence
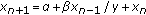 . Mathematical Sciences Research Hot-Line 2000,4(2):1-11.
. Mathematical Sciences Research Hot-Line 2000,4(2):1-11.Kulenović MRS, Ladas G, Martins LF, Rodrigues IW:The dynamics of
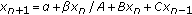 : facts and conjectures. Computers and Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7
: facts and conjectures. Computers and Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7
Acknowledgment
This work is partly supported by NNSF of China (grant: 10771094) and the Foundation for the Innovation Group of Shenzhen University (grant: 000133).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, Y., Li, X. Dynamical Properties in a Fourth-Order Nonlinear Difference Equation. Adv Differ Equ 2010, 679409 (2010). https://doi.org/10.1155/2010/679409
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/679409
 ) or
) or ,
,  ,
,  ,
,  ,
,  ,
, 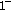 ,
,  ,
,  in a period.
in a period. , then
, then  for
for 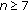 ;
; , then
, then 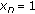 for
for 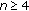 ;
;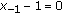 , then
, then 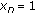 for
for 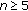 ;
;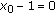 , then
, then  for
for 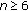 .
.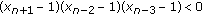 for
for 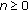 ;
;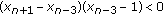 for
for 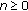 .
. ;
; 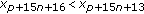 ;
; ;
; 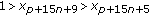 .
.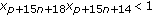 ;
; 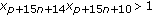 ;
;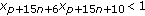 ;
;  ;
; ;
;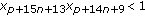 ;
; 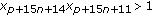 ;
; 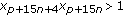 ;
;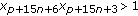 ;
; 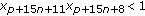 .
. . Journal of Mathematical Analysis and Applications 1999,233(2):790-798. 10.1006/jmaa.1999.6346
. Journal of Mathematical Analysis and Applications 1999,233(2):790-798. 10.1006/jmaa.1999.6346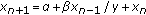 . Mathematical Sciences Research Hot-Line 2000,4(2):1-11.
. Mathematical Sciences Research Hot-Line 2000,4(2):1-11.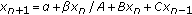 : facts and conjectures. Computers and Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7
: facts and conjectures. Computers and Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7