- Research Article
- Open access
- Published:
Existence Theorems for First-Order Equations on Time Scales with  -Carathéodory Functions
-Carathéodory Functions
Advances in Difference Equations volume 2010, Article number: 650827 (2010)
Abstract
This paper concerns the existence of solutions for two kinds of systems of first-order equations on time scales. Existence results for these problems are obtained with new notions of solution tube adapted to these systems. We consider the general case where the right member of the system is  -Carathéodory and, hence, not necessarily continuous.
-Carathéodory and, hence, not necessarily continuous.
1. Introduction
In this paper, we establish existence results for the following systems:


Here,  is an arbitrary compact time scale where we note
is an arbitrary compact time scale where we note  ,
,  , and
, and  . Moreover,
. Moreover,  is a
is a  -Carathéodory function and
-Carathéodory function and  denotes one of the following boundary conditions:
denotes one of the following boundary conditions:


In the literature, this kind of problem was mainly treated for  . The existence of extremal solutions was established in [1, 2]. Moreover, some existence results in the particular case where the time scale is a discrete set (difference equation) were obtained with the lower and upper solution method as in [3, 4]. In this paper, we introduce a new notion which generalizes to systems of first-order equations on time scales the notions of lower and upper solutions. This notion called solution tube for system (1.1) (resp., (1.2)) will be useful to get a new existence result for (1.1) (resp., (1.2)). Our notion of solution tube is in the spirit of the notion of solution tube for systems of first-order differential equations introduced in [5]. Our notion is new even in the case of systems of first-order difference equations. In this case, we generalize to the systems a result of [3] for equation (1.2).
. The existence of extremal solutions was established in [1, 2]. Moreover, some existence results in the particular case where the time scale is a discrete set (difference equation) were obtained with the lower and upper solution method as in [3, 4]. In this paper, we introduce a new notion which generalizes to systems of first-order equations on time scales the notions of lower and upper solutions. This notion called solution tube for system (1.1) (resp., (1.2)) will be useful to get a new existence result for (1.1) (resp., (1.2)). Our notion of solution tube is in the spirit of the notion of solution tube for systems of first-order differential equations introduced in [5]. Our notion is new even in the case of systems of first-order difference equations. In this case, we generalize to the systems a result of [3] for equation (1.2).
Some papers treat the existence of solutions to systems of first-order equations on time scales. Existence results are obtained in [6, 7] under hypothesis different from ours. However, some particular cases obtained in [7] are corollaries of our existence result for problem (1.1). Also, our existence results treat the case where the right members in (1.1) and (1.2) are  -Carathéodory functions which are more general than continuous functions used for systems studied in [6, 7]. Let us mention that existence of extremal solutions for infinite systems of first-order equations of time scale with
-Carathéodory functions which are more general than continuous functions used for systems studied in [6, 7]. Let us mention that existence of extremal solutions for infinite systems of first-order equations of time scale with  -Carathéodory functions is established in [8].
-Carathéodory functions is established in [8].
This paper is organized as follows. The third section presents an existence result for the problem (1.1), and in the last section, we obtain an existence theorem for the problem (1.2). We start with some notations, definitions, and results on time scales equations which are used throughout this paper.
2. Preliminaries and Notations
In this section, we establish notations, definitions, and results on equations on time scales which are used throughout this paper. The reader may consult [9–11] and the references therein to find the proofs and to get a complete introduction to this subject.
Let  be a time scale, which is a closed nonempty subset of
be a time scale, which is a closed nonempty subset of  . For
. For  , we define the forward jump operator
, we define the forward jump operator (resp., the backward jump operator
(resp., the backward jump operator ) by
) by  (resp., by
(resp., by  ). We suppose that
). We suppose that  if
if  is the maximum of
is the maximum of  and that
and that  if
if  is the minimum of
is the minimum of  . We say that
. We say that  is right-scattered (resp., left-scattered) if
is right-scattered (resp., left-scattered) if  (resp., if
(resp., if  ). We say that
). We say that  is isolated if it is right-scattered and left-scattered. Also, if
is isolated if it is right-scattered and left-scattered. Also, if  and
and  , we say that
, we say that  is right-dense. If
is right-dense. If  and
and  , we say that
, we say that  is left dense. Points that are right dense and left dense are called dense. The graininess function
is left dense. Points that are right dense and left dense are called dense. The graininess function is defined by
is defined by  .
.
If  has a left-scattered maximum, then
has a left-scattered maximum, then  . Otherwise,
. Otherwise,  . In summary,
. In summary,

If  is bounded, then
is bounded, then  where
where  .
.
Definition 2.1.
Assume  is a function and let
is a function and let  . We say that
. We say that  is
is  -differentiable at
-differentiable at  if there exists a vector
if there exists a vector  such that for all
such that for all  , there exists a neighborhood
, there exists a neighborhood  of
of  , where
, where

for every  . We call
. We call  the
the  -derivative of
-derivative of  at
at  . If
. If  is
is  -differentiable at
-differentiable at  for every
for every  , then
, then  is called the
is called the  -derivative of
-derivative of  on
on  .
.
Theorem 2.2.
Assume  is a function and let
is a function and let  . Then, we have the following.
. Then, we have the following.
-
(i)
If
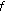 is
is  -differentiable at
-differentiable at 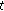 , then
, then 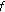 is continuous at
is continuous at 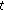 .
. -
(ii)
If
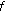 is continuous at
is continuous at 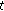 and if
and if 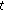 is right-scattered, then
is right-scattered, then 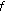 is
is 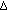 -differentiable at
-differentiable at 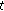 and
and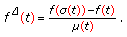 (2.3)
(2.3) -
(iii)
If
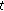 is right dense, then
is right dense, then 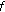 is
is 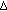 -differentiable at
-differentiable at  if and only if
if and only if 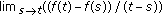 exists in
exists in 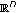 . In this case,
. In this case, 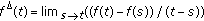 .
. -
(iv)
If
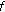 is
is 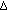 -differentiable at
-differentiable at  , then
, then 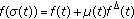 .
.
Theorem 2.3.
If  are
are  -differentiable at
-differentiable at  , then
, then
-
(i)
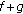 is
is 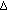 -differentiable at
-differentiable at 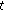 and
and 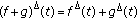 ,
, -
(ii)
 is
is 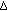 -differentiable at
-differentiable at  for every
for every 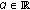 and
and 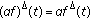 ,
, -
(iii)
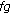 is
is 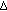 -differentiable at
-differentiable at  and
and 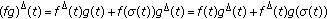 ,
, -
(iv)
If
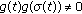 , then
, then 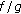 is
is  -differentiable at
-differentiable at 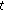 and
and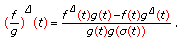 (2.4)
(2.4)
The next result is an adaptation of Theorem 1.87 in [10].
Theorem 2.4.
Let  be an open set of
be an open set of  and
and  a right-dense point. If
a right-dense point. If  is
is  -differentiable at
-differentiable at  and if
and if  is differentiable at
is differentiable at  , then
, then  is
is  -differentiable at
-differentiable at  and
and  .
.
Example 2.5.
Assume is
is - differentiable at
- differentiable at . We know that
. We know that is differentiable. If
is differentiable. If , by the previous theorem, we have
, by the previous theorem, we have .
.
Definition 2.6.
A function  is called
is called  -continuous provided it is continuous at right-dense points in
-continuous provided it is continuous at right-dense points in  and its left-sided limits exist (finite) at left-dense points in
and its left-sided limits exist (finite) at left-dense points in  . The set of
. The set of  -continuous functions
-continuous functions  is denoted by
is denoted by  . The set of functions
. The set of functions  that are
that are  -differentiable and whose
-differentiable and whose  -derivative is
-derivative is  -continuous is denoted by
-continuous is denoted by  .
.
It is possible to define a theory of measure and integration for an arbitrary bounded time scale  where
where  . We recall the notion of
. We recall the notion of  -measure as introduced in chapter 5 of [9]. Define
-measure as introduced in chapter 5 of [9]. Define  the family of intervals of
the family of intervals of  of the form
of the form

where  and
and  . The interval
. The interval  is understood as the empty set. An outer measure
is understood as the empty set. An outer measure  on
on  is defined as follows: for
is defined as follows: for  ,
,

Definition 2.7.
A set  is said to be
is said to be  -measurable if for every set
-measurable if for every set  ,
,

Now, denote

The Lebesgue -measure on
-measure on  , denoted by
, denoted by  , is the restriction of
, is the restriction of  to
to  . We get a complete measurable space with
. We get a complete measurable space with  .
.
With this definition of complete measurable space for a bounded time scale  , we can define the notions of
, we can define the notions of  -measurability and
-measurability and  -integrability for functions
-integrability for functions  following the same ideas of the theory of Lebesgue integral. We omit here these definitions that an interested reader can find in [12]. We only present definitions and results which will be useful for this paper.
following the same ideas of the theory of Lebesgue integral. We omit here these definitions that an interested reader can find in [12]. We only present definitions and results which will be useful for this paper.
Definition 2.8.
Let  be a
be a  -measurable set and
-measurable set and  be a
be a  -measurable function. We say that
-measurable function. We say that  provided
provided

We say that a  -measurable function
-measurable function  is in the set
is in the set  provided
provided

for each of its components  .
.
Proposition 2.9.
Assume  . Then,
. Then,

Many results of integration theory are established for measurable functions  where
where  is a complete measurable space. These results are in particular true for the measurable space
is a complete measurable space. These results are in particular true for the measurable space  . We recall two results of the theory of integration adapted to our situation.
. We recall two results of the theory of integration adapted to our situation.
Theorem 2.10 (Lebesgue-dominated convergence Theorem).
Let  be a sequence of functions in
be a sequence of functions in  . If there exists a function
. If there exists a function  such that
such that 
 -a.e.
-a.e.  and if there exists a function
and if there exists a function  such that
such that 
 -a.e.
-a.e.  and for every
and for every  , then
, then  in
in  .
.
Theorem 2.11.
The set  is a Banach space endowed with the norm
is a Banach space endowed with the norm  .
.
The following results were obtained in [12] where a useful relation between the  -measure on
-measure on  (resp.,
(resp.,  -integral on
-integral on  ) and the Lebesgue measure (
) and the Lebesgue measure ( ) on
) on  (resp., Lebesgue integral on
(resp., Lebesgue integral on  ) is established. To establish these results, the authors of [12] prove that the set of right-scattered points of
) is established. To establish these results, the authors of [12] prove that the set of right-scattered points of  is at most countable. Then, there are a set of index
is at most countable. Then, there are a set of index  and a set
and a set  such that
such that  .
.
Proposition 2.12.
Let  . Then,
. Then,  is
is  -measurable if and only if
-measurable if and only if  is Lebesgue measurable. In such a case, the following properties hold for every
is Lebesgue measurable. In such a case, the following properties hold for every  -measurable set A.
-measurable set A.
-
(i)
If
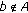 , then
, then (2.12)
(2.12) -
(ii)
 if and only if
if and only if  and A has no right-scattered points. Here,
and A has no right-scattered points. Here,  .
.
To establish the relation between  -integration on
-integration on  and Lebesgue integration on a real compact interval, the function
and Lebesgue integration on a real compact interval, the function  is extended to
is extended to  in the following way.
in the following way.

Theorem 2.13.
Let  be a
be a  -measurable set such that
-measurable set such that  and let
and let  . Let
. Let  be a
be a  -measurable function and
-measurable function and  its extension on
its extension on  . Then,
. Then,  is
is  -integrable on
-integrable on  if and only if
if and only if  is Lebesgue integrable on
is Lebesgue integrable on  . In such a case, one has
. In such a case, one has

Also, the function  can be extended on
can be extended on  in another way. Define
in another way. Define  by
by

Definition 2.14.
A function  is said to be absolutely continuous on
is said to be absolutely continuous on if for every
if for every  , there exists a
, there exists a  such that if
such that if  with
with  is a finite pairwise disjoint family of subintervals of
is a finite pairwise disjoint family of subintervals of  satisfying
satisfying  , then
, then  .
.
The three following results were obtained in [13].
Lemma 2.15.
If  is differentiable at
is differentiable at  , then
, then  is
is  -differentiable at
-differentiable at  and
and  .
.
Theorem 2.16.
Consider a function  and its extension
and its extension  . Then,
. Then,  is absolutely continuous on
is absolutely continuous on  if and only if
if and only if  is absolutely continuous on
is absolutely continuous on  .
.
Theorem 2.17.
A function  is absolutely continuous on
is absolutely continuous on  if and only if
if and only if  is
is  -differentiable
-differentiable  -almost everywhere on
-almost everywhere on  ,
,  and
and

We also recall the Banach Lemma.
Lemma 2.18.
Let  be a Banach space and
be a Banach space and  an absolutely continuous function, then the measure of the set
an absolutely continuous function, then the measure of the set  and
and  is zero.
is zero.
Using the previous results, we now prove two propositions that will be used later.
Proposition 2.19.
Let  and
and  the function defined by
the function defined by

Then, 
 -almost everywhere on
-almost everywhere on  .
.
Proof.
By Theorem 2.13, remark that

We can also check that for  right scattered,
right scattered,

Obviously,

It is well known that  almost everywhere on
almost everywhere on  . By Lemma 2.15, we have that
. By Lemma 2.15, we have that  except on a set
except on a set  such that
such that  . Since
. Since  is continuous, for
is continuous, for  right scattered,
right scattered,

by Theorem 2.2(ii). Then,  is
is  -differentiable at
-differentiable at  . By Proposition 2.12(ii),
. By Proposition 2.12(ii),  and, then, the proposition is proved.
and, then, the proposition is proved.
Proposition 2.20.
Let  be an absolutely continuous function, then the
be an absolutely continuous function, then the  -measure of the set
-measure of the set  and
and  is zero.
is zero.
Proof.
It suffices to consider the extension  of
of  on
on  and successively apply Theorem 2.16, Lemmas 2.18, 2.15, and the Proposition 2.12(ii).
and successively apply Theorem 2.16, Lemmas 2.18, 2.15, and the Proposition 2.12(ii).
We recall a notion of Sobolev's space of functions defined on a bounded time scale  where
where  . The definition and the result are from [14].
. The definition and the result are from [14].
Definition 2.21.
We say that a function  belongs to
belongs to  if and only if
if and only if  and there exists a function
and there exists a function  such that
such that  and
and

with

We say that a function  is in the set
is in the set  if each of its components
if each of its components  are in
are in  .
.
Theorem 2.22.
Suppose that  and that (2.22) holds for a function
and that (2.22) holds for a function  . Then, there exists a unique function
. Then, there exists a unique function  absolutely continuous such that
absolutely continuous such that  -almost everywhere on
-almost everywhere on  , one has
, one has  and
and  . Moreover, if
. Moreover, if  is
is  -continuous on
-continuous on  , then there exists a unique function
, then there exists a unique function  such that
such that  -almost everywhere on
-almost everywhere on  and such that
and such that  on
on  .
.
By the previous theorem, we can conclude that  is also continuous.
is also continuous.
Remark 2.23.
If , then its components
, then its components are in
are in . By Theorems 2.22 and 2.17,
. By Theorems 2.22 and 2.17, is
is - differentiable
- differentiable - a.e. on
- a.e. on . From Example 2.5, we obtain
. From Example 2.5, we obtain - a.e. on
- a.e. on .
.
We prove two maximum principles that will be useful to get a priori bounds for solutions of systems considered in this paper.
Lemma 2.24.
Let  such that
such that  -a.e.
-a.e.  . If one of the following conditions holds,
. If one of the following conditions holds,
-
(i)
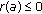 ,
, -
(ii)
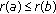 ,
,
then  , for every
, for every  .
.
Proof.
Suppose the conclusion is false. Then, there exists  such that
such that  , since
, since  is continuous on
is continuous on  . If
. If  , then
, then  exists, since
exists, since  and because
and because  . Then,
. Then,

which is a contradiction since  . If
. If  , then there exists an interval
, then there exists an interval  such that
such that  for all
for all  . Thus,
. Thus,

by hypothesis and by Theorem 2.17. Hence, we get a contradiction. The case  is impossible if hypothesis (i) holds and if
is impossible if hypothesis (i) holds and if  , we must have
, we must have  . If we take
. If we take  , by using previous steps of this proof, one can check that
, by using previous steps of this proof, one can check that  and, then, the lemma is proved.
and, then, the lemma is proved.
Lemma 2.25.
Let  be a function such that
be a function such that  -a.e. on
-a.e. on  if
if  , then
, then  , for every
, for every  .
.
Proof.
If there exists  such that
such that  , then there exists a
, then there exists a  such that
such that  . If
. If  and
and  , then
, then  . Since
. Since  ,
,  exists
exists  -almost everywhere. Then, we must have
-almost everywhere. Then, we must have

which contradicts the hypothesis of the lemma. If  and
and  , there exists an interval
, there exists an interval  such that
such that  for every
for every  . Then,
. Then,

by Theorem 2.17, which contradicts the fact that  is a maximum. If
is a maximum. If  , then by hypothesis, we must have
, then by hypothesis, we must have  . Thus, we can take
. Thus, we can take  , and by using the previous steps of this proof, one can check that
, and by using the previous steps of this proof, one can check that  . Then, the lemma is proved.
. Then, the lemma is proved.
Definition 2.26.
For  , the exponential function
, the exponential function may be defined as the unique solution of the initial value problem
may be defined as the unique solution of the initial value problem

More explicitly, the exponential function  is given by the formula
is given by the formula

where for  , we define
, we define  as
as

As direct consequences of Proposition 2.19 and Theorem 2.3, we get the following results.
Proposition 2.27.
If  , the function
, the function  defined by
defined by

is a solution of the problem

Proposition 2.28.
If  , then the function
, then the function  defined by
defined by

is a solution of the problem

Proposition 2.29.
If  , then the function
, then the function  defined by
defined by

is a solution of the problem

We now define a notion of Carathéodory functions on a compact time scale.
Definition 2.30.
A function  is called a
is called a  -Carathéodory function if the three following conditions hold.
-Carathéodory function if the three following conditions hold.
-
(C-i)The map
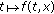 is
is  -measurable for every
-measurable for every 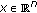 .
. -
(C-ii)The map
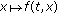 is continuous
is continuous 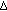 -a.e.
-a.e.  .
. -
(C-iii)For every
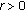 , there exists a function
, there exists a function 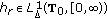 such that
such that  -a.e.
-a.e.  and for every
and for every 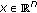 such that
such that 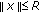 .
.
3. Existence Theorem for the Problem (1.1)
In this section, we establish an existence result for the problem (1.1). A solution of this problem will be a function  satisfying (1.1). Let us recall that
satisfying (1.1). Let us recall that  is compact and
is compact and  . We introduce the notion of solution tube for the problem (1.1).
. We introduce the notion of solution tube for the problem (1.1).
Definition 3.1.
Let  . We say that
. We say that  is a solution tube of (1.1) if
is a solution tube of (1.1) if
-
(i)

 -a.e.
-a.e.  and for every
and for every  such that
such that 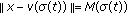 ,
, -
(ii)

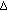 -a.e.
-a.e. 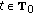 such that
such that 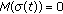 ,
, -
(iii)
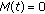 for every
for every  such that
such that 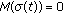 ,
, -
(iv)
If (BC) denotes (1.3),
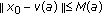 ; if (BC) denotes (1.4), then
; if (BC) denotes (1.4), then 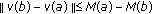 .
.
We denote

If  is a real interval
is a real interval  , our definition of solution tube is equivalent to the notion of solution tube introduced in [5].
, our definition of solution tube is equivalent to the notion of solution tube introduced in [5].
We consider the following problem.

where

Let us define the operator  by
by

Proposition 3.2.
If  is a solution tube of (1.1), (1.3), then
is a solution tube of (1.1), (1.3), then  is compact.
is compact.
Proof.
We first observe that from Definitions 2.30 and 3.1, there exists a function  such that
such that  -a.e.
-a.e.  for every
for every  .
.
Let  be a sequence of
be a sequence of  converging to
converging to  . By Proposition 2.9,
. By Proposition 2.9,

where  .
.
Then, we must show that the sequence  defined by
defined by

converges to the function  in
in  where
where

We can easily check that  for every
for every  and, then, by (C-ii) of Definition 2.30,
and, then, by (C-ii) of Definition 2.30,  -a.e.
-a.e.  . Using also the fact that
. Using also the fact that 
 -a.e.
-a.e.  , we deduce that
, we deduce that  in
in  by Theorem 2.10. This prove the continuity of
by Theorem 2.10. This prove the continuity of  .
.
For the second part of the proof, we have to show that the set  is relatively compact. Let
is relatively compact. Let  . Therefore,
. Therefore,

So,  is uniformly bounded. This set is also equicontinuous since for every
is uniformly bounded. This set is also equicontinuous since for every  ,
,

By an analogous version of the Arzelà-Ascoli Theorem adapted to our context,  is relatively compact. Hence,
is relatively compact. Hence,  is compact.
is compact.
We now define the operator  by
by

The following result can be proved as the previous one.
Proposition 3.3.
If  is a solution tube of (1.1), (1.4), then the operator
is a solution tube of (1.1), (1.4), then the operator  is compact.
is compact.
Now, we can obtain the main theorem of this section.
Theorem 3.4.
If  is a solution tube of (1.1), then the problem (1.1) has a solution
is a solution tube of (1.1), then the problem (1.1) has a solution  .
.
Proof.
By Proposition 3.2 (resp., Proposition 3.3),  (resp.,
(resp.,  ) is compact. It has a fixed point by the Schauder fixed-point Theorem. Proposition 2.27 (resp., Proposition 2.28) implies that this fixed point is a solution for the problem (3.2). Then, it suffices to show that for every solution
) is compact. It has a fixed point by the Schauder fixed-point Theorem. Proposition 2.27 (resp., Proposition 2.28) implies that this fixed point is a solution for the problem (3.2). Then, it suffices to show that for every solution  of (3.2),
of (3.2),  .
.
Consider the set  . By Remark 2.23,
. By Remark 2.23,  -a.e. on the set
-a.e. on the set  , we have
, we have

If  is right scattered, then
is right scattered, then  and
and

Therefore, since  is a solution tube of (1.1), we have
is a solution tube of (1.1), we have  -a.e. on
-a.e. on  that
that

On the other hand, we have  -a.e. on
-a.e. on  that
that

This last equality follows from Definition 3.1(iii) and Proposition 2.20.
If we set  , then
, then  -almost everywhere on
-almost everywhere on  . Moreover, since
. Moreover, since  is a solution tube of (1.1) and
is a solution tube of (1.1) and  satisfies (1.3) (resp.,
satisfies (1.3) (resp.,  satisfies (1.4)), then
satisfies (1.4)), then  (resp.,
(resp.,  ). Lemma 2.24 implies that
). Lemma 2.24 implies that  . Therefore,
. Therefore,  and, hence, the theorem is proved.
and, hence, the theorem is proved.
Existence theorems are obtained in [7] for the problem (1.1), (1.3) when  is continuous by using a hypothesis different of ours. When
is continuous by using a hypothesis different of ours. When  is bounded, we can directly use the Schauder fixed-point Theorem to deduce the existence of a solution to (1.1), (1.3). We now show that in the case where
is bounded, we can directly use the Schauder fixed-point Theorem to deduce the existence of a solution to (1.1), (1.3). We now show that in the case where  is unbounded, Theorems 4.7 and 4.8 of [7] become corollaries of our existence theorem.
is unbounded, Theorems 4.7 and 4.8 of [7] become corollaries of our existence theorem.
Corollary 3.5.
Let  be an unbounded continuous function. If there exist non-negative constants
be an unbounded continuous function. If there exist non-negative constants  and
and  such that
such that

for every  and every
and every  , then the problem (1.1), (1.3) has at least one solution.
, then the problem (1.1), (1.3) has at least one solution.
Proof.
Observe that  since
since  is unbounded. By hypothesis, there exists a constant
is unbounded. By hypothesis, there exists a constant  such that
such that  . Let us define
. Let us define  by
by

Then,  for every
for every  and, thus,
and, thus,

for every  and every
and every  . Then, if we take
. Then, if we take  , we get a solution tube
, we get a solution tube  for our problem and by Theorem 3.4, the problem has a solution
for our problem and by Theorem 3.4, the problem has a solution  such that
such that  for every
for every  .
.
Corollary 3.6.
Let  be an unbounded continuous function. If there exists a nonnegative constant
be an unbounded continuous function. If there exists a nonnegative constant  such that
such that

for every  and every
and every  , then the problem (1.1), (1.3) has at least one solution.
, then the problem (1.1), (1.3) has at least one solution.
4. Existence Theorem for the Problem (1.2)
In this section, we establish an existence result for the problem (1.2). A solution of this problem will be a function  for which (1.2) is satisfied. As before,
for which (1.2) is satisfied. As before,  is compact and
is compact and  . We introduce the notion of solution tube for the problem (1.2). Conditions of this definition are slightly different than conditions in Definition 3.1.
. We introduce the notion of solution tube for the problem (1.2). Conditions of this definition are slightly different than conditions in Definition 3.1.
Definition 4.1.
Let  . We say that
. We say that  is a solution tube of (1.2) if
is a solution tube of (1.2) if
-
(i)
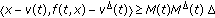 -a.e.
-a.e. 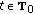 and for every
and for every 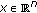 such that
such that  ,
, -
(ii)
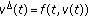 and
and  ,
,  -a.e.
-a.e. 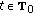 such that
such that 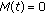 ,
, -
(iii)
 .
.
We consider the following problem.

where  is defined in (3.3).
is defined in (3.3).
Let us define the operator  by
by

The following result can be proved as Proposition 3.2.
Proposition 4.2.
If  is a solution tube of (1.2), then the operator
is a solution tube of (1.2), then the operator  is compact.
is compact.
Here is the main existence theorem for problem (1.2).
Theorem 4.3.
If  is a solution tube of (1.2), then the problem (1.2) has a solution
is a solution tube of (1.2), then the problem (1.2) has a solution  .
.
Proof.
By Proposition 4.2,  is compact. Then, by the Schauder fixed-point Theorem,
is compact. Then, by the Schauder fixed-point Theorem,  has a fixed point which is a solution of (4.1) by Proposition 2.29. It suffices to show that for every solution
has a fixed point which is a solution of (4.1) by Proposition 2.29. It suffices to show that for every solution  of (4.1),
of (4.1),  .
.
Let us consider the set  . By Remark 2.23,
. By Remark 2.23,  -a.e. on the set
-a.e. on the set  we have
we have

If  is right scattered, then
is right scattered, then  and
and

Since  is a solution tube of (1.2), we have
is a solution tube of (1.2), we have  -a.e. on
-a.e. on  that
that

On the other hand, we have  -a.e. on
-a.e. on  that
that

If we set  , then
, then  -almost everywhere on
-almost everywhere on  . Moreover, since
. Moreover, since  is a solution tube of (1.2) and
is a solution tube of (1.2) and  satisfies (1.4),
satisfies (1.4),  . Lemma 2.25 implies that
. Lemma 2.25 implies that  . So,
. So,  and the theorem is proved.
and the theorem is proved.
Let us observe that the following results obtained in [6] and [15], respectively, are different from ours.
Theorem 4.4.
Let  be a continuous function with
be a continuous function with  such that
such that  . If there exist nonnegative constants
. If there exist nonnegative constants  and
and  such that
such that

for every  , where
, where  is defined by
is defined by  with
with

then the problem (1.2) has a solution.
Theorem 4.5.
Let  ,
,  and
and  a continuous function. If there exist nonnegative constants
a continuous function. If there exist nonnegative constants  and
and  such that
such that

for every  , then the difference equation (1.2) has one solution.
, then the difference equation (1.2) has one solution.
Observe that Theorem 4.3 is valid for every arbitrary time scale  . Here is an example where (4.7) and (4.9) are not satisfied, but where Theorem 4.3 can be applied to deduce the existence of a solution.
. Here is an example where (4.7) and (4.9) are not satisfied, but where Theorem 4.3 can be applied to deduce the existence of a solution.
Example 4.6.
Consider the system

where  are real positive constants such that
are real positive constants such that  and where
and where  is a continuous function such that
is a continuous function such that  for every
for every  .
.
We first show that this system do not satisfy (4.7). Suppose there exist non-negative constants  and
and  such that
such that

for every  .
.
If we define  , then
, then

for every  .
.
Then,

for every  , where
, where  ,
,  ,
,  , and
, and  . Taking the limit as
. Taking the limit as  , we get a contradiction. Similarly, if
, we get a contradiction. Similarly, if  , it can be shown that (4.9) is not satisfied. On the other hand, it is easy to verify that
, it can be shown that (4.9) is not satisfied. On the other hand, it is easy to verify that  is a solution tube of (4.10). By Theorem 4.3, this problem has a solution
is a solution tube of (4.10). By Theorem 4.3, this problem has a solution  such that
such that  for every
for every  .
.
Definition 4.1 generalizes the notions of lower and upper solutions  and
and  introduced in [3] in the particular case where the problem (1.2) is considered with
introduced in [3] in the particular case where the problem (1.2) is considered with  ,
,  for some
for some  and with
and with  depending only on
depending only on  . We recall these definitions. Consider the problem
. We recall these definitions. Consider the problem

where  .
.
Definition 4.7.
A vector  (resp.,
(resp.,  ) is called an upper solution (resp., a lower solution) of (4.14) if
) is called an upper solution (resp., a lower solution) of (4.14) if
-
(i)
for every
 ,
,  (resp.,
(resp., 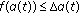 ),
), -
(ii)
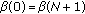 (resp.,
(resp., 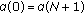 ).
).
Remark that if  are, respectively, lower and upper solutions of (4.14) such that
are, respectively, lower and upper solutions of (4.14) such that  for every
for every  , then
, then  is a solution tube for this problem. Conversely, if
is a solution tube for this problem. Conversely, if  is a solution tube of (4.14), then
is a solution tube of (4.14), then  and
and  are, respectively, lower and upper solution for the same problem if, in addition, condition (ii) of Definition 4.7 is satisfied. Then, Theorem 5 of [3] becomes a corollary of Theorem 4.3.
are, respectively, lower and upper solution for the same problem if, in addition, condition (ii) of Definition 4.7 is satisfied. Then, Theorem 5 of [3] becomes a corollary of Theorem 4.3.
Corollary 4.8.
If  are, respectively, lower and upper solutions of (4.14) such that
are, respectively, lower and upper solutions of (4.14) such that  for every
for every  , then this equation has a solution
, then this equation has a solution  such that
such that  for every
for every  .
.
References
Otero-Espinar V, Vivero DR: Existence of extremal solutions by approximation to a first-order initial dynamic equation with Carathéodory's conditions and discontinuous non-linearities. Journal of Difference Equations and Applications 2006,12(12):1225-1241. 10.1080/10236190600949808
Otero-Espinar V, Vivero DR: The existence and approximation of extremal solutions to several first-order discontinuous dynamic equations with nonlinear boundary value conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,68(7):2027-2037. 10.1016/j.na.2007.01.030
Bereanu C, Mawhin J: Existence and multiplicity results for periodic solutions of nonlinear difference equations. Journal of Difference Equations and Applications 2006,12(7):677-695. 10.1080/10236190600654689
Franco D, O'Regan D, Perán J: Upper and lower solution theory for first and second order difference equations. Dynamic Systems and Applications 2004,13(2):273-282.
Mirandette B: Résultats d'Existence pour des Systèmes d'Équations Différentielles du Premier Ordre avec Tube-Solution. Mémoire de Maîtrise, Université de Montréal, Montréal, Canada; 1996.
Dai Q, Tisdell CC: Existence of solutions to first-order dynamic boundary value problems. International Journal of Difference Equations 2006,1(1):1-17.
Tisdell CC, Zaidi A: Basic qualitative and quantitative results for solutions to nonlinear, dynamic equations on time scales with an application to economic modelling. Nonlinear Analysis: Theory, Methods & Applications 2008,68(11):3504-3524. 10.1016/j.na.2007.03.043
Otero-Espinar V, Vivero DR: Existence and approximation of extremal solutions to first-order infinite systems of functional dynamic equations. Journal of Mathematical Analysis and Applications 2008,339(1):590-597. 10.1016/j.jmaa.2007.06.031
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Bohner M, Peterson A: Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics. Resultate der Mathematik 1990,18(1-2):18-56.
Cabada A, Vivero DR:Expression of the Lebesgue
 -integral on time scales as a usual Lebesgue integral: application to the calculus of
-integral on time scales as a usual Lebesgue integral: application to the calculus of 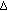 -antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028
-antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028Cabada A, Vivero DR: Criterions for absolute continuity on time scales. Journal of Difference Equations and Applications 2005,11(11):1013-1028. 10.1080/10236190500272830
Agarwal RP, Otero-Espinar V, Perera K, Vivero DR: Basic properties of Sobolev's spaces on time scales. Advances in Difference Equations 2006, 2006:-14.
Tisdell CC: On first-order discrete boundary value problems. Journal of Difference Equations and Applications 2006,12(12):1213-1223. 10.1080/10236190600949790
Acknowledgment
The author would like to thank Professor Marlene Frigon for useful discussion and comments and the FQRNT for financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gilbert, H. Existence Theorems for First-Order Equations on Time Scales with  -Carathéodory Functions.
Adv Differ Equ 2010, 650827 (2010). https://doi.org/10.1155/2010/650827
-Carathéodory Functions.
Adv Differ Equ 2010, 650827 (2010). https://doi.org/10.1155/2010/650827
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/650827
 is
is  -differentiable at
-differentiable at 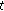 , then
, then 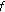 is continuous at
is continuous at 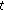 .
.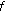 is continuous at
is continuous at 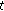 and if
and if 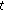 is right-scattered, then
is right-scattered, then 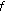 is
is 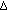 -differentiable at
-differentiable at 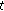 and
and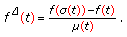
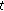 is right dense, then
is right dense, then 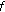 is
is 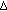 -differentiable at
-differentiable at  if and only if
if and only if 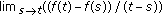 exists in
exists in 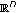 . In this case,
. In this case, 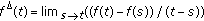 .
.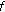 is
is 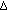 -differentiable at
-differentiable at  , then
, then 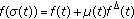 .
.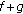 is
is 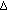 -differentiable at
-differentiable at 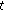 and
and 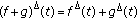 ,
, is
is 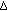 -differentiable at
-differentiable at  for every
for every 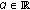 and
and 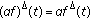 ,
,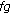 is
is 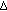 -differentiable at
-differentiable at  and
and 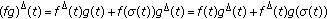 ,
,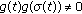 , then
, then 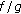 is
is  -differentiable at
-differentiable at 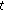 and
and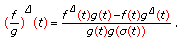
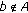 , then
, then
 if and only if
if and only if  and A has no right-scattered points. Here,
and A has no right-scattered points. Here,  .
.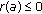 ,
,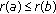 ,
,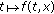 is
is  -measurable for every
-measurable for every 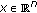 .
.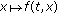 is continuous
is continuous 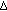 -a.e.
-a.e.  .
.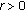 , there exists a function
, there exists a function 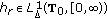 such that
such that  -a.e.
-a.e.  and for every
and for every 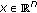 such that
such that 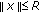 .
.
 -a.e.
-a.e.  and for every
and for every  such that
such that 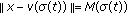 ,
,
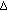 -a.e.
-a.e. 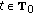 such that
such that 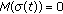 ,
,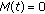 for every
for every  such that
such that 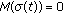 ,
,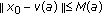 ; if (BC) denotes (1.4), then
; if (BC) denotes (1.4), then 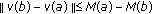 .
.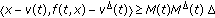 -a.e.
-a.e. 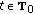 and for every
and for every 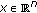 such that
such that  ,
,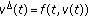 and
and  ,
,  -a.e.
-a.e. 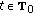 such that
such that 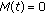 ,
, .
. ,
,  (resp.,
(resp., 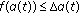 ),
),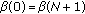 (resp.,
(resp., 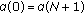 ).
). -integral on time scales as a usual Lebesgue integral: application to the calculus of
-integral on time scales as a usual Lebesgue integral: application to the calculus of  -antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028
-antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028