- Research Article
- Open access
- Published:
Error Bounds for Asymptotic Solutions of Second-Order Linear Difference Equations II: The First Case
Advances in Difference Equations volume 2010, Article number: 594783 (2010)
Abstract
We discuss in detail the error bounds for asymptotic solutions of second-order linear difference equation  where
where  and
and  are integers,
are integers,  and
and  have asymptotic expansions of the form
have asymptotic expansions of the form  ,
,  , for large values of
, for large values of  ,
,  , and
, and  .
.
1. Introduction
Asymptotic expansion of solutions to second-order linear difference equations is an old subject. The earliest work as we know can go back to 1911 when Birkhoff [1] first deal with this problem. More than eighty years later, this problem was picked up again by Wong and Li [2, 3]. This time two papers on asymptotic solutions to the following difference equations:


were published, respectively, where coefficients  and
and  have asymptotic properties
have asymptotic properties

for large values of  ,
,  ,
, 
 , and
, and  .
.
Unlike the method used by Olver [4] to treat asymptotic solutions of second-order linear differential equations, the method used in Wong and Li's papers cannot give us way to obtain error bounds of these asymptotic solutions. Only order estimations were given in their papers. The estimations of error bounds for these asymptotic solutions to (1.1) were given in [5] by Zhang et al. But the problem of obtaining error bounds for these asymptotic solutions to (1.2) is still open. The purpose of this and the next paper (Error bounds for asymptotic solutions of second-order linear difference equations II: the second case) is to estimate error bounds for solutions to (1.2). The idea used in this paper is similar to that of Olver to obtain error bounds to the Liouville-Green (WKB) asymptotic expansion of solutions to second-order differential equations. It should be pointed out that similar method appeared in some early papers, such as Spigler and Vianello's papers [6–9].
In Wong and Li's second paper [3], two different cases were given according to different values of parameters. The first case is devoted to the situation when  , and in the second case as
, and in the second case as  where
where  . The whole proof of the result is too long to understand, so we divide the estimations into two parts, part I (this paper) and part II (the next paper), which correspond to the different two cases of [3], respectively.
. The whole proof of the result is too long to understand, so we divide the estimations into two parts, part I (this paper) and part II (the next paper), which correspond to the different two cases of [3], respectively.
In the rest of this section, we introduce the main results of [3] in the case that  is positive. In the next section, we give two lemmas on estimations of bounds for solutions to a special summation equation and a first order nonlinear difference equation which will be often used later. Section 3 is devoted to the case when
is positive. In the next section, we give two lemmas on estimations of bounds for solutions to a special summation equation and a first order nonlinear difference equation which will be often used later. Section 3 is devoted to the case when  . And in Section 4, we discuss the case when
. And in Section 4, we discuss the case when  . The next paper (Error bounds for asymptotic solutions of second-order linear difference equations II: the second case) is dedicated to the case when
. The next paper (Error bounds for asymptotic solutions of second-order linear difference equations II: the second case) is dedicated to the case when  .
.
1.1. The Result in [3] When 
When  , from [3] we know that (1.2) has two linearly independent solution
, from [3] we know that (1.2) has two linearly independent solution  and
and 




for  .
.
1.2. The Result in [3] When 
When  , from [3] we know that (1.2) has two linearly independent solutions
, from [3] we know that (1.2) has two linearly independent solutions  and
and 




In the following sections, we will discuss in detail the error bounds of the proceeding asymptotic solutions of (1.2). Before discussing the error bounds, we consider some lemmas.
2. Lemmas
2.1. The Bounds for Solutions to the Summation Equation
We consider firstly a bound of a special solution for the "summary equation"

Lemma 2.1.
Let  ,
,  ,
,  ,
,  be real or complex functions of integer variables
be real or complex functions of integer variables  ;
;  and
and  are integers. If there exist nonnegative constants
are integers. If there exist nonnegative constants  ,
,  ,
,  ,
,  ,
,  ,
,  , β,
, β,  ,
,  ,
,  ,
,  ,
,  ,
,  which satisfy
which satisfy

and when  ,
,

where  and
and  are positive functions of integer variable
are positive functions of integer variable  . Let
. Let  ,
,  be integers defined by
be integers defined by

then (2.1) has a solution  , which satisfies
, which satisfies

for  .
.
Proof.
Set

then

The inequality  , is used here. Assuming that
, is used here. Assuming that

where

then

By induction, the inequality holds for any integer  . Hence the series
. Hence the series

when  , that is,
, that is,  , is uniformly convergent in
, is uniformly convergent in  where
where

And its sum

satisfies

So we get the bound of any solution for the "summary equation" (2.1). Next we consider a nonlinear first-order difference equation.
2.2. The Bound Estimate of a Solution to a Nonlinear First-Order Difference Equation
Lemma 2.2.
If the function  satisfies
satisfies

where  (
( and
and  are constants), when
are constants), when  is large enough, then the following first-order difference equation
is large enough, then the following first-order difference equation

has a solution  such that
such that  is bounded by a constant
is bounded by a constant  , when
, when  is big enough.
is big enough.
Proof.
Obviously from the conditions of this lemma, we know that infinite products  and
and  are convergent.
are convergent.

is a solution of (2.16) with the infinite condition. Let  ; then when
; then when  is large enough,
is large enough,

3. Error Bounds in the Case When 
Before giving the estimations of error bounds of solutions to (1.2), we rewrite  as
as

with

and  ,
,  , being error terms. Then
, being error terms. Then  ,
,  , satisfy inhomogeneous second-order linear difference equations
, satisfy inhomogeneous second-order linear difference equations

where

We know from [3] that

3.1. The Error Bound for the Asymptotic Expansion of 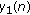
Now we firstly estimate the error bound of the asymptotic expansion of  in the case
in the case  . Let
. Let

It can be easily verified that

are two linear independent solutions of the comparative difference equation

From the definition, we know that the two-term approximation of  is
is

where  is the reminder and the coefficient of
is the reminder and the coefficient of  is zero. So
is zero. So  is a constant. And
is a constant. And  satisfies
satisfies  being a constant; here we have made use of the definitions of
being a constant; here we have made use of the definitions of  in (1.5), (1.7), and
in (1.5), (1.7), and  .
.
Equation (3.8) is a second-order linear difference equation with two known linear independent solutions. Its coefficients are quite similar to those in (3.3). This reminds us to rewrite (3.3) in the form similar to (3.8).
According to the coefficients in (3.8), we rewrite (3.3) as

where  and
and  are such that
are such that

are finite. Equation (3.10) is a inhomogeneous second-order linear difference equation; its solution takes the form of a particular solution added to an arbitrary linear combination of solutions to the associated homogeneous linear difference equation(3.8).
From [10], any solution of the "summary equation"

is a solution of (3.10), where

Now we estimate the bound of the function  .
.
Firstly we consider the denominator in  . We get from(3.8)
. We get from(3.8)

Set the Wronskian of the two solutions of the comparative difference equation as

we have

From (3.16), we have

From Lemma 3 of [5], we obtain

where


 is an integer which is large enough such that
is an integer which is large enough such that  , when
, when  .
.
Let  , for the property of
, for the property of  , we know that
, we know that  is a constant. Then we obtain from (3.18)
is a constant. Then we obtain from (3.18)

Now considering the numerator in  , we get
, we get

Here we have made use of  .
.
From Lemma 2 of [5], we have

where  is a constant. For the bound of
is a constant. For the bound of  , we set
, we set

then

where

By simple calculations, we get

Here we have made use of (1.5) and (1.7).
Since  , we have
, we have

Here we also have made use of (1.5) and (1.7).
Let

we have from (3.24) the bound of 

For the bound of  , set
, set  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ; we have from Lemma 2.1 that
; we have from Lemma 2.1 that

when

that is,  and
and  .
.
3.2. The Error Bound for the Asymptotic Expansion of  (
( )
)
Now we estimate the error bound of the asymptotic expansion of the linear independent solution  to the original difference equation as
to the original difference equation as  . Let
. Let

From (3.3), we have

For  being a solution of (1.2), let
being a solution of (1.2), let

then  satisfies the first-order linear difference equation
satisfies the first-order linear difference equation

The solution of (3.36) is

where  is a constant, and
is a constant, and  is an integer which is large enough such that when
is an integer which is large enough such that when  ,
,

The two-term approximation of  is
is

where  is the reminder and
is the reminder and  is a constant.
is a constant.
From Lemma 3 of [5], we obtain

where

are constants.
Substituting (3.38) and (3.40) into (3.37), we get

Let  then
then

From (3.35), we have

where  is a constant. Let
is a constant. Let  ; we have
; we have

For  , there exists a positive integer
, there exists a positive integer  such that
such that

when  . Thus the sequence
. Thus the sequence  is increasing when
is increasing when  .
.
Let  ; then
; then

where  Hence
Hence

From (3.33), we obtain

Thus we complete the estimate of error bounds to asymptotic expansions of solutions of (1.2) as  .
.
4. Error Bounds in Case When 
Here we also rewrite  as
as

with

and  ,
,  ,2, are error terms. Then
,2, are error terms. Then  ,
,  ,2, satisfy the inhomogeneous second-order linear difference equations
,2, satisfy the inhomogeneous second-order linear difference equations

where

We know from [3] that

4.1. The Error Bound for the Asymptotic Expansion of 
Now let us come to the case when  . This time a difference equation which has two known linear independent solutions is also constructed for the purpose of comparison for (1.2).
. This time a difference equation which has two known linear independent solutions is also constructed for the purpose of comparison for (1.2).
Since

where

is a constant and  (
( is a constant), from Lemma 2.2, we know the difference equation
is a constant), from Lemma 2.2, we know the difference equation

with condition  having a solution
having a solution  such that
such that

is a constant. And the function

such that

is a constant. Here we have made use of the definitions of  ,
,  ,
,  ,
,  in (1.9), (1.11) and
in (1.9), (1.11) and  .
.
Obviously functions

are two linear independent solutions of the difference equation

This difference equation(4.13) can be regarded as the comparative equation of (4.3). Rewriting (4.3) in the form similar to the comparative difference equation (4.13), we get

where  has the property that
has the property that  is a constant. Equation (4.14) is an inhomogeneous second-order linear difference equation; its solution takes the form of a particular solution added to an arbitrary linear combination of solutions to the associated homogeneous linear difference equation (4.13).
is a constant. Equation (4.14) is an inhomogeneous second-order linear difference equation; its solution takes the form of a particular solution added to an arbitrary linear combination of solutions to the associated homogeneous linear difference equation (4.13).
From [10], any solution of the "summary equation"

where

is a solution of (4.14).
Similar to Section 3.1, we have

Let

we get

Set  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ; we have from Lemma 2.1 that
; we have from Lemma 2.1 that

when

that is,
 ,
,  .
.
4.2. The Error Bound for the Asymptotic Expansion of 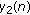
Let

From (3.3), we have

Using the method employed in Section 3.2, it is not difficult to obtain

Now we completed the estimate of the error bounds for asymptotic solutions to second order linear difference equations in the first case. For the second case, we leave it to the second part of this paper: Error Bound for Asymptotic Solutions of Second-order Linear Difference Equation II: the second case.
In the rest of this paper, we would like to give an example to show how to use the results of this paper to obtain error bounds of asymptotic solutons to second-order linear difference equations. Here the difference equation is

It is a special case of the equation

 , which is satisfied by Tricomi-Carlitz polynomials. By calculation, the constant
, which is satisfied by Tricomi-Carlitz polynomials. By calculation, the constant  in (3.30) is
in (3.30) is  . So (4.25) has a solution
. So (4.25) has a solution

for  with the error term
with the error term  satisfing
satisfing

References
Birkhoff GD: General theory of linear difference equations. Transactions of the American Mathematical Society 1911,12(2):243-284. 10.1090/S0002-9947-1911-1500888-5
Wong R, Li H: Asymptotic expansions for second-order linear difference equations. Journal of Computational and Applied Mathematics 1992,41(1-2):65-94. 10.1016/0377-0427(92)90239-T
Wong R, Li H: Asymptotic expansions for second-order linear difference equations. II. Studies in Applied Mathematics 1992,87(4):289-324.
Olver FWJ: Asymptotics and Special Functions, Computer Science and Applied Mathematics. Academic Press, New York, NY, USA; 1974:xvi+572.
Zhang JM, Li XC, Qu CK: Error bounds for asymptotic solutions of second-order linear difference equations. Journal of Computational and Applied Mathematics 1996,71(2):191-212. 10.1016/0377-0427(95)00218-9
Spigler R, Vianello M: Liouville-Green approximations for a class of linear oscillatory difference equations of the second order. Journal of Computational and Applied Mathematics 1992,41(1-2):105-116. 10.1016/0377-0427(92)90241-O
Spigler R, Vianello M:WKBJ-type approximation for finite moments perturbations of the differential equation
 and the analogous difference equation. Journal of Mathematical Analysis and Applications 1992,169(2):437-452. 10.1016/0022-247X(92)90089-V
and the analogous difference equation. Journal of Mathematical Analysis and Applications 1992,169(2):437-452. 10.1016/0022-247X(92)90089-VSpigler R, Vianello M: Discrete and continuous Liouville-Green-Olver approximations: a unified treatment via Volterra-Stieltjes integral equations. SIAM Journal on Mathematical Analysis 1994,25(2):720-732. 10.1137/S0036141092231215
Spigler R, Vianello M: A survey on the Liouville-Green (WKB) approximation for linear difference equations of the second order. In Advances in Difference Equations (Veszprém, 1995). Edited by: Elaydi N, Györi I, Ladas G. Gordon and Breach, Amsterdam, The Netherlands; 1997:567-577.
Bender CM, Orszag SA: Advanced Mathematical Methods for Scientists and Engineers, International Series in Pure and Applied Mathematics. McGraw-Hill Book, New York, NY, USA; 1978:xiv+593.
Acknowledgments
The authors would like to thank Dr. Z. Wang for his helpful discussions and suggestions. The second author thanks Liu Bie Ju Center for Mathematical Science and Department of Mathematics of City University of Hong Kong for their hospitality. This work is partially supported by the National Natural Science Foundation of China (Grant no. 10571121 and Grant no. 10471072) and Natural Science Foundation of Guangdong Province (Grant no. 5010509).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cao, L., Zhang, J. Error Bounds for Asymptotic Solutions of Second-Order Linear Difference Equations II: The First Case. Adv Differ Equ 2010, 594783 (2010). https://doi.org/10.1155/2010/594783
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/594783



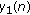
 (
( )
)

 and the analogous difference equation. Journal of Mathematical Analysis and Applications 1992,169(2):437-452. 10.1016/0022-247X(92)90089-V
and the analogous difference equation. Journal of Mathematical Analysis and Applications 1992,169(2):437-452. 10.1016/0022-247X(92)90089-V