- Research Article
- Open access
- Published:
Boundary Value Problems for Delay Differential Systems
Advances in Difference Equations volume 2010, Article number: 593834 (2010)
Abstract
Conditions are derived of the existence of solutions of linear Fredholm's boundary-value problems for systems of ordinary differential equations with constant coefficients and a single delay, assuming that these solutions satisfy the initial and boundary conditions. Utilizing a delayed matrix exponential and a method of pseudoinverse by Moore-Penrose matrices led to an explicit and analytical form of a criterion for the existence of solutions in a relevant space and, moreover, to the construction of a family of linearly independent solutions of such problems in a general case with the number of boundary conditions (defined by a linear vector functional) not coinciding with the number of unknowns of a differential system with a single delay. As an example of application of the results derived, the problem of bifurcation of solutions of boundary-value problems for systems of ordinary differential equations with a small parameter and with a finite number of measurable delays of argument is considered.
1. Introduction
First we mention auxiliary results regarding the theory of differential equations with delay. Consider a system of linear differential equations with concentrated delay

assuming that

where  is an
is an  real matrix, and
real matrix, and  is an
is an  -dimensional real column vector, with components in the space
-dimensional real column vector, with components in the space  (where
(where  ) of functions integrable on
) of functions integrable on  with the degree
with the degree  ; the delay
; the delay  is a function
is a function  measurable on
measurable on  ;
;  is a given vector function with components in
is a given vector function with components in  . Using the denotations
. Using the denotations


where  is an
is an  -dimensional zero column vector, and assuming
-dimensional zero column vector, and assuming  , it is possible to rewrite (1.1), (1.2) as
, it is possible to rewrite (1.1), (1.2) as

where  is an
is an  -dimensional column vector defined by the formula
-dimensional column vector defined by the formula

We will investigate (1.5) assuming that the operator  maps a Banach space
maps a Banach space  of absolutely continuous functions
of absolutely continuous functions  into a Banach space
into a Banach space 
 of function
of function  integrable on
integrable on  with the degree
with the degree  ; the operator
; the operator  maps the space
maps the space  into the space
into the space  . Transformations of (1.3), (1.4) make it possible to add the initial vector function
. Transformations of (1.3), (1.4) make it possible to add the initial vector function  ,
,  to nonhomogeneity, thus generating an additive and homogeneous operation not depending on
to nonhomogeneity, thus generating an additive and homogeneous operation not depending on  , and without the classical assumption regarding the continuous connection of solution
, and without the classical assumption regarding the continuous connection of solution  with the initial function
with the initial function  at
at  .
.
A solution of differential system (1.5) is defined as an  -dimensional column vector function
-dimensional column vector function  , absolutely continuous on
, absolutely continuous on  with a derivative
with a derivative  in a Banach space
in a Banach space 
 of functions integrable on
of functions integrable on  with the degree
with the degree  satisfying (1.5) almost everywhere on
satisfying (1.5) almost everywhere on  . Throughout this paper we understand the notion of a solution of a differential system and the corresponding boundary value problem in the sense of the above definition.
. Throughout this paper we understand the notion of a solution of a differential system and the corresponding boundary value problem in the sense of the above definition.
Such treatment makes it possible to apply the well-developed methods of linear functional analysis to (1.5) with a linear and bounded operator  . It is well known (see, e.g., [1–4]) that a nonhomogeneous operator equation (1.5) with delayed argument is solvable in the space
. It is well known (see, e.g., [1–4]) that a nonhomogeneous operator equation (1.5) with delayed argument is solvable in the space  for an arbitrary right-hand side
for an arbitrary right-hand side  and has an
and has an  -dimensional family of solutions
-dimensional family of solutions  in the form
in the form

where the kernel  is an
is an  Cauchy matrix defined in the square
Cauchy matrix defined in the square  which is, for every
which is, for every  a solution of the matrix Cauchy problem:
a solution of the matrix Cauchy problem:

where  if
if  , and
, and  is the
is the  null matrix. A fundamental
null matrix. A fundamental  matrix
matrix  for the homogeneous
for the homogeneous  (1.5) has the form
(1.5) has the form  ,
,  .
.
A serious disadvantage of this approach, when investigating the above-formulated problem, is the necessity to find the Cauchy matrix  [5, 6]. It exists but, as a rule, can only be found numerically. Therefore, it is important to find systems of differential equations with delay such that this problem can be solved directly. Below, we consider the case of a system with what is called a single delay [7]. In this case, the problem of how to construct the Cauchy matrix is solved analytically thanks to a delayed matrix exponential, as defined below.
[5, 6]. It exists but, as a rule, can only be found numerically. Therefore, it is important to find systems of differential equations with delay such that this problem can be solved directly. Below, we consider the case of a system with what is called a single delay [7]. In this case, the problem of how to construct the Cauchy matrix is solved analytically thanks to a delayed matrix exponential, as defined below.
2. A Delayed Matrix Exponential
Consider a Cauchy problem for a linear nonhomogeneous differential system with constant coefficients and with a single delay 


with  constant matrix
constant matrix  ,
,  ,
,  ,
,  and an unknown vector solution
and an unknown vector solution  . Together with a nonhomogeneous problem (2.1), (2.2), we consider a related homogeneous problem
. Together with a nonhomogeneous problem (2.1), (2.2), we consider a related homogeneous problem


Denote by  a matrix function called a delayed matrix exponential (see [7]) and defined as
a matrix function called a delayed matrix exponential (see [7]) and defined as

This definition can be reduced to the following expression:

where  is the greatest integer function. The delayed matrix exponential equals a unit matrix
is the greatest integer function. The delayed matrix exponential equals a unit matrix  on
on  and represents a fundamental matrix of a homogeneous system with a single delay.
and represents a fundamental matrix of a homogeneous system with a single delay.
We mention some of the properties of  given in [7]. Regarding the system without delay
given in [7]. Regarding the system without delay  , the delayed matrix exponential does not have the form of a matrix series, but it is a matrix polynomial, depending on the time interval in which it is considered. It is easy to prove directly that the delayed matrix exponential
, the delayed matrix exponential does not have the form of a matrix series, but it is a matrix polynomial, depending on the time interval in which it is considered. It is easy to prove directly that the delayed matrix exponential  satisfies the relations
satisfies the relations

By integrating the delayed matrix exponential, we get

where  . If, moreover, the matrix
. If, moreover, the matrix  is regular, then
is regular, then

Delayed matrix exponential  ,
,  is an infinitely many times continuously differentiable function except for the nodes
is an infinitely many times continuously differentiable function except for the nodes  ,
,  where there is a discontinuity of the derivative of order
where there is a discontinuity of the derivative of order  :
:

The following results (proved in [7] and being a consequence of (1.7) with  as well) hold.
as well) hold.
Theorem 2.1.
-
(A)
The solution of a homogeneous system (2.3) with a single delay satisfying the initial condition (2.4) where
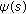 is an arbitrary continuously differentiable vector function can be represented in the form
is an arbitrary continuously differentiable vector function can be represented in the form 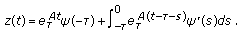 (2.11)
(2.11)
-
(B)
A particular solution of a nonhomogeneous system (2.1) with a single delay satisfying the zero initial condition
 if
if 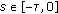 can be represented in the form
can be represented in the form 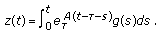 (2.12)
(2.12)
-
(C)
A solution of a Cauchy problem of a nonhomogeneous system with a single delay (2.1) satisfying a constant initial condition
 (2.13)
(2.13)
has the form

3. Main Results
Without loss of generality, let  . The problem (2.1), (2.2) can be transformed
. The problem (2.1), (2.2) can be transformed  to an equation of type (1.1) (see (1.5)):
to an equation of type (1.1) (see (1.5)):

where, in accordance with (1.3), (1.4),

A general solution of a Cauchy problem for a nonhomogeneous system (3.1) with a single delay satisfying a constant initial condition

has the form (1.7):

where, as can easily be verified (in view of the above-defined delayed matrix exponential) by substituting into (3.1),

is a normal fundamental matrix of the homogeneous system related to (3.1) (or (2.1)) with the initial data  , and the Cauchy matrix
, and the Cauchy matrix  has the form
has the form

Obviously,

and, therefore, the initial problem (3.1) for systems of ordinary differential equations with constant coefficients and a single delay, satisfying a constant initial condition, has an  -parametric family of linearly independent solutions
-parametric family of linearly independent solutions

Now we will consider a general Fredholm boundary value problem for system (3.1).
3.1. Fredholm Boundary Value Problem
Using the results in [8, 9], it is easy to derive statements for a general boundary value problem if the number  of boundary conditions does not coincide with the number
of boundary conditions does not coincide with the number  of unknowns in a differential system with a single delay.
of unknowns in a differential system with a single delay.
We consider a boundary value problem

assuming that

or, using (3.2), in an equivalent form


where  is an
is an  -dimensional constant vector column, and
-dimensional constant vector column, and  is a linear vector functional. It is well known that, for functional differential equations, such problems are of Fredholm's type (see, e.g., [1, 9]). We will derive the necessary and sufficient conditions and a representation (in an explicit analytical form) of the solutions
is a linear vector functional. It is well known that, for functional differential equations, such problems are of Fredholm's type (see, e.g., [1, 9]). We will derive the necessary and sufficient conditions and a representation (in an explicit analytical form) of the solutions  of the boundary value problem (3.11), (3.12).
of the boundary value problem (3.11), (3.12).
We recall that, because of properties (3.6)–(3.7), a general solution of system (3.11) has the form

In the algebraic system

derived by substituting (3.13) into boundary condition (3.12); the constant matrix

has a size of  . Denote
. Denote

where, obviously,  . Adopting the well-known notation (e.g., [9]), we define an
. Adopting the well-known notation (e.g., [9]), we define an  -dimensional matrix
-dimensional matrix

which is an orthogonal projection projecting space  to
to  of the matrix
of the matrix  where
where  is an
is an  identity matrix and an
identity matrix and an  -dimensional matrix
-dimensional matrix

which is an orthogonal projection projecting space  to
to  of the transposed matrix
of the transposed matrix  where
where  is an
is an  identity matrix and
identity matrix and  is an
is an  -dimensional matrix pseudoinverse to the
-dimensional matrix pseudoinverse to the  -dimensional matrix
-dimensional matrix  . Using the property
. Using the property

where  , we will denote by
, we will denote by  a
a  -dimensional matrix constructed from
-dimensional matrix constructed from  linearly independent rows of the matrix
linearly independent rows of the matrix  . Moreover, taking into account the property
. Moreover, taking into account the property

we will denote by  an
an  -dimensional matrix constructed from
-dimensional matrix constructed from  linearly independent columns of the matrix
linearly independent columns of the matrix  .
.
Then (see [9, page 79, formulas ( ), (
), ( )]) the condition
)]) the condition

is necessary and sufficient for algebraic system (3.14) to be solvable where  is (throughout the paper) a
is (throughout the paper) a  -dimensional column zero vector. If such condition is true, system (3.14) has a solution
-dimensional column zero vector. If such condition is true, system (3.14) has a solution

Substituting the constant  defined by (3.22) into (3.13), we get a formula for a general solution of problem (3.11), (3.12):
defined by (3.22) into (3.13), we get a formula for a general solution of problem (3.11), (3.12):

where  is a generalized Green operator. If the vector functional
is a generalized Green operator. If the vector functional  satisfies the relation [9, page 176]
satisfies the relation [9, page 176]

which is assumed throughout the rest of the paper, then the generalized Green operator takes the form

where

is a generalized Green matrix, corresponding to the boundary value problem (3.11), (3.12), and the Cauchy matrix  has the form of (3.6). Therefore, the following theorem holds (see [10]).
has the form of (3.6). Therefore, the following theorem holds (see [10]).
Theorem 3.1.
Let  be defined by (3.15) and
be defined by (3.15) and  . Then the homogeneous problem
. Then the homogeneous problem

corresponding to the problem (3.11), (3.12) has exactly  linearly independent solutions
linearly independent solutions

Nonhomogeneous problem (3.11), (3.12) is solvable if and only if  and
and  satisfy
satisfy  linearly independent conditions (3.21). In that case, this problem has an
linearly independent conditions (3.21). In that case, this problem has an  -dimensional family of linearly independent solutions represented in an explicit analytical form (3.23).
-dimensional family of linearly independent solutions represented in an explicit analytical form (3.23).
The case of  implies the inequality
implies the inequality  . If
. If  , the boundary value problem is overdetermined, the number of boundary conditions is more than the number of unknowns, and Theorem 3.1 has the following corollary.
, the boundary value problem is overdetermined, the number of boundary conditions is more than the number of unknowns, and Theorem 3.1 has the following corollary.
Corollary 3.2.
If  , then the homogeneous problem (3.27) has only the trivial solution. Nonhomogeneous problem (3.11), (3.12) is solvable if and only if
, then the homogeneous problem (3.27) has only the trivial solution. Nonhomogeneous problem (3.11), (3.12) is solvable if and only if  and
and  satisfy
satisfy  linearly independent conditions (3.21) where
linearly independent conditions (3.21) where  Then the unique solution can be represented as
Then the unique solution can be represented as

The case of  is interesting as well. Then the inequality
is interesting as well. Then the inequality  , holds. If
, holds. If  the boundary value problem is not fully defined. In this case, Theorem 3.1 has the following corollary.
the boundary value problem is not fully defined. In this case, Theorem 3.1 has the following corollary.
Corollary 3.3.
If  , then the homogeneous problem (3.27) has an
, then the homogeneous problem (3.27) has an  -dimensional
-dimensional  family of linearly independent solutions
family of linearly independent solutions

Nonhomogeneous problem (3.11), (3.12) is solvable for arbitrary  and
and  and has an
and has an  -parametric family of solutions
-parametric family of solutions

Finally, combining both particular cases mentioned in Corollaries 3.2 and 3.3, we get a noncritical case.
Corollary 3.4.
If  (i.e.,
(i.e.,  ), then the homogeneous problem (3.27) has only the trivial solution. The nonhomogeneous problem (3.11), (3.12) is solvable for arbitrary
), then the homogeneous problem (3.27) has only the trivial solution. The nonhomogeneous problem (3.11), (3.12) is solvable for arbitrary  and
and  and has a unique solution
and has a unique solution

where

is a Green operator, and

is a related Green matrix, corresponding to the problem (3.11), (3.12).
4. Perturbed Boundary Value Problems
As an example of application of Theorem 3.1, we consider the problem of bifurcation from point  of solutions
of solutions  ,
,  satisfying, for a.e.
satisfying, for a.e.  , systems of ordinary differential equations
, systems of ordinary differential equations

where  is
is  constant matrix,
constant matrix,  is an
is an  matrix,
matrix,  , consisting of
, consisting of  matrices
matrices  ,
,  , having entries in
, having entries in  ,
,  is a small parameter, delays
is a small parameter, delays  are measurable on
are measurable on  ,
,  ,
,  ,
,  ,
,  ,
,  , and satisfying the initial and boundary conditions
, and satisfying the initial and boundary conditions

where  ,
,  is a given vector function with components in
is a given vector function with components in  , and
, and  is a linear vector functional. Using denotations (1.3), (1.4), and (1.6), it is easy to show that the perturbed nonhomogeneous linear boundary value problem (4.1), (4.2) can be rewritten as
is a linear vector functional. Using denotations (1.3), (1.4), and (1.6), it is easy to show that the perturbed nonhomogeneous linear boundary value problem (4.1), (4.2) can be rewritten as

In (4.3) we specify  as a single delay defined by formula
as a single delay defined by formula  ;
;

is an  -dimensional column vector, and
-dimensional column vector, and  is an
is an  -dimensional column vector given by
-dimensional column vector given by

It is easy to see that  . The operator
. The operator  maps the space
maps the space  into the space
into the space

that is,  . Using denotation (1.3) for the operator
. Using denotation (1.3) for the operator  , we have the following representation:
, we have the following representation:

where

is the characteristic function of the set

Assume that nonhomogeneities  and
and  are such that the shortened boundary value problem
are such that the shortened boundary value problem

being a particular case of (4.3) for  , does not have a solution. In such a case, according to Theorem 3.1, the solvability criterion (3.21) does not hold for problem (4.10). Thus, we arrive at the following question.
, does not have a solution. In such a case, according to Theorem 3.1, the solvability criterion (3.21) does not hold for problem (4.10). Thus, we arrive at the following question.
Is it possible to make the problem ( 4.10 ) solvable by means of linear perturbations and, if this is possible, then of what kind should the perturbations
 and the delays
and the delays
 ,
,
 be for the boundary value problem ( 4.3 ) to be solvable?
be for the boundary value problem ( 4.3 ) to be solvable?
We can answer this question with the help of the  -matrix
-matrix

where

constructed by using the coefficients of the problem (4.3).
Using the Vishik and Lyusternik method [11] and the theory of generalized inverse operators [9], we can find bifurcation conditions. Below we formulate a statement (proved using [8] and [9, page 177]) which partially answers the above problem. Unlike an earlier result [9], this one is derived in an explicit analytical form. We remind that the notion of a solution of a boundary value problem was specified in part 1.
Theorem 4.1.
Consider system

where  is
is  constant matrix,
constant matrix,  is an
is an  matrix,
matrix,  , consisting of
, consisting of  matrices
matrices  ,
,  , having entries in
, having entries in  ,
,  is a small parameter, delays
is a small parameter, delays  are measurable on
are measurable on  ,
,  ,
,  ,
,  ,
,  , with the initial and boundary conditions
, with the initial and boundary conditions

where  ,
,  is a given vector function with components in
is a given vector function with components in  , and
, and  is a linear vector functional, and assume that
is a linear vector functional, and assume that

(satisfying  ) and
) and  are such that the shortened problem
are such that the shortened problem

does not have a solution. If

then the boundary value problem (4.13), (4.14) has a set of  linearly independent solutions in the form of the series
linearly independent solutions in the form of the series

converging for fixed  , where
, where  is an appropriate constant characterizing the domain of the convergence of the series (4.18), and
is an appropriate constant characterizing the domain of the convergence of the series (4.18), and  are suitable coefficients.
are suitable coefficients.
Remark 4.2.
Coefficients  ,
,  , in (4.18) can be determined. The procedure describing the method of their deriving is a crucial part of the proof of Theorem 4.1 where we give their form as well.
, in (4.18) can be determined. The procedure describing the method of their deriving is a crucial part of the proof of Theorem 4.1 where we give their form as well.
Proof.
Substitute (4.18) into (4.3) and equate the terms that are multiplied by the same powers of  . For
. For  , we obtain the homogeneous boundary value problem
, we obtain the homogeneous boundary value problem

which determines  .
.
By Theorem 3.1, the homogeneous boundary value problem (4.19) has an  -parametric
-parametric  family of solutions
family of solutions  where the
where the  -dimensional column vector
-dimensional column vector  can be determined from the solvability condition of the problem for
can be determined from the solvability condition of the problem for  .
.
For  , we get the boundary value problem
, we get the boundary value problem

which determines  .
.
It follows from Theorem 3.1 that the solvability criterion (3.21) for problem (4.20) has the form

from which we receive, with respect to  , an algebraic system
, an algebraic system

The right-hand side of (4.22) is nonzero only in the case that the shortened problem does not have a solution. The system (4.22) is solvable for arbitrary  and
and  if the condition (4.17) is satisfied [9, page 79]. In this case, system (4.22) becomes resolvable with respect to
if the condition (4.17) is satisfied [9, page 79]. In this case, system (4.22) becomes resolvable with respect to  up to an arbitrary constant vector
up to an arbitrary constant vector  from the null-space of matrix
from the null-space of matrix  and
and

This solution can be rewritten in the form

where

and  is an
is an  -dimensional matrix whose columns are a complete set of
-dimensional matrix whose columns are a complete set of  linearly independent columns of the
linearly independent columns of the  -dimensional matrix
-dimensional matrix  with
with

So, for the solutions of the problem (3.14), we have the following formulas:

Assuming that (3.24) and (4.17) hold, the boundary value problem (4.20) has the  -parametric family of solutions
-parametric family of solutions

Here,  is an
is an  -dimensional constant vector, which is determined at the next step from the solvability condition of the boundary value problem for
-dimensional constant vector, which is determined at the next step from the solvability condition of the boundary value problem for 
For  , we get the boundary value problem
, we get the boundary value problem

which determines  . The solvability criterion for the problem (4.29) has the form (in computations below we need a composition of operators and the order of operations is following the inner operator
. The solvability criterion for the problem (4.29) has the form (in computations below we need a composition of operators and the order of operations is following the inner operator  which acts to matrices and vector function having an argument denoted by
which acts to matrices and vector function having an argument denoted by  and the outer operator
and the outer operator  which acts to matrices having an argument denoted by
which acts to matrices having an argument denoted by 

or, equivalently, the form

Assuming that (4.17) holds, the algebraic system (4.31) has the following family of solutions:

where

So, for the  -parametric family of solutions of the problem (4.20), we have the following formula:
-parametric family of solutions of the problem (4.20), we have the following formula:

where

Again, assuming that (4.17) holds, the boundary value problem (4.29) has the  -parametric family of solutions
-parametric family of solutions

Here,  is an
is an  -dimensional constant vector, which is determined at the next step from the solvability condition of the boundary value problem for
-dimensional constant vector, which is determined at the next step from the solvability condition of the boundary value problem for  :
:

The solvability criterion for the problem (4.37) has the form

or, equivalently, the form

Under condition (4.17), the last equation has the  -parametric family of solutions
-parametric family of solutions

where

So, for the coefficient  , we have the following formula:
, we have the following formula:

where

Continuing this process, by assuming that (4.17) holds, it follows by induction that the coefficients  of the series (4.18) can be determined, from the relevant boundary value problems as follows:
of the series (4.18) can be determined, from the relevant boundary value problems as follows:

where

and  .
.
The convergence of the series (4.18) can be proved by traditional methods of majorization [9, 11].
In the case  , the condition (4.17) is equivalent with
, the condition (4.17) is equivalent with  , and problem (4.13), (4.14) has a unique solution.
, and problem (4.13), (4.14) has a unique solution.
Example 4.3.
Consider the linear boundary value problem for the delay differential equation

where, as in the above,  and
and  are measurable functions. Using the symbols
are measurable functions. Using the symbols  and
and  (see (1.3), (1.4), (1.6), and (4.7)), we arrive at the following operator system:
(see (1.3), (1.4), (1.6), and (4.7)), we arrive at the following operator system:

where  is an
is an  matrix
matrix  , and
, and

Under the condition that the generating boundary value problem has no solution, we consider the simplest case of  . Using the delayed matrix exponential (2.5), it is easy to see that, in this case,
. Using the delayed matrix exponential (2.5), it is easy to see that, in this case,  is a normal fundamental matrix for the homogeneous unperturbed system
is a normal fundamental matrix for the homogeneous unperturbed system  , and
, and

Then the  matrix
matrix  has the form
has the form

If  , problem (4.46) has a unique solution
, problem (4.46) has a unique solution  with the properties
with the properties

Let, say,  where
where  ,
,  , then
, then

or, equivalently,

Now the matrix  turns into
turns into

and the boundary value problem (4.46) is uniquely solvable if

References
Azbelev NV, Maksimov VP: Equations with retarded argument. Journal of Difference Equations and Applications 1983,18(12):1419-1441. translation from Differentsial'nye Uravneniya, vol. 18, no. 12, pp. 2027–2050, 1982
Schwabik Š, Tvrdý M, Vejvoda O: Differential and Integral Equations, Boundary Value Problems and Adjoint. Reidel, Dordrecht, The Netherlands; 1979.
Maksimov VP, Rahmatullina LF: A linear functional-differential equation that is solved with respect to the derivative. Differentsial'nye Uravneniya 1973, 9: 2231-2240.
Azbelev NV, Maksimov VP, Rakhmatullina LF: Introduction to the Theory of Functional Differential Equations: Methods and Applications, Contemporary Mathematics and Its Applications. Volume 3. Hindawi Publishing Corporation, New York, NY, USA; 2007:x+314.
Hale J: Theory of Functional Differential Equations, Applied Mathematical Sciences. Volume 3. 2nd edition. Springer, New York, NY, USA; 1977:x+365.
Mallet-Paret J: The Fredholm alternative for functional-differential equations of mixed type. Journal of Dynamics and Differential Equations 1999,11(1):1-47. 10.1023/A:1021889401235
Khusainov DYa, Shuklin GV: On relative controllability in systems with pure delay. International Applied Mechanics 2005,41(2):210-221. translation from Prikladnaya Mekhanika, vol. 41, no. 2, pp.118–130, 2005 10.1007/s10778-005-0079-3
Boichuk AA, Grammatikopoulos MK: Perturbed Fredholm boundary value problems for delay differential systems. Abstract and Applied Analysis 2003, (15):843-864. 10.1155/S1085337503304026
Boichuk AA, Samoilenko AM: Generalized Inverse Operators and Fredholm Boundary-Value Problems. VSP, Utrecht, The Netherlands; 2004:xiv+317.
Boichuk AA, Diblík J, Khusainov DYa, Růžičková M: Fredholm's boundary-value problems for differential systems with a single delay. Nonlinear Analysis 2010,72(5):2251-2258. 10.1016/j.na.2009.10.025
Vishik MI, Lyusternik LA: The solution of some perturbation problems for matrices and selfadjoint differential equations. I. Russian Mathematical Surveys 1960,15(3):1-73. translation from Uspekhi Matematicheskikh Nauk, vol. 15, no. 3(93), pp. 3–80, 1960 10.1070/RM1960v015n03ABEH004092
Acknowledgments
The authors highly appreciate the work of the anonymous referee whose comments and suggestions helped them greatly to improve the quality of the paper in many aspects. The first author was supported by Grant 1/0771/08 of the Grant Agency of Slovak Republic (VEGA) and Project APVV-0700-07 of Slovak Research and Development Agency. The second author was supported by Grant 201/08/0469 of Czech Grant Agency and by the Council of Czech Government MSM 0021630503, MSM 0021630519, and MSM 0021630529. The third author was supported by Project M/34-2008 of Ukrainian Ministry of Education. The fourth author was supported by Grant 1/0090/09 of the Grant Agency of Slovak Republic (VEGA) and project APVV-0700-07 of Slovak Research and Development Agency.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Boichuk, A., Diblík, J., Khusainov, D. et al. Boundary Value Problems for Delay Differential Systems. Adv Differ Equ 2010, 593834 (2010). https://doi.org/10.1155/2010/593834
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/593834
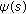 is an arbitrary continuously differentiable vector function can be represented in the form
is an arbitrary continuously differentiable vector function can be represented in the form 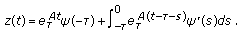
 if
if 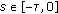 can be represented in the form
can be represented in the form