- Research Article
- Open access
- Published:
On the Global Character of the System of Piecewise Linear Difference Equations  and
and 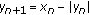
Advances in Difference Equations volume 2010, Article number: 573281 (2010)
Abstract
We consider the system in the title where the initial condition  We show that the system has exactly two prime period-5 solutions and a unique equilibrium point
We show that the system has exactly two prime period-5 solutions and a unique equilibrium point  . We also show that every solution of the system is eventually one of the two prime period-5 solutions or else the unique equilibrium point.
. We also show that every solution of the system is eventually one of the two prime period-5 solutions or else the unique equilibrium point.
1. Introduction
In this paper, we consider the system of piecewise linear difference equations

where the initial condition  . We show that every solution of System (1.1) is eventually either one of two prime period-5 solutions or else the unique equilibrium point
. We show that every solution of System (1.1) is eventually either one of two prime period-5 solutions or else the unique equilibrium point  .
.
System (1.1) was motivated by Devaney's Gingerbread man map [1, 2]

or its equivalent system of piecewise linear difference equations [3, 4]

We believe that the methods and techniques used in this paper will be useful in discovering the global character of solutions of similar systems, including the Gingerbread man map.
2. The Global Behavior of the Solutions of System (1.1)
System (1.1) has the equilibrium point  given by
given by

System (1.1) has two prime period-5 solutions,

Set

Theorem 2.1.
Let  . Then there exists an integer
. Then there exists an integer  such that the solution
such that the solution  is eventually either the prime period-5 solution
is eventually either the prime period-5 solution  , the prime period-5 solution
, the prime period-5 solution  , or else the unique equilibrium point
, or else the unique equilibrium point  .
.
The proof is a direct consequence of the following lemmas.
Lemma 2.2.
Suppose there exists an integer  such that
such that  and
and  . Then
. Then  , and so
, and so  is the equilibrium solution.
is the equilibrium solution.
Proof.
Note that

and so the proof is complete.
Lemma 2.3.
Suppose there exists an integer  such that
such that  and
and  . Then
. Then  , and so
, and so  is
is  .
.
Proof.
We have

and so the proof is complete.
Lemma 2.4.
Suppose there exists an integer  such that
such that  and
and  . Then the following statements are true.
. Then the following statements are true.
-
(1)
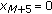 .
. -
(2)
If
 , then
, then  is
is 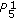 .
. -
(3)
If
 , then
, then 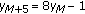 .
.
Proof.
We have  and
and  . Then
. Then

and so statement (1) is true.
If  , then
, then  . That is,
. That is,  and so statement (2) is true.
and so statement (2) is true.
If  , then
, then  , and so statement (3) is true.
, and so statement (3) is true.
Lemma 2.5.
Suppose there exists an integer  such that
such that  and
and  . Then the following statements are true.
. Then the following statements are true.
-
(1)
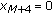 .
. -
(2)
If
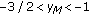 , then
, then  .
. -
(3)
If
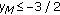 , then
, then 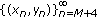 is
is 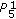 .
.
Proof.
We have  and
and  . Then
. Then

and so statement (1) is true.
Now if  , then
, then  . Thus
. Thus  , and so statement (2) is true.
, and so statement (2) is true.
Lastly, if  , then
, then  . Thus
. Thus  ; that is,
; that is,  and so statement (3) is true.
and so statement (3) is true.
Lemma 2.6.
Suppose there exists an integer  such that
such that  and
and  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
 , then
, then  is
is  .
. -
(2)
If
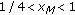 , then
, then 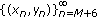 is
is 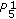 .
. -
(3)
If
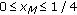 , then
, then  and
and 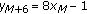 .
.
Proof.
First consider the case  and
and  . Then
. Then

and so statement (1) is true.
Next consider the case  and
and  . Then
. Then

If  , then
, then  and so
and so  . That is,
. That is,  and so statement (2) is true.
and so statement (2) is true.
If  , then
, then  . Thus
. Thus  , and so statement (3) is true.
, and so statement (3) is true.
Lemma 2.7.
Suppose there exists an integer  such that
such that  and
and  . Then the following statements are true.
. Then the following statements are true.
-
(1)
 .
. -
(2)
If
 , then
, then 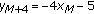 .
. -
(3)
If
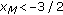 , then
, then 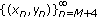 is
is 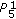 .
.
Proof.
Let  and
and  . Then
. Then

and so statement (1) is true.
If  , then
, then  . Thus
. Thus  , and so statement (2) is true.
, and so statement (2) is true.
If  , then
, then  and
and  . That is,
. That is,  and so
and so  is
is  and the proof is complete.
and the proof is complete.
We now give the proof of Theorem 2.1 when  is in
is in  .
.
Lemma 2.8.
Suppose there exists an integer  such that
such that  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
 , then
, then 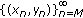 is eventually the equilibrium solution.
is eventually the equilibrium solution. -
(2)
If
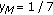 , then the solution
, then the solution 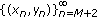 is
is 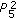 .
. -
(3)
If
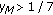 , then the solution
, then the solution 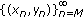 is eventually
is eventually  .
.
Proof.
-
(1)
We will first show that statement (1) is true. Suppose
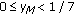 ; for each
; for each 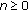 , let
, let 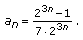 (2.11)
(2.11)
Observe that

Thus there exists a unique integer  such that
such that  .
.
We first consider the case  ; that is,
; that is,  . By statements (1) and (3) of Lemma 2.4,
. By statements (1) and (3) of Lemma 2.4,  and
and  . Clearly
. Clearly  , and so
, and so

Now  and
and  , and so by Lemma 2.2,
, and so by Lemma 2.2,  is the equilibrium solution.
is the equilibrium solution.
Without loss of generality, we may assume  .
.
For each integer  such that
such that  , let
, let  be the following statement:
be the following statement:

Claim 1.
 is true for
is true for  .
.
The proof Claim 1 will be by induction on  . We will first show that
. We will first show that  is true.
is true.
Recall that  and
and  . Then by statements (1) and (3) of Lemma 2.4, we have
. Then by statements (1) and (3) of Lemma 2.4, we have  and
and  .
.
Note that,

and so  is true. Thus if
is true. Thus if  , then we have shown that for
, then we have shown that for  ,
,  is true. It remains to consider the case
is true. It remains to consider the case  . So assume that
. So assume that  . Let
. Let  be an integer such that
be an integer such that  and suppose
and suppose  is true. We will show that
is true. We will show that  is true.
is true.
Since  is true, we know
is true, we know

It is easy to verify that for  ,
,

Thus by statements (1) and (3) of Lemma 2.4,

Recall that  .
.
In particular,

and so  is true. Thus the proof of the claim is complete. That is,
is true. Thus the proof of the claim is complete. That is,  is true for
is true for  . Specifically,
. Specifically,  is true, and so
is true, and so

In particular,

That is,  , and so by case
, and so by case  ,
,  is the equilibrium solution, and the proof of statement (1) is complete.
is the equilibrium solution, and the proof of statement (1) is complete.
-
(2)
We will next show that statement (2) is true. Suppose
 . Note that
. Note that 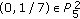 . Thus the solution
. Thus the solution 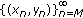 is
is  .
. -
(3)
Finally, we will show that statement (3) is true. Suppose
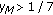 .
.
First consider  . By statement (2) of Lemma 2.4, the solution
. By statement (2) of Lemma 2.4, the solution  is
is  .
.
Next consider the case  . For each
. For each  , let
, let

Observe that

Thus there exists a unique integer  such that
such that  .
.
Note that the statement  which we stated and proved in the proof of statement (1) of this lemma still holds. Specifically
which we stated and proved in the proof of statement (1) of this lemma still holds. Specifically  is true, and so
is true, and so

Recall that for  .
.
In particular,

By statement (2) of Lemma 2.4, the solution  is
is  .
.
We now give the proof of Theorem 2.1 when  is in
is in  .
.
Lemma 2.9.
Suppose there exists an integer  such that
such that  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
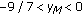 , then
, then 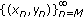 is eventually the equilibrium solution.
is eventually the equilibrium solution. -
(2)
If
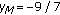 , then the solution
, then the solution 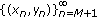 is
is  .
. -
(3)
If
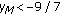 , then the solution
, then the solution 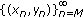 is eventually
is eventually 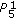 .
.
Proof.
-
(1)
We will first show that statement (1) is true. So suppose
 .
.
Case 1.
Suppose  . Then
. Then

In particular,  and
and  , and so by Lemma 2.2,
, and so by Lemma 2.2,  is the equilibrium solution.
is the equilibrium solution.
Case 2.
Suppose  . By statements (1) and (2) of Lemma 2.5,
. By statements (1) and (2) of Lemma 2.5,  and
and  . Then
. Then

Thus  and
and  , and so by Lemma 2.2,
, and so by Lemma 2.2,  is the equilibrium solution.
is the equilibrium solution.
Case 3.
Suppose  . By statements (1) and (2) of Lemma 2.5,
. By statements (1) and (2) of Lemma 2.5,  and
and  . Note that
. Note that  and so by statement (1) of Lemma 2.8,
and so by statement (1) of Lemma 2.8,  is eventually equilibrium solution.
is eventually equilibrium solution.
-
(2)
We will next show that statement (2) is true. Suppose
 . By direct calculations we have
. By direct calculations we have 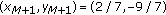 . So the solution
. So the solution 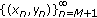 is
is 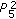 .
. -
(3)
Finally, we will show that statement (3) is true. Suppose
 and
and  .
.
Case 1.
Suppose  . By statements (1) and (2) of Lemma 2.5, we have
. By statements (1) and (2) of Lemma 2.5, we have  and
and  . Note that
. Note that  and so by statement (3) of Lemma 2.8, the solution
and so by statement (3) of Lemma 2.8, the solution  is eventually
is eventually  .
.
Case 2.
Suppose  . By statement (3) of Lemma 2.5, the solution
. By statement (3) of Lemma 2.5, the solution  is
is  .
.
We now give the proof of Theorem 2.1 when  is in
is in  .
.
Lemma 2.10.
Suppose there exists an integer  such that
such that  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
 , then
, then 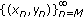 is eventually the equilibrium solution.
is eventually the equilibrium solution. -
(2)
If
 , then the solution
, then the solution  is
is 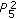 .
. -
(3)
If
 , then the solution
, then the solution 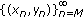 is eventually
is eventually 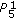 .
.
Proof.
-
(1)
We will first show that statement (1) is true. So suppose
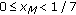 and
and  . By statement (3) of Lemma 2.6,
. By statement (3) of Lemma 2.6,  and
and  . In particular,
. In particular, 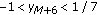 and so by statement (1) of Lemma 2.8 and statement (1) of Lemma 2.9,
and so by statement (1) of Lemma 2.8 and statement (1) of Lemma 2.9,  is eventually the equilibrium solution.
is eventually the equilibrium solution. -
(2)
We will next show that statement (2) is true. Suppose
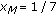 . By direct calculations we have
. By direct calculations we have 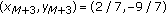 . Thus the solution
. Thus the solution 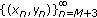 is
is  .
. -
(3)
Finally, we will show statement (3) is true.
First consider the case  . By statement (3) of Lemma 2.6,
. By statement (3) of Lemma 2.6,  and
and  . Now,
. Now,  and so by statement (3) of Lemma 2.8, the solution
and so by statement (3) of Lemma 2.8, the solution  is eventually
is eventually  .
.
Next consider the case  . Then by statements (1) and (2) of Lemma 2.6, if
. Then by statements (1) and (2) of Lemma 2.6, if  then
then  is
is  , and if
, and if  then
then  is
is  .
.
We next give the proof of Theorem 2.1 when  is in
is in  .
.
Lemma 2.11.
Suppose there exists an integer  such that
such that  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
 , then
, then 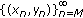 is eventually the equilibrium solution.
is eventually the equilibrium solution. -
(2)
If
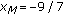 , then the solution
, then the solution  is
is 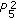 .
. -
(3)
If
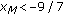 , then the solution
, then the solution  is eventually
is eventually 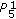 .
.
Proof.
-
(1)
We will first prove statement (1) is true. Suppose
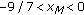 .
.
First consider the case  . Then
. Then

In particular,  and
and  and so by Lemma 2.2,
and so by Lemma 2.2,  is the equilibrium solution.
is the equilibrium solution.
Next consider the case  . By statements (1) and (2) of Lemma 2.7,
. By statements (1) and (2) of Lemma 2.7,  and
and  . In particular,
. In particular,  and so by statement (1) of Lemma 2.8 and statement (1) of Lemma 2.9,
and so by statement (1) of Lemma 2.8 and statement (1) of Lemma 2.9,  is eventually the equilibrium solution.
is eventually the equilibrium solution.
-
(2)
We will next show that statement (2) is true. Suppose
 . By direct calculations, we have
. By direct calculations, we have  . That is,
. That is, 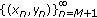 is
is  .
. -
(3)
Lastly, we will show that statement (3) is true. Suppose
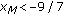 .
.
First consider the case  . By statements (1) and (2) of Lemma 2.7,
. By statements (1) and (2) of Lemma 2.7,  and
and  . In particular,
. In particular,  and so by statement (3) of Lemma 2.8, the solution
and so by statement (3) of Lemma 2.8, the solution  is eventually
is eventually  .
.
Next consider the case  . By statement (3) of Lemma 2.7, the solution
. By statement (3) of Lemma 2.7, the solution  is
is  .
.
We next give the proof of Theorem 2.1 when  is in
is in  .
.
Lemma 2.12.
Suppose there exists an integer  such that
such that  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
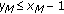 , then the solution
, then the solution  is
is 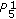 .
. -
(2)
If
 , then there exists an integer
, then there exists an integer 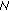 such that
such that 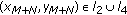 .
.
Proof.
Suppose  and
and  .
.
Then

Case 1.
Suppose  . Then, in particular,
. Then, in particular,  and
and  . Thus
. Thus

and so statement (1) is true.
Case 2.
Suppose  . Then, in particular,
. Then, in particular,  .
.
Subcase 1.
Suppose  .
.
Then  . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that  . Hence
. Hence  .
.
Subcase 2.
Suppose  .
.
Then  . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that  . Hence
. Hence  , and the proof is complete.
, and the proof is complete.
We next give the proof of Theorem 2.1 when  is in
is in  .
.
Lemma 2.13.
Suppose there exists an integer  such that
such that  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
 , then the solution
, then the solution 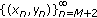 is the equilibrium solution.
is the equilibrium solution. -
(2)
If
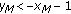 , then
, then 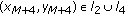 .
.
Proof.
By assumption, we have  and
and  .
.
If  , then
, then

Hence  is the equilibrium solution and statement (1) is true.
is the equilibrium solution and statement (1) is true.
If  , then it follows by a straight forward computation, which will be omitted, that
, then it follows by a straight forward computation, which will be omitted, that  . Thus
. Thus  and statement (2) is true.
and statement (2) is true.
We next give the proof of Theorem 2.1 when  is in
is in  .
.
Lemma 2.14.
Suppose there exists an integer  such that
such that  . Then the following statements are true.
. Then the following statements are true.
-
(1)
If
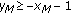 , then
, then 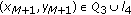 .
. -
(2)
If
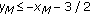 , then
, then 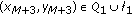 .
. -
(3)
If
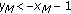 ,
, 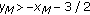 and
and  , then
, then 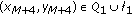 .
. -
(4)
If
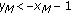 ,
, 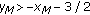 ,
, 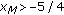 and
and  , then
, then  .
. -
(5)
If
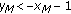 ,
, 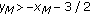 ,
, 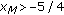 and
and 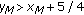 , then
, then  .
.
Proof.
Now  and
and  .
.
-
(1)
If
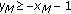 , then
, then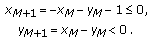 (2.32)
(2.32)Thus
 .
. -
(2)
If
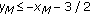 , then
, then 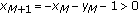 . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that (2.33)
(2.33)Hence
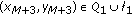 .
. -
(3)
If
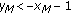 ,
, 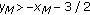 , and
, and 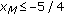 , then
, then  . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that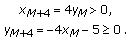 (2.34)
(2.34)Thus
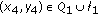 .
. -
(4)
If
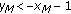 ,
, 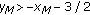 ,
,  , and
, and 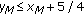 , then
, then 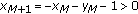 . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that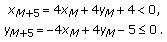 (2.35)
(2.35)Thus
 .
. -
(5)
Finally, suppose that
 ,
, 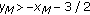 ,
, 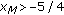 , and
, and 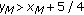 . Then
. Then  . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that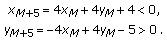 (2.36)
(2.36)Note that
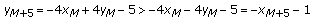 (2.37)
(2.37)and so by the first statement of this Lemma,
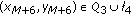 .
.
Thus we see that if there exists an integer  such that
such that  , then the proof of Theorem 2.1 is complete. Finally, we consider the case where the initial condition
, then the proof of Theorem 2.1 is complete. Finally, we consider the case where the initial condition  .
.
Lemma 2.15.
Suppose there exists an integer  such that
such that  . Then there exists a positive integer
. Then there exists a positive integer  such that
such that  .
.
Proof.
Without loss of generality, it suffices to consider the case where

Now  , and hence
, and hence  and
and  .
.
Thus

We have  , and thus
, and thus

We also have  , and hence
, and hence

Finally, we have  , and so
, and so

In particular,  and hence
and hence  .
.
3. Conclusion
We have presented the complete results concerning the global character of the solutions to System (1.1). We divided the real plane into 8 sections and utilized mathematical induction, proof by iteration, and direct computations to show that every solution of System (1.1) is eventually either the prime period-5 solution  , the prime period-5 solution
, the prime period-5 solution  , or else the unique equilibrium point
, or else the unique equilibrium point  . The proofs involve careful consideration of the various cases and subcases.
. The proofs involve careful consideration of the various cases and subcases.
References
Devaney RL: A piecewise linear model for the zones of instability of an area-preserving map. Physica D 1984,10(3):387-393. 10.1016/0167-2789(84)90187-8
Peitgen HO, Saupe D (Eds): The Science of Fractal Images. Springer, New York, NY, USA; 1991.
Grove EA, Ladas G: Periodicities in Nonlinear Difference Equations. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2005.
Kulenović MRS, Merino O: Discrete Dynamical Systems and Difference Equations with Mathematica. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:xvi+344.
Acknowledgments
The authors would like to express their gratitude to the Strategic Scholarships Fellowships Frontier Research Networks, the Office of the Commission on Higher Education, and National Center for Genetic Engineering and Biotechnology.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tikjha, W., Lenbury, Y. & Lapierre, E. On the Global Character of the System of Piecewise Linear Difference Equations  and
and 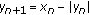 .
Adv Differ Equ 2010, 573281 (2010). https://doi.org/10.1155/2010/573281
.
Adv Differ Equ 2010, 573281 (2010). https://doi.org/10.1155/2010/573281
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/573281
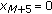 .
. , then
, then  is
is 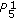 .
. , then
, then 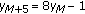 .
.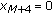 .
.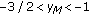 , then
, then  .
.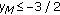 , then
, then 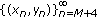 is
is 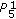 .
. , then
, then  is
is  .
.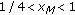 , then
, then 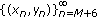 is
is 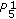 .
.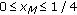 , then
, then  and
and 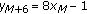 .
. .
. , then
, then 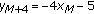 .
.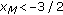 , then
, then 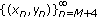 is
is 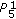 .
. , then
, then 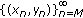 is eventually the equilibrium solution.
is eventually the equilibrium solution.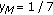 , then the solution
, then the solution 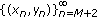 is
is 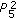 .
.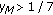 , then the solution
, then the solution 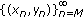 is eventually
is eventually  .
.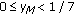 ; for each
; for each 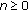 , let
, let 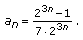
 . Note that
. Note that 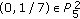 . Thus the solution
. Thus the solution 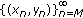 is
is  .
.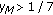 .
.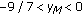 , then
, then 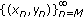 is eventually the equilibrium solution.
is eventually the equilibrium solution.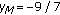 , then the solution
, then the solution 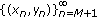 is
is  .
.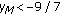 , then the solution
, then the solution 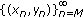 is eventually
is eventually 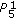 .
. .
. . By direct calculations we have
. By direct calculations we have 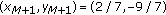 . So the solution
. So the solution 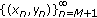 is
is 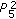 .
. and
and  .
. , then
, then 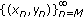 is eventually the equilibrium solution.
is eventually the equilibrium solution. , then the solution
, then the solution  is
is 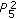 .
. , then the solution
, then the solution 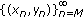 is eventually
is eventually 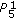 .
.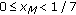 and
and  . By statement (3) of Lemma 2.6,
. By statement (3) of Lemma 2.6,  and
and  . In particular,
. In particular, 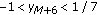 and so by statement (1) of Lemma 2.8 and statement (1) of Lemma 2.9,
and so by statement (1) of Lemma 2.8 and statement (1) of Lemma 2.9,  is eventually the equilibrium solution.
is eventually the equilibrium solution.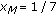 . By direct calculations we have
. By direct calculations we have 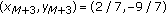 . Thus the solution
. Thus the solution 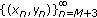 is
is  .
. , then
, then 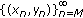 is eventually the equilibrium solution.
is eventually the equilibrium solution.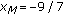 , then the solution
, then the solution  is
is 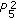 .
.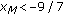 , then the solution
, then the solution  is eventually
is eventually 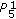 .
.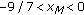 .
. . By direct calculations, we have
. By direct calculations, we have  . That is,
. That is, 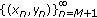 is
is  .
.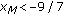 .
.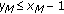 , then the solution
, then the solution  is
is 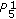 .
. , then there exists an integer
, then there exists an integer 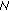 such that
such that 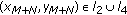 .
. , then the solution
, then the solution 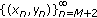 is the equilibrium solution.
is the equilibrium solution.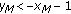 , then
, then 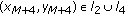 .
.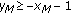 , then
, then 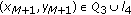 .
.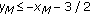 , then
, then 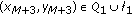 .
.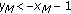 ,
, 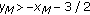 and
and  , then
, then 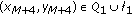 .
.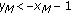 ,
, 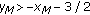 ,
, 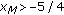 and
and  , then
, then  .
.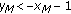 ,
, 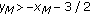 ,
, 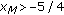 and
and 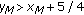 , then
, then  .
.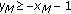 , then
, then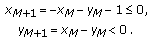
 .
.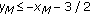 , then
, then 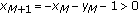 . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that
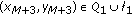 .
.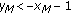 ,
, 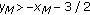 , and
, and 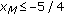 , then
, then  . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that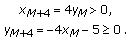
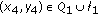 .
.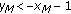 ,
, 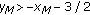 ,
,  , and
, and 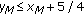 , then
, then 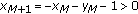 . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that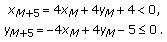
 .
. ,
, 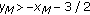 ,
, 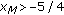 , and
, and 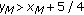 . Then
. Then  . It follows by a straight forward computation, which will be omitted, that
. It follows by a straight forward computation, which will be omitted, that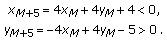
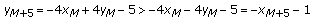
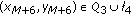 .
.