- Research Article
- Open access
- Published:
Complete Asymptotic and Bifurcation Analysis for a Difference Equation with Piecewise Constant Control
Advances in Difference Equations volume 2010, Article number: 542073 (2010)
Abstract
We consider a difference equation involving three parameters and a piecewise constant control function with an additional positive threshold  . Treating the threshold as a bifurcation parameter that varies between 0 and
. Treating the threshold as a bifurcation parameter that varies between 0 and  , we work out a complete asymptotic and bifurcation analysis. Among other things, we show that all solutions either tend to a limit 1-cycle or to a limit 2-cycle and, we find the exact regions of attraction for these cycles depending on the size of the threshold. In particular, we show that when the threshold is either small or large, there is only one corresponding limit 1-cycle which is globally attractive. It is hoped that the results obtained here will be useful in understanding interacting network models involving piecewise constant control functions.
, we work out a complete asymptotic and bifurcation analysis. Among other things, we show that all solutions either tend to a limit 1-cycle or to a limit 2-cycle and, we find the exact regions of attraction for these cycles depending on the size of the threshold. In particular, we show that when the threshold is either small or large, there is only one corresponding limit 1-cycle which is globally attractive. It is hoped that the results obtained here will be useful in understanding interacting network models involving piecewise constant control functions.
1. Introduction
Let  . In [1], Ge et al. obtained a complete asymptotic and bifurcation analysis of the following difference equation:
. In [1], Ge et al. obtained a complete asymptotic and bifurcation analysis of the following difference equation:

where  ,
,  , and
, and  is a nonlinear signal filtering control function of the form
is a nonlinear signal filtering control function of the form

in which the positive number  can be regarded as a threshold bifurcation parameter.
can be regarded as a threshold bifurcation parameter.
By adding a positive constant  to the right hand side of (1.1), we obtain the following equation:
to the right hand side of (1.1), we obtain the following equation:

Since  can be an arbitrary small positive number, (1.1) may be regarded as a limiting case of (1.3). Therefore, it would appear that the qualitative behavior of (1.3) will "degenerate into" that of (1.1) when
can be an arbitrary small positive number, (1.1) may be regarded as a limiting case of (1.3). Therefore, it would appear that the qualitative behavior of (1.3) will "degenerate into" that of (1.1) when  tends to 0. However, it is our intention to derive a complete asymptotic and bifurcation analysis for our new equation and show that, among other things, our expectation is not quite true and perhaps such discrepancy is due to the nonlinear nature of our model at hand.
tends to 0. However, it is our intention to derive a complete asymptotic and bifurcation analysis for our new equation and show that, among other things, our expectation is not quite true and perhaps such discrepancy is due to the nonlinear nature of our model at hand.
Indeed, we are dealing with a dynamical system with piecewise constant nonlinearlities (see e.g., [2–6]), and the usual linear and continuity arguments cannot be applied to our (1.3). Fortunately, we are able to achieve our goal by means of completely elementary considerations.
To this end, we first recall a few concepts. Note that given  , we may compute from (1.3) the numbers
, we may compute from (1.3) the numbers  in a unique manner. The corresponding sequence
in a unique manner. The corresponding sequence  is called the solution of (1.1) determined by or originated from the initial vector
is called the solution of (1.1) determined by or originated from the initial vector  .
.
Recall also that a positive integer  is a period of the sequence
is a period of the sequence  if
if  for all
for all  and that
and that  is the least or prime period of
is the least or prime period of  if
if  is the least among all periods of
is the least among all periods of  . The sequence
. The sequence  is said to be
is said to be  -periodic if
-periodic if  is its least period. The sequence
is its least period. The sequence  is said to be asymptotically periodic if there exist real numbers
is said to be asymptotically periodic if there exist real numbers  , where
, where  is a positive integer, such that
is a positive integer, such that

In case  is an
is an  -periodic sequence, we say that
-periodic sequence, we say that  is an asymptotically
is an asymptotically  -periodic sequence tending to the limit
-periodic sequence tending to the limit  -cycle (This term is introduced since the underlying concept is similar to that of the limit cycle in the theory of ordinary differential equations.)
-cycle (This term is introduced since the underlying concept is similar to that of the limit cycle in the theory of ordinary differential equations.)  . In particular, an asymptotically 1-periodic sequence is a convergent sequence and conversely.
. In particular, an asymptotically 1-periodic sequence is a convergent sequence and conversely.
Suppose that  is the set of all solutions of (1.1) that tend to the limit cycle
is the set of all solutions of (1.1) that tend to the limit cycle  . Then, the set
. Then, the set

is called the the region of attraction of the limit cycle  . In other words,
. In other words,  attracts all solutions originated from its region of attraction.
attracts all solutions originated from its region of attraction.
Equation (1.3) is related to several linear recurrence and functional inequality relations of the form




where  and
and  . Therefore, the following facts will be needed, which can easily be established by induction.
. Therefore, the following facts will be needed, which can easily be established by induction.
-
(i)
If
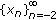 is a sequence which satisfies (1.6), then
is a sequence which satisfies (1.6), then

-
(ii)
If
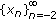 is a sequence which satisfies (1.7), then
is a sequence which satisfies (1.7), then

-
(iii)
If
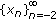 is a sequence which satisfies (1.8), then
is a sequence which satisfies (1.8), then

-
(iv)
If
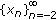 is a sequence which satisfies (1.9), then
is a sequence which satisfies (1.9), then

We will discuss solutions  of (1.3) originated from different
of (1.3) originated from different  and
and  in
in  . For this reason, we let
. For this reason, we let  and
and

Then, for  ,
,

Since

we see that  and
and

Similarly, let  and
and

Then,

Since  , we see further that
, we see further that

Note that (1.3) is equivalent to the following two dimensional dynamical system

by means of the identification  for
for  . Therefore, our subsequent results can be interpreted in terms of the dynamics of plane vector sequences defined by (1.21).
. Therefore, our subsequent results can be interpreted in terms of the dynamics of plane vector sequences defined by (1.21).
In particular, the following result states that a solution  of (1.21) with
of (1.21) with  will have one of its terms in
will have one of its terms in  .
.
Lemma 1.1.
Let  be a solution of (1.3). If
be a solution of (1.3). If  , then there is
, then there is  such that
such that  and
and  .
.
Proof.
Suppose to the contrary that  for all
for all  . Then, by (1.3),
. Then, by (1.3),

This, in view of (1.10) and (1.11), leads us to

which is a contradiction. Thus, there is  such that
such that  and
and  . Furthermore,
. Furthermore,

The proof is complete.
In the following discussions, we will allow the bifurcation parameter  to vary from
to vary from  to
to  . Indeed, we will consider five cases: (i)
. Indeed, we will consider five cases: (i)  , (ii)
, (ii)  , (iii)
, (iii)  , (iv)
, (iv)  , and (v)
, and (v)  and show that each solution of (1.1) tend to the limit cycles
and show that each solution of (1.1) tend to the limit cycles

Furthermore, in each case, we find the exact regions of attraction of the limit cycles. Then we describe our results in terms of our phase plane model (1.21) and compare them with what we have obtained for the phase plane model of (1.1).
We remark that since we need to find the exact regions of attraction, we need to consider initial vectors  belonging to (up to 9) different parts of the plane. Therefore the following derivations will seem to be repetitive. Fortunately, the principles behind our derivations are quite similar, and therefore some of the repetitive arguments can be simplified.
belonging to (up to 9) different parts of the plane. Therefore the following derivations will seem to be repetitive. Fortunately, the principles behind our derivations are quite similar, and therefore some of the repetitive arguments can be simplified.
For the sake of convenience, if no confusion is caused, the function  is also denoted by
is also denoted by  in the sequel.
in the sequel.
2. The Case Where 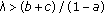
In this section, we assume that  .
.
Lemma 2.1.
Suppose that  . Let
. Let  be a solution of (1.3). Then, there is
be a solution of (1.3). Then, there is  such that
such that  .
.
Proof.
If  for all
for all  , then by (1.3),
, then by (1.3),  for
for  . One sees from (1.10) and (1.11) that
. One sees from (1.10) and (1.11) that  which is a contradiction. Hence, there must exist a
which is a contradiction. Hence, there must exist a  such that
such that  . If
. If  , we are done. Otherwise, one sees that
, we are done. Otherwise, one sees that

Repeating the argument we either find  such that
such that  , or one has that the subsequence
, or one has that the subsequence  lies in
lies in  whereas
whereas  . This would mean that the subsequence
. This would mean that the subsequence  satisfies (1.6) or (1.7) for
satisfies (1.6) or (1.7) for  , and hence
, and hence  , a contradiction. The proof is complete.
, a contradiction. The proof is complete.
Theorem A
Suppose  . Then every solution
. Then every solution  of (1.3) converges to
of (1.3) converges to  .
.
Proof.
In view of Lemma 2.1, we may suppose without loss of generality that  . Since
. Since  , we have
, we have

and by induction  for all
for all  . Thus, by (1.3),
. Thus, by (1.3),  for
for  . In view of (1.10) and (1.11),
. In view of (1.10) and (1.11),  . The proof is complete.
. The proof is complete.
3. The Case Where 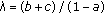
In this section, we suppose that  . Then,
. Then,  . Let
. Let  and
and

Then,

For the sake of convenience, let us set

Lemma 3.1.
Suppose that  . Let
. Let  be a solution of (1.3). If
be a solution of (1.3). If  , then there is
, then there is  such that
such that  .
.
Proof.
We break up  into four different parts
into four different parts  ,
,  ,
,  , and
, and  . We also let
. We also let  and
and  .
.
Clearly, there is nothing to prove if  .
.
Next, suppose that  . Then
. Then  for some
for some  . If
. If  , then by (1.3),
, then by (1.3),

That is,  . If
. If  for some
for some  , then
, then

Hence,  . By induction, we see that
. By induction, we see that  and hence,
and hence,  .
.
Suppose  . Then by (1.3),
. Then by (1.3),  . Hence,
. Hence, 
Suppose that  . Then by Lemma 1.1, there is
. Then by Lemma 1.1, there is  such that
such that  .
.
Suppose that  . Then
. Then  for some
for some  . If
. If  , then in view of (1.3),
, then in view of (1.3),

Hence,  . If
. If  for some
for some  , then by (1.3),
, then by (1.3),

Hence,  , and by induction,
, and by induction,  . Thus
. Thus  .
.
Suppose  . Then
. Then  for some
for some  . As in the previous case, we may show by similar arguments that
. As in the previous case, we may show by similar arguments that  .
.
Therefore, in the last four cases, we may apply the first two cases to conclude our proof. The proof is complete.
Theorem B
Suppose that  . Then, every solution of (1.3) with
. Then, every solution of (1.3) with  tends to
tends to  .
.
Proof.
Indeed, in view of Lemma 3.1, we may assume without loss of generality that  . Then, the same arguments in the proof of Theorem
. Then, the same arguments in the proof of Theorem  holds so that
holds so that  .
.
Lemma 3.2.
Suppose that  . Let
. Let  be a solution of (1.3). If
be a solution of (1.3). If  , then there is
, then there is  such that
such that  and
and  .
.
Proof.
We break up  into five different parts
into five different parts  ,
,  ,
,  ,
,  , and
, and  .
.
Clearly, there is nothing to prove if  .
.
Next, suppose that  . Then, by (1.3),
. Then, by (1.3),  . Hence,
. Hence,  .
.
Next, suppose that  . If
. If  for all
for all  , then, by (1.3),
, then, by (1.3),  for
for  . In view of (1.10) and (1.11),
. In view of (1.10) and (1.11),

which is a contradiction. Thus there is  such that
such that  and
and  . Hence,
. Hence, .
.
Next suppose that  . Then,
. Then,  for some
for some  . If
. If  , then by (1.3),
, then by (1.3),

Hence,  . If
. If  for some
for some  , then
, then

we see that  . By induction, we may further see that
. By induction, we may further see that  . Hence,
. Hence,  .
.
Next, suppose that  . Then
. Then  for some
for some  . By arguments similar to the previous case, we may then, show that
. By arguments similar to the previous case, we may then, show that  . The proof is complete.
. The proof is complete.
Theorem C
Suppose that  . Then, any solution
. Then, any solution  with
with  tends to the limit 2-cycle
tends to the limit 2-cycle  .
.
Proof.
In view of Lemma 3.2, we may assume without loss of generality that  and
and  . Then, by (1.3),
. Then, by (1.3),

and by induction  and
and  for all
for all  . Hence, by (1.3),
. Hence, by (1.3),  and
and  for
for  . In view of (1.10) and (1.11),
. In view of (1.10) and (1.11),  and
and  . The proof is complete.
. The proof is complete.
4. The Case Where 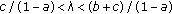
In this section, we suppose  . Then,
. Then,  .
.
Lemma 4.1.
Suppose that  . Let
. Let  be a solution of (1.3). Then, there is
be a solution of (1.3). Then, there is  such that
such that  and
and  .
.
Proof.
We break up the plane into seven different parts:  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
Clearly there is nothing to prove if  .
.
Next, suppose that  . Then, by (1.3),
. Then, by (1.3),  , and hence
, and hence  .
.
Next, suppose that  . If
. If  for all
for all  , then by (1.3),
, then by (1.3),  for
for  , which leads us to
, which leads us to  , which is a contradiction. Hence, there is
, which is a contradiction. Hence, there is  such that
such that  and
and  . Therefore,
. Therefore,  .
.
Next, suppose that  . If
. If  for all
for all  , then, by (1.3),
, then, by (1.3),  for
for  , which leads us to the contradiction
, which leads us to the contradiction  . Thus there is
. Thus there is  such that
such that  and
and  . Then
. Then  and hence,
and hence,  .
.
Next, suppose that  . Then, by (1.3) and induction, it is easily seen that
. Then, by (1.3) and induction, it is easily seen that  for all
for all  . If
. If  for all
for all  , then by (1.3),
, then by (1.3),

In view of (1.12),  , which is a contradiction. Hence, there is
, which is a contradiction. Hence, there is  such that
such that  .
.
Next, suppose that  . Then,
. Then,  . Hence,
. Hence,  .
.
Finally, suppose that  . Then, by Lemma 1.1, there is
. Then, by Lemma 1.1, there is  such that
such that  .
.
Therefore, in the last three cases, we may apply the conclusions in the first four cases to conclude our proof. The proof is complete.
Theorem D
Suppose that  . Then any solution
. Then any solution  of (1.3) tends to the limit 2-cycle
of (1.3) tends to the limit 2-cycle  .
.
Proof.
Indeed, in view of Lemma 4.1, we may assume without loss of generality that  and
and  . Then the same arguments in the proof of Theorem
. Then the same arguments in the proof of Theorem  then shows that
then shows that  and
and  .
.
5. The Case Where 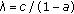
In this section, we assume that  . Then
. Then  .
.
Lemma 5.1.
Suppose that  . Let
. Let  be a solution of (1.3). If
be a solution of (1.3). If  , Then, there is
, Then, there is  such that
such that  and
and  .
.
Proof.
We break up the set  into eight different parts:
into eight different parts:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
Clearly, there is nothing to prove if  .
.
Next, suppose that  . If
. If  for all
for all  , then by (1.3),
, then by (1.3),  for
for  . In view of (1.10) and (1.11), we obtain the contradiction.
. In view of (1.10) and (1.11), we obtain the contradiction.

Hence, there is  such that
such that  and
and  . Thus
. Thus  .
.
Next, suppose that  . Then, by (1.3),
. Then, by (1.3),  . Hence,
. Hence,  .
.
Next, suppose that  . Then,
. Then,  for some
for some  . If
. If  , then
, then

Hence,  . If
. If  for some
for some  , then
, then

we see that  . By induction, we see that
. By induction, we see that  . Hence,
. Hence,  .
.
Next, suppose that  . Then
. Then  for some
for some  . If
. If  , then
, then

Hence,  . If
. If  for some
for some  , then
, then

we see that  . By induction,
. By induction,  . Hence
. Hence  .
.
Next, suppose that  . Then, by (1.3),
. Then, by (1.3),  . Hence,
. Hence,  .
.
Next, suppose that  . Then,
. Then,  , and hence,
, and hence,  .
.
Finally suppose  . Then, by Lemma 1.1, there is
. Then, by Lemma 1.1, there is  such that
such that  .
.
Therefore, in the fourth, sixth, seventh, and the eigth cases, we may use the conclusions in the other cases to conclude our proof. The proof is complete.
Theorem E
Suppose that  . Then, any solution
. Then, any solution  with
with  tends to the limit 2-cycle
tends to the limit 2-cycle  .
.
Proof.
Indeed, in view of Lemma 5.1, we may assume without loss of generality that  . Then the same arguments in the proof of Theorem
. Then the same arguments in the proof of Theorem  shows that
shows that  and
and  .
.
Theorem F
Suppose that  . Then, any solution
. Then, any solution  of (1.3) with
of (1.3) with  tends to
tends to  .
.
Proof.
By (1.3),

and by induction,  for all
for all  . Hence,
. Hence,  for
for  , which leads us to
, which leads us to  . The proof is complete.
. The proof is complete.
6. The Case Where 
In this section, we suppose that  . Then
. Then  .
.
Lemma 6.1.
Suppose that  . Let
. Let  be a solution of (1.3). Then there is
be a solution of (1.3). Then there is  such that
such that  .
.
Proof.
If  for all
for all  , then by (1.3),
, then by (1.3),  for all
for all  . In view of (1.12) and (1.13), this is impossible, and hence, there must exist a
. In view of (1.12) and (1.13), this is impossible, and hence, there must exist a  such that
such that  . Then
. Then  . By induction, we see that the subsequence
. By induction, we see that the subsequence  lies in
lies in  , and hence
, and hence  for all
for all  . In view of (1.11),
. In view of (1.11),  . The proof is complete.
. The proof is complete.
Theorem G
Suppose that  . Then, every solution
. Then, every solution  of (1.3) converges to
of (1.3) converges to  .
.
Proof.
Indeed, in view of Lemma 6.1, we may assume without loss of generality that  . Then the same arguments in the proof of Theorem
. Then the same arguments in the proof of Theorem  shows that
shows that  .
.
7. Phase Plane Interpretation and Comparison Remarks
We first recall that (1.1) and (1.3) are equivalent to


respectively, by means of the identification  for
for 
Then, Theorem  states that when
states that when  , all solutions
, all solutions  of (7.2) tends to the point
of (7.2) tends to the point  , or equivalently, all solutions of (7.2) are "attracted" to the limit 1-cycle
, or equivalently, all solutions of (7.2) are "attracted" to the limit 1-cycle  , or equivalently, the limit 1-cycle
, or equivalently, the limit 1-cycle  is a global attractor. For the sake of convenience, let us set
is a global attractor. For the sake of convenience, let us set

Then the above statements can be restated as follows.
-
(i)
If
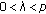 , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2).
attracts all solutions of (7.2). -
Similarly,
we may restate the other Theorems
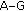 obtained previously as follows.
obtained previously as follows. -
(ii)
If
 , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2) originated from
attracts all solutions of (7.2) originated from  , and the limit 2-cycle
, and the limit 2-cycle  attracts all other solutions of (7.2).
attracts all other solutions of (7.2). -
(iii)
If
 , then the limit 2-cycle
, then the limit 2-cycle 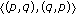 attracts all solutions of (7.2).
attracts all solutions of (7.2). -
(iv)
If
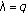 , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2) originated from
attracts all solutions of (7.2) originated from 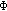 (see (3.3)), and the limit 2-cycle
(see (3.3)), and the limit 2-cycle  attracts all other solutions.
attracts all other solutions. -
(v)
If
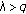 , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2).
attracts all solutions of (7.2).For comparison purposes, let us now recall the asymptotic results in [1]. Let us set
 (7.4)
(7.4) -
(vi)
If
 , then the limit 1-cycle
, then the limit 1-cycle 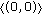 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 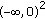 , and the limit 2-cycle
, and the limit 2-cycle  attracts all other solutions.
attracts all other solutions. -
(vii)
If
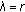 , then the limit 1-cycle
, then the limit 1-cycle 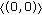 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 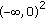 ; the limit 2-cycle
; the limit 2-cycle 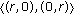 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 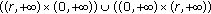 , and the limit 1-cycle
, and the limit 1-cycle 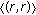 attracts all other solutions.
attracts all other solutions. -
(viii)
If
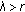 , then the limit 1-cycle
, then the limit 1-cycle 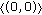 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 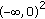 ; and the limit 1-cycle attracts all other solutions.
; and the limit 1-cycle attracts all other solutions.
In view of these statements, we see that for a small positive  , all solutions of (7.2) tend to a unique "lower" state vector, and for large
, all solutions of (7.2) tend to a unique "lower" state vector, and for large  , to another unique "higher" state vector. On the other hand, for a small positive
, to another unique "higher" state vector. On the other hand, for a small positive  , there are always solutions of (7.1) which tend to a limit 2-cycle, and solutions which tend to the limit 1-cycle
, there are always solutions of (7.1) which tend to a limit 2-cycle, and solutions which tend to the limit 1-cycle  , and for a large
, and for a large  , there are solutions of (7.1) which tend to the limit 1-cycle
, there are solutions of (7.1) which tend to the limit 1-cycle  and solutions to the limit 1-cycle
and solutions to the limit 1-cycle  . These observations show that it is probably not appropriate to call (1.1) the limiting case of (1.3)!
. These observations show that it is probably not appropriate to call (1.1) the limiting case of (1.3)!
Finally, we mention that network models such as the following

can be used to describe competing dynamics and it is hoped that our techniques, and results here will be useful in these studies.
References
Ge Q, Hou CM, Cheng SS: Complete asymptotic analysis of a nonlinear recurrence relation with threshold control. Advances in Difference Equations 2010, 2010:-19.
Zhu H, Huang L: Asymptotic behavior of solutions for a class of delay difference equation. Annals of Differential Equations 2005,21(1):99-105.
Yuan Z, Huang L, Chen Y: Convergence and periodicity of solutions for a discrete-time network model of two neurons. Mathematical and Computer Modelling 2002,35(9-10):941-950. 10.1016/S0895-7177(02)00061-4
Sedaghat H: Nonlinear Difference Equations, Mathematical Modelling: Theory and Applications. Volume 15. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:xvi+388.
di Bernardo M, Budd CJ, Champneys AR, Kowalczyk P: Piecewise Smooth Dynamical Systems. Springer, New York, NY, USA; 2008.
Hou C, Cheng SS: Eventually periodic solutions for difference equations with periodic coefficients and nonlinear control functions. Discrete Dynamics in Nature and Society 2008, 2008:-21.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hou, C., Han, L. & Cheng, S. Complete Asymptotic and Bifurcation Analysis for a Difference Equation with Piecewise Constant Control. Adv Differ Equ 2010, 542073 (2010). https://doi.org/10.1155/2010/542073
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/542073
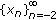 is a sequence which satisfies (1.6), then
is a sequence which satisfies (1.6), then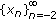 is a sequence which satisfies (1.7), then
is a sequence which satisfies (1.7), then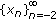 is a sequence which satisfies (1.8), then
is a sequence which satisfies (1.8), then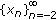 is a sequence which satisfies (1.9), then
is a sequence which satisfies (1.9), then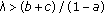
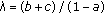
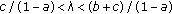
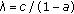

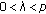 , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2).
attracts all solutions of (7.2).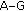 obtained previously as follows.
obtained previously as follows. , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2) originated from
attracts all solutions of (7.2) originated from  , and the limit 2-cycle
, and the limit 2-cycle  attracts all other solutions of (7.2).
attracts all other solutions of (7.2). , then the limit 2-cycle
, then the limit 2-cycle 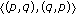 attracts all solutions of (7.2).
attracts all solutions of (7.2).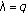 , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2) originated from
attracts all solutions of (7.2) originated from 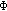 (see (3.3)), and the limit 2-cycle
(see (3.3)), and the limit 2-cycle  attracts all other solutions.
attracts all other solutions.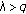 , then the limit 1-cycle
, then the limit 1-cycle  attracts all solutions of (7.2).
attracts all solutions of (7.2).
 , then the limit 1-cycle
, then the limit 1-cycle 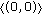 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 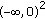 , and the limit 2-cycle
, and the limit 2-cycle  attracts all other solutions.
attracts all other solutions.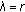 , then the limit 1-cycle
, then the limit 1-cycle 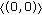 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 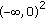 ; the limit 2-cycle
; the limit 2-cycle 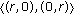 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 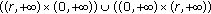 , and the limit 1-cycle
, and the limit 1-cycle 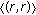 attracts all other solutions.
attracts all other solutions.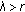 , then the limit 1-cycle
, then the limit 1-cycle 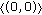 attracts all solutions of (7.1) originated from
attracts all solutions of (7.1) originated from 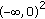 ; and the limit 1-cycle attracts all other solutions.
; and the limit 1-cycle attracts all other solutions.