- Research Article
- Open access
- Published:
Oscillatory Behavior of Quasilinear Neutral Delay Dynamic Equations on Time Scales
Advances in Difference Equations volume 2010, Article number: 450264 (2010)
Abstract
By means of the averaging technique and the generalized Riccati transformation technique, we establish some oscillation criteria for the second-order quasilinear neutral delay dynamic equations  ,
,  , where
, where  , and the time scale interval is
, and the time scale interval is  . Our results in this paper not only extend the results given by Agarwal et al. (2005) but also unify the oscillation of the second-order neutral delay differential equations and the second-order neutral delay difference equations.
. Our results in this paper not only extend the results given by Agarwal et al. (2005) but also unify the oscillation of the second-order neutral delay differential equations and the second-order neutral delay difference equations.
1. Introduction
The theory of time scales, which has recently received a lot of attention, was introduced by Hilger in his Ph.D. Thesis in 1988 in order to unify continuous and discrete analysis (see Hilger [1]). Several authors have expounded on various aspects of this new theory and references cited therein. A book on the subject of time scale, by Bohner and Peterson [2], summarizes and organizes much of the time scale calculus; we refer also the last book by Bohner and Peterson [3] for advances in dynamic equations on time scales.
A time scale  is an arbitrary closed subset of the reals, and the cases when this time scale is equal to the reals or to the integers represent the classical theories of differential and of difference equations. Many other interesting time scales exist (see Bohner and Peterson [2]).
is an arbitrary closed subset of the reals, and the cases when this time scale is equal to the reals or to the integers represent the classical theories of differential and of difference equations. Many other interesting time scales exist (see Bohner and Peterson [2]).
In the last few years, there has been much research activity concerning the oscillation and nonoscillation of solutions of various dynamic equations on time scales which attempts to harmonize the oscillation theory for the continuous and the discrete to include them in one comprehensive theory and to eliminate obscurity form both, for instance, the papers [4–20] and the reference cited therein.
For oscillation of delay dynamic equations on time scales, see recently papers [21–32]. However, there are very few results dealing with the oscillation of the solutions of neutral delay dynamic equations on time scales; we refer the reader to [33–44].
Agarwal et al. [33] and Saker [37] consider the second-order nonlinear neutral delay dynamic equations on time scales:

where  ,
,  is a quotient of odd positive integer,
is a quotient of odd positive integer,  are positive constants,
are positive constants,  such that
such that  for all nonzero
for all nonzero  , and there exists a nonnegative function
, and there exists a nonnegative function  defined on
defined on  satisfing
satisfing  .
.
Agwo [35] examines the oscillation of the second-order nonlinear neutral delay dynamic equations:

Li et al. [36] discuss the existence of nonoscillatory solutions to the second-order neutral delay dynamic equation of the form

Saker et al. [38, 39], Sahíner [40], and Wu et al. [43] consider the second-order neutral delay and mixed-type dynamic equations on time scales:

where  ,
,  is a quotient of odd positive integer,
is a quotient of odd positive integer,  ,
,  such that
such that  for all nonzero
for all nonzero  , and there exists a nonnegative function
, and there exists a nonnegative function  defined on
defined on  satisfing
satisfing  .
.
Zhu and Wang [44] study existence of nonoscillatory solutions to neutral dynamic equations on time scales:

Recently, Tripathy [42] has established some new oscillation criteria for second-order nonlinear delay dynamic equations of the form

where  ,
,  is a quotient of odd positive integer,
is a quotient of odd positive integer,  are positive constants,
are positive constants,  and
and  .
.
To the best of our knowledge, there are no results regarding the oscillation of the solutions of the following second-order nonlinear neutral delay dynamic equations on time scales up to now:

where  , and the time scale interval is
, and the time scale interval is  .
.
In what follows we assume the following:
-
(A1)
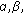 and
and  are positive constants with
are positive constants with 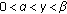 ;
; -
(A2)
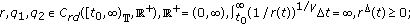
-
(A3)
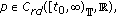 and
and 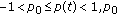 constant;
constant; -
(A4)
 for
for 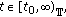 and
and 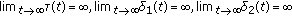 .
.
To develop the qualitative theory of delay dynamic equations on time scales, in this paper, by using the averaging technique and the generalized Riccati transformation, we consider the second-order nonlinear neutral delay dynamic equation on time scales (1.7) and establish several oscillation criteria. Our results in this paper not only extend the results given but also unify the oscillation of the second-order quasilinear delay differential equation and the second-order quasilinear delay difference equation. Applications to equations to which previously known criteria for oscillation are not applicable are given.
By a solution of (1.7), we mean a nontrivial real-valued function  ,
,  , which has the property
, which has the property  and satisfying (1.7) for
and satisfying (1.7) for  . Our attention is restricted to those solutions
. Our attention is restricted to those solutions  of (1.7) which exist on some half line
of (1.7) which exist on some half line  with
with  for any
for any  . A solution
. A solution  of (1.7) is called oscillatory if it is neither eventually positive nor eventually negative; otherwise it is called nonoscillatory. Equation (1.7) is called oscillatory if all solutions are oscillatory.
of (1.7) is called oscillatory if it is neither eventually positive nor eventually negative; otherwise it is called nonoscillatory. Equation (1.7) is called oscillatory if all solutions are oscillatory.
Equation (1.7) includes many other special important equations; for example, if  , (1.7) is the prototype of a wide class of nonlinear dynamic equations called Emden-Fowler neutral delay superlinear dynamic equation:
, (1.7) is the prototype of a wide class of nonlinear dynamic equations called Emden-Fowler neutral delay superlinear dynamic equation:

where  .
.
If  , (1.7) is the prototype of nonlinear dynamic equations called Emden-Fowler neutral delay sublinear dynamic equation:
, (1.7) is the prototype of nonlinear dynamic equations called Emden-Fowler neutral delay sublinear dynamic equation:

where  .
.
We note that if  , then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:
, then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:

If  , then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:
, then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:

If  , then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:
, then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:

If  , then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:
, then (1.7) becomes second-order nonlinear delay dynamic equation on time scales:

It is interesting to study (1.7) because the continuous version and its special cases have several physical applications, see [1] and when  is a discrete variable, and include its special cases also, are important in applications.
is a discrete variable, and include its special cases also, are important in applications.
The paper is organized as follows: In the next section we present the basic definitions and apply a simple consequence of Keller's chain rule, Young's inequality:

and the inequality

where  and
and  are nonnegative constants, devoted to the proof of the sufficient conditions for oscillation of all solutions of (1.7). In Section 3, we present some corollaries to illustrate our main results.
are nonnegative constants, devoted to the proof of the sufficient conditions for oscillation of all solutions of (1.7). In Section 3, we present some corollaries to illustrate our main results.
2. Main Results
In this section we shall give some oscillation criteria for (1.7) under the cases when  and
and  . It will be convenient to make the following notations in the remainder of this paper. Define
. It will be convenient to make the following notations in the remainder of this paper. Define

We define the function space  as follows:
as follows:  provided that
provided that  is defined for
is defined for  and
and  is rd-continuous function and nonnegative. For given function
is rd-continuous function and nonnegative. For given function  , we set
, we set

In order to prove our main results, we will use the formula

where  is delta differentiable and eventually positive or eventually negative, which is a simple consequence of Keller's chain rule (see Bohner and Peterson [2, Theorem
is delta differentiable and eventually positive or eventually negative, which is a simple consequence of Keller's chain rule (see Bohner and Peterson [2, Theorem  ]).
]).
Also, we assume the condition 
 and
and  , and there exists
, and there exists  such that
such that  and
and 
Lemma 2.1.
Assume  . If
. If  is an eventually positive solution of (1.7), then, there exists a
is an eventually positive solution of (1.7), then, there exists a  such that
such that  for
for  . Moreover,
. Moreover,

Lemma 2.2.
Assume  ,
,

If  is an eventually positive solution of (1.7), then
is an eventually positive solution of (1.7), then

The proof of Lemmas 2.1 and 2.2 is similar to that of Saker et al. [39, Lemma  ]; so it is omitted.
]; so it is omitted.
Lemma 2.3.
Assume that the condition  holds:
holds:

If  is an eventually positive solution of (1.7), then
is an eventually positive solution of (1.7), then


or  .
.
Proof.
Since  is an eventually positive solution of (1.7), there exists a number
is an eventually positive solution of (1.7), there exists a number  such that
such that  ,
,  ,
,  and
and  for all
for all  . In view of (1.7), we have
. In view of (1.7), we have

By  , then
, then  , we get
, we get

Let  , then (2.8) holds, and
, then (2.8) holds, and  is an eventually decreasing function. It follows that
is an eventually decreasing function. It follows that

We prove that  is eventually positive.
is eventually positive.
Otherwise, there exists a  such that
such that  , then we have
, then we have  for
for  , and hence
, and hence  which implies that
which implies that

Therefore, there exists  and
and  such that
such that

We can choose some positive integer  such that
such that  for
for  Thus, we obtain
Thus, we obtain

The above inequality implies that  for sufficiently large
for sufficiently large  which contradicts the fact that
which contradicts the fact that  eventually. Hence
eventually. Hence  eventually. Consequently, there are two possible cases:
eventually. Consequently, there are two possible cases:
-
(i)
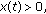 eventually;
eventually; -
(ii)
 eventually.
eventually.
If Case  holds, we can get
holds, we can get

Actually, by 
 , we can easily verify that
, we can easily verify that  Using (2.3), we get
Using (2.3), we get

From  , we have that
, we have that  is eventually negative.
is eventually negative.
Let  since
since  is eventually positive, so
is eventually positive, so  is eventually increasing. Therefore,
is eventually increasing. Therefore,  is either eventually positive or eventually negative. If
is either eventually positive or eventually negative. If  is eventually negative, then there is a
is eventually negative, then there is a  such that
such that  for
for  . So,
. So,

which implies that  is strictly increasing for
is strictly increasing for  . Pick
. Pick  so that
so that  for
for  . Then
. Then

so that  for
for  .
.
By (2.8), we have

which implies that

which contradicts (2.7). Hence, without loss of generality, there is a  such that
such that  , that is,
, that is,  for
for  . Consequently,
. Consequently,

and we have that  is strictly decreasing for
is strictly decreasing for  .
.
If there exists a  such that Case
such that Case  holds, then
holds, then  exists,
exists,  and we claim that
and we claim that  Otherwise,
Otherwise,  We can choose some positive integer
We can choose some positive integer  such that
such that  for
for  Thus, we obtain
Thus, we obtain

which implies that  and
and  which contradicts
which contradicts 
Now, we assert that  is bounded. If it is not true, there exists
is bounded. If it is not true, there exists  with
with  as
as  such that
such that

From  and
and

which implies that  it contradicts the existence of
it contradicts the existence of  Therefore, we can assume that
Therefore, we can assume that

By  we get
we get

thus  and
and  Hence,
Hence,  The proof is complete.
The proof is complete.
Theorem 2.4.
Assume that (2.5) holds,  ,
,

Then (1.7) is oscillatory on  .
.
Proof.
Suppose that (1.7) has a nonoscillatory solution  . We may assume that
. We may assume that  is eventually positive. We shall consider only this case, since the proof when
is eventually positive. We shall consider only this case, since the proof when  is eventually negative is similar. In view of Lemmas 2.1 and 2.2, there exists a
is eventually negative is similar. In view of Lemmas 2.1 and 2.2, there exists a  such that
such that  , and
, and  for
for  .
.
From (2.4) we have for 

and hence

So,

So,

Now note that  imply
imply

This contradicts (2.28). The proof is complete.
Remark 2.5.
Theorem 2.4 includes results of Agarwal et al. [21, Theorem  ] and Han et al. [25, Theorem
] and Han et al. [25, Theorem  ].
].
Theorem 2.6.
Assume that the condition  and (2.7) hold:
and (2.7) hold:

Then every solution of (1.7) either oscillates or tends to zero as  .
.
Proof.
Suppose that (1.7) has a nonoscillatory solution  . We may assume that
. We may assume that  is eventually positive. In view of Lemma 2.3, either
is eventually positive. In view of Lemma 2.3, either  or there exists a
or there exists a  such that
such that  and
and  is strictly decreasing for
is strictly decreasing for  .
.
Then from (2.8), we have for 

Since the rest of the proof is similar to Theorem 2.4, so we omit the detail. The proof is complete.
Theorem 2.7.
Assume that (2.5) holds.  , let
, let  ,
,

then (1.7) is oscillatory on  , where
, where  .
.
Proof.
Suppose that (1.7) has a nonoscillatory solution  . We may assume that
. We may assume that  is eventually positive. In view of Lemmas 2.1 and 2.2, there exists a
is eventually positive. In view of Lemmas 2.1 and 2.2, there exists a  such that
such that  , and
, and  for
for  . Define the function
. Define the function  by
by

We get

If  , by (2.3), we get
, by (2.3), we get

So, from (2.4) we have

By Young's inequality (1.14), we obtain that

From  being strictly decreasing,
being strictly decreasing,  , by (2.37) and (2.40), we get that
, by (2.37) and (2.40), we get that

that is,

So,

Using the inequality (1.15) we have

Integrating the inequality above from  to
to  we obtain
we obtain

Therefore,

which contradicts (2.36).
If  , proceeding as the proof of above, we have (2.37) and (2.38). By (2.3), we get that
, proceeding as the proof of above, we have (2.37) and (2.38). By (2.3), we get that

So, from (2.4) we have

Since the rest of the proof is similar to that of above, so we omit the detail. The proof is complete.
Theorem 2.8.
Assume that the condition  and (2.7) hold, let
and (2.7) hold, let  ,
,

then every solution of (1.7) either oscillates or tends to zero as  , where
, where  .
.
Proof.
Suppose that (1.7) has a nonoscillatory solution  . We may assume that
. We may assume that  is eventually positive. In view of Lemma 2.3, either
is eventually positive. In view of Lemma 2.3, either  or there exists a
or there exists a  such that
such that  and
and  for
for  .
.
Since the rest of the proof is similar to Theorem 2.7, so we omit the detail. The proof is complete.
Theorem 2.9.
Assume that (2.5) holds.  , let
, let  ,
,

then (1.7) is oscillatory on  .
.
Proof.
We prove only case  . The proof of case
. The proof of case  is similar. Proceeding as the proof of Theorem 2.7, we have (2.37) and (2.43). Replacing
is similar. Proceeding as the proof of Theorem 2.7, we have (2.37) and (2.43). Replacing  in (2.43) by
in (2.43) by  , then multiplying (2.43) by
, then multiplying (2.43) by  , and integrating from
, and integrating from  to
to  ,
,  , we have
, we have

Integrating by parts and using the fact that  , we get
, we get

So,

that is,

Hence,

Using the inequality (1.15) we have

Set  , so,
, so,

This contradicts (2.51) and finishes the proof.
Theorem 2.10.
Assume that the condition  and (2.7) hold, let
and (2.7) hold, let  ,
,

then every solution of (1.7) either oscillates or tends to zero as  .
.
Proof.
Suppose that (1.7) has a nonoscillatory solution  . We may assume that
. We may assume that  is eventually positive. In view of Lemma 2.3, either
is eventually positive. In view of Lemma 2.3, either  or there exists a
or there exists a  such that
such that  and
and  for
for  .
.
Since the rest of the proof is similar to Theorem 2.9, so we omit the detail. The proof is complete.
Following the procedure of the proof of Theorem 2.7, we can also prove the following theorem.
Theorem 2.11.
Assume that (2.5) holds.  , let
, let  ,
,


there exists  such that
such that

or

and for any  ,
,

and then (1.7) is oscillatory on  , where
, where  .
.
Proof.
We prove only case  . The proof of case
. The proof of case  is similar. Proceeding as the proof of Theorem 2.9, we have (2.56) and (2.57). So we have for all
is similar. Proceeding as the proof of Theorem 2.9, we have (2.56) and (2.57). So we have for all  ,
,

By (2.64), we obtain

Define

Then, by (2.56) and (2.64), we have that

We claim that

Suppose, to the contrary, that

By (2.60), there exists a positive constant  such that
such that

Let  be an arbitrary positive number, then it follows from (2.70) that there exists a
be an arbitrary positive number, then it follows from (2.70) that there exists a  such that
such that

Hence,

By (2.71), there exists a  such that
such that  , which implies that
, which implies that  . Since
. Since  is arbitrary, then
is arbitrary, then

In view of (2.68), we consider a sequence  with
with  satisfying
satisfying

Then, there exists a constant  such that
such that  for all sufficiently large
for all sufficiently large  . Since (2.70) ensures that
. Since (2.70) ensures that

so,

hold for all sufficiently large  . Therefore,
. Therefore,

On the other hand, from the definition of  we can obtain, by Hölder's inequality,
we can obtain, by Hölder's inequality,

and, accordingly,

So, because of (2.78), we get

which gives that

contradicting (2.61). Hence, (2.69) holds. In view of (2.66), from (2.69), we have

which contradicts (2.62). The proof is complete.
Theorem 2.12.
Assume that the condition  and (2.7) hold, let
and (2.7) hold, let  , there exists
, there exists  such that (2.60) and (2.61), and either (2.62) or (2.63) hold, and for any
such that (2.60) and (2.61), and either (2.62) or (2.63) hold, and for any  ,
,

and then every solution of (1.7) either oscillates or tends to zero as  .
.
Proof.
Suppose that (1.7) has a nonoscillatory solution  . We may assume that
. We may assume that  is eventually positive. In view of Lemma 2.3, either
is eventually positive. In view of Lemma 2.3, either  or there exists a
or there exists a  such that
such that  and
and  for
for  .
.
Since the rest of the proof is similar to Theorem 2.11, so we omit the detail. The proof is complete.
Following the procedure of the proof of Theorem 2.8, we can also prove the following theorem.
Theorem 2.13.
Assume that (2.5) and (2.60) hold,  , let
, let  ,
,

there exists  such that (2.62) or (2.63) holds, and for any
such that (2.62) or (2.63) holds, and for any  ,
,

and then (1.7) is oscillatory on  .
.
Theorem 2.14.
Assume that the condition  , (2.7), and (2.60) hold, let
, (2.7), and (2.60) hold, let  , there exists
, there exists  such that (2.62) or (2.63) holds, and for any
such that (2.62) or (2.63) holds, and for any  ,
,

and then every solution of (1.7) either oscillates or tends to zero as  .
.
Remark 2.15.
As Theorem 2.7–Theorem 2.14 are rather general, it is convenient for applications to derive a number of oscillation criteria with the appropriate choice of the functions  and
and  .
.
3. Examples
In this section, we give some examples to illustrate our main results.
Example 3.1.
Consider the following delay dynamic equations on time scales:

where

with  ,
,  for
for  and
and  . Then, by Theorem 2.4, we have
. Then, by Theorem 2.4, we have

Then (3.1) is oscillatory on  .
.
Example 3.2.
Consider the second-order delay dynamic equations on time scales:

where

with  ,
,  for
for  and
and  . Then,
. Then,

let  , and by Theorem 2.7, we have
, and by Theorem 2.7, we have

Then (3.4) is oscillatory on  .
.
References
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Anderson DR: Interval criteria for oscillation of nonlinear second-order dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4614-4623. 10.1016/j.na.2007.11.017
Bohner M, Saker SH: Oscillation of second order nonlinear dynamic equations on time scales. The Rocky Mountain Journal of Mathematics 2004,34(4):1239-1254. 10.1216/rmjm/1181069797
Akin-Bohner E, Hoffacker J: Oscillation properties of an Emden-Fowler type equation on discrete time scales. Journal of Difference Equations and Applications 2003,9(6):603-612. 10.1080/1023619021000053575
Akin-Bohner E, Bohner M, Saker SH: Oscillation criteria for a certain class of second order Emden-Fowler dynamic equations. Electronic Transactions on Numerical Analysis 2007, 27: 1-12.
Erbe L: Oscillation results for second-order linear equations on a time scale. Journal of Difference Equations and Applications 2002,8(11):1061-1071. 10.1080/10236190290015317
Erbe L, Peterson A, Saker SH: Oscillation criteria for second-order nonlinear dynamic equations on time scales. Journal of the London Mathematical Society 2003,67(3):701-714. 10.1112/S0024610703004228
Erbe L, Hassan TS, Peterson A: Oscillation criteria for nonlinear damped dynamic equations on time scales. Applied Mathematics and Computation 2008,203(1):343-357. 10.1016/j.amc.2008.04.038
Erbe L, Baoguo J, Peterson A: Nonoscillation for second order sublinear dynamic equations on time scales. Journal of Computational and Applied Mathematics 2009,232(2):594-599. 10.1016/j.cam.2009.06.039
Grace SR, Agarwal RP, Kaymakçalan B, Wichuta S: On the oscillation of certain second order nonlinear dynamic equations. Mathematical and Computer Modelling 2009,50(1-2):273-286. 10.1016/j.mcm.2008.12.007
Grace SR, Agarwal RP, Bohner M, O'Regan D: Oscillation of second-order strongly superlinear and strongly sublinear dynamic equations. Communications in Nonlinear Science and Numerical Simulation 2009,14(8):3463-3471. 10.1016/j.cnsns.2009.01.003
Hassan TS: Oscillation criteria for half-linear dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2008,345(1):176-185. 10.1016/j.jmaa.2008.04.019
Hassan TS: Oscillation of third order nonlinear delay dynamic equations on time scales. Mathematical and Computer Modelling 2009,49(7-8):1573-1586. 10.1016/j.mcm.2008.12.011
Jia B, Erbe L, Peterson A: New comparison and oscillation theorems for second-order half-linear dynamic equations on time scales. Computers & Mathematics with Applications 2008,56(10):2744-2756. 10.1016/j.camwa.2008.05.014
Li T, Han Z, Sun S, Zhang C: Forced oscillation of second-order nonlinear dynamic equations on time scales. Electronic Journal of Qualitative Theory of Differential Equations 2009, 60: 1-8.
Saker SH: Oscillation of nonlinear dynamic equations on time scales. Applied Mathematics and Computation 2004,148(1):81-91. 10.1016/S0096-3003(02)00829-9
Saker SH: Oscillation criteria of second-order half-linear dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,177(2):375-387. 10.1016/j.cam.2004.09.028
Yu Z-H, Wang Q-R: Asymptotic behavior of solutions of third-order nonlinear dynamic equations on time scales. Journal of Computational and Applied Mathematics 2009,225(2):531-540. 10.1016/j.cam.2008.08.017
Agarwal RP, Bohner M, Saker SH: Oscillation of second order delay dynamic equations. The Canadian Applied Mathematics Quarterly 2005,13(1):1-18.
Anderson DR: Oscillation of second-order forced functional dynamic equations with oscillatory potentials. Journal of Difference Equations and Applications 2007,13(5):407-421. 10.1080/10236190601116209
Bohner M: Some oscillation criteria for first order delay dynamic equations. Far East Journal of Applied Mathematics 2005,18(3):289-304.
Erbe L, Peterson A, Saker SH: Oscillation criteria for second-order nonlinear delay dynamic equations. Journal of Mathematical Analysis and Applications 2007,333(1):505-522. 10.1016/j.jmaa.2006.10.055
Han Z, Sun S, Shi B: Oscillation criteria for a class of second-order Emden-Fowler delay dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2007,334(2):847-858. 10.1016/j.jmaa.2007.01.004
Han Z, Shi B, Sun S: Oscillation criteria for second-order delay dynamic equations on time scales. Advances in Difference Equations 2007, 2007:-16.
Han ZL, Shi B, Sun SR: Oscillation of second-order delay dynamic equations on time scales. Acta Scientiarum Naturalium Universitatis Sunyatseni 2007,46(6):10-13.
Han Z, Li T, Sun S, Zhang C: Oscillation for second-order nonlinear delay dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-13.
Şahiner Y: Oscillation of second-order delay differential equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2005,63(5–7):e1073-e1080.
Sun S, Han Z, Zhang C: Oscillation of second-order delay dynamic equations on time scales. Journal of Applied Mathematics and Computing 2009,30(1-2):459-468. 10.1007/s12190-008-0185-6
Zhang BG, Deng X: Oscillation of delay differential equations on time scales. Mathematical and Computer Modelling 2002,36(11–13):1307-1318. 10.1016/S0895-7177(02)00278-9
Zhang BG, Shanliang Z: Oscillation of second-order nonlinear delay dynamic equations on time scales. Computers & Mathematics with Applications 2005,49(4):599-609. 10.1016/j.camwa.2004.04.038
Agarwal RP, O'Regan D, Saker SH: Oscillation criteria for second-order nonlinear neutral delay dynamic equations. Journal of Mathematical Analysis and Applications 2004,300(1):203-217. 10.1016/j.jmaa.2004.06.041
Han Z, Li T, Sun S, Zhang C: Oscillation behavior of third order neutral Emden-Fowler delay dynamic equations on time scales. Advances in Difference Equations 2010, 2010:-23.
Agwo HA: Oscillation of nonlinear second order neutral delay dynamic equations on time scales. Bulletin of the Korean Mathematical Society 2008,45(2):299-312. 10.4134/BKMS.2008.45.2.299
Li T, Han Z, Sun S, Yang D: Existence of nonoscillatory solutions to second-order neutral delay dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-10.
Saker SH: Oscillation of second-order nonlinear neutral delay dynamic equations on time scales. Journal of Computational and Applied Mathematics 2006,187(2):123-141. 10.1016/j.cam.2005.03.039
Saker SH, Agarwal RP, O'Regan D: Oscillation results for second-order nonlinear neutral delay dynamic equations on time scales. Applicable Analysis 2007,86(1):1-17. 10.1081/00036810601091630
Saker SH, O'Regan D, Agarwal RP: Oscillation theorems for second-order nonlinear neutral delay dynamic equations on time scales. Acta Mathematica Sinica 2008,24(9):1409-1432. 10.1007/s10114-008-7090-7
Şahíner Y: Oscillation of second-order neutral delay and mixed-type dynamic equations on time scales. Advances in Difference Equations 2006, 2006:-9.
Sun Y, Han Z, Li T, Zhang G: Oscillation criteria for second order quasi-linear neutral delay dynamic equations on time scales. Advances in Difference Equations. In press
Tripathy AK: Some oscillation results for second order nonlinear dynamic equations of neutral type. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):e1727-e1735. 10.1016/j.na.2009.02.046
Wu H-W, Zhuang R-K, Mathsen RM: Oscillation criteria for second-order nonlinear neutral variable delay dynamic equations. Applied Mathematics and Computation 2006,178(2):321-331. 10.1016/j.amc.2005.11.049
Zhu Z-Q, Wang Q-R: Existence of nonoscillatory solutions to neutral dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2007,335(2):751-762. 10.1016/j.jmaa.2007.02.008
Acknowledgments
This research is supported by the Natural Science Foundation of China (60774004, 60904024), China Postdoctoral Science Foundation funded project (20080441126, 200902564), Shandong Postdoctoral funded project (200802018), the Natural Science Foundation of Shandong (Y2008A28, ZR2009AL003), and also supported by University of Jinan Research Funds for Doctors (B0621, XBS0843).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Han, Z., Sun, S., Li, T. et al. Oscillatory Behavior of Quasilinear Neutral Delay Dynamic Equations on Time Scales. Adv Differ Equ 2010, 450264 (2010). https://doi.org/10.1155/2010/450264
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/450264
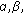 and
and  are positive constants with
are positive constants with 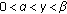 ;
;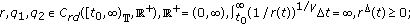
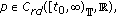 and
and 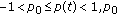 constant;
constant; for
for 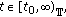 and
and 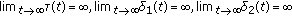 .
.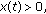 eventually;
eventually; eventually.
eventually.