- Research Article
- Open access
- Published:
Exponential Decay of Energy for Some Nonlinear Hyperbolic Equations with Strong Dissipation
Advances in Difference Equations volume 2010, Article number: 357404 (2010)
Abstract
The initial boundary value problem for a class of hyperbolic equations with strong dissipative term  in a bounded domain is studied. The existence of global solutions for this problem is proved by constructing a stable set in
in a bounded domain is studied. The existence of global solutions for this problem is proved by constructing a stable set in  and showing the exponential decay of the energy of global solutions through the use of an important lemma of V. Komornik.
and showing the exponential decay of the energy of global solutions through the use of an important lemma of V. Komornik.
1. Introduction
We are concerned with the global solvability and exponential asymptotic stability for the following hyperbolic equation in a bounded domain:

with initial conditions

and boundary condition

where  is a bounded domain in
is a bounded domain in  with a smooth boundary
with a smooth boundary  ,
,  and
and  are real numbers, and
are real numbers, and  is a divergence operator (degenerate Laplace operator) with
is a divergence operator (degenerate Laplace operator) with  , which is called a
, which is called a  -Laplace operator.
-Laplace operator.
Equations of type (1.1) are used to describe longitudinal motion in viscoelasticity mechanics and can also be seen as field equations governing the longitudinal motion of a viscoelastic configuration obeying the nonlinear Voight model [1–4].
For  , it is well known that the damping term assures global existence and decay of the solution energy for arbitrary initial data [4–6]. For
, it is well known that the damping term assures global existence and decay of the solution energy for arbitrary initial data [4–6]. For  , the source term causes finite time blow up of solutions with negative initial energy if
, the source term causes finite time blow up of solutions with negative initial energy if  [7].
[7].
In [8–10], Yang studied the problem (1.1)–(1.3) and obtained global existence results under the growth assumptions on the nonlinear terms and initial data. These global existence results have been improved by Liu and Zhao [11] by using a new method. As for the nonexistence of global solutions, Yang [12] obtained the blow up properties for the problem (1.1)–(1.3) with the following restriction on the initial energy  , where
, where  and
and  , and
, and  are some positive constants.
are some positive constants.
Because the  -Laplace operator
-Laplace operator  is nonlinear operator, the reasoning of proof and computation are greatly different from the Laplace operator
is nonlinear operator, the reasoning of proof and computation are greatly different from the Laplace operator  . By means of the Galerkin method and compactness criteria and a difference inequality introduced by Nakao [13], Ye [14, 15] has proved the existence and decay estimate of global solutions for the problem (1.1)–(1.3) with inhomogeneous term
. By means of the Galerkin method and compactness criteria and a difference inequality introduced by Nakao [13], Ye [14, 15] has proved the existence and decay estimate of global solutions for the problem (1.1)–(1.3) with inhomogeneous term  and
and  .
.
In this paper we are going to investigate the global existence for the problem (1.1)–(1.3) by applying the potential well theory introduced by Sattinger [16], and we show the exponential asymptotic behavior of global solutions through the use of the lemma of Komornik [17].
We adopt the usual notation and convention. Let  denote the Sobolev space with the norm
denote the Sobolev space with the norm  and
and  denote the closure in
denote the closure in  of
of  . For simplicity of notation, hereafter we denote by
. For simplicity of notation, hereafter we denote by  the Lebesgue space
the Lebesgue space  norm,
norm,  denotes
denotes  norm, and write equivalent norm
norm, and write equivalent norm  instead of
instead of  norm
norm  . Moreover,
. Moreover,  denotes various positive constants depending on the known constants, and it may be different at each appearance.
denotes various positive constants depending on the known constants, and it may be different at each appearance.
2. The Global Existence and Nonexistence
In order to state and study our main results, we first define the following functionals:

for  . Then we define the stable set
. Then we define the stable set  by
by

where

We denote the total energy associated with (1.1)–(1.3) by

for  ,
,  , and
, and  is the total energy of the initial data.
is the total energy of the initial data.
Definition 2.1.
The solution  is called the weak solution of the problem (1.1)–(1.3) on
is called the weak solution of the problem (1.1)–(1.3) on  , if
, if  satisfy
satisfy

 and
and  in
in  ,
,  in
in  .
.
We need the following local existence result, which is known as a standard one (see [14, 18, 19]).
Theorem 2.2.
Suppose that  if
if  and
and  if
if  . If
. If  , then there exists
, then there exists  such that the problem (1.1)–(1.3) has a unique local solution
such that the problem (1.1)–(1.3) has a unique local solution  in the class
in the class

For latter applications, we list up some lemmas.
Let  , then
, then  , and the inequality
, and the inequality  holds with a constant
holds with a constant  depending on
depending on  , and
, and  , provided that,
, provided that,  if
if  and
and  .
.
Lemma 2.4.
Let  be a solution to problem (1.1)–(1.3). Then
be a solution to problem (1.1)–(1.3). Then  is a nonincreasing function for
is a nonincreasing function for  and
and

Proof.
By multiplying (1.1) by  and integrating over
and integrating over  , we get
, we get

which implies from (2.4) that

Therefore,  is a nonincreasing function on
is a nonincreasing function on  .
.
Lemma 2.5.
Let  ; if the hypotheses in Theorem 2.2 hold, then
; if the hypotheses in Theorem 2.2 hold, then  .
.
Proof.
Since

so, we get

Let  , which implies that
, which implies that

As  , an elementary calculation shows that
, an elementary calculation shows that

Hence, we have from Lemma 2.3 that

We get from the definition of  that
that 
Lemma 2.6.
Let  , then
, then

Proof.
By the definition of  and
and  , we have the following identity:
, we have the following identity:

Since  , so we have
, so we have  . Therefore, we obtain from (2.16) that
. Therefore, we obtain from (2.16) that

In order to prove the existence of global solutions for the problem (1.1)-(1.3), we need the following lemma.
Lemma 2.7.
Suppose that  if
if  and
and  if
if  . If
. If  , and
, and  , then
, then  , for each
, for each  .
.
Proof.
Assume that there exists a number  such that
such that  on
on  and
and  . Then, in virtue of the continuity of
. Then, in virtue of the continuity of  , we see that
, we see that  . From the definition of
. From the definition of  and the continuity of
and the continuity of  and
and  in
in  , we have either
, we have either

or

It follows from (2.4) that

So, case (2.18) is impossible.
Assume that (2.19) holds, then we get that

We obtain from  that
that  .
.
Since

consequently, we get from (2.20) that

which contradicts the definition of  . Therefore, case (2.19) is impossible as well. Thus, we conclude that
. Therefore, case (2.19) is impossible as well. Thus, we conclude that  on
on  .
.
Theorem 2.8.
Assume that  if
if  and
and  if
if  .
.  is a local solution of problem (1.1)–(1.3) on
is a local solution of problem (1.1)–(1.3) on  . If
. If  , and
, and  , then the solution
, then the solution  is a global solution of the problem (1.1)–(1.3).
is a global solution of the problem (1.1)–(1.3).
Proof.
It suffices to show that  is bounded independently of
is bounded independently of  .
.
Under the hypotheses in Theorem 2.8, we get from Lemma 2.7 that  on
on  . So formula (2.15) in Lemma 2.6 holds on
. So formula (2.15) in Lemma 2.6 holds on  . Therefore, we have from (2.15) and Lemma 2.4 that
. Therefore, we have from (2.15) and Lemma 2.4 that

Hence, we get

The above inequality and the continuation principle lead to the global existence of the solution, that is,  . Thus, the solution
. Thus, the solution  is a global solution of the problem (1.1)–(1.3).
is a global solution of the problem (1.1)–(1.3).
Now we employ the analysis method to discuss the blow-up solutions of the problem (1.1)–(1.3) in finite time. Our result reads as follows.
Theorem 2.9.
Suppose that  if
if  and
and  if
if  . If
. If  , assume that the initial value is such that
, assume that the initial value is such that

where

with  is a positive Sobolev constant. Then the solution of the problem (1.1)–(1.3) does not exist globally in time.
is a positive Sobolev constant. Then the solution of the problem (1.1)–(1.3) does not exist globally in time.
Proof.
On the contrary, under the conditions in Theorem 2.9, let  be a global solution of the problem (1.1)–(1.3); then by Lemma 2.3, it is well known that there exists a constant
be a global solution of the problem (1.1)–(1.3); then by Lemma 2.3, it is well known that there exists a constant  depending only on
depending only on  , and
, and  such that
such that  for all
for all  .
.
From the above inequality, we conclude that

By using (2.28), it follows from the definition of  that
that

Setting

we denote the right side of (2.29) by  , then
, then

We have

Letting  , we obtain
, we obtain  .
.
As  , we have
, we have

Consequently, the function  has a single maximum value
has a single maximum value  at
at  , where
, where

Since the initial data is such that  satisfies
satisfies

Therefore, from Lemma 2.4 we get

At the same time, by (2.29) and (2.31), it is clear that there can be no time  for which
for which

Hence we have also  for all
for all  from the continuity of
from the continuity of  and
and  .
.
According to the above contradiction, we know that the global solution of the problem (1.1)–(1.3) does not exist, that is, the solution blows up in some finite time.
This completes the proof of Theorem 2.9.
3. The Exponential Asymptotic Behavior
Lemma 3.1 (see [17]).
Let  be a nonincreasing function, and assume that there is a constant
be a nonincreasing function, and assume that there is a constant  such that
such that

then  , for all
, for all  .
.
The following theorem shows the exponential asymptotic behavior of global solutions of problem (1.1)–(1.3).
Theorem 3.2.
If the hypotheses in Theorem 2.8 are valid, then the global solutions of problem (1.1)–(1.3) have the following exponential asymptotic behavior:

Proof.
Multiplying by  on both sides of (1.1) and integrating over
on both sides of (1.1) and integrating over  gives
gives

where  .
.
Since

so, substituting the formula (3.4) into the right-hand side of (3.3) gives

By exploiting Lemma 2.3 and (2.24), we easily arrive at

We obtain from (3.6) and (2.24) that

It follows from (3.7) and (3.5) that

We have from Hölder inequality, Lemma 2.3 and (2.24) that

Substituting the estimates of (3.9) into (3.8), we conclude that

We get from Lemma 2.3 and Lemma 2.4 that

From Young inequality, Lemmas 2.3 and 2.4, and (2.24), it follows that

Choosing  small enough, such that
small enough, such that

and, substituting (3.11) and (3.12) into (3.10), we get

We let  in (3.14) to get
in (3.14) to get

Therefore, we have from (3.15) and Lemma 3.1 that

We conclude from  , (2.4) and (3.16) that
, (2.4) and (3.16) that

The proof of Theorem 3.2 is thus finished.
References
Andrews G:On the existence of solutions to the equation
 . Journal of Differential Equations 1980,35(2):200-231. 10.1016/0022-0396(80)90040-6
. Journal of Differential Equations 1980,35(2):200-231. 10.1016/0022-0396(80)90040-6Andrews G, Ball JM: Asymptotic behaviour and changes of phase in one-dimensional nonlinear viscoelasticity. Journal of Differential Equations 1982,44(2):306-341. 10.1016/0022-0396(82)90019-5
Ang DD, Dinh PN: Strong solutions of quasilinear wave equation with non-linear damping. SIAM Journal on Mathematical Analysis 1985, 19: 337-347. 10.1137/0519024
Kawashima S, Shibata Y: Global existence and exponential stability of small solutions to nonlinear viscoelasticity. Communications in Mathematical Physics 1992,148(1):189-208. 10.1007/BF02102372
Haraux A, Zuazua E: Decay estimates for some semilinear damped hyperbolic problems. Archive for Rational Mechanics and Analysis 1988,100(2):191-206. 10.1007/BF00282203
Kopáčková M: Remarks on bounded solutions of a semilinear dissipative hyperbolic equation. Commentationes Mathematicae Universitatis Carolinae 1989,30(4):713-719.
Ball JM: Remarks on blow-up and nonexistence theorems for nonlinear evolution equations. The Quarterly Journal of Mathematics. Oxford 1977,28(112):473-486. 10.1093/qmath/28.4.473
Yang Z: Existence and asymptotic behaviour of solutions for a class of quasi-linear evolution equations with non-linear damping and source terms. Mathematical Methods in the Applied Sciences 2002,25(10):795-814. 10.1002/mma.306
Yang Z, Chen G: Global existence of solutions for quasi-linear wave equations with viscous damping. Journal of Mathematical Analysis and Applications 2003,285(2):604-618. 10.1016/S0022-247X(03)00448-7
Zhijian Y: Initial boundary value problem for a class of non-linear strongly damped wave equations. Mathematical Methods in the Applied Sciences 2003,26(12):1047-1066. 10.1002/mma.412
Yacheng L, Junsheng Z: Multidimensional viscoelasticity equations with nonlinear damping and source terms. Nonlinear Analysis: Theory, Methods & Applications 2004,56(6):851-865. 10.1016/j.na.2003.07.021
Yang Z: Blowup of solutions for a class of non-linear evolution equations with non-linear damping and source terms. Mathematical Methods in the Applied Sciences 2002,25(10):825-833. 10.1002/mma.312
Nakao M: A difference inequality and its application to nonlinear evolution equations. Journal of the Mathematical Society of Japan 1978,30(4):747-762. 10.2969/jmsj/03040747
Ye Y: Existence of global solutions for some nonlinear hyperbolic equation with a nonlinear dissipative term. Journal of Zhengzhou University 1997,29(3):18-23.
Ye Y: On the decay of solutions for some nonlinear dissipative hyperbolic equations. Acta Mathematicae Applicatae Sinica. English Series 2004,20(1):93-100. 10.1007/s10255-004-0152-4
Sattinger DH: On global solution of nonlinear hyperbolic equations. Archive for Rational Mechanics and Analysis 1968, 30: 148-172. 10.1007/BF00250942
Komornik V: Exact Controllability and Stabilization, Research in Applied Mathematics. Masson, Paris, France; 1994:viii+156.
Ye Y: Existence and nonexistence of global solutions of the initial-boundary value problem for some degenerate hyperbolic equation. Acta Mathematica Scientia 2005,25(4):703-709.
Gao H, Ma TF:Global solutions for a nonlinear wave equation with the
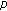 -Laplacian operator. Electronic Journal of Qualitative Theory of Differential Equations 1999, (11):1-13.
-Laplacian operator. Electronic Journal of Qualitative Theory of Differential Equations 1999, (11):1-13.Adams RA: Sobolev Spaces, Pure and Applied Mathematics. Volume 6. Academic Press, New York, NY, USA; 1975:xviii+268.
Ladyzhenskaya OA: The Boundary Value Problems of Mathematical Physics, Applied Mathematical Sciences. Volume 49. Springer, New York, NY, USA; 1985:xxx+322.
Acknowledgments
This paper was supported by the Natural Science Foundation of Zhejiang Province (no. Y6100016), the Science and Research Project of Zhejiang Province Education Commission (no. Y200803804 and Y200907298). The Research Foundation of Zhejiang University of Science and Technology (no. 200803), and the Middle-aged and Young Leader in Zhejiang University of Science and Technology (2008–2010).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ye, Y. Exponential Decay of Energy for Some Nonlinear Hyperbolic Equations with Strong Dissipation. Adv Differ Equ 2010, 357404 (2010). https://doi.org/10.1155/2010/357404
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/357404
 . Journal of Differential Equations 1980,35(2):200-231. 10.1016/0022-0396(80)90040-6
. Journal of Differential Equations 1980,35(2):200-231. 10.1016/0022-0396(80)90040-6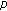 -Laplacian operator. Electronic Journal of Qualitative Theory of Differential Equations 1999, (11):1-13.
-Laplacian operator. Electronic Journal of Qualitative Theory of Differential Equations 1999, (11):1-13.