- Research Article
- Open access
- Published:
Existence of  Positive Periodic Solutions to
Positive Periodic Solutions to  -Species Nonautonomous Food Chains with Harvesting Terms
-Species Nonautonomous Food Chains with Harvesting Terms
Advances in Difference Equations volume 2010, Article number: 262461 (2010)
Abstract
By using Mawhin's continuation theorem of coincidence degree theory and some skills of inequalities, we establish the existence of at least  positive periodic solutions for
positive periodic solutions for  -species nonautonomous Lotka-Volterra type food chains with harvesting terms. An example is given to illustrate the effectiveness of our results.
-species nonautonomous Lotka-Volterra type food chains with harvesting terms. An example is given to illustrate the effectiveness of our results.
1. Introduction
The dynamic relationship between predators and their prey has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance. These problems may appear to be simple mathematically at first; sight, they are, in fact, very challenging and complicated. There are many different kinds of predator-prey models in the literature. For more details, we refer to [1, 2]. Food chain predator-prey system, as one of the most important predator-prey system, has been extensively studied by many scholars, many excellent results concerned with the persistent property and positive periodic solution of the system; see [3–13] and the references cited therein. However, to the best of the authors' knowledge, to this day, still no scholar study the  -species nonautonomous case of Food chain predator-prey system with harvesting terms. Indeed, the exploitation of biological resources and the harvest of population species are commonly practiced in fishery, forestry, and wildlife management; the study of population dynamics with harvesting is an important subject in mathematical bioeconomics, which is related to the optimal management of renewable resources (see [14–16]). This motivates us to consider the following
-species nonautonomous case of Food chain predator-prey system with harvesting terms. Indeed, the exploitation of biological resources and the harvest of population species are commonly practiced in fishery, forestry, and wildlife management; the study of population dynamics with harvesting is an important subject in mathematical bioeconomics, which is related to the optimal management of renewable resources (see [14–16]). This motivates us to consider the following  -species nonautonomous Lotka-Volterra type food chain model with harvesting terms:
-species nonautonomous Lotka-Volterra type food chain model with harvesting terms:

where  is the
is the  th species population density,
th species population density,  is the growth rate of the first species that is the only producer in system (1.1),
is the growth rate of the first species that is the only producer in system (1.1),  and
and  stand for the
stand for the  th species intraspecific competition rate and harvesting rate, respectively,
th species intraspecific competition rate and harvesting rate, respectively,  is the death rate of the
is the death rate of the  th species,
th species,  represents the
represents the  th species predation rate on the
th species predation rate on the  th species, and
th species, and  stands for the transformation rate from the
stands for the transformation rate from the  th species to the
th species to the  th species. In addition, the effects of a periodically varying environment are important for evolutionary theory as the selective forces on systems in a fluctuating environment differ from those in a stable environment. Therefore, the assumptions of periodicity of the parameters are a way of incorporating the periodicity of the environment (e.g, seasonal effects of weather, food supplies, mating habits, etc), which leads us to assume that
th species. In addition, the effects of a periodically varying environment are important for evolutionary theory as the selective forces on systems in a fluctuating environment differ from those in a stable environment. Therefore, the assumptions of periodicity of the parameters are a way of incorporating the periodicity of the environment (e.g, seasonal effects of weather, food supplies, mating habits, etc), which leads us to assume that  and
and  are all positive continuous
are all positive continuous  -periodic functions.
-periodic functions.
Since a very basic and important problem in the study of a population growth model with a periodic environment is the global existence and stability of a positive periodic solution, which plays a similar role as a globally stable equilibrium does in an autonomous model, this motivates us to investigate the existence of a positive periodic or multiple positive periodic solutions for system (1.1). In fact, it is more likely for some biological species to take on multiple periodic change regulations and have multiple local stable periodic phenomena. Therefore, it is essential for us to investigate the existence of multiple positive periodic solutions for population models. Our main purpose of this paper is by using Mawhin's continuation theorem of coincidence degree theory [17], to establish the existence of  positive periodic solutions for system (1.1). For the work concerning the multiple existence of periodic solutions of periodic population models which was done using coincidence degree theory, we refer to [18–21].
positive periodic solutions for system (1.1). For the work concerning the multiple existence of periodic solutions of periodic population models which was done using coincidence degree theory, we refer to [18–21].
The organization of the rest of this paper is as follows. In Section 2, by employing the continuation theorem of coincidence degree theory and the skills of inequalities, we establish the existence of at least  positive periodic solutions of system (1.1). In Section 3, an example is given to illustrate the effectiveness of our results.
positive periodic solutions of system (1.1). In Section 3, an example is given to illustrate the effectiveness of our results.
2. Existence of at Least 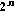 Positive Periodic Solutions
Positive Periodic Solutions
In this section, by using Mawhin's continuation theorem and the skills of inequalities, we shall show the existence of positive periodic solutions of (1.1). To do so, we need to make some preparations.
Let  and
and  be real normed vector spaces. Let
be real normed vector spaces. Let  be a linear mapping and
be a linear mapping and  be a continuous mapping. The mapping
be a continuous mapping. The mapping  will be called a Fredholm mapping of index zero if dim
will be called a Fredholm mapping of index zero if dim  and
and  is closed in
is closed in  . If
. If  is a Fredholm mapping of index zero, then there exist continuous projectors
is a Fredholm mapping of index zero, then there exist continuous projectors  and
and  such that
such that  and
and  and
and  It follows that
It follows that  is invertible and its inverse is denoted by
is invertible and its inverse is denoted by  . If
. If  is a bounded open subset of
is a bounded open subset of  , the mapping
, the mapping  is called
is called  -compact on
-compact on  , if
, if  is bounded and
is bounded and  is compact. Because Im
is compact. Because Im  is isomorphic to Ker
is isomorphic to Ker  , there exists an isomorphism
, there exists an isomorphism  .
.
The Mawhin's continuous theorem [17, page 40] is given as follows.
Lemma 2.1 (see [9]).
Let  be a Fredholm mapping of index zero and let
be a Fredholm mapping of index zero and let  be
be  -compact on
-compact on  . Assume that
. Assume that
-
(a)
for each
 , every solution
, every solution  of
of  is such that
is such that  ;
; -
(b)
 for each
for each 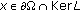 ;
; -
(c)
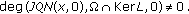
Then  has at least one solution in
has at least one solution in 
For the sake of convenience, we denote  respectively; here
respectively; here  is a continuous
is a continuous  -periodic function.
-periodic function.
For simplicity, we need to introduce some notations as follows:

where  .
.
Throughout this paper, we need the following assumptions:
 and
and 
()
Lemma 2.2.
Let  and
and  for the functions
for the functions  and
and  the following assertions hold:
the following assertions hold:
-
(1)
 and
and  are monotonically increasing and monotonically decreasing on the variable
are monotonically increasing and monotonically decreasing on the variable 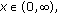 respectively.
respectively. -
(2)
 and
and  are monotonically decreasing and monotonically increasing on the variable
are monotonically decreasing and monotonically increasing on the variable 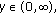 respectively.
respectively. -
(3)
 and
and  are monotonically decreasing and monotonically increasing on the variable
are monotonically decreasing and monotonically increasing on the variable  respectively.
respectively.
Proof.
In fact, for all  we have
we have

By the relationship of the derivative and the monotonicity, the above assertions obviously hold. The proof of Lemma 2.2 is complete.
Lemma 2.3.
Assume that  and
and  hold, then we have the following inequalities:
hold, then we have the following inequalities:

Proof.
Since

By assumptions  Lemma 2.2 and the expressions of
Lemma 2.2 and the expressions of  and
and  we have
we have

where  that is
that is  Thus, we have
Thus, we have  The proof of Lemma 2.3 is complete.
The proof of Lemma 2.3 is complete.
Theorem 2.4.
Assume that  and
and  hold. Then system (1.1) has at least
hold. Then system (1.1) has at least  positive
positive  -periodic solutions.
-periodic solutions.
Proof.
By making the substitution

system (1.1) can be reformulated as

where 
Let

and define

Equipped with the above norm  and
and  are Banach spaces. Let
are Banach spaces. Let

where  ,
,  We put
We put  Thus it follows that
Thus it follows that  is closed in
is closed in  and
and  are continuous projectors such that
are continuous projectors such that

Hence,  is a Fredholm mapping of index zero. Furthermore, the generalized inverse (to
is a Fredholm mapping of index zero. Furthermore, the generalized inverse (to  )
)  is given by
is given by

Then


where

Obviously,  and
and  are continuous. It is not difficult to show that
are continuous. It is not difficult to show that  is compact for any open bounded set
is compact for any open bounded set  by using the Arzela-Ascoli theorem. Moreover,
by using the Arzela-Ascoli theorem. Moreover,  is clearly bounded. Thus,
is clearly bounded. Thus,  is
is  -compact on
-compact on  with any open bounded set
with any open bounded set 
In order to use Lemma 2.1, we have to find at least  appropriate open bounded subsets of
appropriate open bounded subsets of  Corresponding to the operator equation
Corresponding to the operator equation  we have
we have

where  Assume that
Assume that  is an
is an  -periodic solution of system (2.16) for some
-periodic solution of system (2.16) for some  . Then there exist
. Then there exist  such that
such that  It is clear that
It is clear that  From this and (2.16), we have
From this and (2.16), we have


where 
On one hand, according to (2.17), we have

namely,

which implies that


that is,

which implies that

By deducing for  we obtain
we obtain

namely,

which implies that


namely,

which implies that

In view of (2.21), (2.24), (2.27), and (2.30), we have

From (2.18), one can analogously obtain

By (2.31) and (2.32), we get

On the other hand, in view of (2.17), we have

namely,

which implies that


that is,

which implies that

By deducing for  we obtain
we obtain

that is,

which implies that


namely,

which implies that

It follows from (2.36), (2.39), (2.42), and (2.45) that

From (2.18), one can analogously obtain

By (2.33), (2.46), (2.47), and Lemma 2.3, we get

which implies that, for all 

For convenience, we denote

Clearly,  and
and  are independent of
are independent of  For each
For each  , we choose an interval between two intervals
, we choose an interval between two intervals  and
and  , and denote it as
, and denote it as  , then define the set
, then define the set

Obviously, the number of the above sets is  We denote these sets as
We denote these sets as  are bounded open subsets of
are bounded open subsets of  Thus
Thus  satisfies the requirement
satisfies the requirement  in Lemma 2.1.
in Lemma 2.1.
Now we show that  of Lemma 2.1 holds; that is, we prove when
of Lemma 2.1 holds; that is, we prove when  If it is not true, then when
If it is not true, then when  constant vector
constant vector  with
with  , satisfies
, satisfies

where  In view of the mean value theorem of calculous, there exist
In view of the mean value theorem of calculous, there exist  points
points  such that
such that

where  Following the argument of (2.21)–(2.48), from (2.53), we obtain
Following the argument of (2.21)–(2.48), from (2.53), we obtain

Then  belongs to one of
belongs to one of  This contradicts the fact that
This contradicts the fact that  This proves that
This proves that  in Lemma 2.1 holds.
in Lemma 2.1 holds.
Finally, in order to show that  in Lemma 2.1 holds, we only prove that for
in Lemma 2.1 holds, we only prove that for  then it holds that
then it holds that  To this end, we define the mapping
To this end, we define the mapping  by
by

here  is a parameter and
is a parameter and  is defined by
is defined by

where  We show that for
We show that for  then it holds that
then it holds that  Otherwise, parameter
Otherwise, parameter  and constant vector
and constant vector  satisfy
satisfy  that is,
that is,

where  In view of the mean value theorem of calculous, there exist
In view of the mean value theorem of calculous, there exist  points
points  such that
such that

where  Following the argument of (2.21)–(2.48), from (2.58), we obtain
Following the argument of (2.21)–(2.48), from (2.58), we obtain

given that  belongs to one of
belongs to one of  This contradicts the fact that
This contradicts the fact that  This proves
This proves  holds. Note that the system of the following algebraic equations:
holds. Note that the system of the following algebraic equations:

has  distinct solutions since
distinct solutions since  and
and  hold,
hold,  where
where  or
or  Similar to the proof of Lemma 2.3, it is easy to verify that
Similar to the proof of Lemma 2.3, it is easy to verify that

Therefore,  uniquely belongs to the corresponding
uniquely belongs to the corresponding  Since
Since  we can take
we can take  A direct computation gives, for
A direct computation gives, for  ,
,

Since  then
then

So far, we have proved that  satisfies all the assumptions in Lemma 2.1. Hence, system (2.7) has at least
satisfies all the assumptions in Lemma 2.1. Hence, system (2.7) has at least  different
different  -periodic solutions. Thus, by (2.6) system (1.1) has at least
-periodic solutions. Thus, by (2.6) system (1.1) has at least  different positive
different positive  -periodic solutions. This completes the proof of Theorem 2.4.
-periodic solutions. This completes the proof of Theorem 2.4.
In system (1.1), if  and
and  are continuous periodic functions, then similar to the proof of Theorem 2.4, one can prove the following
are continuous periodic functions, then similar to the proof of Theorem 2.4, one can prove the following
Theorem 2.5.
Assume that  and
and  hold. Then system (1.1) has at least
hold. Then system (1.1) has at least  positive
positive  -periodic solutions.
-periodic solutions.
Remark 2.6.
In Theorem 2.5,  means that the
means that the  th species does not prey the
th species does not prey the  th species, thus
th species, thus  That is to say, there is no relationship between the
That is to say, there is no relationship between the  th species and the
th species and the  th species.
th species.
3. Illustrative Examples
Example 3.1.
Consider the following three-species food chain with harvesting terms:

In this case,  and
and  Since
Since

taking  then we have
then we have

Take  then
then

Take  then
then

Therefore, all conditions of Theorem 2.4 are satisfied. By Theorem 2.4, system (3.1) has at least eight positive  -periodic solutions.
-periodic solutions.
References
Berryman AA: The origins and evolution of predator-prey theory. Ecology 1992,73(5):1530-1535. 10.2307/1940005
Freedman HI: Deterministic Mathematical Models in Population Ecology, Monographs and Textbooks in Pure and Applied Mathematics. Volume 57. Marcel Dekker, New York, NY, USA; 1980:x+254.
Zhou S-R, Li W-T, Wang G: Persistence and global stability of positive periodic solutions of three species food chains with omnivory. Journal of Mathematical Analysis and Applications 2006,324(1):397-408. 10.1016/j.jmaa.2005.12.021
Sun YG, Saker SH: Positive periodic solutions of discrete three-level food-chain model of Holling type II. Applied Mathematics and Computation 2006,180(1):353-365. 10.1016/j.amc.2005.12.015
Li Y, Lu L, Zhu X:Existence of periodic solutions in
 -species food-chain system with impulsive. Nonlinear Analysis: Real World Applications 2006,7(3):414-431. 10.1016/j.nonrwa.2005.03.009
-species food-chain system with impulsive. Nonlinear Analysis: Real World Applications 2006,7(3):414-431. 10.1016/j.nonrwa.2005.03.009Zhang S, Tan D, Chen L: Dynamic complexities of a food chain model with impulsive perturbations and Beddington-DeAngelis functional response. Chaos, Solitons & Fractals 2006,27(3):768-777. 10.1016/j.chaos.2005.04.047
Xu R, Chen L, Hao F: Periodic solutions of a discrete time Lotka-Volterra type food-chain model with delays. Applied Mathematics and Computation 2005,171(1):91-103. 10.1016/j.amc.2005.01.027
Zhang S, Chen L: A Holling II functional response food chain model with impulsive perturbations. Chaos, Solitons & Fractals 2005,24(5):1269-1278. 10.1016/j.chaos.2004.09.051
Xu R, Chaplain MAJ, Davidson FA: Periodic solution for a three-species Lotka-Volterra food-chain model with time delays. Mathematical and Computer Modelling 2004,40(7-8):823-837. 10.1016/j.mcm.2004.10.011
Wang F, Hao C, Chen L: Bifurcation and chaos in a Monod-Haldene type food chain chemostat with pulsed input and washout. Chaos, Solitons & Fractals 2007,32(1):181-194. 10.1016/j.chaos.2005.10.083
Wang W, Wang H, Li Z: The dynamic complexity of a three-species Beddington-type food chain with impulsive control strategy. Chaos, Solitons & Fractals 2007,32(5):1772-1785. 10.1016/j.chaos.2005.12.025
Li Y, Lu L:Positive periodic solutions of discrete
 -species food-chain systems. Applied Mathematics and Computation 2005,167(1):324-344. 10.1016/j.amc.2004.06.082
-species food-chain systems. Applied Mathematics and Computation 2005,167(1):324-344. 10.1016/j.amc.2004.06.082Huo H-F, Li W-T: Existence and global stability of periodic solutions of a discrete ratio-dependent food chain model with delay. Applied Mathematics and Computation 2005,162(3):1333-1349. 10.1016/j.amc.2004.03.013
Clark CW: Mathematical Bioeconomics: The Optimal Management of Renewable Resources, Pure and Applied Mathematics. 2nd edition. John Wiley & Sons, New York, NY, USA; 1990:xiv+386.
Troutman JL: Variational Calculus and Optimal Control, Undergraduate Texts in Mathematics. 2nd edition. Springer, New York, NY, USA; 1996:xvi+461.
Leung AW: Optimal harvesting-coefficient control of steady-state prey-predator diffusive Volterra-Lotka systems. Applied Mathematics and Optimization 1995,31(2):219-241. 10.1007/BF01182789
Gaines RE, Mawhin JL: Coincidence Degree, and Nonlinear Differential Equations, Lecture Notes in Mathematics. Volume 568. Springer, Berlin, Germany; 1977:i+262.
Chen Y: Multiple periodic solutions of delayed predator-prey systems with type IV functional responses. Nonlinear Analysis: Real World Applications 2004,5(1):45-53. 10.1016/S1468-1218(03)00014-2
Wang Q, Dai B, Chen Y: Multiple periodic solutions of an impulsive predator-prey model with Holling-type IV functional response. Mathematical and Computer Modelling 2009,49(9-10):1829-1836. 10.1016/j.mcm.2008.09.008
Hu D, Zhang Z: Four positive periodic solutions to a Lotka-Volterra cooperative system with harvesting terms. Nonlinear Analysis: Real World Applications 2010,11(2):1115-1121. 10.1016/j.nonrwa.2009.02.002
Zhao K, Ye Y: Four positive periodic solutions to a periodic Lotka-Volterra predatory-prey system with harvesting terms. Nonlinear Analysis: Real World Applications. In press
Acknowledgment
This work is supported by the National Natural Sciences Foundation of People's Republic of China under Grant no. 10971183.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Y., Zhao, K. Existence of  Positive Periodic Solutions to
Positive Periodic Solutions to  -Species Nonautonomous Food Chains with Harvesting Terms.
Adv Differ Equ 2010, 262461 (2010). https://doi.org/10.1155/2010/262461
-Species Nonautonomous Food Chains with Harvesting Terms.
Adv Differ Equ 2010, 262461 (2010). https://doi.org/10.1155/2010/262461
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/262461
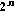 Positive Periodic Solutions
Positive Periodic Solutions , every solution
, every solution  of
of  is such that
is such that  ;
; for each
for each 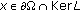 ;
;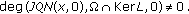
 and
and  are monotonically increasing and monotonically decreasing on the variable
are monotonically increasing and monotonically decreasing on the variable 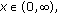 respectively.
respectively. and
and  are monotonically decreasing and monotonically increasing on the variable
are monotonically decreasing and monotonically increasing on the variable 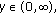 respectively.
respectively. and
and  are monotonically decreasing and monotonically increasing on the variable
are monotonically decreasing and monotonically increasing on the variable  respectively.
respectively. -species food-chain system with impulsive. Nonlinear Analysis: Real World Applications 2006,7(3):414-431. 10.1016/j.nonrwa.2005.03.009
-species food-chain system with impulsive. Nonlinear Analysis: Real World Applications 2006,7(3):414-431. 10.1016/j.nonrwa.2005.03.009 -species food-chain systems. Applied Mathematics and Computation 2005,167(1):324-344. 10.1016/j.amc.2004.06.082
-species food-chain systems. Applied Mathematics and Computation 2005,167(1):324-344. 10.1016/j.amc.2004.06.082