- Research Article
- Open access
- Published:
Existence of a Nonautonomous SIR Epidemic Model with Age Structure
Advances in Difference Equations volume 2010, Article number: 212858 (2010)
Abstract
A nonautonomous SIR epidemic model with age structure is studied. Using integro-differential equation and a fixed point theorem, we prove the existence and uniqueness of a positive solution to this model. We conclude our results and discuss some problems to this model in the future. We simulate our analyzed results.
1. Introduction
Age structure of a population affects the dynamics of disease transmission. Traditional transmission dynamics of certain diseases cannot be correctly described by the traditional epidemic models with no age-dependence. A simplemodel was first proposed by Lotka and Von Foerster [1, 2], where the birth and the death processes were independent of the total population size and so the limitation of the resources was not taken into account. To overcome this deficiency, Gurtin and MacCamy [3], in their pioneering work considered a nonlinear age-dependent model, where birth and death rates were function of the total population. Various age-structured epidemic models have been investigated by many authors, and a number of papers have been published on finding the threshold conditions for the disease to become endemic, describing the stability of steady-state solutions, and analyzing the global behavior of these age-structured epidemic models (see [4–7]). We may find that the epidemic models that most authors discussed mainly include S-I-R that is, the total population of a country or a district was subdivided into two or three compartments containing susceptibles, infectives, or immunes; it was assumed that there is no latent class, so a person who catches the disease becomes infectious instantaneously. The basic SIR age-structured epidemic model is like the following equations:

The non-autonomous phenomenon is so prevalent and all pervasive in the real life that modelling biological proceeding under non-autonomous environment should be more realistic than autonomous situation. The non-autonomous phenomenon is so prevalent in the real life that many epidemiological problems can be modeled by non-autonomous systems of nonlinear differential equations [8–11], which should be more realistic than autonomous differential equations. In one case, the incidence of many infectious diseases fluctuates over time and often exhibits periodic behavior. The basic SIR model is formulated by

These works were mainly concerned with finding threshold conditions for the disease to become endemic and describing the stability of steady-state solutions, often under the assumption that the population has reached its steady state and the diseases do not affect the death rate of the population.
However, all of the models which are not mixed age structure and non-autonomous are only concluding age structure or non-autonomous. Birth rate or input function is dependent on age or dependent on time  in these models cited therein. In fact, birth rate or input function is dependent not only on age
in these models cited therein. In fact, birth rate or input function is dependent not only on age  and time
and time  but also on the total population
but also on the total population  . We know the resource is limited. As recognized by authors, there was only one paper [3, 12] related them. In [3, 12], their model are two dimensions about epidemic dynamics. The population is increasing year after year. The birth rate is a decrease function until the population attend certain level such as Logistic growth rate. At the same time, the death rate should be dependent on the total population
. We know the resource is limited. As recognized by authors, there was only one paper [3, 12] related them. In [3, 12], their model are two dimensions about epidemic dynamics. The population is increasing year after year. The birth rate is a decrease function until the population attend certain level such as Logistic growth rate. At the same time, the death rate should be dependent on the total population  . We can consider now more realistic and complex models in which the epidemic acts in a different way on infected, susceptible and recovered (immune). We consider a well-known expression for the force of infection which is justified in the literature. We choose as
. We can consider now more realistic and complex models in which the epidemic acts in a different way on infected, susceptible and recovered (immune). We consider a well-known expression for the force of infection which is justified in the literature. We choose as  the natural space for the solution because the total population is finite.
the natural space for the solution because the total population is finite.
This paper is organized as follows: Section 2 introduces a non-autonomous SIR model with age structure. In Section 3, existence and uniqueness of a solution for an epidemic model with different mortality rates on any finite time-interval is obtained. In Section 4, we conclude our results and discuss the defect of our model.
2. The Model Formulation
This section describes the basic model we are going to analyze in this paper. The population is divided into three subclasses: susceptible, infected, and recovered. Where  denote the associated density functions with these respective epidemiological age-structured classes. Let
denote the associated density functions with these respective epidemiological age-structured classes. Let  ,
,  be the age-specific mortality of the susceptible, the infective and the recovered individuals at time
be the age-specific mortality of the susceptible, the infective and the recovered individuals at time  , respectively. We assume that the disease affects the death rate, so we have
, respectively. We assume that the disease affects the death rate, so we have  , and
, and  . We assume that all new born are susceptible whose birth process is described by
. We assume that all new born are susceptible whose birth process is described by

where  is the birth rate. We also suppose that the initial age distributions are given by
is the birth rate. We also suppose that the initial age distributions are given by  , and
, and  . And the age-specific recovery rate,
. And the age-specific recovery rate,  , is independent of the time. Then the joint dynamics of the age-structured epidemiological model for the transmission of SIR can be written as
, is independent of the time. Then the joint dynamics of the age-structured epidemiological model for the transmission of SIR can be written as

We supposes  and
and  belong to
belong to  . So,
. So,  and
and  , as
, as  . It is logical to satisfy the biological meaning. The horizontal transmission of the disease occurs according to the following law:
. It is logical to satisfy the biological meaning. The horizontal transmission of the disease occurs according to the following law:

where  is the rate at which an infective individual of age
is the rate at which an infective individual of age  comes into a disease transmitting contact with a susceptible individual of age
comes into a disease transmitting contact with a susceptible individual of age  . Summing the equations of (2.2), we obtain the following problem for the population density
. Summing the equations of (2.2), we obtain the following problem for the population density  .
.

In this paper, we prove the existence and uniqueness of a nonnegative solution of the model (2.2) on any finite time-interval. Our results are based on a process of the age-dependent problem for the susceptible the infected and the removed, and then a fixed point method. To study existence and uniqueness of a solution for an epidemic model with different mortality rates, we need the following hypotheses. Given  , we denote
, we denote  and we suppose that
and we suppose that
(H1) for  ,
,  is a nonnegative measurable function such that the mapping
is a nonnegative measurable function such that the mapping  belongs to
belongs to  for almost all
for almost all  . Moreover, there exists a constant
. Moreover, there exists a constant  such that for all
such that for all  ,
,

With the notation  ,
,  , there exists another constant
, there exists another constant  ,
,  such that
such that

(H2)  is a nonnegative measurable function which has compact support on the variable
is a nonnegative measurable function which has compact support on the variable  and such that for all
and such that for all  ,
,

where  is another constant which depends only on
is another constant which depends only on  . Moreover, there exists a constant
. Moreover, there exists a constant  such that for all
such that for all 

(H3)  has a compact support.
has a compact support.
(H4)  has compact support and is a nonnegative function. We set
has compact support and is a nonnegative function. We set .
.
(H5)  has a compact support and is a nonnegative function. We have
has a compact support and is a nonnegative function. We have .
.
To simplify the calculation of estimates, we perform the change

We obtain that the following system is analogous to (2.2).

where

For biological reasons, we are interested in nonnegative solutions, so we consider that

And we will look for solutions to (2.10) belonging to the following space:

endowed with the norm

where  is a positive constant which will be chosen later and
is a positive constant which will be chosen later and  denotes the usual norm in
denotes the usual norm in  that is,
that is, 
Namely, by a solution to (2.10), we mean a function

such that

In order to prove the existence of solution of (2.10), adding  in both sides of (2.16) in technical style, we have
in both sides of (2.16) in technical style, we have

where  ,
,  , and
, and  denote the directional derivatives of
denote the directional derivatives of  and
and  , respectively, that is,
, respectively, that is,

Generally,  will not be differentiable everywhere; of course,when this occurs,
will not be differentiable everywhere; of course,when this occurs,  ,
,  and
and  .
.
3. Existence of a Solution to the System
If we assume that  is smooth along the characteristics
is smooth along the characteristics  (except perhaps for a zero-measure set of
(except perhaps for a zero-measure set of  ), considering
), considering

where  , and integrating equalities of (2.16) along the line, we obtain the following ODS
, and integrating equalities of (2.16) along the line, we obtain the following ODS

Integrating (2.7) along  , we also get
, we also get  for technical need
for technical need

Integrating the second equation of (2.16) along  , we have
, we have

Integrating the third equation of (2.16) along  , we obtain
, we obtain

where

We can easily see that solving (2.16) is equivalent to finding a solution to (3.2), (3.4) and (3.5) or (3.3), (3.4), and (3.5) (see [3]). So, in the sequel, we restrict our attention to these integral equations.
Let us consider  with
with  , and
, and  fixed. Consider the set
fixed. Consider the set

The following result provides some useful estimates.
Lemma 3.1.
Suppose ( )–(
)–( ), and let
), and let  ,
, ,
,  , and
, and  . Then for
. Then for  ,
,
-
(i)
 (3.8)
(3.8) -
(ii)
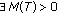 such that
such that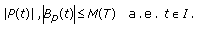 (3.9)
(3.9) -
(iii)
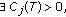 such that
such that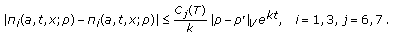 (3.10)
(3.10) -
(iv)
 such that
such that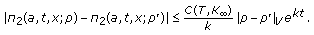 (3.11)
(3.11)
Proof.
Firstly, note that (3.8) and (3.9) are immediate. On the other hand,

We set  , and then
, and then

Lemma 3.2.
Suppose ( )–(
)–( ), if
), if  satisfies (3.2), (3.4), and (3.5), or (3.3), (3.4), and (3.5), then there exists a constant
satisfies (3.2), (3.4), and (3.5), or (3.3), (3.4), and (3.5), then there exists a constant  , depending only on
, depending only on  and
and  , such that
, such that  with
with  defined in (3.7).
defined in (3.7).
Proof.
Suppose that  satisfies the above assumptions. Considering (3.2), (3.4) and (3.5), or (3.3), (3.4), and (3.5), thanks to (3.7) and an obvious change of variables in the integrals, we have for all
satisfies the above assumptions. Considering (3.2), (3.4) and (3.5), or (3.3), (3.4), and (3.5), thanks to (3.7) and an obvious change of variables in the integrals, we have for all  ,
,

We use the Gronwall's inequality, and then

where  and
and  ,
,  .
.
Let us consider the map  , where
, where  is defined by
is defined by

and also  can be equal to
can be equal to



where  .
.
Lemma 3.3.
With the assumptions of Lemma 3.2, we have  .
.
Proof.
In this proof we denote, for abbreviation,

If  , then
, then  . Then
. Then  ,
,  ,
,  , by (2.5) and (2.7). Hence,
, by (2.5) and (2.7). Hence,  is clearly measurable in
is clearly measurable in  and essentially bounded on
and essentially bounded on  .
.
By (3.18),  , a.e.
, a.e.  . So, we only need to show that
. So, we only need to show that  ,
,  , a.e.
, a.e.  ,
,  , and
, and  , a.e.
, a.e.  . We assume that
. We assume that  (the discussion for
(the discussion for  is similar). Using (3.11) and (3.19) and substituting
is similar). Using (3.11) and (3.19) and substituting  and
and  into
into  we get
we get

Now, we proceed to estimate these quantities to see that  . By the mean value theorem, there exists
. By the mean value theorem, there exists  , such that
, such that

where

By the mean value theorem, there exists  , such that
, such that

and by the mean value theorem, there exists  , such that
, such that

We substitute  , and
, and  into the formula of
into the formula of  . Thus,
. Thus,

By the formula of  , we have
, we have  . Using (3.17) and (3.18) and substituting
. Using (3.17) and (3.18) and substituting  and
and  into
into  we get
we get

By the mean value theorem, there exists  , such that
, such that

By the mean value theorem, we have the following:

Thus,

So that  ,
,  , a.e.
, a.e.  , and we can conclude that for each
, and we can conclude that for each  ,
,  .
.
Theorem 3.4.
Suppose ( )–(
)–( ), for each
), for each  and for each
and for each  , with
, with  , there exists a unique
, there exists a unique  satisfying (3.2), (3.4), and (3.5), or (3.3), (3.4), and (3.5). And so,
satisfying (3.2), (3.4), and (3.5), or (3.3), (3.4), and (3.5). And so,  is the unique solution to problem (2.10).
is the unique solution to problem (2.10).
Proof.
In order to prove the theorem, it remains to be shown that  (defined by (3.11) and (3.18)) has a unique point fixed in
(defined by (3.11) and (3.18)) has a unique point fixed in  .
.
Let  be defined by (3.7); then for
be defined by (3.7); then for  being large enough
being large enough  maps
maps  into
into  . Indeed, by estimate of
. Indeed, by estimate of  , we get, for almost all
, we get, for almost all 

And from Gronwall's inequality, it follows that

for  depending on
depending on  ,
,  ,
,  and
and  . Hence, we have proved that
. Hence, we have proved that  maps
maps  into
into  .
.
Let us assume that  is fixed such that
is fixed such that  remains in
remains in  for
for  in
in  . Clearly,
. Clearly,  is closed in
is closed in  and to prove that
and to prove that  has a unique fixed point in
has a unique fixed point in  , it suffices to prove that
, it suffices to prove that  is a strict contraction, for instance for the norm defined in definition of
is a strict contraction, for instance for the norm defined in definition of  with
with  suitable. For convenience in the following we denote
suitable. For convenience in the following we denote  a certain (which may change) but which is independent of
a certain (which may change) but which is independent of  and
and  . For
. For  ,
,  , let us estimate
, let us estimate  .
.
First, for almost all  ,
,

Now, substituting the expression of  into
into  , we get
, we get

where  and
and  . Hence
. Hence

Estimate of . By (3.10), we have
. By (3.10), we have

Let us now estimate  . By (3.9) and (3.10), we get
. By (3.9) and (3.10), we get

Let us estimate  . Thanks to (2.7), (2.8), and (3.8), we have
. Thanks to (2.7), (2.8), and (3.8), we have

Second, let us estimate  . Substituting the expression for
. Substituting the expression for  into
into  and applying (3.11), we obtain
and applying (3.11), we obtain

Estimate of . By (2.6) and (3.8),
. By (2.6) and (3.8),  ,
,  , then
, then

Since  , we have
, we have  , and then
, and then

Finally, let us estimate of  .
.

Therefore, joining all above estimates, we see that for almost all  , there exist
, there exist  and
and  depending only on
depending only on  ,
,  ,
,  ,
,  ,
,  , and
, and  , such that
, such that

Dividing both sides of this inequality by  , we obtain
, we obtain

And thus for  great enough
great enough  is a strict contraction with a unique fixed point in
is a strict contraction with a unique fixed point in  , and so in
, and so in  . This concludes the proof.
. This concludes the proof.
4. Discussion
In this paper, existence of positive period solution of a non-autonomous SIR epidemic model with age structure is studied. We obtained existence and uniqueness of this model using integral differential equation and a fixed theorem. The model is different from the classical age structure epidemic model and non-autonomous epidemic model. The initial condition is nonlocal and dependent on total population. In addition, incidence law is not Lipschitzianity. The classical methods are not valid. We construct a new norm and prove the existence of our model under definition of the new norm. We can illustrate this through two simulates examples. We set

System (2.2) with above coefficients has a unique positive periodic solution. We can see it from Figure 1.
In the future, there are some problems that will be solved. The existence of steady state and stability of the steady state are still discussed. If birth rate is impulsive, what results will occur. The simulation of the age structure still to be resolved. Furthermore, what effect will occurs, if we introduce the delay in our model.
References
Lotka AJ: Elements of Mathematical Biology. Dover, New York, NY, USA; 1956.
Von Foerster H: Some remarks on changing populations. In The Kinetics of Cellular Proliferation. Grune & Stratton, New York, NY, USA; 1959:382-407.
Gurtin ME, MacCamy RC: Non-linear age-dependent population dynamics. Archive for Rational Mechanics and Analysis 1974, 54: 281-300. 10.1007/BF00250793
Busenberg SN, Iannelli M, Thieme HR: Global behavior of an age-structured epidemic model. SIAM Journal on Mathematical Analysis 1991,22(4):1065-1080. 10.1137/0522069
Iannelli M, Milner FA, Pugliese A: Analytical and numerical results for the age-structured S-I-S epidemic model with mixed inter-intracohort transmission. SIAM Journal on Mathematical Analysis 1992,23(3):662-688. 10.1137/0523034
El-Doma M: Analysis for an SIR age-structured epidemic model with vertical transmission and vaccination. International Journal of Ecology and Development 2005, 3: 1-38.
Webb GF: Theory of Nonlinear Age-Dependent Population Dynamics, Monographs and Textbooks in Pure and Applied Mathematics. Volume 89. Marcel Dekker, New York, NY, USA; 1985:vi+294.
Thieme HR: Uniform weak implies uniform strong persistence for non-autonomous semiflows. Proceedings of the American Mathematical Society 1999,127(8):2395-2403. 10.1090/S0002-9939-99-05034-0
Wang W, Zhao X-Q: Threshold dynamics for compartmental epidemic models in periodic environments. Journal of Dynamics and Differential Equations 2008,20(3):699-717. 10.1007/s10884-008-9111-8
Zhang T, Teng Z: Permanence and extinction for a nonautonomous SIRS epidemic model with time delay. Applied Mathematical Modelling 2009,33(2):1058-1071. 10.1016/j.apm.2007.12.020
Teng Z, Liu Y, Zhang L: Persistence and extinction of disease in non-autonomous SIRS epidemic models with disease-induced mortality. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2599-2614. 10.1016/j.na.2007.08.036
Delgado M, Molina-Becerra M, Suárez A: Analysis of an age-structured predator-prey model with disease in the prey. Nonlinear Analysis: Real World Applications 2006,7(4):853-871. 10.1016/j.nonrwa.2005.03.031
Acknowledgments
This work is Supported by the National Sciences Foundation of China (10971178), the Sciences Foundation of Shanxi (20090110053), and the Sciences Exploited Foundation of Shanxi (20081045).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, J., Wang, X. Existence of a Nonautonomous SIR Epidemic Model with Age Structure. Adv Differ Equ 2010, 212858 (2010). https://doi.org/10.1155/2010/212858
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/212858

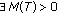 such that
such that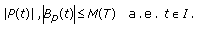
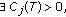 such that
such that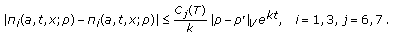
 such that
such that