- Research Article
- Open access
- Published:
On an Exponential-Type Fuzzy Difference Equation
Advances in Difference Equations volume 2010, Article number: 196920 (2010)
Abstract
Our goal is to investigate the existence of the positive solutions, the existence of a nonnegative equilibrium, and the convergence of a positive solution to a nonnegative equilibrium of the fuzzy difference equation  ,
,  ,
,  , where
, where  and the initial values
and the initial values  belong in a class of fuzzy numbers.
belong in a class of fuzzy numbers.
1. Introduction
Fuzzy difference equations are approached by many authors, from a different view.
In [1], the authors developed the stability results for the fuzzy difference equation

in terms of the stability of the trivial solution of the ordinary difference equation

where  is continuous in
is continuous in  for each
for each  , and
, and  for each
for each  , where
, where  such that
such that  satisfies the following:
satisfies the following:
-
(i)
 is normal;
is normal; -
(ii)
 is fuzzy convex;
is fuzzy convex; -
(iii)
 is upper semicontinuous;
is upper semicontinuous; -
(iv)
 is compact, and
is compact, and  is a continuous and nondecreasing function in
is a continuous and nondecreasing function in  for each
for each  .
.
In [2], the authors studied the second-order, linear, constant coefficient fuzzy difference equation of the form

for  , where
, where  is the unknown function of
is the unknown function of  and
and  are real constants with
are real constants with  .
.  is a known function of
is a known function of  and
and  parameters
parameters  , which is continuous in
, which is continuous in  . The initial conditions are fuzzy sets.
. The initial conditions are fuzzy sets.
In [3] the authors considered the associated fuzzy system

of the deterministic system

where  is the Zadeh's extensions of a continuous function
is the Zadeh's extensions of a continuous function  . Equations (1.4) and (1.5) have the same real constants coefficient and real equilibriums.
. Equations (1.4) and (1.5) have the same real constants coefficient and real equilibriums.
In this paper, we consider the fuzzy difference equation

where  and the initial values are in a class of fuzzy numbers (see Preliminaries). This equation is motivated by the corresponding ordinary difference equation which is posed in [4]. Moreover, (1.6) is a special case of an epidemic model (see [5–8]) and was studied in [9] by Zhang and Shi and in [10] by Stević.
and the initial values are in a class of fuzzy numbers (see Preliminaries). This equation is motivated by the corresponding ordinary difference equation which is posed in [4]. Moreover, (1.6) is a special case of an epidemic model (see [5–8]) and was studied in [9] by Zhang and Shi and in [10] by Stević.
In [11] we have, already, investigated the behavior of the solutions of a related system of two parametric ordinary difference equations, of the form

where  are positive real numbers and the initial values
are positive real numbers and the initial values  ,
,  ,
,  , are positive real numbers, which satisfy some additional conditions.
, are positive real numbers, which satisfy some additional conditions.
We note that, the behavior of the fuzzy difference equation is not always the same with the corresponding ordinary difference equation. For instance, in paper [12] the fuzzy difference equation

where  are positive integers,
are positive integers,  , and the initial values
, and the initial values  ,
,  ,
,  are in a class of fuzzy numbers, under some conditions has unbounded solutions, something that does not happen in the case of the corresponding ordinary difference equation (1.8), where
are in a class of fuzzy numbers, under some conditions has unbounded solutions, something that does not happen in the case of the corresponding ordinary difference equation (1.8), where  are positive integers and
are positive integers and  , and the initial values
, and the initial values  ,
,  ,
,  are positive real numbers.
are positive real numbers.
Finally we note that in recent years there has been a considerable interest in the study of the existence of some specific classes of solutions of difference equations such as nontrivial, nonoscillatory, monotone, positive. Various methods have been developed by the experts. For partial review of the theory of difference equations and their applications see, for example, [4, 10, 13–27] and the references therein.
2. Preliminaries
For a set  , we denote by
, we denote by  the closure of
the closure of  .
.
We denote by  the set of functions
the set of functions  such that,
such that,

where  satisfies the following conditions:
satisfies the following conditions:
-
(i)
 is normal, that is, there exists an
is normal, that is, there exists an  such that
such that 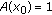 ;
; -
(ii)
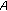 is fuzzy convex, that is for
is fuzzy convex, that is for 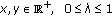 ;
;  (2.2)
(2.2) -
(iii)
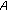 is upper semicontinuous
is upper semicontinuous -
(iv)
The support of
 ,
,  is compact.
is compact.
Obviously, set  is a class of fuzzy numbers. In this paper, all the fuzzy numbers we use are elements of
is a class of fuzzy numbers. In this paper, all the fuzzy numbers we use are elements of  . From above (i)–(iv) and Theorems
. From above (i)–(iv) and Theorems  and
and  of [28] the
of [28] the  -cuts of the fuzzy number
-cuts of the fuzzy number  ,
,

are closed intervals. Obviously,  .
.
We say that a fuzzy number  is positive if
is positive if  .
.
To prove our main results, we need the following theorem (see [29]).
Theorem 2.1 (see [29]).
Let  , such that
, such that  ,
,  . Then
. Then  can be regarded as functions on
can be regarded as functions on  which satisfy
which satisfy
-
(i)
 is nondecreasing and left continuous;
is nondecreasing and left continuous; -
(ii)
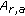 is nonincreasing and left continuous;
is nonincreasing and left continuous; -
(iii)
 .
.
Conversely, for any functions  defined in
defined in  which satisfy (i)–(iii) in above and
which satisfy (i)–(iii) in above and  is compact, there exists a unique
is compact, there exists a unique  such that
such that  ,
,  .
.
We need the following arithmetic operations on closed intervals:
-
(i)
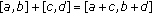 ,
, 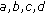 positive real numbers,
positive real numbers, -
(ii)
 ,
,  positive real numbers,
positive real numbers, -
(iii)
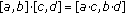 ,
, 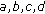 positive real numbers.
positive real numbers.
In this paper, we use the following arithmetic operations on fuzzy numbers based on closed intervals arithmetic (see [30]). Let  be positive fuzzy numbers which belong to
be positive fuzzy numbers which belong to  with
with

-
(i)
 is a positive fuzzy number which belongs to
is a positive fuzzy number which belongs to 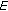 , with
, with  (2.5)
(2.5) -
(ii)
 is a positive fuzzy number which belongs to
is a positive fuzzy number which belongs to  , with
, with 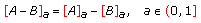 (2.6)
(2.6)if
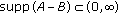 ;
; -
(iii)
 is a positive fuzzy number which belongs to
is a positive fuzzy number which belongs to  , with
, with 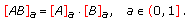 (2.7)
(2.7)
We note that the subtraction "−" we use, is different than Hukuhara difference (see [31, 32]).
Using Extension Principle (see [28, 30, 33]) for a positive fuzzy number  such that (2.4) holds, we have
such that (2.4) holds, we have

Let  be positive fuzzy numbers which belong to
be positive fuzzy numbers which belong to  such that (2.4) holds. We consider the following metric (see [29, 32]):
such that (2.4) holds. We consider the following metric (see [29, 32]):

where  is taken for all
is taken for all  .
.
We say  is a positive solution of (1.6) if
is a positive solution of (1.6) if  is a sequence of positive fuzzy numbers which satisfies (1.6).
is a sequence of positive fuzzy numbers which satisfies (1.6).
We say that a positive fuzzy number  is a positive equilibrium for (1.6) if
is a positive equilibrium for (1.6) if

Let  be a sequence of positive fuzzy numbers and
be a sequence of positive fuzzy numbers and  is a positive fuzzy number. Suppose that
is a positive fuzzy number. Suppose that

are satisfied. We say that  nearly converges to
nearly converges to  with respect to
with respect to  as
as  if for every
if for every  there exists a measurable set
there exists a measurable set  ,
,  of measure less than
of measure less than  such that
such that

where

If  , we say that
, we say that  converges to
converges to  with respect to
with respect to  as
as  .
.
Let  be the set of positive fuzzy numbers. From Theorem 2.1 we have that
be the set of positive fuzzy numbers. From Theorem 2.1 we have that  (resp.,
(resp.,  ) are increasing (resp., decreasing) functions on
) are increasing (resp., decreasing) functions on  . Therefore, using the condition (iv) of the definition of the fuzzy numbers there exist the Lebesque integrals
. Therefore, using the condition (iv) of the definition of the fuzzy numbers there exist the Lebesque integrals

where . We define the function
. We define the function 
 such that
such that

If  we have that there exists a measurable set
we have that there exists a measurable set  of measure zero such that
of measure zero such that

We consider however, two fuzzy numbers  to be equivalent if there exists a measurable set
to be equivalent if there exists a measurable set  of measure zero such that (2.16) hold and if we do not distinguish between equivalent of fuzzy numbers then
of measure zero such that (2.16) hold and if we do not distinguish between equivalent of fuzzy numbers then  becomes a metric space with metric
becomes a metric space with metric  .
.
We say that a sequence of positive fuzzy numbers  converges to a positive fuzzy number
converges to a positive fuzzy number  with respect to
with respect to  as
as  if
if

3. Study of the Fuzzy Difference Equation (1.6)
In order to prove our main results, we need the following Propositions A, B, C, which can be found in [11]. For readers convenience, we cite them below without their proofs.
Proposition A (see [11]).
Consider system (1.7) where the constants  are positive real numbers. Let
are positive real numbers. Let  be a solution of (1.7) with initial values
be a solution of (1.7) with initial values  ,
,  ,
,  ,
,  . Then the following statements are true.
. Then the following statements are true.
-
(i)
Suppose that
 (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3)hold. Then
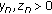 ,
, 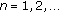 .
. -
(ii)
Suppose that
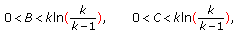 (3.4)
(3.4)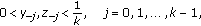 (3.5)
(3.5)hold. Then
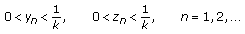 (3.6)
(3.6)
Proposition B (see [11]).
Consider the system of algebraic equations

Then the following statements are true.
-
(i)
If (3.2) holds, the system (3.7) has a unique nonnegative solution
 .
. -
(ii)
Suppose that
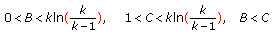 (3.8)
(3.8)
hold; then there are only two nonnegative equilibriums  of system (3.7), such that
of system (3.7), such that  , which are
, which are  ,
,  ,
,  .
.
Proposition C (see [11]).
Consider system (1.7). Let  be a solution of (1.7). Then the following statements are true.
be a solution of (1.7). Then the following statements are true.
-
(i)
If (3.2) and either (3.1) and (3.3) or (3.5) are satisfied, then for the solution
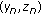 of system (1.7) we have that
of system (1.7) we have that 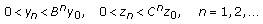 (3.9)
(3.9)holds and obviously
 tends to the unique zero equilibrium
tends to the unique zero equilibrium  of (1.7) as
of (1.7) as 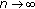 .
. -
(ii)
Suppose that (3.5), the first relation of (3.2) and the second relation of (3.8) are satisfied. Then
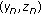 tends to the nonnegative equilibrium
tends to the nonnegative equilibrium  ,
, 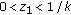 of (1.7) as
of (1.7) as 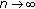 .
.
First we study the existence and the uniqueness of the positive solutions of the fuzzy difference equation (1.6).
Proposition 3.1.
Consider the fuzzy difference equation (1.6), where  is a positive fuzzy number such that
is a positive fuzzy number such that

Let  be fuzzy numbers and
be fuzzy numbers and  ,
,  ,
,  positive real numbers such that
positive real numbers such that

Then the following statements are true.
-
(i)
Suppose that
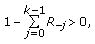 (3.12)
(3.12) (3.13)
(3.13) (3.14)
(3.14)hold. Then there exists a unique positive solution
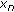 of the fuzzy difference equation (1.6) with initial values
of the fuzzy difference equation (1.6) with initial values 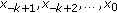 .
. -
(ii)
Suppose that
 (3.15)
(3.15)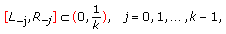 (3.16)
(3.16)hold. Then there exists a unique positive solution
 of the fuzzy difference equation (1.6) with initial values
of the fuzzy difference equation (1.6) with initial values 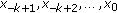 .
.
Proof.
We consider the family of systems of parametric ordinary difference equations for  and
and  ,
,

-
(i)
From (3.11) and (3.14), we can consider that
 (3.18)
(3.18)
Using relations (3.10)–(3.13), (3.18), and Proposition A, we get that the system of ordinary difference equations

with initial values  ,
,  , has a positive solution
, has a positive solution  and so
and so

In addition, from (3.10)–(3.14) and Proposition A, we have that (3.17) has a positive solution  ,
,  , with initial values
, with initial values  ,
,  . We prove that
. We prove that  ,
,  determines a sequence of positive fuzzy numbers.
determines a sequence of positive fuzzy numbers.
Since  ,
,  and
and  are positive fuzzy numbers, from Theorem 2.1 we have that
are positive fuzzy numbers, from Theorem 2.1 we have that  ,
,  , and
, and  ,
,  , are left continues and so from (3.17), we get that
, are left continues and so from (3.17), we get that  are left continuous as well.
are left continuous as well.
In addition, for any  ,
, , we have
, we have

and so from (3.10)–(3.13), and (3.17)

Moreover, from (3.10)–(3.13), (3.17), and (3.19), we get

Therefore, from Theorem 2.1 relations (3.22), (3.23), and since  are left continuous, we have that
are left continuous, we have that  determine a positive fuzzy number
determine a positive fuzzy number  such that
such that

Since  ,
,  are left continuous from (3.17) and working inductively, we get that
are left continuous from (3.17) and working inductively, we get that  ,
,  ,
,  are also left continuous. In addition, using (3.10), (3.11), (3.13), (3.17), (3.20), (3.21), (3.22), and working inductively, we get for any
are also left continuous. In addition, using (3.10), (3.11), (3.13), (3.17), (3.20), (3.21), (3.22), and working inductively, we get for any  ,
, and
and 

Finally, using (3.10), (3.11), (3.13), (3.17), (3.19), (3.20), (3.23), and working inductively, we get for 

where  is the solution of (3.19).
is the solution of (3.19).
Therefore, since  ,
,  ,
,  are left continuous and (3.22), (3.23), (3.25), (3.26) are satisfied, from Theorem 2.1, we get that the positive solution
are left continuous and (3.22), (3.23), (3.25), (3.26) are satisfied, from Theorem 2.1, we get that the positive solution  ,
,  ,
, , of (3.17), with initial values
, of (3.17), with initial values  ,
,  ,
,  ,
, satisfying (3.11), (3.12), (3.14), determines a sequence of positive fuzzy numbers
satisfying (3.11), (3.12), (3.14), determines a sequence of positive fuzzy numbers  , such that
, such that

We claim that  is a solution of (1.6) with initial values
is a solution of (1.6) with initial values  ,
,  , such that (3.11), (3.12), and (3.14) hold. From (3.17) and (3.27) we have for all
, such that (3.11), (3.12), and (3.14) hold. From (3.17) and (3.27) we have for all 

In addition, from (3.10), (3.23), and (3.26), we get

and so from (3.17), (3.23), and (3.26)

Therefore, using (3.28) and arithmetic multiplication on closed intervals

Using arithmetic operations on positive fuzzy numbers and (2.8) we have

and thus, our claim is true.
Finally, suppose that there exists another solution  of the fuzzy difference equation (1.6) with initial values
of the fuzzy difference equation (1.6) with initial values  ,
,  , such that (3.10)–(3.14) hold. Then using the uniqueness of the solutions of the system (3.17) and arithmetic operations on positive fuzzy numbers and (2.8), we can easily prove that
, such that (3.10)–(3.14) hold. Then using the uniqueness of the solutions of the system (3.17) and arithmetic operations on positive fuzzy numbers and (2.8), we can easily prove that

and so we have that  is the unique positive solution of the fuzzy difference equation (1.6) with initial values
is the unique positive solution of the fuzzy difference equation (1.6) with initial values  ,
,  , such that (3.11), (3.12), and (3.14) hold. This completes the proof of statement (i).
, such that (3.11), (3.12), and (3.14) hold. This completes the proof of statement (i).
-
(ii)
From (3.10), (3.15), (3.16), and Proposition A, we get that system (3.19) with initial values
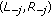 ,
,  has a positive solution
has a positive solution  such that (3.20) and
such that (3.20) and  (3.34)
(3.34)
hold.
From (3.10), (3.11), (3.15), (3.16), and Proposition A, we have that (3.17) has a positive solution  ,
,  , with initial values
, with initial values  ,
,  , such that
, such that

We prove that  ,
,  determines a sequence of positive fuzzy numbers.
determines a sequence of positive fuzzy numbers.
From (3.10), (3.11), (3.15)–(3.17), (3.19), and (3.20), we get that (3.23) holds. Moreover, arguing as in statement (i), we can easily prove that  determine a positive fuzzy number
determine a positive fuzzy number  such that (3.24) holds.
such that (3.24) holds.
As in statement (i), using (3.10), (3.11), (3.15)–(3.17), (3.24), Theorem 2.1 and working inductively, we get that the positive solution  ,
,  ,
,  , of (3.17), determines a sequence of positive fuzzy numbers
, of (3.17), determines a sequence of positive fuzzy numbers  , such that (3.27) holds.
, such that (3.27) holds.
Finally, arguing as in statement (i) we have that  is the unique positive solution of the fuzzy difference equation (1.6) with initial values
is the unique positive solution of the fuzzy difference equation (1.6) with initial values  ,
,  , such that (3.10), (3.11), (3.15) and (3.16) hold. This completes the proof of the proposition.
, such that (3.10), (3.11), (3.15) and (3.16) hold. This completes the proof of the proposition.
In the next proposition we study the existence of nonnegative equilibriums of the fuzzy difference equation (1.6).
Proposition 3.2.
Consider the fuzzy difference equation (1.6) where  is a positive fuzzy number such that (3.10) holds and the initial values
is a positive fuzzy number such that (3.10) holds and the initial values  ,
,  are positive fuzzy numbers. Then the following statements are true.
are positive fuzzy numbers. Then the following statements are true.
-
(i)
If
 (3.36)
(3.36)then zero is the unique nonnegative equilibrium of the fuzzy difference equation (1.6).
-
(ii)
If
 (3.37)
(3.37)then zero and
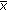 where
where (3.38)
(3.38)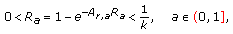 (3.39)
(3.39)are the only nonnegative equilibriums of the fuzzy difference equation (1.6), such that (2.11) and
 hold.
hold.
Proof.
We consider the fuzzy equation

where  is a positive fuzzy number such that (3.10) holds. Suppose that
is a positive fuzzy number such that (3.10) holds. Suppose that  , is a solution of (3.40) such that
, is a solution of (3.40) such that

Then using arithmetic operations on fuzzy numbers and (2.8), (3.10), we can easily prove that  satisfies the family of parametric algebraic systems
satisfies the family of parametric algebraic systems

-
(i)
If (3.36) holds then from (3.10), (3.41), (3.42), and statement (i) of Proposition B, we get that
 (3.43)
(3.43)This completes the proof of statement (i).
-
(ii)
If (3.37) and (3.41) hold then from (3.10) and statement (ii) of Proposition B, we get that system (3.42) has only two solutions, which are
 (3.44)
(3.44)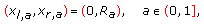 (3.45)
(3.45)where
 ,
, 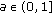 , is the unique function which satisfies (3.39).
, is the unique function which satisfies (3.39).
Using (3.41) and (3.44) we have that zero is a solution of the fuzzy equation (3.40).
To continue, we have to prove that  ,
,  , determines a fuzzy number, where
, determines a fuzzy number, where  , satisfies (3.39). From (3.39), we get
, satisfies (3.39). From (3.39), we get

We consider the function

then

We can easily prove that

is an increasing and positive function for  and so using (3.48), we get that
and so using (3.48), we get that  is an increasing function for
is an increasing function for  . Since
. Since  is a positive, decreasing function with respect to
is a positive, decreasing function with respect to  ,
,  , we get that
, we get that

and so from (3.46)

which means that

since  is an increasing function. From (3.52) it is obvious that
is an increasing function. From (3.52) it is obvious that  is a decreasing function with respect to
is a decreasing function with respect to  ,
,  .
.
In addition, since  is a continuous and increasing function, we have that
is a continuous and increasing function, we have that  is also a continuous and increasing function. Moreover,
is also a continuous and increasing function. Moreover,  is a left continuous function with respect to
is a left continuous function with respect to  ,
,  .
.
Therefore,

is a left continues function with respect to  ,
,  .
.
Finally, from (3.39) we have that

From Theorem 2.1, (3.39), (3.52), (3.54), and since  is a left continuous function with respect to
is a left continuous function with respect to  ,
,  , we have that
, we have that  ,
,  determines a fuzzy number
determines a fuzzy number  such that (3.38) holds. Therefore, from (3.45)
such that (3.38) holds. Therefore, from (3.45)  is a solution of the fuzzy equation (3.40). This completes the proof of the proposition.
is a solution of the fuzzy equation (3.40). This completes the proof of the proposition.
In the last proposition we study the asymptotic behavior of the positive solutions of the fuzzy difference equation (1.6).
Proposition 3.3.
Consider the fuzzy difference equation (1.6) where  is a positive fuzzy number such that (3.10) holds. Let
is a positive fuzzy number such that (3.10) holds. Let  ,
,  be the initial values such that (3.11) holds. Then the following statements are true.
be the initial values such that (3.11) holds. Then the following statements are true.
-
(i)
Suppose that
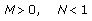 (3.55)
(3.55)and either (3.12) and (3.14) or (3.16) are satisfied. Then every positive solution of the fuzzy difference equation (1.6) tends to the zero equilibrium as
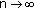 .
. -
(ii)
Suppose that
 (3.56)
(3.56)and (3.16) are satisfied. Then every positive solution of the fuzzy difference equation (1.6) nearly converges to the nonnegative equilibrium
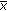 with respect to
with respect to  as
as  and converges to
and converges to 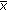 with respect to
with respect to  as
as 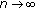 , where
, where  was defined by (3.38) and (3.39).
was defined by (3.38) and (3.39).
Proof.
(i) Since (3.55) and either (3.12) and (3.14) or (3.16) are satisfied, from Proposition 3.1 the fuzzy difference equation (1.6) has unique positive solution  , such that (3.27) holds.
, such that (3.27) holds.
In addition, (3.10) and (3.55) imply that (3.36) holds. So, from statement (i) of Proposition 3.2, zero is the unique nonnegative equilibrium of the fuzzy difference equation (1.6).
From the analogous relation of (3.9) of Proposition C and using (3.10), (3.11), we get

and since

where  and
and  is taken for all
is taken for all  , from (3.55) and (3.57), we get
, from (3.55) and (3.57), we get

This completes the proof of statement (i).
(ii) Since from (3.56), we have that (3.15) and (3.37) are fulfilled, we get from (3.16) and statement (ii) of Propositions 3.1 and 3.2 that the fuzzy difference equation (1.6) has unique positive solution  such that (3.27) holds, and a nonnegative equilibrium
such that (3.27) holds, and a nonnegative equilibrium  , such that (3.38) and (3.39) hold. Since
, such that (3.38) and (3.39) hold. Since  is a positive solution of system (3.17), from (3.11), (3.16), (3.56), and Proposition C we have that
is a positive solution of system (3.17), from (3.11), (3.16), (3.56), and Proposition C we have that

Using (3.60) and arguing as in Proposition  of [34], we can prove that the positive solution
of [34], we can prove that the positive solution  of (1.6) nearly converges to
of (1.6) nearly converges to  with respect to
with respect to  as
as  and converges to
and converges to  with respect to
with respect to  as
as  . Thus, the proof of the proposition is completed.
. Thus, the proof of the proposition is completed.
To illustrate our results we give some examples in which the conditions of our propositions hold.
Example 3.4.
Consider the fuzzy equation (1.6) for 

where  is a fuzzy number such that
is a fuzzy number such that

We take the initial values  such that
such that

From (3.62), we get

and so

Moreover from (3.63) we take

and so

Therefore the conditions (3.10)–(3.14) are satisfied. So from statement (i) of Proposition 3.1 the solution  of (3.61) with initial values
of (3.61) with initial values  is positive and unique. In addition it is obvious that (3.36) are satisfied. Then from the statement (i) of Proposition 3.2 we have that zero is the unique nonnegative equilibrium of (3.61). Finally from Proposition 3.3 the unique positive solution
is positive and unique. In addition it is obvious that (3.36) are satisfied. Then from the statement (i) of Proposition 3.2 we have that zero is the unique nonnegative equilibrium of (3.61). Finally from Proposition 3.3 the unique positive solution  of (3.61) with initial values
of (3.61) with initial values  tends to the zero equilibrium of (3.61) as
tends to the zero equilibrium of (3.61) as  .
.
Example 3.5.
Consider the fuzzy equation (3.61) where  is a fuzzy number such that
is a fuzzy number such that

We take the initial values  such that
such that

From (3.68), we get

and so

Moreover from (3.69) we take

and so

Therefore the conditions (3.15), (3.16) are satisfied. So from statement (ii) of Proposition 3.1 the solution  of (3.61) with initial values
of (3.61) with initial values  is positive and unique.
is positive and unique.
Example 3.6.
We consider equation (3.61) where the fuzzy number  is given as follows
is given as follows

Then from (3.74), we get

Then it is obvious that (3.37) are satisfied. Then from the statement (ii) of Proposition 3.2 we have that zero and  where
where  ,
,  ,
,  ,
,  are the only nonnegative equilibriums of the fuzzy difference equation (3.61), such that (2.11) and
are the only nonnegative equilibriums of the fuzzy difference equation (3.61), such that (2.11) and  hold.
hold.
Example 3.7.
We consider the fuzzy difference equation (3.61) where  is given by (3.62). Let
is given by (3.62). Let  ,
,  be the fuzzy numbers given by (3.69). Then since (3.15), (3.16), and (3.36) hold from Propositions 3.1, 3.2 and 3.3 the unique positive solution
be the fuzzy numbers given by (3.69). Then since (3.15), (3.16), and (3.36) hold from Propositions 3.1, 3.2 and 3.3 the unique positive solution  of (3.61) with initial values
of (3.61) with initial values  tends to the zero equilibrium of (3.61) as
tends to the zero equilibrium of (3.61) as  .
.
Example 3.8.
Consider the fuzzy difference equation (3.61) where the fuzzy number  is given by
is given by

Then from (3.76), we get

Then it is obvious that relations (3.37) are satisfied. So from the statement (ii) of Proposition 3.2 we have that zero and  where
where  ,
,  ,
,  ,
,  are the only nonnegative equilibriums of the fuzzy difference equation (3.61), such that (2.11) and
are the only nonnegative equilibriums of the fuzzy difference equation (3.61), such that (2.11) and  hold. Let
hold. Let  be the fuzzy numbers defined in (3.69). Then from the statement (ii) of Proposition 3.1 and statement (ii) of Proposition 3.3 we have that the unique positive solution
be the fuzzy numbers defined in (3.69). Then from the statement (ii) of Proposition 3.1 and statement (ii) of Proposition 3.3 we have that the unique positive solution  of (3.61) with initial values
of (3.61) with initial values  nearly converges to the nonnegative equilibrium
nearly converges to the nonnegative equilibrium  with respect to
with respect to  as
as  and converges to
and converges to  with respect to
with respect to  as
as  .
.
4. Conclusions
In this paper, we considered the fuzzy difference equation (1.6), where  and the initial values
and the initial values  are positive fuzzy numbers. The corresponding ordinary difference equation (1.6) is a special case of an epidemic model. The combine of difference equations and Fuzzy Logic is an extra motivation for studying this equation. A mathematical modelling of a real world phenomenon, very often, leads to a difference equation and on the other hand, Fuzzy Logic can handle uncertainness, imprecision or vagueness related to the experimental input-output data.
are positive fuzzy numbers. The corresponding ordinary difference equation (1.6) is a special case of an epidemic model. The combine of difference equations and Fuzzy Logic is an extra motivation for studying this equation. A mathematical modelling of a real world phenomenon, very often, leads to a difference equation and on the other hand, Fuzzy Logic can handle uncertainness, imprecision or vagueness related to the experimental input-output data.
The main results of this paper are the following. Firstly, under some conditions on  and initial values we found positive solutions and nonnegative equilibriums and then we studied the convergence of the positive solutions to the nonnegative equilibrium of the fuzzy difference equations (1.6). We note that, in order to study the fuzzy difference equation (1.6), we used the results concerning the behavior of the solutions of the related system of two parametric ordinary difference equations (1.7) (see [11]).
and initial values we found positive solutions and nonnegative equilibriums and then we studied the convergence of the positive solutions to the nonnegative equilibrium of the fuzzy difference equations (1.6). We note that, in order to study the fuzzy difference equation (1.6), we used the results concerning the behavior of the solutions of the related system of two parametric ordinary difference equations (1.7) (see [11]).
References
Lakshmikantham V, Vatsala AS: Basic theory of fuzzy difference equations. Journal of Difference Equations and Applications 2002,8(11):957-968. 10.1080/1023619021000048850
Buckley JJ, Feuring T, Hayashi Y: Fuzzy difference equations: the initial value problem. Journal of Advanced Computational Intelligence 2001,5(6):315-325.
Bassanezi RC, de Barros LC, Tonelli PA: Attractors and asymptotic stability for fuzzy dynamical systems. Fuzzy Sets and Systems 2000,113(3):473-483. 10.1016/S0165-0114(98)00142-0
Kocić VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and Its Applications. Volume 256. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+228.
Beddington JR, Free CA, Lawton JH: Dynamic complexity in predator prey models framed in difference equations. Nature 1975,255(5503):58-60. 10.1038/255058a0
Cooke KL, Calef DF, Level EV: Stability or chaos in discrete epidemic models. In Nonlinear Systems and Applications. Academic Press, New York, NY, USA; 1977:73-93.
Gu E-G: The nonlinear analysis on a discrete host-parasitoid model with pesticidal interference. Communications in Nonlinear Science and Numerical Simulation 2009,14(6):2720-2727. 10.1016/j.cnsns.2008.08.012
Kendall BE: Cycles, chaos, and noise in predator-prey dynamics. Chaos, Solitons and Fractals 2001,12(2):321-332. 10.1016/S0960-0779(00)00180-6
Zhang DC, Shi B: Oscillation and global asymptotic stability in a discrete epidemic model. Journal of Mathematical Analysis and Applications 2003,278(1):194-202. 10.1016/S0022-247X(02)00717-5
Stević S: On a discrete epidemic model. Discrete Dynamics in Nature and Society 2007, 2007:-10.
Stefanidou G, Papaschinopoulos G, Schinas CJ: On a system of two exponential type difference equations. Communications on Applied Nonlinear Analysis 2010,17(2):1-13.
Stefanidou G, Papaschinopoulos G: The periodic nature of the positive solutions of a nonlinear fuzzy max-difference equation. Information Sciences 2006,176(24):3694-3710. 10.1016/j.ins.2006.02.006
Berg L: On the asymptotics of nonlinear difference equations. Zeitschrift für Analysis und ihre Anwendungen 2002,21(4):1061-1074.
Berg L: Inclusion theorems for non-linear difference equations with applications. Journal of Difference Equations and Applications 2004,10(4):399-408. 10.1080/10236190310001625280
Berg L: On the asymptotics of the difference equation
 . Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041
. Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041Gutnik L, Stević S: On the behaviour of the solutions of a second-order difference equation. Discrete Dynamics in Nature and Society 2007, 2007:-14.
Iričanin B, Stević S: Eventually constant solutions of a rational difference equation. Applied Mathematics and Computation 2009,215(2):854-856. 10.1016/j.amc.2009.05.044
Kent CM: Convergence of solutions in a nonhyperbolic case. Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4651-4665. 10.1016/S0362-546X(01)00578-8
Stević S: On the recursive sequence
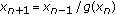 . Taiwanese Journal of Mathematics 2002,6(3):405-414.
. Taiwanese Journal of Mathematics 2002,6(3):405-414.Stević S: Global stability and asymptotics of some classes of rational difference equations. Journal of Mathematical Analysis and Applications 2006,316(1):60-68. 10.1016/j.jmaa.2005.04.077
Stević S: On monotone solutions of some classes of difference equations. Discrete Dynamics in Nature and Society 2006, 2006:-9.
Stević S: On positive solutions of a
 -th order difference equation. Applied Mathematics Letters 2006,19(5):427-431. 10.1016/j.aml.2005.05.014
-th order difference equation. Applied Mathematics Letters 2006,19(5):427-431. 10.1016/j.aml.2005.05.014Stević S: Asymptotics of some classes of higher-order difference equations. Discrete Dynamics in Nature and Society 2007, 2007:-20.
Stević S: Existence of nontrivial solutions of a rational difference equation. Applied Mathematics Letters 2007,20(1):28-31. 10.1016/j.aml.2006.03.002
Stević S: Nontrivial solutions of higher-order rational difference equations. Matematicheskie Zametki 2008,84(5):772-780.
Sun T: On non-oscillatory solutions of the recursive sequence
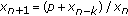 . Journal of Difference Equations and Applications 2005,11(6):483-485. 10.1080/10236190512331319343
. Journal of Difference Equations and Applications 2005,11(6):483-485. 10.1080/10236190512331319343Voulov HD: Existence of monotone solutions of some difference equations with unstable equilibrium. Journal of Mathematical Analysis and Applications 2002,272(2):555-564. 10.1016/S0022-247X(02)00173-7
Nguyen HT, Walker EA: A First Course in Fuzzy Logic. CRC Press, Boca Raton, Fla, USA; 1997:viii+266.
Wu C, Zhang B: Embedding problem of noncompact fuzzy number space
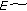 . I. Fuzzy Sets and Systems 1999,105(1):165-169. 10.1016/S0165-0114(97)00218-2
. I. Fuzzy Sets and Systems 1999,105(1):165-169. 10.1016/S0165-0114(97)00218-2Klir GJ, Yuan B: Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, Upper Saddle River, NJ, USA; 1995:xvi+574.
Bede B, Tanali GB: Perspectives of Fuzzy Initial Value Problems, Research Reports Series. University of Texas at El Paso; 2006.
Diamond P, Kloeden P: Metric Spaces of Fuzzy Sets: Theory and Application. World Scientific, River Edge, NJ, USA; 1994:x+178.
Román-Flores H, Barros LC, Bassanezi RC: A note on Zadeh's extensions. Fuzzy Sets and Systems 2001,117(3):327-331. 10.1016/S0165-0114(98)00408-4
Papaschinopoulos G, Stefanidou G: Boundedness and asymptotic behavior of the solutions of a fuzzy difference equation. Fuzzy Sets and Systems 2003,140(3):523-539. 10.1016/S0165-0114(03)00034-4
Acknowledgment
The authors would like to thank the referees for their helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Stefanidou, G., Papaschinopoulos, G. & Schinas, C. On an Exponential-Type Fuzzy Difference Equation. Adv Differ Equ 2010, 196920 (2010). https://doi.org/10.1155/2010/196920
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/196920
 is normal;
is normal; is fuzzy convex;
is fuzzy convex; is upper semicontinuous;
is upper semicontinuous; is compact, and
is compact, and  is a continuous and nondecreasing function in
is a continuous and nondecreasing function in  for each
for each  .
. is normal, that is, there exists an
is normal, that is, there exists an  such that
such that 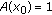 ;
;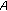 is fuzzy convex, that is for
is fuzzy convex, that is for 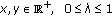 ;
; 
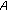 is upper semicontinuous
is upper semicontinuous ,
,  is compact.
is compact. is nondecreasing and left continuous;
is nondecreasing and left continuous;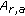 is nonincreasing and left continuous;
is nonincreasing and left continuous; .
.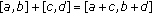 ,
, 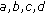 positive real numbers,
positive real numbers, ,
,  positive real numbers,
positive real numbers,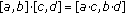 ,
, 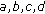 positive real numbers.
positive real numbers. is a positive fuzzy number which belongs to
is a positive fuzzy number which belongs to 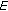 , with
, with 
 is a positive fuzzy number which belongs to
is a positive fuzzy number which belongs to  , with
, with 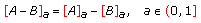
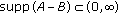 ;
; is a positive fuzzy number which belongs to
is a positive fuzzy number which belongs to  , with
, with 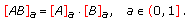



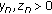 ,
, 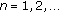 .
. 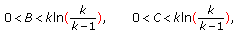
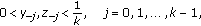
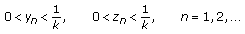
 .
.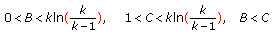
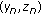 of system (1.7) we have that
of system (1.7) we have that 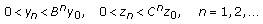
 tends to the unique zero equilibrium
tends to the unique zero equilibrium  of (1.7) as
of (1.7) as 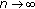 .
.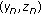 tends to the nonnegative equilibrium
tends to the nonnegative equilibrium  ,
, 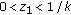 of (1.7) as
of (1.7) as 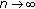 .
.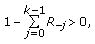


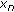 of the fuzzy difference equation (1.6) with initial values
of the fuzzy difference equation (1.6) with initial values 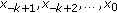 .
.
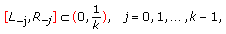
 of the fuzzy difference equation (1.6) with initial values
of the fuzzy difference equation (1.6) with initial values 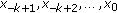 .
.
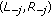 ,
,  has a positive solution
has a positive solution  such that (3.20) and
such that (3.20) and 


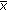 where
where
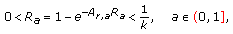
 hold.
hold.

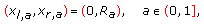
 ,
, 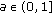 , is the unique function which satisfies (3.39).
, is the unique function which satisfies (3.39).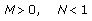
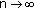 .
.
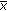 with respect to
with respect to  as
as  and converges to
and converges to 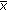 with respect to
with respect to  as
as 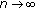 , where
, where  was defined by (3.38) and (3.39).
was defined by (3.38) and (3.39). . Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041
. Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041 . Taiwanese Journal of Mathematics 2002,6(3):405-414.
. Taiwanese Journal of Mathematics 2002,6(3):405-414. -th order difference equation. Applied Mathematics Letters 2006,19(5):427-431. 10.1016/j.aml.2005.05.014
-th order difference equation. Applied Mathematics Letters 2006,19(5):427-431. 10.1016/j.aml.2005.05.014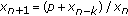 . Journal of Difference Equations and Applications 2005,11(6):483-485. 10.1080/10236190512331319343
. Journal of Difference Equations and Applications 2005,11(6):483-485. 10.1080/10236190512331319343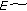 . I. Fuzzy Sets and Systems 1999,105(1):165-169. 10.1016/S0165-0114(97)00218-2
. I. Fuzzy Sets and Systems 1999,105(1):165-169. 10.1016/S0165-0114(97)00218-2