- Research Article
- Open access
- Published:
Positive Solutions for Impulsive Equations of Third Order in Banach Space
Advances in Difference Equations volume 2010, Article number: 185701 (2010)
Abstract
Using the fixed-point theorem, this paper is devoted to study the multiple and single positive solutions of third-order boundary value problems for impulsive differential equations in ordered Banach spaces. The arguments are based on a specially constructed cone. At last, an example is given to illustrate the main results.
1. Introduction
The purpose of this paper is to establish the existence of positive solutions for the following third-order three-point boundary value problems (BVP, for short) in Banach space 

where  ,
,  ,
,  ,
,  .
.  ,
,  ,
,  .
.  is the zero element of
is the zero element of  .
.
Recently, third-order boundary value problems (cf. [1–9]) have attracted many authors attention due to their wide range of applications in applied mathematics, physics, and engineering, especially in the bridge issue. To our knowledge, most papers in literature concern mainly about the existence of positive solutions for the cases in which the spaces are real and the equations have no parameters. And many authors consider nonlinear term have same linearity. In this paper, we consider the existence of solutions when the nonlinear terms have different properties, the space is abstract and the equations have two different parameters.
In [3], Guo et al. studied the following nonlinear three-point boundary value problem:

where  ,
,  . The authors obtained at least one positive solutions of BVP (1.2) by using fixed-point theorem when
. The authors obtained at least one positive solutions of BVP (1.2) by using fixed-point theorem when  is sublinear or suplinear.
is sublinear or suplinear.
In [8], Yao and Feng used the upper and lower solutions method proved some existence results for the following third-order two-point boundary value problem

Inspired by the above work, the aim of this paper is to establish some simple criteria for the existence of nontrivial solutions for BVP (1.1) under some weaker conditions. The new features of this paper mainly include the following aspects. Firstly, we consider the system (1.1) in abstract space while [3, 8] talk about equations in real space ( ). Secondly, we obtained the positive solutions when the two parameters have different ranges. Thirdly,
). Secondly, we obtained the positive solutions when the two parameters have different ranges. Thirdly,  and
and  in system (1.1) may have different properties. Fourthly,
in system (1.1) may have different properties. Fourthly,  in system (1.1) not only contains
in system (1.1) not only contains  but also
but also  , which is much more complicated. Finally, the main technique used here is the fixed-point theory and a special cone is constructed to study the existence of nontrivial solutions.
, which is much more complicated. Finally, the main technique used here is the fixed-point theory and a special cone is constructed to study the existence of nontrivial solutions.
We recall some basic facts about ordered Banach spaces  . The cone
. The cone  in
in  induces a partial order on
induces a partial order on  , that is,
, that is,  if and only if
if and only if  ,
,  is said to be normal if there exists a positive constant
is said to be normal if there exists a positive constant  such that
such that  implies
implies  , without loss of generality, suppose, in present paper, the normal constant
, without loss of generality, suppose, in present paper, the normal constant  .
.  denotes the measure of noncompactness (cf. [10]).
denotes the measure of noncompactness (cf. [10]).
Some preliminaries and a number of lemmas to the derivation of the main results are given in Section 2, then the proofs of the theorems are given in Section 3, followed by an example, in Section 4, to demonstrate the validity of our main results.
2. Preliminaries and Lemmas
In this paper we will consider the Banach space  , denote
, denote  and
and  ,
,  is continuous at
is continuous at  and
and  is left continuous at
is left continuous at  , the right limit
, the right limit  exists,
exists,  . For any
. For any  we define
we define  and
and  for
for  .
.
For convenience, let us list the following assumption.
(A) ,
,  ,
,  ,
,  . For any
. For any  and
and  ,
,  is relatively compact in
is relatively compact in  , where
, where  .
.
Lemma 2.1.
Assume that  , then for any
, then for any  , the following boundary value problem:
, the following boundary value problem:

has a unique solution

where

Proof.
The proof is similar to Lemma 2.2 in [3], we omit it.
Lemma 2.2 (see [3]).
Assume that  and
and  . Then
. Then  for any
for any  , where
, where  ,
,  .
.
Lemma 2.3 (see [3]).
Let  and
and  , then for any
, then for any  ,
,  , where
, where

In the paper, we define cone  as follows:
as follows:

Lemma 2.4 (see [10]).
Let  be a Banach space and
be a Banach space and  be a cone. Suppose
be a cone. Suppose  and
and  are bounded open sets,
are bounded open sets,  ,
,  ,
,  is completely continuous such that either
is completely continuous such that either
-
(i)
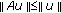 for any
for any 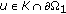 and
and 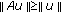 for any
for any 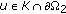 or
or -
(ii)
 for any
for any  and
and  for any
for any  .
.
Then  has a fixed-point in
has a fixed-point in  .
.
Lemma 2.5.
The vector  is a solution of differential systems (1.1) if and only if
is a solution of differential systems (1.1) if and only if  is the solution of the following integral systems:
is the solution of the following integral systems:

Define operators  ,
,  and
and  as follows:
as follows:

As we know, BVP (1.1) has a positive solution  if and only if
if and only if  is the fixed-point of
is the fixed-point of  .
.
Lemma 2.6.
 is completely continuous.
is completely continuous.
Proof.
By condition (A) we get  ,
,  , for all
, for all  . For any
. For any  , we have
, we have

Similarly

So  .
.
Next, we prove  is completely continuous. We first prove that
is completely continuous. We first prove that  is continuous. Let
is continuous. Let  and
and  such that
such that  . Let
. Let  , then
, then

By (A), we obtain

Hence

Since

By (2.11)–(2.13) and Lebesgue-dominated convergence theorem

So  is continuous. Similarly,
is continuous. Similarly,  is continuous. It follows that
is continuous. It follows that  is continuous.
is continuous.
Next we prove  is compact. Let
is compact. Let  be bounded,
be bounded,  and
and  . Let
. Let  for some
for some  , then
, then  ,
,  . It is easy to see that
. It is easy to see that  is equicontinuous. By condition (A) we have
is equicontinuous. By condition (A) we have

which implies that  . So,
. So,  , it follows that
, it follows that  is compact. The lemma is proved.
is compact. The lemma is proved.
In this paper, denote

where  or
or  ,
,  and
and  .
.  is a dual cone of
is a dual cone of  .
.
We list the assumptions:
(H1)  ,
,  , where
, where  ;
;
(H2)  ,
,  ,
,  , where
, where  and
and  ;
;
(H3)  ,
,  ,
,  ,
,  , where
, where  and
and  .
.
For convenience, denote

3. Main Results
Theorem 3.1.
Assume that (A), (H1) and the following condition (H)' hold, then BVP (1.1) has at least two positive solution while  and
and  .
.
(H)': ;
;  ;
;  , where
, where  ,
,  .
.
Proof.
Let  , then for
, then for  , we have
, we have

that is,

Similarly

So

Hence

Since  , there exist
, there exist  and
and  such that
such that  for
for  and
and  . Let
. Let  . Then for any
. Then for any  , by (H1) and the definition of
, by (H1) and the definition of  , we obtain
, we obtain

By (3.6) and (H)'

Similarly, by  , there exist
, there exist  and
and  such that
such that  for
for  and
and  with
with  . Let
. Let  . Then for any
. Then for any  ,
,

So we have by (3.8) and (H)'

By (3.5), (3.7), (3.9) and Lemma 2.4 we get that BVP (1.1) has at least two positive solutions with  .
.
Corollary 3.2.
Assume that (A) and the following condition hold, then the conclusion of Theorem 3.1 also holds.

Theorem 3.3.
Assume that (A) and (H2) hold, then BVP (1.1) has at least one positive solution when  and
and  .
.
Proof.
By Lemma 2.6, we see that  is completely continuous. By (H2), there exists
is completely continuous. By (H2), there exists  ,
,  ,
,  such that for
such that for  ,
,

for any  with
with  , where
, where  ,
,  such that
such that

Let  . Then for any
. Then for any  , we obtain
, we obtain

Similarly

It follows that

which implies

On the other hand, by  , there exists
, there exists  ,
,  such that
such that  for
for  and
and  . Let
. Let  ,
,  . For any
. For any  , we have
, we have

By the definition of  we get
we get

So

Hence

Therefore

By (3.16), (3.21) and Lemma 2.4, it is easily seen that  has a fixed-point
has a fixed-point  .
.
Corollary 3.4.
Let (A) and the following conditions hold, then BVP (1.1) has at least one positive solution while  and
and  .
.

Theorem 3.5.
Let (A) and (H3) hold, then BVP (1.1) has at least one positive solution while  and
and  .
.
Proof.
Since  , we choose
, we choose  ,
,  such that
such that  for
for  and
and  . Let
. Let  . Then for any
. Then for any  ,
,

So

which implies

On the other hand, by  and
and  , there exist
, there exist  ,
,  ,
,  such that
such that  and
and

where  satisfies
satisfies

Let  and
and  . Then for any
. Then for any  , we have
, we have

Similarly

Hence

So

By (3.25), (3.31), and Lemma 2.4,  has a fixed-point
has a fixed-point  .
.
Corollary 3.6.
Assume that (A) and the following conditions hold, then BVP (1.1) has at least one positive solution while  and
and  .
.

4. An Example
In this section, we construct an example to demonstrate the application of our main results obtained in Section 3. Consider the following third-order boundary value problem:

Conclusion.
BVP(4.1) has at least one positive solution.
Proof.
 ,
,  ,
,  . Define
. Define  .
.  ,
,  .
.  ,
,  .
.  , we know that
, we know that  , let
, let  , then for any
, then for any  ,
,  . It is easy to see that (A) is satisfied. On the other hand,
. It is easy to see that (A) is satisfied. On the other hand,

that is,  . Similarly,
. Similarly,  , it is easy to see that
, it is easy to see that  , where
, where  ,
,  . In this example,
. In this example,  ,
,  ,
,  and
and

and  .
.
Let  . By computing, we get
. By computing, we get

Above all, the conditions of Theorem 3.3 are satisfied. Then for any  and
and  , BVP (4.1) has at least one positive solution.
, BVP (4.1) has at least one positive solution.
References
Du Z, Ge W, Lin X: Existence of solutions for a class of third-order nonlinear boundary value problems. Journal of Mathematical Analysis and Applications 2004,294(1):104-112. 10.1016/j.jmaa.2004.02.001
Feng Y, Liu S: Solvability of a third-order two-point boundary value problem. Applied Mathematics Letters 2005,18(9):1034-1040. 10.1016/j.aml.2004.04.016
Guo L-J, Sun J-P, Zhao Y-H: Existence of positive solutions for nonlinear third-order three-point boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):3151-3158. 10.1016/j.na.2007.03.008
Gupta CP: Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equation. Journal of Mathematical Analysis and Applications 1992,168(2):540-551. 10.1016/0022-247X(92)90179-H
Ma R: Multiplicity results for a third order boundary value problem at resonance. Nonlinear Analysis: Theory, Methods & Applications 1998,32(4):493-499. 10.1016/S0362-546X(97)00494-X
Sun Y: Positive solutions of singular third-order three-point boundary value problem. Journal of Mathematical Analysis and Applications 2005,306(2):589-603. 10.1016/j.jmaa.2004.10.029
Webb JRL: Positive solutions of some three point boundary value problems via fixed point index theory. Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4319-4332. 10.1016/S0362-546X(01)00547-8
Yao Q, Feng Y: The existence of solution for a third-order two-point boundary value problem. Applied Mathematics Letters 2002,15(2):227-232. 10.1016/S0893-9659(01)00122-7
Yao Q: The existence and multiplicity of positive solutions for a third-order three-point boundary value problem. Acta Mathematicae Applicatae Sinica 2003,19(1):117-122. 10.1007/s10255-003-0087-1
Guo D: Nonlinear Functional Analysis. Shangdong Science and Technology Press, Jinan, China; 1985.
Acknowledgments
The author thanks Professor Liu and Professor Lou for many useful discussions and helpful suggestions. The work was partially supported by NSFC (10971155) and Innovation program of Shanghai Municipal Education Commission (09ZZ33).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cai, J. Positive Solutions for Impulsive Equations of Third Order in Banach Space. Adv Differ Equ 2010, 185701 (2010). https://doi.org/10.1155/2010/185701
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/185701
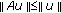 for any
for any 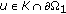 and
and 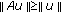 for any
for any 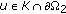 or
or for any
for any  and
and  for any
for any  .
.