- Research Article
- Open access
- Published:
On Type of Periodicity and Ergodicity to a Class of Fractional Order Differential Equations
Advances in Difference Equations volume 2010, Article number: 179750 (2010)
Abstract
We study several types of periodicity to a class of fractional order differential equations.
1. Introduction
Fractional order differential equations is a very important subject matter. These orders can be complex in viewpoint of pure mathematics. During the last few decades fractional order differential equations have emerged vigorously (cf., [1–8]). We observe that there is much interest in developing the qualitative theory of such equations. Indeed, this has been strongly motivated by their natural and widespread applicability in several fields of sciences and technology. Many real phenomena in those fields can be described very successfully by models using mathematical tools of fractional calculus, such as dielectric polarization, electrode-electrolyte polarization, electromagnetic wave, modeling of earthquake, fluid dynamics, traffic model with fractional derivative, measurement of viscoelastic material properties, modeling of viscoplasticity, Control Theory, and economy (cf., [3, 4, 9–15]). Very recently, some basic theory for initial value problem of fractional differential equations involving the Riemann-Liouville differential operators was discussed by Benchohra et al. [16], Agarwal et al. [17–19], Lakshmikantham [20], and Lakshmikantham and Vatsala [21, 22]. Mophou and N'Guérékata [23] have studied existence of mild solution for fractional semilinear differential equations with nonlocal conditions (more details can be found in [24–29]). El-Sayed and Ibrahim [30] and Benchohra et al. [31] initiated the study of fractional multivalued differential inclusions. In this direction, we refer to the article by Henderson and Ouahab [32] concerning the existence of solutions to fractional functional differential inclusions with finite delay, and existence of solutions for these types of equations in the infinite delay framework (see [16, 31]). In the case that fractional order is  , existence results for fractional boundary value problems of differential inclusions were studied by Ouahab [33].
, existence results for fractional boundary value problems of differential inclusions were studied by Ouahab [33].
We study in this work some sufficient conditions for the existence and uniqueness of pseudo-almost periodic mild solutions to the following semilinear fractional differential equation:

where  ,
,  is a linear densely defined operator of sectorial type on a complex Banach space
is a linear densely defined operator of sectorial type on a complex Banach space  and
and  is a pseudo-almost periodic function (see Definition 2.10) satisfying suitable conditions in
is a pseudo-almost periodic function (see Definition 2.10) satisfying suitable conditions in  . The fractional derivative is understood in the Riemann-Liouville sense. Type (1.1) equations are attracting increasing interest. For example, anomalous diffusion in fractals by Eidelman and Kochubei [10] or in macroeconomics by Ahn and McVinisch [1] has been recently studied in the setting of fractional differential equations like (1.1). The study of almost automorphic mild solutions of (1.1) was studied by Cuevas and Lizama in [34] (see also [35]).
. The fractional derivative is understood in the Riemann-Liouville sense. Type (1.1) equations are attracting increasing interest. For example, anomalous diffusion in fractals by Eidelman and Kochubei [10] or in macroeconomics by Ahn and McVinisch [1] has been recently studied in the setting of fractional differential equations like (1.1). The study of almost automorphic mild solutions of (1.1) was studied by Cuevas and Lizama in [34] (see also [35]).
As for almost periodic functions, pseudo-almost periodic functions have many applications in several problems, for example, in theory of functional differential equations, integral equations, and partial differential equations. The concept of pseudo-almost periodic was introduced by Zhang [36–39] in the early nineties. Since then, such notion became of great interest to several mathematicians (see [40–49]). To the knowledge of the authors, no results yet exist for pseudo-almost periodic mild solution of (1.1).
We also discuss sufficient conditions for the existence and uniqueness of an asymptotically almost periodic mild solution of the fractional Cauchy problem


In a work by Cuevas and de Souza [50] the authors proved existence and uniqueness of an S-asymptotically  -periodic solution of problem (1.2)-(1.3) (see also [51]). On the other hand, we give results on existence and uniqueness of an asymptotically almost automorphic mild solution to a class of fractional integrodifferential neutral equations.
-periodic solution of problem (1.2)-(1.3) (see also [51]). On the other hand, we give results on existence and uniqueness of an asymptotically almost automorphic mild solution to a class of fractional integrodifferential neutral equations.
We now turn to a summary of this work. The second section provides the definitions and preliminaries results to be used in theorems stated and proved in this article. In particular, we review some of the standard properties of the solution operator generated by a sectorial operator (see Proposition 2.2). We also recall the notion of almost periodicity, asymptotically almost periodicity, asymptotically almost automorphy, and pseudo-almost periodicity. In the third section, we obtain very general results on the existence of pseudo-almost periodic mild solution to equation (1.1). The fourth section is concerned with the existence of an asymptotically almost periodic mild solution to problem (1.2)-(1.3). While in the fifth section we use the machinery developed in the previous sections to obtain new results on existence and uniqueness of an asymptotically almost automorphic solution to a class of fractional integrodifferential neutral equation. To build intuition and throw some light on the power of our results and methods, we give, in the sixth section, a few applications.
2. Preliminaries and Basic Results
Let  and
and  be two Banach spaces. The notation
be two Banach spaces. The notation  and
and  stand for the collection of all continuous functions from
stand for the collection of all continuous functions from  into
into  and the Banach space of all bounded continuous functions from
and the Banach space of all bounded continuous functions from  into
into  endowed with the uniform convergence topology, respectively. Similarly,
endowed with the uniform convergence topology, respectively. Similarly,  and
and  stand, respectively, for the class of all jointly continuous functions from
stand, respectively, for the class of all jointly continuous functions from  into
into  and the collection of all jointly bounded continuous functions from
and the collection of all jointly bounded continuous functions from  into
into  . The notation
. The notation  stands for the space of bounded linear operators from
stands for the space of bounded linear operators from  into
into  endowed with the uniform operator topology, and we abbreviate it to
endowed with the uniform operator topology, and we abbreviate it to  whenever
whenever  . We set
. We set  for the closed ball with center at
for the closed ball with center at  radius
radius  in the space
in the space  . A closed and linear operator
. A closed and linear operator  is said to be sectorial of type
is said to be sectorial of type  if there exist
if there exist  ,
,  and
and  such that its resolvent exists outside the sector
such that its resolvent exists outside the sector  and
and  ,
,  . Sectorial operators are well studied in the literature. For a recent reference including several examples and properties we refer the reader to [52]. In order to give an operator theoretical approach, we recall the following definition (cf., [50, 51]).
. Sectorial operators are well studied in the literature. For a recent reference including several examples and properties we refer the reader to [52]. In order to give an operator theoretical approach, we recall the following definition (cf., [50, 51]).
Definition 2.1.
Let  be a closed and linear operator with domain
be a closed and linear operator with domain  defined on a Banach space
defined on a Banach space  . Recall
. Recall  the generator of a solution operator if there exist
the generator of a solution operator if there exist  and a strongly continuous function
and a strongly continuous function  such that
such that  and
and  ,
,  ,
,  . In this case,
. In this case,  is called the solution operator generated by
is called the solution operator generated by  .
.
We note that if  is sectorial of type
is sectorial of type  with
with  , then
, then  is the generator of a solution operator given by
is the generator of a solution operator given by  , where
, where  is a suitable path lying outside the sector
is a suitable path lying outside the sector  (cf., Cuesta's paper [53]). Very recently, Cuesta [53, Theorem
(cf., Cuesta's paper [53]). Very recently, Cuesta [53, Theorem  ] has proved that if
] has proved that if  is a sectorial operator of type
is a sectorial operator of type  for some
for some  and
and  then there exists
then there exists  such that
such that

Note that  is, in fact, integrable. The concept of a solution operator, as defined above, is closely related to the concept of a resolvent family (see Prüss [54, Chapter 1]). For the scalar case, where there is a large bibliography, we refer the reader to the monography by Gripenberg et al. [55] and references therein. Because of the uniqueness of the Laplace transform, in the border case
is, in fact, integrable. The concept of a solution operator, as defined above, is closely related to the concept of a resolvent family (see Prüss [54, Chapter 1]). For the scalar case, where there is a large bibliography, we refer the reader to the monography by Gripenberg et al. [55] and references therein. Because of the uniqueness of the Laplace transform, in the border case  the family
the family  corresponds to a
corresponds to a  -semigroup, whereas in the case
-semigroup, whereas in the case  a solution operator corresponds to the concept of a cosine family; see Arendt et al. [56] and Fattorini [57]. We note that solution operators, as well as resolvent families, are a particular case of
a solution operator corresponds to the concept of a cosine family; see Arendt et al. [56] and Fattorini [57]. We note that solution operators, as well as resolvent families, are a particular case of  -regularized families introduced by Lizama [58]. According to [58] a solution operator
-regularized families introduced by Lizama [58]. According to [58] a solution operator  corresponds to a
corresponds to a  -regularized family. The following result is a direct consequence of [58, Proposition
-regularized family. The following result is a direct consequence of [58, Proposition  and Lemma
and Lemma  ].
].
Proposition 2.2.
Let  be a solution operator on
be a solution operator on  with generator
with generator  . Then, one has the following.
. Then, one has the following.
-
(a)
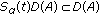 and
and 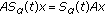 for all
for all 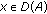 ,
, 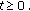
-
(b)
Let
 and
and 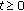 . Then
. Then 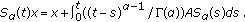
-
(c)
Let
 and
and 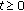 . Then
. Then 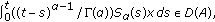

A characterization of generators of solution operators, analogous to the Hille-Yosida Theorem for  -semigroup, can be directly deduced from [58, Theorem
-semigroup, can be directly deduced from [58, Theorem  ]. Results on perturbation, approximation, representation as well as ergodic type theorems can be deduced from the more general context of
]. Results on perturbation, approximation, representation as well as ergodic type theorems can be deduced from the more general context of  -regularized resolvents (see [58–61]).
-regularized resolvents (see [58–61]).
Let us recall the notions of almost periodicity, asymptotically almost periodicity, asymptotically almost automorphy, and pseudo-almost periodicity which shall come into play later on.
Definition 2.3 (see [62]).
Let  be a Banach space. Then
be a Banach space. Then  is called almost periodic if
is called almost periodic if  is continuous, and for each
is continuous, and for each  there exists
there exists  such that for every interval of length
such that for every interval of length  it contains a number
it contains a number  with the property that
with the property that  for each
for each  . The number
. The number  above is called an
above is called an  -translation number for
-translation number for  , and the collection of such functions will be denoted by
, and the collection of such functions will be denoted by  .
.
Remark 2.4 (see [63]).
Note that each almost periodic function is bounded and uniformly continuous. It is well known that the range  of an almost periodic function
of an almost periodic function  is relatively compact.
is relatively compact.  endowed with the norm of uniform convergence on
endowed with the norm of uniform convergence on  is a Banach space.
is a Banach space.
Definition 2.5.
Let  and
and  be two Banach spaces. Then
be two Banach spaces. Then  is called almost periodic in
is called almost periodic in  uniformly for
uniformly for  if
if  is continuous, and for each
is continuous, and for each  and any compact
and any compact  there exists
there exists  such that every interval
such that every interval  of length
of length  it contains a number
it contains a number  with the property that
with the property that  for all
for all  ,
,  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
It is well known that the study of composition of two functions with special properties is important and basic for deep investigations. We begin with the following standard result in the theory of almost periodic function (see [39, 63]).
Lemma 2.6.
Let  and
and  . Then the function
. Then the function  .
.
Definition 2.7.
A continuous function  (resp.,
(resp.,  ) is called asymptotically almost periodic (resp., asymptotically almost periodic in
) is called asymptotically almost periodic (resp., asymptotically almost periodic in  uniformly in
uniformly in  ) if it admits a decomposition
) if it admits a decomposition  , where
, where  (resp.,
(resp.,  ) and
) and  (resp.,
(resp.,  ). Here
). Here  denotes the subspace of
denotes the subspace of  such that
such that  and
and  denotes the space of all continuous functions
denotes the space of all continuous functions  such that
such that  uniformly for
uniformly for  in any compact subset of
in any compact subset of  . Denote by
. Denote by  (resp.,
(resp.,  ) the set of all such functions.
) the set of all such functions.  is a Banach space with the sup norm.
is a Banach space with the sup norm.
Definition 2.8.
A continuous function  is called uniformly continuous on bounded sets uniformly for
is called uniformly continuous on bounded sets uniformly for  if for every
if for every  and every bounded subset
and every bounded subset  of
of  there exists
there exists  such that
such that  for all
for all  and all
and all  so that
so that  .
.
Lemma 2.9.
Let  and let
and let  be uniformly continuous on bounded sets uniformly for
be uniformly continuous on bounded sets uniformly for  . If
. If  , then
, then  .
.
Let  denote the space of all bounded continuous functions
denote the space of all bounded continuous functions  such that
such that

and  denotes the space of all continuous functions such that
denotes the space of all continuous functions such that  is bounded for all
is bounded for all  and
and

uniformly in  .
.
Definition 2.10 (see [36, 64]).
A function  (resp,
(resp,  ) is called pseudo-almost periodic (resp., pseudo-almost periodic in
) is called pseudo-almost periodic (resp., pseudo-almost periodic in  uniformly in
uniformly in  ) if
) if  where
where  (
( ) and
) and  (
( ).
).
The functions  and
and  are called the almost periodic component and, respectively, the ergodic perturbation of the function
are called the almost periodic component and, respectively, the ergodic perturbation of the function  . The set of all such functions will be denoted by
. The set of all such functions will be denoted by  (resp.,
(resp.,  ). Obviously
). Obviously  is a subspace of
is a subspace of  . Furthermore, we have that
. Furthermore, we have that  is a closed subspace of
is a closed subspace of  hence, it is a Banach space with the supremum norm (see [65]).
hence, it is a Banach space with the supremum norm (see [65]).
Lemma 2.11 (see [65]).
Let satisfy the following conditions.
satisfy the following conditions.
-
(i)
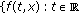 and
and  is bounded for every bounded subset
is bounded for every bounded subset  .
. -
(ii)
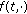 is uniformly continuous in each bounded subset of
is uniformly continuous in each bounded subset of 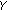 uniformly in
uniformly in  . More explicitly, given
. More explicitly, given 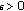 and
and 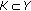 bounded, there exists
bounded, there exists 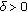 such that
such that 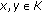 and
and 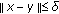 imply that
imply that 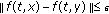 for all
for all 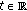 .
.
If  , then
, then  .
.
Lemma 2.12.
Assume that  is sectorial of type
is sectorial of type  . If
. If  is an almost periodic function and
is an almost periodic function and  is given by
is given by

then  .
.
Proof.
For  , we take
, we take  involved in Definition 2.3, then for every interval of length
involved in Definition 2.3, then for every interval of length  contains a number
contains a number  such that
such that  for each
for each  . The estimate
. The estimate

is responsible for the fact that  .
.
Lemma 2.13.
Assume that  is sectorial of type
is sectorial of type  . If
. If  is an asymptotically almost periodic function and
is an asymptotically almost periodic function and  is given by
is given by

then  .
.
Proof.
If  , where
, where  and
and  then we have that
then we have that  , where
, where


By the previous lemma  . Next, let us show that
. Next, let us show that  . Since
. Since  , for each
, for each  there exists a constant
there exists a constant  such that
such that  for all
for all  . Then for all
. Then for all  , we deduce
, we deduce

Therefore,  , that is,
, that is,  . This completes the proof.
. This completes the proof.
Lemma 2.14.
Assume that  is sectorial of type
is sectorial of type  . If
. If  is pseudo-almost periodic function and
is pseudo-almost periodic function and  is the function defined in (2.5). Then
is the function defined in (2.5). Then  .
.
Proof.
It is clear that  . In fact, we get
. In fact, we get  where
where  and
and  are given by (2.1). If
are given by (2.1). If  , where
, where  and
and  , then from Lemma 2.12,
, then from Lemma 2.12,  . To complete the proof, we show that
. To complete the proof, we show that  . For
. For  we see that
we see that

where  ,
,  .
.
It is not hard to check that  as
as  . Next, since
. Next, since  is bounded and
is bounded and  is integrable in
is integrable in  , using the Lebesgue dominated convergence theorem, it follows that
, using the Lebesgue dominated convergence theorem, it follows that  . The proof is now completed.
. The proof is now completed.
Let  be a continuous function such that
be a continuous function such that  as
as  . We consider the space
. We consider the space  endowed with the norm
endowed with the norm 
Lemma 2.15 (see [66]).
A subset  is a relatively compact set if it verifies the following conditions.
is a relatively compact set if it verifies the following conditions.
(c-1) The set  is relatively compact in
is relatively compact in  for each
for each  .
.
(c-2) The set  is equicontinuous.
is equicontinuous.
(c-3) For each  there exists
there exists  such that
such that  for all
for all  and all
and all  .
.
Let  be a continuous function such that
be a continuous function such that  as
as  . Consider the space
. Consider the space  endowed with the norm
endowed with the norm 
Lemma 2.16 (see [67]).
A subset  is a relatively compact set if it verifies the following conditions.
is a relatively compact set if it verifies the following conditions.
(c-1) The set  is relatively compact in
is relatively compact in  for all
for all  .
.
(c-2)  uniformly for all
uniformly for all  .
.
Definition 2.17.
A continuous function  is called almost automorphic if for every sequence of real numbers
is called almost automorphic if for every sequence of real numbers  there exists a subsequence
there exists a subsequence  such that
such that  is well defined for each
is well defined for each  , and
, and  for each
for each  . Denote by
. Denote by  the set of all such functions; it constitutes a Banach space when it is endowed with the sup norm.
the set of all such functions; it constitutes a Banach space when it is endowed with the sup norm.
Almost automorphic functions were introduced by Bochner [68] as a natural generalization of the concept of almost periodic function. A complete description of the properties and further applications to evolution equations can be found in the monographs [69] and [70] by N'Guérékata.
Definition 2.18.
Let  and
and  be two Banach spaces. A continuous function
be two Banach spaces. A continuous function  is called almost automorphic in
is called almost automorphic in  uniformly for
uniformly for  in compact subsets of
in compact subsets of  if for every compact subset
if for every compact subset  of
of  and every real sequence
and every real sequence  there exists a subsequence
there exists a subsequence  such that
such that  is well defined for each
is well defined for each  ,
,  and
and  for each
for each  ,
,  . Denote by
. Denote by  the set of all such functions.
the set of all such functions.
Lemma 2.19 (see [34]).
Assume that  is sectorial of type
is sectorial of type  . If
. If  is an almost automorphic function and
is an almost automorphic function and  is given by (2.5), then
is given by (2.5), then  .
.
In 1980s, N'Guérékata [71] defined asymptotically almost automorphic functions as perturbation of almost automorphic functions by functions vanishing at infinite. Since then, those functions have generated lots of developments and applications; we refer the reader to [69, 72–74] and the references therein.
Definition 2.20 (see [75]).
A continuous function  (resp.,
(resp.,  ) is called asymptotically almost automorphic (asymptotically almost automorphic in
) is called asymptotically almost automorphic (asymptotically almost automorphic in  uniformly for
uniformly for  in compact subsets of
in compact subsets of  ) if it admits a decomposition
) if it admits a decomposition  ,
,  , where
, where  (resp.,
(resp.,  ) and
) and  (resp.,
(resp.,  ). Denote by
). Denote by  (resp.,
(resp.,  ) the set of all such functions.
) the set of all such functions.  is a Banach space with the sup norm (see [75, Lemma
is a Banach space with the sup norm (see [75, Lemma  ]). We note that the range of an asymptotically almost automorphic function is relatively compact [75].
]). We note that the range of an asymptotically almost automorphic function is relatively compact [75].
Lemma 2.21.
Assume that  is sectorial of type
is sectorial of type  . If
. If  is an asymptotically almost automorphic function and
is an asymptotically almost automorphic function and  is given by (2.7), then
is given by (2.7), then  .
.
Proof.
 , where
, where  and
and  . We have that
. We have that  , where
, where  and
and  are the functions given by (2.8) and (2.9), respectively. By previous lemma
are the functions given by (2.8) and (2.9), respectively. By previous lemma  and by the proof of Lemma 2.13
and by the proof of Lemma 2.13 . This ends the proof.
. This ends the proof.
Lemma 2.22 (see [75]).
Let  and let
and let  be uniformly continuous on bounded sets uniformly for
be uniformly continuous on bounded sets uniformly for  . If
. If  , then
, then  .
.
3. Pseudo-Almost Periodic Mild Solutions
We recall the following definition that will be essential for us.
Definition 3.1 (see [34]).
Suppose that  generates an integrable solution operator
generates an integrable solution operator  . A continuous function
. A continuous function  satisfying the integral equation
satisfying the integral equation

is called a mild solution to the equation (1.1).
The following are the main results of this section.
Theorem 3.2.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be a function pseudo-almost periodic in
be a function pseudo-almost periodic in  , uniformly in
, uniformly in  and assume that there exists an integrable bounded function
and assume that there exists an integrable bounded function  satisfying
satisfying

Then equation (1.1) has a unique pseudo-almost periodic mild solution.
Proof.
We define the operator  by
by

Given  , in view of Lemma 2.11, we have that
, in view of Lemma 2.11, we have that  is a pseudo-almost periodic function, and hence bounded in
is a pseudo-almost periodic function, and hence bounded in  . Since the function
. Since the function  is integrable on
is integrable on  (
( ), we get that
), we get that  exists. Now, by Lemma 2.14, we obtain that
exists. Now, by Lemma 2.14, we obtain that  and hence
and hence  is well defined. It suffices to show that the operator
is well defined. It suffices to show that the operator  has a unique fixed point in
has a unique fixed point in  . For this, consider
. For this, consider  . We can deduce that
. We can deduce that

where  . Since
. Since  for
for  sufficiently large, by the contraction principle,
sufficiently large, by the contraction principle,  has a unique fixed point
has a unique fixed point  . This completes the proof.
. This completes the proof.
We can establish the following existence result.
Proposition 3.3.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be a function pseudo-almost periodic in
be a function pseudo-almost periodic in  uniformly in
uniformly in  that satisfies the Lipschitz condition (3.2) with
that satisfies the Lipschitz condition (3.2) with  . Let
. Let  . If
. If  , where
, where  and
and  are the constants in (2.1), then equation (1.1) has a unique pseudo-almost periodic mild solution.
are the constants in (2.1), then equation (1.1) has a unique pseudo-almost periodic mild solution.
Proof.
Let  be the map defined in the previous theorem. For
be the map defined in the previous theorem. For  we can estimate that
we can estimate that

which finishes the proof.
Corollary 3.4.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be a function pseudo-almost periodic in
be a function pseudo-almost periodic in  uniformlies in
uniformlies in  that satisfy the Lipschitz condition
that satisfy the Lipschitz condition

If  , where
, where  and
and  are the constants given in (2.1), then equation (1.1) has a unique pseudo-almost periodic mild solution.
are the constants given in (2.1), then equation (1.1) has a unique pseudo-almost periodic mild solution.
To establish our next result we consider perturbations  of (1.1) that satisfy the following boundedness condition.
of (1.1) that satisfy the following boundedness condition.
(H1) There exists a continuous nondecreasing function  such that
such that  for all
for all  and
and  .
.
We have the following result.
Theorem 3.5.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be a function pseudo-almost periodic in
be a function pseudo-almost periodic in  uniformly in
uniformly in  that satisfies assumption (H1) and the following conditions.
that satisfies assumption (H1) and the following conditions.
(H2)  is uniformly continuous on bounded subset of
is uniformly continuous on bounded subset of  uniformly in
uniformly in  .
.
(H3) For each  ,
,  , where
, where  is given by Lemma 2.15. Set
is given by Lemma 2.15. Set

where  and
and  are constants given in (2.1).
are constants given in (2.1).
(H4) For each  there is
there is  such that, for every
such that, for every  ,
,  implies that
implies that

for all  .
.
(H5) For all  ,
,  , and
, and  , the set
, the set  is relatively compact in
is relatively compact in  .
.
(H6)  .
.
Then equation (1.1) has a pseudo-almost periodic mild solution.
Proof.
We define the operator  on
on  as in (3.3). We show that
as in (3.3). We show that  has a fixed point in
has a fixed point in  .
.
-
(1)
For
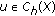 , we have that
, we have that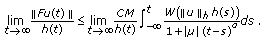 (3.9)
(3.9)
It follows from condition (H3) that  . From condition (H4) it follows that
. From condition (H4) it follows that  is a continuous map.
is a continuous map.
-
(ii)
We next show that
 is completely continuous. The argument comes from Lemma 2.15. In fact, let
is completely continuous. The argument comes from Lemma 2.15. In fact, let 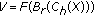 and
and  for
for 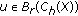 . Initially, we will prove that
. Initially, we will prove that  is a relatively compact subset of
is a relatively compact subset of 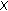 for each
for each  . It follows from condition (H3) that the function
. It follows from condition (H3) that the function  is integrable on
is integrable on  . Hence, for
. Hence, for  , we can choose
, we can choose 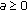 such that
such that 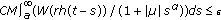 . Hence
. Hence 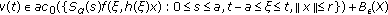 , where
, where 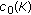 denotes the convex hull of
denotes the convex hull of 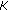 . Using that
. Using that 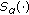 is strongly continuous and the property (H5), we infer that
is strongly continuous and the property (H5), we infer that 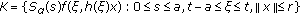 is relatively compact set, and
is relatively compact set, and 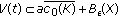 , which establishes our assertion.
, which establishes our assertion.We next show that the set
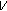 is equicontinuous. In fact, we can decompose
is equicontinuous. In fact, we can decompose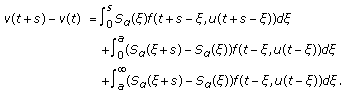 (3.10)
(3.10)For each
 , we can choose
, we can choose 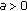 and
and 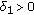 such that
such that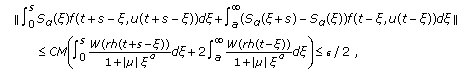 (3.11)
(3.11)
for  . Moreover, since
. Moreover, since  is relatively compact set and
is relatively compact set and  is strongly continuous, we can choose
is strongly continuous, we can choose  such that
such that  for
for  . Combining these estimates, we get
. Combining these estimates, we get  for
for  small enough and independent of
small enough and independent of  .
.
Finally, applying condition (H3), we can show that

and this convergence is independent of  . Taking into account Lemma 2.15,
. Taking into account Lemma 2.15,  is a relatively compact set in
is a relatively compact set in  .
.
-
(iii)
If
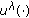 is a solution of equation
is a solution of equation  for some
for some 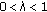 , then we can check that
, then we can check that 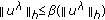 and, combining with condition (H6), we conclude that the set
and, combining with condition (H6), we conclude that the set 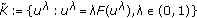 is bounded.
is bounded. -
(iv)
It follows, from Lemmas 2.11 and 2.14, that
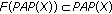 and, consequently,
and, consequently, 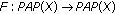 is completely continuous. Since
is completely continuous. Since 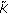 is bounded and using Leray-Schauder alternative theorem, we infer that
is bounded and using Leray-Schauder alternative theorem, we infer that 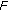 has a fixed point
has a fixed point  . Let
. Let  be a sequence in
be a sequence in 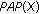 that converges to
that converges to  . We see that
. We see that 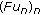 converges to
converges to  uniformly in
uniformly in 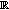 . This implies that
. This implies that  and completes the proof.
and completes the proof.
It is particularly interesting to note that the next result is not covered by the results by Cuevas and Lizama [34].
Corollary 3.6.
Assume that conditions (H1)–(H6) hold and that  is sectorial of type
is sectorial of type  . If
. If  is almost periodic in
is almost periodic in  uniformly for
uniformly for  , then equation (1.1) has an almost periodic mild solution.
, then equation (1.1) has an almost periodic mild solution.
Proof.
It is a consequence of Lemmas 2.6 and 2.12.
4. Asymptotically Almost Periodic Mild Solutions
We recall the following definition.
Definition 4.1 (see [50]).
Suppose that  generates an integrable solution operator
generates an integrable solution operator  . A function
. A function  satisfying
satisfying

is called a mild solution of the problem (1.2)-(1.3).
Theorem 4.2.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be a function asymptotically almost periodic in
be a function asymptotically almost periodic in  uniformly in
uniformly in  and assume that there exists an integrable bounded function
and assume that there exists an integrable bounded function  satisfying
satisfying

Then the problem (1.2)-(1.3) has a unique asymptotically almost periodic mild solution.
Proof.
We define the operator  on the space
on the space  by
by

We show initially that  . In fact, we observe that the estimate (2.1) implies that
. In fact, we observe that the estimate (2.1) implies that  . It follows from Lemma 2.9 that the function
. It follows from Lemma 2.9 that the function  is asymptotically almost periodic; then by Lemma 2.13,
is asymptotically almost periodic; then by Lemma 2.13,  and hence
and hence  is well defined. Let
is well defined. Let  be in
be in  and define
and define  . We have the following estimate:
. We have the following estimate:

which is responsible for the fact that  has a unique fixed point in
has a unique fixed point in  .
.
Corollary 4.3.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be a function asymptotically almost periodic in
be a function asymptotically almost periodic in  uniformly in
uniformly in  that satisfies the Lipschitz condition (4.2) with
that satisfies the Lipschitz condition (4.2) with  . If
. If  , where
, where  and
and  are the constants given in (2.1), then the problem (1.2)-(1.3) has a unique asymptotically almost periodic mild solution.
are the constants given in (2.1), then the problem (1.2)-(1.3) has a unique asymptotically almost periodic mild solution.
Taking  with
with  and
and  in (1.2), the above result produces the following corollary.
in (1.2), the above result produces the following corollary.
Corollary 4.4.
Let  be a function asymptotically almost periodic in
be a function asymptotically almost periodic in  uniformly in
uniformly in  that satisfies the Lipschitz condition (4.2) with
that satisfies the Lipschitz condition (4.2) with  . Then problem (1.2)-(1.3) has a unique asymptotically almost periodic solution whenever
. Then problem (1.2)-(1.3) has a unique asymptotically almost periodic solution whenever  .
.
Remark 4.5.
A similar result as that of the previous corollary was obtained by Cuevas and de Souza [50] for obtaining an S-asymptotically  -periodic mild solution for problem (1.2)-(1.3) (see [50, Remark 3.6] for complementary comments).
-periodic mild solution for problem (1.2)-(1.3) (see [50, Remark 3.6] for complementary comments).
Next, we establish a version of Theorem 4.2 which enable us to consider locally Lipschitz perturbations for equation (1.2). We have the following result.
Theorem 4.6.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be a function asymptotically almost periodic in
be a function asymptotically almost periodic in  uniformly in
uniformly in  and assume that there is a continuous and nondecreasing function
and assume that there is a continuous and nondecreasing function  such that for each positive number
such that for each positive number  , and
, and  ,
,  ,
,  , one has
, one has

where  and
and  for
for  ; then there is
; then there is  such that for each
such that for each  with
with  there exists a unique asymptotically almost periodic mild solution of (1.2)-(1.3).
there exists a unique asymptotically almost periodic mild solution of (1.2)-(1.3).
Proof.
Let  and
and  be such that
be such that  . We affirm that the assertion holds for
. We affirm that the assertion holds for  . In fact, we consider
. In fact, we consider  such that
such that  . We set
. We set

endowed with the metric  . We define the operator
. We define the operator  on the space
on the space  by (4.3). Let
by (4.3). Let  we next show that
we next show that  We have the estimate
We have the estimate  that is,
that is,  .
.
On the other hand, for  we obtain
we obtain

To conclude, we note that  , which means that
, which means that  is a
is a  -contraction. This completes the proof.
-contraction. This completes the proof.
Theorem 4.7.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be an asymptotically almost periodic in
be an asymptotically almost periodic in  uniformly in
uniformly in  that satisfies the following conditions.
that satisfies the following conditions.
(H*1) There is a continuous nondecreasing function  such that
such that  for all
for all  and
and  .
.
(H*2)  is uniformly continuous on bounded sets of
is uniformly continuous on bounded sets of  uniformly in
uniformly in  .
.
(H*3) For each  ,
,  , where
, where  is given by Lemma 2.16. Set
is given by Lemma 2.16. Set

where  and
and  are constants given in (2.1).
are constants given in (2.1).
(H*4) For each  there is
there is  such that, for every
such that, for every  ,
,  implies that
implies that

for all  .
.
(H*5) For all  , and
, and  , the set
, the set  is relatively compact in
is relatively compact in  .
.
(H*6)  .
.
Then problem (1.2)-(1.3) has an asymptotically almost periodic mild solution.
Proof.
We define the operator  on
on  as in (4.3). We show that
as in (4.3). We show that  has a fixed point in
has a fixed point in  .
.
-
(i)
For
 , we have that
, we have that (4.10)
(4.10)It follows from (H*3) that
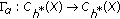 . From condition (H*4) it follows that
. From condition (H*4) it follows that 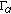 is a continuous map.
is a continuous map. -
(ii)
We next show that
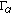 is completely continuous. Let
is completely continuous. Let 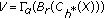 and
and 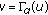 for
for  . Initially, we can infer that
. Initially, we can infer that 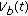 is a relatively compact subset of
is a relatively compact subset of 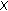 for each
for each 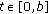 . In fact, using condition (H*5) we get that
. In fact, using condition (H*5) we get that 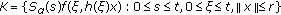 is relatively compact. It is easy to see that
is relatively compact. It is easy to see that 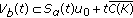 , which establishes our assertion. From the decomposition of
, which establishes our assertion. From the decomposition of  given by
given by  , it follows that the set
, it follows that the set  is equicontinuous. We can show that
is equicontinuous. We can show that  uniformly for all
uniformly for all 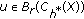 . From Lemma 2.16, we deduce that
. From Lemma 2.16, we deduce that 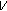 is relatively compact set in
is relatively compact set in  .
.
We note that the set  is bounded. In fact, it follows from condition (H*6) and the estimate
is bounded. In fact, it follows from condition (H*6) and the estimate  . It follows, from Lemmas 2.9 and 2.13, that
. It follows, from Lemmas 2.9 and 2.13, that  . The remaining of proof makes use of a similar argument already done in the proof of Theorem 3.5.
. The remaining of proof makes use of a similar argument already done in the proof of Theorem 3.5.
5. Asymptotically Almost Automorphic Solutions of Fractional Integro Differential Neutral Equations
This section is mainly concerned with the existence and uniqueness of an asymptotically almost automorphic mild solution to the fractional integro differential neutral equation

where  ,
,  is a linear densely defined operator of sectorial type, and
is a linear densely defined operator of sectorial type, and  are functions subject to some additional conditions.
are functions subject to some additional conditions.
Definition 5.1.
Suppose that  generates an integrable solution operator
generates an integrable solution operator  . A function
. A function  satisfying the integral equation
satisfying the integral equation

is called a mild solution of problem (5.1).
We have the following result.
Theorem 5.2.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be two functions asymptotically almost automorphic in
be two functions asymptotically almost automorphic in  uniformly for
uniformly for  in compact subsets of
in compact subsets of  such that
such that

If  , where
, where  and
and  are the constants given in (2.1), then problem (5.1) has a unique asymptotically almost automorphic mild solution.
are the constants given in (2.1), then problem (5.1) has a unique asymptotically almost automorphic mild solution.
Proof.
We define the operator  on the space
on the space  by
by

Applying Lemma 2.22, we infer that  and
and  belong to
belong to  . By Lemma 2.21, we obtain that
. By Lemma 2.21, we obtain that  is
is  -valued. Furthermore, we have the estimate
-valued. Furthermore, we have the estimate

which proves that  is a contraction we conclude that
is a contraction we conclude that  has a unique fixed point in
has a unique fixed point in  . This completes the proof.
. This completes the proof.
Next, we establish a local version of the previous result.
Theorem 5.3.
Assume that  is sectorial of type
is sectorial of type  . Let
. Let  be two functions asymptotically almost automorphic in
be two functions asymptotically almost automorphic in  uniformly for
uniformly for  in compact subsets of
in compact subsets of  and assume that there are continuous and nondecreasing functions
and assume that there are continuous and nondecreasing functions  such that for each positive number
such that for each positive number  , and
, and  ,
,  ,
,  , one has
, one has

for all  , where
, where  and
and  for every
for every  . Then there is
. Then there is  such that
such that  satisfies
satisfies  then there is a unique asymptotically almost automorphic mild solution of (5.1).
then there is a unique asymptotically almost automorphic mild solution of (5.1).
Proof.
Let  and
and  be such that
be such that

where  and
and  are the constants given in (2.1). We consider
are the constants given in (2.1). We consider  such that
such that  , with
, with  ; we define the space
; we define the space  endowed with the metric
endowed with the metric  . We also define the operator
. We also define the operator  on the space
on the space  by (5.4). Let
by (5.4). Let  be in
be in  in a similar way as that of proof of Theorem 5.2; we have that
in a similar way as that of proof of Theorem 5.2; we have that  . Moreover, we obtain the estimate
. Moreover, we obtain the estimate

Therefore  . On the other hand, for
. On the other hand, for  , we see that
, we see that

which shows that  is a contraction from
is a contraction from  into
into  . The assertion is now a consequence of the contraction mapping principle.
. The assertion is now a consequence of the contraction mapping principle.
Remark 5.4.
A similar result was obtained by Diagana et al. [76] for the existence of asymptotically almost automorphic solutions to some abstract partial neutral integrodifferential equations.
Theorem 5.5.
Assume that  is sectorial of type
is sectorial of type  and that conditions (H*1),(H*3), (H*4) and (H*5) hold. In addition, suppose that the following properties hold.
and that conditions (H*1),(H*3), (H*4) and (H*5) hold. In addition, suppose that the following properties hold.
(A1) The functions  are asymptotically almost automorphic in
are asymptotically almost automorphic in  and uniformly for
and uniformly for  in compact subsets of
in compact subsets of  and uniformly continuous on bounded sets of
and uniformly continuous on bounded sets of  uniformly in
uniformly in  .
.
(A2) There is a constant  such that
such that  for all
for all  and
and  (here
(here  is given in Lemma 2.16). Set
is given in Lemma 2.16). Set

where  and
and  are the constants given in (2.1).
are the constants given in (2.1).
(A3)  .
.
Then problem (5.1) has an asymptotically almost automorphic mild solution.
Proof.
We define the operator  on
on  as in (5.4); we consider the decomposition
as in (5.4); we consider the decomposition  , where
, where

For  , we have that
, we have that

Hence  is
is  -valued. On the other hand,
-valued. On the other hand,  is an
is an  -contraction. It follows from the proof of the Theorem 4.7 that
-contraction. It follows from the proof of the Theorem 4.7 that  is completely continuous. From Lemmas 2.21 and 2.22, we have that
is completely continuous. From Lemmas 2.21 and 2.22, we have that

Hence  and
and  is completely continuous. Putting
is completely continuous. Putting  we claim that there is
we claim that there is  such that
such that  . In fact, if we assume that this assertion is false, then for all
. In fact, if we assume that this assertion is false, then for all  we can choose
we can choose  and
and  such that
such that  . We observe that
. We observe that

Thus  ), which is contrary to assumption (A3). We have that
), which is contrary to assumption (A3). We have that  is a contraction on
is a contraction on  and
and  is a compact set. It follows from [77, Corollary
is a compact set. It follows from [77, Corollary  ] that
] that  has a fixed point
has a fixed point  . More precisely,
. More precisely,  , and this finishes the proof.
, and this finishes the proof.
6. Applications
To illustrate our results, initially we examine sufficient conditions for the existence and uniqueness of pseudo-almost periodic mild solutions to the fractional relaxation-oscillation equation given by


where  . To study this system in the abstract form (1.1), we choose the space
. To study this system in the abstract form (1.1), we choose the space  and the operator
and the operator  defined by
defined by  , with domain
, with domain  . It is well known that
. It is well known that  is generator of an analytic semigroup on
is generator of an analytic semigroup on  . Hence,
. Hence,  is sectorial of type
is sectorial of type  . (6.1) can be formulated by the inhomogeneous problem (1.1), where
. (6.1) can be formulated by the inhomogeneous problem (1.1), where  . Let us consider the nonlinearity
. Let us consider the nonlinearity  for all
for all  and
and  ,
,  with
with  ,
,  . We observe that
. We observe that  . Hence
. Hence  . We observe that
. We observe that  is pseudo-almost periodic in
is pseudo-almost periodic in  , uniformly in
, uniformly in  such that (3.6) holds for
such that (3.6) holds for  . If we assume that
. If we assume that  , then by Corollary 3.4, the fractional relaxation-oscillation equation (6.1) has a unique pseudo-almost periodic mild solution.
, then by Corollary 3.4, the fractional relaxation-oscillation equation (6.1) has a unique pseudo-almost periodic mild solution.
Taking  and
and  , we define the function
, we define the function  as
as

We consider the following fractional relaxation-oscillation equation given by

Equation (6.4) can be expressed as an abstract equation of the form (1.1), where

Proposition 6.1.
Problem (6.4) has a pseudo-almost periodic mild solution.
Proof.
Let us briefly discuss the proof of this proposition. We get without difficulties the following two estimates:

which are responsible for the fact that  and that
and that  is uniformly continuous on bounded sets of
is uniformly continuous on bounded sets of  uniformly in
uniformly in  .
.
It is straightforward to verify that

and  . Hence, we can define
. Hence, we can define  in (H1) by
in (H1) by  . Taking
. Taking  ,
,  ;
;  . From the discussion above, we see that
. From the discussion above, we see that

which means that conditions (H3) and (H4) of Theorem 3.5 are satisfied. An easy computation leads to  . An argument involving Simon's theorem (see [78, Theorem
. An argument involving Simon's theorem (see [78, Theorem  , pages 71–74]) proves that the set
, pages 71–74]) proves that the set  is relatively compact in
is relatively compact in  . In fact, we can verify that
. In fact, we can verify that  ,
,  . Hence, for
. Hence, for  ,
,  is bounded uniformly in
is bounded uniformly in  and
and  . On the other hand, we can infer the following estimate:
. On the other hand, we can infer the following estimate:

Therefore,

uniformly in  and
and  . Finally, Simon's theorem leads to the conclusion that
. Finally, Simon's theorem leads to the conclusion that  is relatively compact. Using Theorem 3.5, equation (6.4) has a pseudo-almost periodic mild solution.
is relatively compact. Using Theorem 3.5, equation (6.4) has a pseudo-almost periodic mild solution.
Next, we examine the existence and uniqueness of an asymptotically almost automorphic mild solution to the fractional differential equation

where  ,
,  are appropriate functions, and
are appropriate functions, and  . From Corollary 4.3, we can deduce the following result.
. From Corollary 4.3, we can deduce the following result.
Proposition 6.2.
Assume that  is an asymptotically almost periodic function and that there exists a constant
is an asymptotically almost periodic function and that there exists a constant  such that
such that  for all
for all  . If
. If  , then (6.11) has a unique asymptotically almost periodic mild solution.
, then (6.11) has a unique asymptotically almost periodic mild solution.
We consider the fractional differential equation



From Theorem 4.6, we deduce the following result.
Proposition 6.3.
Assume that  is an asymptotically almost periodic function, then there is
is an asymptotically almost periodic function, then there is  such that for each
such that for each  with
with  there exists a unique asymptotically almost periodic mild solution of (6.12)–(6.14).
there exists a unique asymptotically almost periodic mild solution of (6.12)–(6.14).
Proof.
The proof is straightforward. Indeed, (6.12) can be expressed as an abstract equation of form (1.2), where  ,
,  ,
,  . We observe that
. We observe that  , for all
, for all  and
and  . Hence the perturbation is locally Lipschitz. We remark that
. Hence the perturbation is locally Lipschitz. We remark that  is asymptotically almost periodic in
is asymptotically almost periodic in  uniformly in
uniformly in  , as we mentioned before, by using Theorem 4.6.
, as we mentioned before, by using Theorem 4.6.
Take  and
and  . We define the function
. We define the function  by
by

We examine asymptotically almost periodic mild solution to the fractional relaxation-oscillation equation given by

where  .
.
Proposition. 6.4
Problem (6.16) has an asymptotically almost periodic mild solution.
Proof.
We briefly recall some argument of the proof. Problem (6.16) can be written as an abstract problem of the form (1.2)-(1.3) in  , where the perturbation associated is
, where the perturbation associated is

We can choose the function  in (H*1) by
in (H*1) by  . From the estimate
. From the estimate

we get conditions (H*2) and (H*4), the latter being considered with  ,
,  .
.
We can infer that

Hence condition (H*3) is fulfilled. By looking at the estimates

and using Simon's theorem, we conclude that condition (H*5) holds. Consequently, by Theorem 4.7 we can assert that problem (6.16) has an asymptotically almost periodic mild solution. This completes the proof of Proposition 6.4.
Remark 6.5.
It is easy to check that results in Section 5 are applicable to similar fractional differential equations as those treated in this section. For the sake of shortness, the details are left to the reader.
References
Anh VV, Mcvinish R: Fractional differential equations driven by Lévy noise. Journal of Applied Mathematics and Stochastic Analysis 2003,16(2):97-119. 10.1155/S1048953303000078
Gorenflo R, Mainardi F: Fractional calculus: integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics, CISM Courses and Lectures. Volume 378. Edited by: Carpinteri A, Mainardi F. Springer, Vienna, Austria; 1997:223-276.
Hilfer R (Ed): Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Hu T, Wang Y: Numerical detection of the lowest "efficient dimensions" for chaotic fractional differential systems. Open Mathematics Journal 2008, 1: 11-18. 10.2174/1874117700801010011
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:xvi+523.
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Podlubny I: Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and some of Their Application, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives. Theory and Applications. Gordon and Breach Science, Yverdon, France; 1993:xxxvi+976.
Diethelm K, Freed AD: On the solution of nonlinear fractional order equations used in the modeling of viscoplasticity. In Scientific Computing in Chemical Engineering II-Computational Fluid Dynamics, Reaction Engineering and Molecular Properties. Edited by: Keil F, Mackens W, Voss H, Werther J. Springer, Heidelberg, Germany; 1999:217-224.
Eidelman SD, Kochubei AN: Cauchy problem for fractional diffusion equations. Journal of Differential Equations 2004,199(2):211-255. 10.1016/j.jde.2003.12.002
Lin W: Global existence theory and chaos control of fractional differential equations. Journal of Mathematical Analysis and Applications 2007,332(1):709-726. 10.1016/j.jmaa.2006.10.040
Oustalup A: Systéms Asservis D'ordre Fractionaire. Éditions Masson; 1983.
Oustalup A: La Dérivation non Entière: Théorie, Synthèse, Applications, Série Automatique. Editions Hermès; 1995.
Podlubny I, Petráš I, Vinagre BM, O'Leary P, Dorčák L: Analogue realizations of fractional-order controllers. Fractional order calculus and its applications. Nonlinear Dynamics 2002,29(1–4):281-296. 10.1023/A:1016556604320
Ross B (Ed): Fractional Calculus and Its Applications, Lecture Notes in Mathematics, vol. 457. Springer, Berlin, Germany; 1975:vi+381.
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: Existence results for fractional order functional differential equations with infinite delay. Journal of Mathematical Analysis and Applications 2008,338(2):1340-1350. 10.1016/j.jmaa.2007.06.021
Agarwal RP, Benchohra M, Hamani S: A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions. to appear in Acta Applicandae Mathematicae
Agarwal RP, Benchohra M, Hamani S: Boundary value problems for fractional differential equations. Georgian Mathematical Journal 2009,16(3):401-411.
Agarwal RP, Belmekki M, Benchohra M: A survey on semilinear differential equations and inclusions involving Riemann-Liouville fractional derivative. Advances in Difference Equations 2009, 2009:-47.
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Lakshmikantham V, Vatsala AS: Theory of fractional differential inequalities and applications. Communications in Applied Analysis 2007,11(3-4):395-402.
Mophou GM, N'Guérékata GM: Mild solutions for semilinear fractional differential equations. Electronic Journal of Differential Equations 2009, (21):1-9.
El-Borai MM: Some probability densities and fundamental solutions of fractional evolution equations. Chaos, Solitons and Fractals 2002,14(3):433-440. 10.1016/S0960-0779(01)00208-9
El-Borai MM: Semigroups and some nonlinear fractional differential equations. Applied Mathematics and Computation 2004,149(3):823-831. 10.1016/S0096-3003(03)00188-7
El-Borai MM: The fundamental solutions for fractional evolution equations of parabolic type. Journal of Applied Mathematics and Stochastic Analysis 2004, (3):197-211. 10.1155/S1048953304311020
Mophou GM, Nakoulima O, N'Guérékata GM: Existence results for some fractional differential equations with nonlocal conditions. submitted
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
N'Guérékata GM: A Cauchy problem for some fractional abstract differential equation with non local conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):1873-1876. 10.1016/j.na.2008.02.087
El-Sayed AMA, Ibrahim A-G: Multivalued fractional differential equations. Applied Mathematics and Computation 1995,68(1):15-25. 10.1016/0096-3003(94)00080-N
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: Existence results for fractional functional differential inclusions with infinite delay and applications to control theory. Fractional Calculus & Applied Analysis 2008,11(1):35-56.
Henderson J, Ouahab A: Fractional functional differential inclusions with finite delay. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):2091-2105. 10.1016/j.na.2008.02.111
Ouahab A: Some results for fractional boundary value problem of differential inclusions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3877-3896. 10.1016/j.na.2007.10.021
Cuevas C, Lizama C: Almost automorphic solutions to a class of semilinear fractional differential equations. Applied Mathematics Letters 2008,21(12):1315-1319. 10.1016/j.aml.2008.02.001
Cuevas C, Lizama C: Almost automorphic solutions to integral equations on the line. Semigroup Forum 2009,79(3):461-472. 10.1007/s00233-009-9154-0
Zhang CY: Pseudo-almost-periodic solutions of some differential equations. Journal of Mathematical Analysis and Applications 1994,181(1):62-76. 10.1006/jmaa.1994.1005
Zhang CY: Integration of vector-valued pseudo-almost periodic functions. Proceedings of the American Mathematical Society 1994,121(1):167-174. 10.1090/S0002-9939-1994-1186140-8
Zhang CY: Pseudo almost periodic solutions of some differential equations. II. Journal of Mathematical Analysis and Applications 1995,192(2):543-561. 10.1006/jmaa.1995.1189
Zhang C: Almost Periodic Type Functions and Ergodicity. Science Press, Beijing, China; 2003:xii+355.
Ait Dads E, Arino O: Exponential dichotomy and existence of pseudo almost-periodic solutions of some differential equations. Nonlinear Analysis: Theory, Methods & Applications 1996,27(4):369-386. 10.1016/0362-546X(95)00027-S
Ait Dads E, Ezzinbi K, Arino O: Pseudo almost periodic solutions for some differential equations in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 1997,28(7):1141-1155. 10.1016/S0362-546X(97)82865-9
Amir B, Maniar L: Composition of pseudo-almost periodic functions and Cauchy problems with operator of nondense domain. Annales Mathématiques Blaise Pascal 1999,6(1):1-11. 10.5802/ambp.110
Cuevas C, Hernández M E: Pseudo-almost periodic solutions for abstract partial functional differential equations. Applied Mathematics Letters 2009,22(4):534-538. 10.1016/j.aml.2008.06.026
Cuevas C, Pinto M: Existence and uniqueness of pseudo almost periodic solutions of semilinear Cauchy problems with non dense domain. Nonlinear Analysis: Theory, Methods & Applications 2001,45(1):73-83. 10.1016/S0362-546X(99)00330-2
Diagana T: Pseudo almost periodic solutions to some differential equations. Nonlinear Analysis: Theory, Methods & Applications 2005,60(7):1277-1286. 10.1016/j.na.2004.11.002
Diagana T, Mahop CM, N'Guérékata GM: Pseudo-almost-periodic solutions to some semilinear differential equations. Mathematical and Computer Modelling 2006,43(1-2):89-96. 10.1016/j.mcm.2005.04.013
Diagana T, Mahop CM, N'Guérékata GM, Toni B: Existence and uniqueness of pseudo-almost periodic solutions to some classes of semilinear differential equations and applications. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2442-2453. 10.1016/j.na.2005.08.024
Diagana T, Mahop CM: Pseudo almost periodic solutions to a neutral delay integral equation. Cubo 2007,9(1):47-55.
Diagana T: Existence of pseudo almost periodic solutions to some classes of partial hyperbolic evolution equations. Electronic Journal of Qualitative Theory of Differential Equations 2007, (3):12.
Cuevas C, de Souza JC:
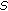 -asymptotically
-asymptotically  -periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013
-periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013Cuevas C, de Souza JC:Existence of
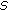 -asymptotically
-asymptotically  -periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007
-periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007Haase M: The Functional Calculus for Sectorial Operators, Operator Theory: Advances and Applications. Volume 169. Birkhäuser, Basel, Switzerland; 2006:xiv+392.
Cuesta E: Asymptotic behaviour of the solutions of fractional integro-differential equations and some time discretizations. Discrete and Continuous Dynamical Systems 2007, 277-285.
Prüss J: Evolutionary Integral Equations and Applications, Monographs in Mathematics. Volume 87. Birkhäuser, Basel, Switzerland; 1993:xxvi+366.
Gripenberg G, Londen S-O, Staffans O: Volterra Integral and Functional Equations, Encyclopedia of Mathematics and Its Applications. Volume 34. Cambridge University Press, Cambridge, UK; 1990:xxii+701.
Arendt W, Batty CJK, Hieber M, Neubrander F: Vector-Valued Laplace Transforms and Cauchy Problems, Monographs in Mathematics. Volume 96. Birkhäuser, Basel, Switzerland; 2001:xii+523.
Fattorini O: Second Order Differential Equations in Banach Spaces, North-Holland Mathematics Studies. Volume 108. North-Holland, Amsterdam, The Netherlands; 1985.
Lizama C:On approximation and representation of
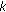 -regularized resolvent families. Integral Equations and Operator Theory 2001,41(2):223-229. 10.1007/BF01295306
-regularized resolvent families. Integral Equations and Operator Theory 2001,41(2):223-229. 10.1007/BF01295306Lizama C, Prado H: Rates of approximation and ergodic limits of regularized operator families. Journal of Approximation Theory 2003,122(1):42-61. 10.1016/S0021-9045(03)00040-6
Lizama C, Sánchez J:On perturbation of
 -regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.
-regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.Shaw S-Y, Chen J-C:Asymptotic behavior of
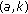 -regularized resolvent families at zero. Taiwanese Journal of Mathematics 2006,10(2):531-542.
-regularized resolvent families at zero. Taiwanese Journal of Mathematics 2006,10(2):531-542.Zaidman S: Almost-Periodic Functions in Abstract Spaces, Research Notes in Mathematics. Volume 126. Pitman, Boston, Mass, USA; 1985:iii+133.
Fink AM: Almost Periodic Differential Equations, Lecture Notes in Mathematics, vol. 377. Springer, Berlin, Germany; 1974:viii+336.
Zhang C: Pseudo almost periodic functions and their applications, thesis. The University of Western Ontario; 1992.
Li H-X, Huang F-L, Li J-Y: Composition of pseudo almost-periodic functions and semilinear differential equations. Journal of Mathematical Analysis and Applications 2001,255(2):436-446. 10.1006/jmaa.2000.7225
Henríquez HR, Lizama C: Compact almost automorphic solutions to integral equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):6029-6037. 10.1016/j.na.2009.05.042
Cuevas C, Henríquez H: Solutions of second order abstract retarded functional differential equations on the line. submitted
Bochner S: Continuous mappings of almost automorphic and almost periodic functions. Proceedings of the National Academy of Sciences of the United States of America 1964, 52: 907-910. 10.1073/pnas.52.4.907
N'Guérékata GM: Topics in Almost Automorphy. Springer, New York, NY, USA; 2005:xii+168.
N'Guérékata GM: Almost Automorphic and Almost Periodic Functions in Abstract Spaces. Kluwer Academic Publishers/Plenum Press, New York, NY, USA; 2001:x+138.
N'Guérékata GM: Quelques remarques sur les fonctions asymptotiquement presque automorphes. Les Annales des Sciences Mathématiques du Québec 1983,7(2):185-191.
Bugajewski D, N'Guérékata GM: On the topological structure of almost automorphic and asymptotically almost automorphic solutions of differential and integral equations in abstract spaces. Nonlinear Analysis: Theory, Methods & Applications 2004,59(8):1333-1345.
Diagana T, N'Guérékata GM: Almost automorphic solutions to some classes of partial evolution equations. Applied Mathematics Letters 2007,20(4):462-466. 10.1016/j.aml.2006.05.015
Diagana T, N'Guérékata GM, Minh NV: Almost automorphic solutions of evolution equations. Proceedings of the American Mathematical Society 2004,132(11):3289-3298. 10.1090/S0002-9939-04-07571-9
Ding H-S, Xiao T-J, Liang J: Asymptotically almost automorphic solutions for some integrodifferential equations with nonlocal initial conditions. Journal of Mathematical Analysis and Applications 2008,338(1):141-151. 10.1016/j.jmaa.2007.05.014
Diagana T, Hernández EM, dos Santos JPC: Existence of asymptotically almost automorphic solutions to some abstract partial neutral integro-differential equations. Nonlinear Analysis: Theory, Methods & Applications 2009,71(1-2):248-257. 10.1016/j.na.2008.10.046
Martin, RH Jr.: Nonlinear Operators and Differential Equations in Banach Spaces. Robert E. Krieger, Melbourne, Fla, USA; 1987:xiv+440.
Simon J: Compact sets in the space
 . Annali di Matematica Pura ed Applicata. Serie Quarta 1987, 146: 65-96.
. Annali di Matematica Pura ed Applicata. Serie Quarta 1987, 146: 65-96.
Acknowledgment
Claudio Cuevas is partially supported by CNPQ/Brazil under Grant no. 300365/2008-0.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R., Andrade, B. & Cuevas, C. On Type of Periodicity and Ergodicity to a Class of Fractional Order Differential Equations. Adv Differ Equ 2010, 179750 (2010). https://doi.org/10.1155/2010/179750
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/179750
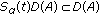 and
and 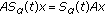 for all
for all 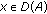 ,
, 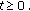
 and
and 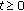 . Then
. Then 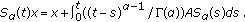
 and
and 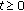 . Then
. Then 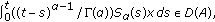
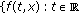 and
and  is bounded for every bounded subset
is bounded for every bounded subset  .
.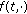 is uniformly continuous in each bounded subset of
is uniformly continuous in each bounded subset of 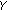 uniformly in
uniformly in  . More explicitly, given
. More explicitly, given 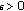 and
and 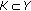 bounded, there exists
bounded, there exists 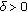 such that
such that 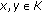 and
and 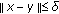 imply that
imply that 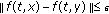 for all
for all 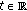 .
.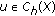 , we have that
, we have that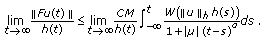
 is completely continuous. The argument comes from Lemma 2.15. In fact, let
is completely continuous. The argument comes from Lemma 2.15. In fact, let 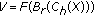 and
and  for
for 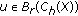 . Initially, we will prove that
. Initially, we will prove that  is a relatively compact subset of
is a relatively compact subset of  for each
for each  . It follows from condition (H3) that the function
. It follows from condition (H3) that the function  is integrable on
is integrable on  . Hence, for
. Hence, for  , we can choose
, we can choose  such that
such that 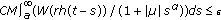 . Hence
. Hence 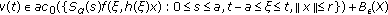 , where
, where 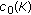 denotes the convex hull of
denotes the convex hull of 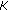 . Using that
. Using that 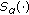 is strongly continuous and the property (H5), we infer that
is strongly continuous and the property (H5), we infer that 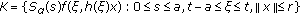 is relatively compact set, and
is relatively compact set, and 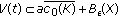 , which establishes our assertion.
, which establishes our assertion.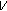 is equicontinuous. In fact, we can decompose
is equicontinuous. In fact, we can decompose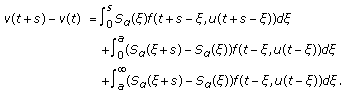
 , we can choose
, we can choose 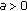 and
and 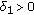 such that
such that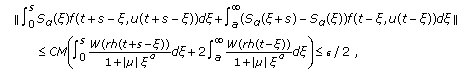
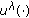 is a solution of equation
is a solution of equation  for some
for some 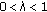 , then we can check that
, then we can check that 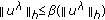 and, combining with condition (H6), we conclude that the set
and, combining with condition (H6), we conclude that the set 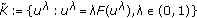 is bounded.
is bounded.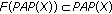 and, consequently,
and, consequently, 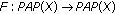 is completely continuous. Since
is completely continuous. Since 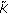 is bounded and using Leray-Schauder alternative theorem, we infer that
is bounded and using Leray-Schauder alternative theorem, we infer that 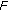 has a fixed point
has a fixed point  . Let
. Let  be a sequence in
be a sequence in 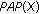 that converges to
that converges to  . We see that
. We see that 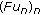 converges to
converges to  uniformly in
uniformly in 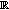 . This implies that
. This implies that  and completes the proof.
and completes the proof. , we have that
, we have that
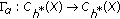 . From condition (H*4) it follows that
. From condition (H*4) it follows that 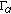 is a continuous map.
is a continuous map.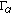 is completely continuous. Let
is completely continuous. Let 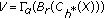 and
and 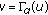 for
for  . Initially, we can infer that
. Initially, we can infer that 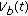 is a relatively compact subset of
is a relatively compact subset of 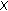 for each
for each 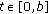 . In fact, using condition (H*5) we get that
. In fact, using condition (H*5) we get that 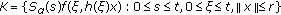 is relatively compact. It is easy to see that
is relatively compact. It is easy to see that 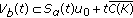 , which establishes our assertion. From the decomposition of
, which establishes our assertion. From the decomposition of  given by
given by  , it follows that the set
, it follows that the set  is equicontinuous. We can show that
is equicontinuous. We can show that  uniformly for all
uniformly for all 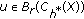 . From Lemma 2.16, we deduce that
. From Lemma 2.16, we deduce that 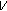 is relatively compact set in
is relatively compact set in  .
. -asymptotically
-asymptotically  -periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013
-periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013 -asymptotically
-asymptotically  -periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007
-periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007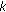 -regularized resolvent families. Integral Equations and Operator Theory 2001,41(2):223-229. 10.1007/BF01295306
-regularized resolvent families. Integral Equations and Operator Theory 2001,41(2):223-229. 10.1007/BF01295306 -regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.
-regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.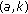 -regularized resolvent families at zero. Taiwanese Journal of Mathematics 2006,10(2):531-542.
-regularized resolvent families at zero. Taiwanese Journal of Mathematics 2006,10(2):531-542. . Annali di Matematica Pura ed Applicata. Serie Quarta 1987, 146: 65-96.
. Annali di Matematica Pura ed Applicata. Serie Quarta 1987, 146: 65-96.