- Research Article
- Open access
- Published:
A Study on the 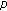 -Adic Integral Representation on
-Adic Integral Representation on 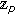 Associated with Bernstein and Bernoulli Polynomials
Associated with Bernstein and Bernoulli Polynomials
Advances in Difference Equations volume 2010, Article number: 163217 (2010)
Abstract
We consider the Bernstein polynomials on  and investigate some interesting properties of Bernstein polynomials related to Stirling numbers and Bernoulli numbers.
and investigate some interesting properties of Bernstein polynomials related to Stirling numbers and Bernoulli numbers.
1. Introduction
Let  denote the set of continuous function on
denote the set of continuous function on  . Then, Bernstein operator for
. Then, Bernstein operator for  is defined as
is defined as

for  , where
, where  is called Bernstein polynomial of degree
is called Bernstein polynomial of degree  . Some researchers have studied the Bernstein polynomials in the area of approximation theory (see [1–6]).
. Some researchers have studied the Bernstein polynomials in the area of approximation theory (see [1–6]).
Let  be a fixed prime number. Throughout this paper
be a fixed prime number. Throughout this paper  ,
,  ,
,  , and
, and  will, respectively, denote the ring of
will, respectively, denote the ring of  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers, the complex number field, and the completion of algebraic closure of
-adic rational numbers, the complex number field, and the completion of algebraic closure of  . Let
. Let  be the set of uniformly differentiable function on
be the set of uniformly differentiable function on  . For
. For  , the
, the  -adic
-adic  -integral on
-integral on  is defined by
is defined by

In the special case, if we set  in (1.2), we have
in (1.2), we have

In this paper, we consider Bernstein polynomials on  and we investigate some interesting properties of Bernstein polynomials related to Stirling numbers and Bernoulli numbers.
and we investigate some interesting properties of Bernstein polynomials related to Stirling numbers and Bernoulli numbers.
2. Bernstein Polynomials Related to Stirling Numbers and Bernoulli Numbers
In this section, for  , we consider Bernstein type operator on
, we consider Bernstein type operator on  as follows:
as follows:

for  , where
, where  is called Bernstein polynomial of degree
is called Bernstein polynomial of degree  . We consider Newton's forward difference operator as follows:
. We consider Newton's forward difference operator as follows:

For  ,
,

Then, we have

From (2.4), we note that

where

The Stirling number of the first kind is defined by

and the Stirling number of the second kind is also defined by

By (2.5), (2.6), (2.7), and (2.8), we see that

where  . Note that, for
. Note that, for  and
and  ,
,

Thus, we note that  is the generating function of Bernstein polynomial. It is easy to show that
is the generating function of Bernstein polynomial. It is easy to show that

By (2.11), we obtain the following theorem.
Theorem 2.1.
For  with
with  , one has
, one has

where  are the
are the  th Bernoulli numbers.
th Bernoulli numbers.
In [12], it is known that


for  . By (1.1) and (2.14), we see that
. By (1.1) and (2.14), we see that

for  . By (2.15), we obtain the following theorem.
. By (2.15), we obtain the following theorem.
Theorem 2.2.
For  , and
, and  , one has
, one has

From (2.13) and (2.14), we note that

In [16], it is known that

By (2.17), (2.18), and Theorem 2.2, we have

From the definition of the Stirling numbers of the first kind, we drive that

By (2.17), (2.19), and (2.20), we obtain the following theorem.
Theorem 2.3.
For  and
and  , one has
, one has

By Theorems 2.2 and 2.3, we obtain the following corollary.
Corollary 2.4.
For  , one has
, one has

where  are the
are the  th Bernoulli numbers.
th Bernoulli numbers.
References
Acikgoz M, Araci S: A study on the integral of the product of several type Bernstein polynomials. IST Transaction of Applied Mathematics-Modelling and Simulation. In press
Acikgoz M, Araci S: On the generating function of the Bernstein polynomials. In Proceedings of the 8th International Conference of Numerical Analysis and Applied Mathematics (ICNAAM '10), March 2010, Rhodes, Greece. AIP;
Bernstein S: Demonstration du theoreme de Weierstrass, fondee sur le calcul des probabilities. Communications of the Kharkov Mathematical Society 1913, 13: 1-2.
Kim T, Jang LC, Yi H: A note on the modified q -Bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12.
Phillips GM: Bernstein polynomials based on the q -integers. Annals of Numerical Mathematics 1997,4(1–4):511-518.
Kim MS, Kim D, Kim T: On the q-Euler numbers related to modified q-Bernstein polynomials. http://arxiv.org/abs/1007.3317
Kim T: q -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
Kim T: q -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
Kim T: Note on the Euler q -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
Kim T: On a q -analogue of the p -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
Kim T: Barnes-type multiple q -zeta functions and q -Euler polynomials. Journal of Physics A 2010.,43(25):
Kim T: Power series and asymptotic series associated with the q -analog of the two-variable p -adic L -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
Kim T, Choi J, Kim Y-H: Some identities on the q-Bernstein polynomials, g-Stirling numbers and q-Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010,20(3):335-341.
Kim T: Some identities on the q -Euler polynomials of higher order and q -Stirling numbers by the fermionic p -adic integral on
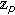 . Russian Journal of Mathematical Physics 2009,16(4):484-491. 10.1134/S1061920809040037
. Russian Journal of Mathematical Physics 2009,16(4):484-491. 10.1134/S1061920809040037Kim T: On p -adic interpolating function for q -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027
Kim T, Park D-W, Rim S-H: On multivariate p -adic q -integrals. Journal of Physics A 2001,34(37):7633-7638. 10.1088/0305-4470/34/37/315
Acknowledgment
The present investigation was supported by the Scientific Research Project Administration of Akdeniz University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jang, LC., Kim, WJ. & Simsek, Y. A Study on the 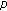 -Adic Integral Representation on
-Adic Integral Representation on 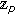 Associated with Bernstein and Bernoulli Polynomials.
Adv Differ Equ 2010, 163217 (2010). https://doi.org/10.1155/2010/163217
Associated with Bernstein and Bernoulli Polynomials.
Adv Differ Equ 2010, 163217 (2010). https://doi.org/10.1155/2010/163217
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/163217
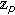 . Russian Journal of Mathematical Physics 2009,16(4):484-491. 10.1134/S1061920809040037
. Russian Journal of Mathematical Physics 2009,16(4):484-491. 10.1134/S1061920809040037