- Research Article
- Open access
- Published:
On the Existence of Locally Attractive Solutions of a Nonlinear Quadratic Volterra Integral Equation of Fractional Order
Advances in Difference Equations volume 2010, Article number: 127093 (2010)
Abstract
The authors employs a hybrid fixed point theorem involving the multiplication of two operators for proving an existence result of locally attractive solutions of a nonlinear quadratic Volterra integral equation of fractional (arbitrary) order. Investigations will be carried out in the Banach space of real functions which are defined, continuous, and bounded on the real half axis  .
.
1. Introduction
The theory of differential and integral equations of fractional order has recently received a lot of attention and now constitutes a significant branch of nonlinear analysis. Numerous research papers and monographs have appeared devoted to differential and integral equations of fractional order (cf., e.g., [1–6]). These papers contain various types of existence results for equations of fractional order.
In this paper, we study the existence of locally attractive solutions of the following nonlinear quadratic Volterra integral equation of fractional order:

for all  and
and  , in the space of real functions defined, continuous, and bounded on an unbounded interval.
, in the space of real functions defined, continuous, and bounded on an unbounded interval.
It is worthwhile mentioning that up to now integral equations of fractional order have only been studied in the space of real functions defined on a bounded interval. The result obtained in this paper generalizes several ones obtained earlier by many authors.
In fact, our result in this paper is motivated by the extension of the work of Hu and Yan [7]. Also, We proceed and generalize the results obtained in the papers [8, 9].
2. Notations, Definitions, and Auxiliary Facts
Denote by  the space of Lebesgue integrable functions on the interval
the space of Lebesgue integrable functions on the interval  , which is equipped with the standard norm. Let
, which is equipped with the standard norm. Let  and let
and let  be a fixed number. The Riemann-Liouville fractional integral of order
be a fixed number. The Riemann-Liouville fractional integral of order  of the function
of the function  is defined by the formula:
is defined by the formula:

where  denotes the gamma function.
denotes the gamma function.
It may be shown that the fractional integral operator,  transforms the space
transforms the space  into itself and has some other properties (see [10–12]).
into itself and has some other properties (see [10–12]).
Let  be the space of continuous and bounded real-valued functions on
be the space of continuous and bounded real-valued functions on  and let
and let  be a subset of
be a subset of  . Let
. Let  be an operator and consider the following operator equation in
be an operator and consider the following operator equation in  , namely,
, namely,

for all  . Below we give different characterizations of the solutions for the operator equation (2.2) on
. Below we give different characterizations of the solutions for the operator equation (2.2) on  . We need the following definitions in the sequel.
. We need the following definitions in the sequel.
Definition 2.1.
We say that solutions of (2.2) are locally attractive if there exists an  and an
and an  such that for all solutions
such that for all solutions  and
and  of (2.2) belonging to
of (2.2) belonging to  we have that:
we have that:

Definition 2.2.
An operator  is called Lipschitz if there exists a constant
is called Lipschitz if there exists a constant  such that
such that  for all
for all  . The constant
. The constant  is called the Lipschitz constant of
is called the Lipschitz constant of  on
on  .
.
Definition 2.3 (Dugundji and Granas [13]).
An operator  on a Banach space
on a Banach space  into itself is called compact if for any bounded subset
into itself is called compact if for any bounded subset  of
of  ,
,  is a relatively compact subset of
is a relatively compact subset of  . If
. If  is continuous and compact, then it is called completely continuous on
is continuous and compact, then it is called completely continuous on  .
.
We seek the solutions of (1.1) in the space  of continuous and bounded real-valued functions defined on
of continuous and bounded real-valued functions defined on  . Define a standard supremum norm
. Define a standard supremum norm  and a multiplication "
and a multiplication " " in
" in  by
by

Clearly,  becomes a Banach space with respect to the above norm and the multiplication in it. By
becomes a Banach space with respect to the above norm and the multiplication in it. By  we denote the space of Lebesgue integrable functions on
we denote the space of Lebesgue integrable functions on  with the norm
with the norm  defined by
defined by

We employ a hybrid fixed point theorem of Dhage [14] for proving the existence result.
Theorem 2.4 (Dhage [14]).
Let  be a closed-convex and bounded subset of the Banach space
be a closed-convex and bounded subset of the Banach space  and let
and let  be two operators satisfying:
be two operators satisfying:
-
(a)
 is Lipschitz with the Lipschitz constant
is Lipschitz with the Lipschitz constant  ,
, -
(b)
 is completely continuous,
is completely continuous, -
(c)
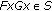 for all
for all  , and
, and -
(d)
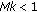 where
where  .
.
Then the operator equation

has a solution and the set of all solutions is compact in  .
.
3. Existence Result
We consider the following set of hypotheses in the sequel.
(H1) The function  is continuous, and there exists a bounded function
is continuous, and there exists a bounded function  with bound
with bound  satisfying
satisfying

for all  and
and  .
.
(H2) The function  defined by
defined by  is bounded with
is bounded with

(H3) The function  is continuous and
is continuous and  .
.
(H4) The function  is continuous. Moreover, there exist a function
is continuous. Moreover, there exist a function  being continuous on
being continuous on  and a function
and a function  being continuous on
being continuous on  with
with  and such that
and such that

for all  such that
such that  and for all
and for all  .
.
For further purposes let us define the function  by putting
by putting

Obviously the function  is continuous on
is continuous on  .
.
In what follows we will assume additionally that the following conditions are satisfied.
(H5) The functions  defined by the formulas
defined by the formulas

are bounded on  and vanish at infinity, that is,
and vanish at infinity, that is,  .
.
Remark 3.1.
Note that if the hypotheses  and
and  hold, then there exist constants
hold, then there exist constants  and
and  such that:
such that:

Theorem 3.2.
Assume that the hypotheses  hold. Furthermore, if
hold. Furthermore, if  , where
, where  and
and  are defined in Remark 3.1, then (1.1) has at least one solution in the space
are defined in Remark 3.1, then (1.1) has at least one solution in the space  . Moreover, solutions of (1.1) are locally attractive on
. Moreover, solutions of (1.1) are locally attractive on  .
.
Proof.
Set  . Consider the closed ball
. Consider the closed ball  in
in  centered at origin 0 and of radius
centered at origin 0 and of radius  , where
, where  .
.
Let us define two operators  and
and  on
on  by
by

for all  .
.
According to the hypothesis  , the operator
, the operator  is well defined and the function
is well defined and the function  is continuous and bounded on
is continuous and bounded on  . Also, since the function
. Also, since the function  is continuous on
is continuous on  , the function
, the function  is continuous and bounded in view of hypothesis
is continuous and bounded in view of hypothesis  . Therefore
. Therefore  and
and  define the operators
define the operators  . We will show that
. We will show that  and
and  satisfy the requirements of Theorem 2.4 on
satisfy the requirements of Theorem 2.4 on  .
.
The operator  is a Lipschitz operator on
is a Lipschitz operator on  . In fact, let
. In fact, let  be arbitrary. Then by hypothesis
be arbitrary. Then by hypothesis  , we get
, we get

for all  . Taking the supremum over
. Taking the supremum over  ,
,

for all  . This shows that
. This shows that  is a Lipschitz on
is a Lipschitz on  with the Lipschitz constant
with the Lipschitz constant  .
.
Next, we show that  is a continuous and compact operator on
is a continuous and compact operator on  . First we show that
. First we show that  is continuous on
is continuous on  . To do this, let us fix arbitrary
. To do this, let us fix arbitrary  and take
and take  such that
such that  . Then we get
. Then we get

Since  is continuous on
is continuous on  , then it is bounded on
, then it is bounded on  , and there exists a nonnegative constant, say
, and there exists a nonnegative constant, say  , such that
, such that  . Hence, in view of hypothesis
. Hence, in view of hypothesis  , we infer that there exists
, we infer that there exists  such that
such that  for
for  . Thus, for
. Thus, for  we derive that
we derive that

Furthermore, let us assume that  . Then, evaluating similarly to the above we obtain the following estimate:
. Then, evaluating similarly to the above we obtain the following estimate:

where  ,
,  ,
,  .
.
Therefore, from the uniform continuity of the function  on the set
on the set  we derive that
we derive that  as
as  . Hence, from the above-established facts we conclude that the operator
. Hence, from the above-established facts we conclude that the operator  maps the ball
maps the ball  continuously into itself.
continuously into itself.
Now, we show that  is compact on
is compact on  . It is enough to show that every sequence
. It is enough to show that every sequence  in
in  has a Cauchy subsequence. In view of hypotheses
has a Cauchy subsequence. In view of hypotheses  and
and  , we infer that:
, we infer that:

for all  . Taking the supremum over
. Taking the supremum over  , we obtain
, we obtain  for all
for all  . This shows that
. This shows that  is a uniformly bounded sequence in
is a uniformly bounded sequence in  . We show that it is also equicontinuous. Let
. We show that it is also equicontinuous. Let  be given. Since
be given. Since  , there is constant
, there is constant  such that
such that  for all
for all  .
.
Let  be arbitrary. If
be arbitrary. If  , then we have
, then we have

From the uniform continuity of the function  on
on  and the function
and the function  in
in  , we get
, we get  as
as  .
.
If  , then we have
, then we have

as  .
.
Similarly, if  with
with  , then we have
, then we have

Note that if  , then
, then  and
and  . Therefore from the above obtained estimates, it follows that:
. Therefore from the above obtained estimates, it follows that:

As a result,  as
as  . Hence
. Hence  is an equicontinuous sequence of functions in
is an equicontinuous sequence of functions in  . Now an application of the Arzelá-Ascoli theorem yields that
. Now an application of the Arzelá-Ascoli theorem yields that  has a uniformly convergent subsequence on the compact subset
has a uniformly convergent subsequence on the compact subset  of
of  . Without loss of generality, call the subsequence of the sequence itself.
. Without loss of generality, call the subsequence of the sequence itself.
We show that  is Cauchy sequence in
is Cauchy sequence in  . Now
. Now  as
as  for all
for all  . Then for given
. Then for given  there exists an
there exists an  such that for
such that for  , then we have
, then we have

This shows that  is Cauchy. Since
is Cauchy. Since  is complete, then
is complete, then  converges to a point in
converges to a point in  . As
. As  is closed,
is closed,  converges to a point in
converges to a point in  . Hence,
. Hence,  is relatively compact and consequently
is relatively compact and consequently  is a continuous and compact operator on
is a continuous and compact operator on  .
.
Next, we show that  for all
for all  . Let
. Let  be arbitrary, then
be arbitrary, then

for all  . Taking the supremum over
. Taking the supremum over  , we obtain
, we obtain  for all
for all  . Hence hypothesis
. Hence hypothesis  of Theorem 2.4 holds.
of Theorem 2.4 holds.
Also we have

and therefore  . Now we apply Theorem 2.4 to conclude that (1.1) has a solution on
. Now we apply Theorem 2.4 to conclude that (1.1) has a solution on 
Finally, we show the local attractivity of the solutions for (1.1). Let  and
and  be any two solutions of (1.1) in
be any two solutions of (1.1) in  defined on
defined on  , then we get
, then we get

for all  . Since
. Since  ,
,  and
and  , for
, for  , there are real numbers
, there are real numbers  ,
,  and
and  such that
such that  for
for  ,
,  for all
for all  and
and  for all
for all  . If we choose
. If we choose  , then from the above inequality it follows that
, then from the above inequality it follows that  for
for  , where
, where  . This completes the proof.
. This completes the proof.
4. An Example
In this section we provide an example illustrating the main existence result contained in Theorem 3.2.
Example 4.1.
Consider the following quadratic Volterra integral equation of fractional order:

where  .
.
Observe that the above equation is a special case of (1.1). Indeed, if we put  and
and

Then we can easily check that the assumptions of Theorem 3.2 are satisfied. In fact, we have that the function  is continuous and satisfies assumption
is continuous and satisfies assumption  , where
, where  and
and  as in assumption
as in assumption  . We have that the function
. We have that the function  is continuous and it is easily seen that
is continuous and it is easily seen that  as
as  , thus assumption
, thus assumption  is satisfied. Next, let us notice that the function
is satisfied. Next, let us notice that the function  satisfies assumption
satisfies assumption  , where
, where  ,
,  and
and  . Thus
. Thus  . To check that assumption
. To check that assumption  is satisfied let us observe that the functions
is satisfied let us observe that the functions  appearing in that assumption take the form:
appearing in that assumption take the form:

Thus it is easily seen that  as
as  . Finally, let us note that in Remark 3.1 there are two constants
. Finally, let us note that in Remark 3.1 there are two constants  such that
such that  . It is also easy to check that
. It is also easy to check that  ,
,  and
and  . Then
. Then  . Hence, taking into account that
. Hence, taking into account that  (cf. [4]), all the assumptions of Theorem 3.2 are satisfied and (4.1) has a solution in the space
(cf. [4]), all the assumptions of Theorem 3.2 are satisfied and (4.1) has a solution in the space  . Moreover, solutions of (4.1) are uniformly locally attractive in the sense of Definition 2.1.
. Moreover, solutions of (4.1) are uniformly locally attractive in the sense of Definition 2.1.
References
Babakhani A, Daftardar-Gejji V: Existence of positive solutions of nonlinear fractional differential equations. Journal of Mathematical Analysis and Applications 2003,278(2):434-442. 10.1016/S0022-247X(02)00716-3
El Borai MM, El-Sayed WG, Abbas MI: Monotonic solutions of a class of quadratic singular integral equations of Volterra type. International Journal of Contemporary Mathematical Sciences 2007,2(1–4):89-102.
El Borai MM, Abbas MI: Solvability of an infinite system of singular integral equations. Serdica Mathematical Journal 2007,33(2-3):241-252.
El Borai MM, Abbas MI: On some integro-differential equations of fractional orders involving Carathéodory nonlinearities. International Journal of Modern Mathematics 2007,2(1):41-52.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Yverdon, Switzerland; 1993:xxxvi+976.
Srivastava HM, Saxena RK: Operators of fractional integration and their applications. Applied Mathematics and Computation 2001,118(1):1-52. 10.1016/S0096-3003(99)00208-8
Hu X, Yan J: The global attractivity and asymptotic stability of solution of a nonlinear integral equation. Journal of Mathematical Analysis and Applications 2006,321(1):147-156. 10.1016/j.jmaa.2005.08.010
Banaś J, O'Regan D: On existence and local attractivity of solutions of a quadratic Volterra integral equation of fractional order. Journal of Mathematical Analysis and Applications 2008,345(1):573-582. 10.1016/j.jmaa.2008.04.050
Rzepka B: On attractivity and asymptotic stability of solutions of a quadratic Volterra integral equation of fractional order. Topological Methods in Nonlinear Analysis 2008,32(1):89-102.
Kilbas AA, Trujillo JJ: Differential equations of fractional order: methods, results and problems. I. Applicable Analysis 2001,78(1-2):153-192. 10.1080/00036810108840931
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Podlubny I: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Dugundji J, Granas A: Fixed Point Theory. I, Monografie Matematyczne. Volume 61. Państwowe Wydawnictwo Naukowe, Warsaw, Poland; 1982:209.
Dhage BC: Nonlinear functional boundary value problems in Banach algebras involving Carathéodories. Kyungpook Mathematical Journal 2006,46(4):527-541.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abbas, M. On the Existence of Locally Attractive Solutions of a Nonlinear Quadratic Volterra Integral Equation of Fractional Order. Adv Differ Equ 2010, 127093 (2010). https://doi.org/10.1155/2010/127093
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/127093
 is Lipschitz with the Lipschitz constant
is Lipschitz with the Lipschitz constant  ,
, is completely continuous,
is completely continuous,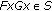 for all
for all  , and
, and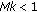 where
where  .
.