- Research Article
- Open access
- Published:
A Mixed Problem for Quasilinear Impulsive Hyperbolic Equations with Non Stationary Boundary and Transmission Conditions
Advances in Difference Equations volume 2010, Article number: 101959 (2010)
Abstract
The initial-boundary value problem for a class of linear and nonlinear equations in Hilbert space is considers. We prove the existence and uniqueness of solution of this problem. The results of this investigation are applied to solvability of initial-boundary value problems for quasilinear impulsive hyperbolic equations with non-stationary transmission and boundary conditions.
1. Abstract Model Initial Boundary Value Problem with Non Stationary Boundary and Transmission Conditions for the Impulsive Linear Hyperbolic Equations
In paper [1] there is given an abstract scheme of investigation of mixed problems for hyperbolic equations with non stationary boundary conditions. In this direction, some results were obtained in [2].
In this paper, we offer the analogues abstract model of investigation of mixed problem with non stationary boundary and transmission conditions for impulsive linear and semilinear hyperbolic equations.
1.1. Statement of the Problem and Main Theorem
Let  (
( ;
;  ;
;  ;
;  ) be Hilbert Spaces. Consider the following abstract initial-boundary value problem:
) be Hilbert Spaces. Consider the following abstract initial-boundary value problem:


where  ,
,  ,
,  ,
,  are the linear closed operators in
are the linear closed operators in  ;
;  are the linear operators from
are the linear operators from  to
to  ;
;  are the linear operators from
are the linear operators from  to
to  ;
;  are the linear operators from
are the linear operators from  to
to ;
;  ,
,  ,
,  ,
,  .
.
We will investigate this problem under the following conditions.
-
(i)
Let
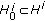 , and let
, and let 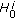 be densely in
be densely in  and continuously imbedded into it,
and continuously imbedded into it, 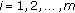 .
.
In the Hilbert space  , it was defined the system of the inner products
, it was defined the system of the inner products  , which generate uniform equivalent norms, that is,
, which generate uniform equivalent norms, that is,

For each  , the function
, the function  is continuously differentiable,
is continuously differentiable,  .
.
In the Hilbert space  , it was defined the system of the inner products
, it was defined the system of the inner products  , which generate uniform equivalent norms, that is,
, which generate uniform equivalent norms, that is,

For each  , the function
, the function  is continuously differentiable.
is continuously differentiable.
-
(ii)
For each
 and
and 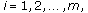
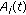 is a linear closed operator in
is a linear closed operator in  whose domain is
whose domain is  ;
;  acts boundedly from
acts boundedly from 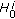 to
to 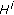 ;
; 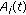 is strongly continuously differentiable.
is strongly continuously differentiable. -
(iii)
The linear operators
 , that act from
, that act from 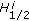 to
to 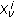 , bounded, where
, bounded, where  is interpolation space between
is interpolation space between 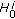 and
and 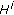 of order
of order  (see [3]).
(see [3]). -
(iv)
For each
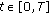 , the linear operators
, the linear operators 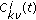 , that act from
, that act from 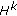 to
to  , are bounded;
, are bounded;  is strongly continuously differentiable
is strongly continuously differentiable  ,
, 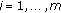 ;
; 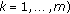 .
. -
(v)
The linear operators
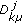 , from
, from 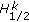 into
into 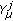 , act boundedly
, act boundedly 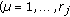 ,
,  ;
; 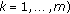 .
.
Let us introduce the following designations:

From condition (v), it follows that the space  with the norm
with the norm

is a subspace of

-
(vi)
Let the linear manifold
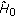 be dense in
be dense in 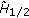 , and let linear manifold
, and let linear manifold  be dense in
be dense in  .
. -
(vii)
(Green's Identity). For arbitrary
 and
and  , the following identity is valid:
, the following identity is valid:

-
(viii)
For all
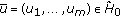 , the following inequality is fulfilled:
, the following inequality is fulfilled: 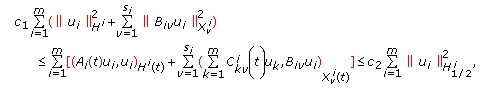 (1.9)
(1.9)
where  .
.
-
(ix)
For each
 , an operator pencil
, an operator pencil
 (1.10)
(1.10)
which acts boundedly from  to
to  , has a regular point
, has a regular point  , where
, where

-
(x)
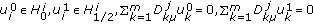
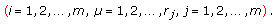 (1.12)
(1.12)
-
(xi)
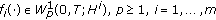 ,
,

Definition 1.1.
The function  is called a solution of problem (1.1)-(1.2) if the function
is called a solution of problem (1.1)-(1.2) if the function  from
from  to
to  is continuous, and the function
is continuous, and the function

from  to
to  is twice continuously differentiable and (1.1)-(1.2) are satisfied.
is twice continuously differentiable and (1.1)-(1.2) are satisfied.
Theorem 1.2.
Let conditions (i)–(xi) are satisfied, then the problem (1.1)-(1.2) has a unique solution.
Proof.
We define the operator  in the Hilbert space
in the Hilbert space  in the following way:
in the following way:

Then the problem (1.1)-(1.2) is represented as the Cauchy problem

where  ,
,

It is obvious that if  is the solution of problem (1.1)-(1.2), then
is the solution of problem (1.1)-(1.2), then  is the solution of the problem (1.16). On the contrary, if
is the solution of the problem (1.16). On the contrary, if

is the solution of problem (1.16), then  ,
, and
and  is the solution of problem (1.1)-(1.2).
is the solution of problem (1.1)-(1.2).
Let us define the system of inner product in Hilbert space  in the following way:
in the following way:

where  ,
, .
.
We denote space  with inner product (1.19) by
with inner product (1.19) by  .
.
We will prove later the following auxiliary results.
Statement 1.3.
There exists such  , that
, that

and the function  is continuously differentiable, where
is continuously differentiable, where  =
=  .
.
Statement 1.4.
 is a symmetric operator in
is a symmetric operator in  for each
for each  .
.
Statement 1.5.
 has a regular point for each
has a regular point for each  in
in  .
.
 is symmetric and
is symmetric and  , for some
, for some  ; therefore, for each
; therefore, for each  is a selfadjoint operator in
is a selfadjoint operator in  (see [4, chapter x]).
(see [4, chapter x]).
Taking into account (viii) and Statement 1.3, we get

that is,  is a lower semibounded selfadjoint operator in
is a lower semibounded selfadjoint operator in  .
.
Thus, the operator  is selfadjoint and positive definite, where
is selfadjoint and positive definite, where  .
.
Problem (1.16) can be rewritten as

It is known that if  and
and  , then the problem (1.22) has a unique solution
, then the problem (1.22) has a unique solution 



 (see [5, 6]).
(see [5, 6]).
To complete the proof of the theorem, we need to show that  and
and  .
.
By conditions of the theorem 
 ;
;  ,
,  and
and  are bounded operators from
are bounded operators from  to
to  . Therefore,
. Therefore,

On the other hand,  and
and 
 , therefore,
, therefore, 
 . Consequently,
. Consequently,

From the definition of interpolation spaces (see [3, chapter 1], [7, chapter 1]), we get the following inclusion:

By virtue of definition, the powers of positive selfadjoint operator (see [8, chapter 2], [7, chapter 1]), we have that  and
and

Assume that  , then
, then

By virtue of conditions (ii), (viii), (1.26), and (1.27), we get

Let  . By virtue of condition (vi),
. By virtue of condition (vi),  is dense in
is dense in  ; therefore, there exists a sequence
; therefore, there exists a sequence  , such that
, such that  and
and

Hence it follows, that

Then from (1.28) and (1.30) it follows that  is fundamental in
is fundamental in  , that is,
, that is,

where  ,….
,….
Thus, there exists  such that
such that

On the other hand,  , therefore,
, therefore,

Hence,

where  . From this, by virtue of (1.29),
. From this, by virtue of (1.29),  , that is,
, that is,

Thus,  . The theorem is proved.
. The theorem is proved.
1.2. Proof of Auxiliary Results
Validity of Statement 1.3 follows from condition (i), the Statement 1.4 from condition (vii).
Proof.
Consider in Hilbert space  the equation
the equation

where  .
.
Equation (1.36) is equivalent to the following system of differential-operator equations:

By virtue of (ix), problem (1.37) has a solution  for some
for some  . Thus, for each
. Thus, for each  ,
,

where  is an identity operator in
is an identity operator in  , that is,
, that is,  has a regular point.
has a regular point.
2. Abstract Model of Initial Boundary Value Problem with Non Stationary Boundary and Transmission Conditions for the Impulsive Semilinear Hyperbolic Equations
Consider the following initial boundary value problem:

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  satisfy all conditions of Theorem 1.2.
satisfy all conditions of Theorem 1.2.
Assume, that the nonlinear operators  and
and  satisfy the following conditions.
satisfy the following conditions.
(xi′)Suppose that the nonlinear operators

satisfy the local Lipschitz conditions in the following sense: for arbitrary  ,
,

where  ,
,

Theorem 2.1.
Let conditions (i)–(x) and (xi′) be satisfied, then there exists  , such that the problem (2.1) has a unique solution
, such that the problem (2.1) has a unique solution

Additionally, if

where  , then
, then  . Otherwise, there exists
. Otherwise, there exists  , such that
, such that

In the Hilbert space  , the problem (2.1) is represented as the Cauchy problem
, the problem (2.1) is represented as the Cauchy problem

where  ,
,

From ( ), it follows that, for arbitrary
), it follows that, for arbitrary  ,
,

where  .
.
Thus, the nonlinear operator  satisfies the condition of local solvability of the Cauchy problem for the quasilinear hyperbolic equations in Hilbert space (see [6, 9]). Taking this into account, the problem (2.8) has a unique solution
satisfies the condition of local solvability of the Cauchy problem for the quasilinear hyperbolic equations in Hilbert space (see [6, 9]). Taking this into account, the problem (2.8) has a unique solution

3. Initial Boundary Value Problem with Non Stationary Boundary and Transmission Condition for the Impulsive Semilinear Hyperbolic Equations
Let  . We consider in the domain
. We consider in the domain  the following mixed problem
the following mixed problem

where  ,
,  ,
,  ,
,  are some functions,
are some functions,  and
and  are some functionals, which will be specified below,
are some functionals, which will be specified below,  .
.
Recently, differential equations with impulses are great interest because of the needs of modern technology, where impulsive automatic control systems and impulsive computing systems are very important and intensively develop broadening the scope of their applications in technical problems, heterogeneous by their physical nature and functional purpose (see [10,chapter 1]).
Assume that the following conditions are held:
-
(10)
 ;
; 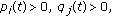
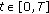 ,
,  ,
, -
(20)
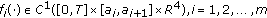 ,
, -
(30)
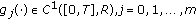 ,
, -
(40)
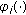 are nonlinear functionals acting from
are nonlinear functionals acting from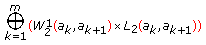 (3.2)
(3.2)to
 and for arbitrary
and for arbitrary  the following inequality holds
the following inequality holds (3.3)
(3.3)where
 ,
,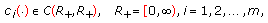 (3.4)
(3.4) -
(50)
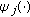 are nonlinear functionals acting from
are nonlinear functionals acting from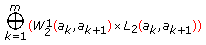 (3.5)
(3.5)to
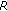 and for arbitrary
and for arbitrary 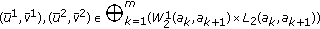 the following inequality holds
the following inequality holds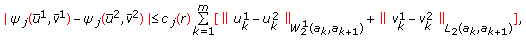 (3.6)
(3.6)where
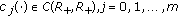 , and
, and  —is defined as in (3.3),
—is defined as in (3.3), -
(60)
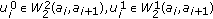 ,
, 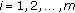 , where
, where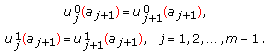 (3.7)
(3.7)By applying Theorem 2.1, we obtain the following result.
Theorem 3.1.
Let conditions (10)–(60) be held, then there exists a  , such that the problem (3.1) has a unique solution
, such that the problem (3.1) has a unique solution  , where
, where

Proof.
Let us denote  ,
,  ,
,  ,
, ,
,  ,
, ,
, ,
,  , where
, where  ,
, .
.
In space  and
and  are defined the following inner products:
are defined the following inner products:

From differentiability of the functions  ,
,  , and
, and  ,
, it follows that the condition (i) is satisfied.
it follows that the condition (i) is satisfied.
Let us define the following operators:
 ,
,
 ,
,
 ,
,
 , for all other
, for all other  ,
,
 ,
,
 ,
,
 , for all other
, for all other  ,
,
 ,
,
 .
.
We also define the nonlinear operators as follows:
 ,
,
 ,
,
 ,
,
 .
.
It is easy to verify that linear operators  and the nonlinear operators
and the nonlinear operators  ,
,  satisfy the conditions of Theorem 2.1, and the problem (3.1) is represented as an abstract initial boundary-value problem in the following way:
satisfy the conditions of Theorem 2.1, and the problem (3.1) is represented as an abstract initial boundary-value problem in the following way:

We will show that conditions of Theorem 2.1 are satisfied. Conditions (i)–(v) follow immediately from definitions of spaces  and operators
and operators  , and traces theorems (see [3, chapter 2]), where
, and traces theorems (see [3, chapter 2]), where  ;
;  ;
;  ;
;  ;
;  .
.
The linear manifolds  and
and  are defined in the following way:
are defined in the following way:

We also define the spaces

Statement 3.2.
 is dense in
is dense in

Proof.
Assume that  . Consider the following functions:
. Consider the following functions:

From definitions of  ,
,  , we can see that
, we can see that

Let  . Consider the function
. Consider the function

It is obvious that  . On the other hand,
. On the other hand,  , where
, where 
 is a space of infinitely differentiable finite functions. Therefore, for an arbitrary
is a space of infinitely differentiable finite functions. Therefore, for an arbitrary  , there exist the functions
, there exist the functions  ,
,  , such that
, such that

By denoting  from (3.17), we get
from (3.17), we get

where  .
.
Thus,

The following statement is proved in the same way.
Statement 3.3.
 is dense
is dense  .
.
Now, we prove that the condition (vi) holds.
Let  , then
, then

Similary, we obtain the following identity:

Thus, by virtue of (3.20)-(3.21), the condition (vi) holds.
From (3.20) or (3.21), putting  , we also obtain the identity
, we also obtain the identity

that is, condition (viii) is satisfied,  .
.
Now, we verify fulfillment of condition (ix). To that end, we consider the mixed problem


where  ,
, ;
;  ,
,  ,
,  .
.
Let  be the extend of function
be the extend of function  to
to  . We consider the system of the differential equations
. We consider the system of the differential equations

Hence, we have

where  is a Fourier transformation of the function
is a Fourier transformation of the function  . From (3.26), we obtain
. From (3.26), we obtain  , then functions
, then functions  satisfy (3.25), and their constrictions on (
satisfy (3.25), and their constrictions on ( ) satisfy the (3.23). It is clear that
) satisfy the (3.23). It is clear that  . Considering linearity of the problem (3.23), (3.24), the solution can be represented in the form
. Considering linearity of the problem (3.23), (3.24), the solution can be represented in the form

where  is a solution of the following problem:
is a solution of the following problem:


where  ,
,

A general solution of a system (3.28) is found in the following form:

Then, for determination of  , from (3.29), we get the following system of the algebraic equations:
, from (3.29), we get the following system of the algebraic equations:

Let  be a matrix of coefficients of system (3.32). From (3.32), it is clear that
be a matrix of coefficients of system (3.32). From (3.32), it is clear that  , where
, where  and
and  as
as  . Thus, for sufficiently large
. Thus, for sufficiently large  ,
,  is invertible and
is invertible and  . Therefore, the system (3.32) has a unique solution.
. Therefore, the system (3.32) has a unique solution.
Thus, for sufficiently positive large  , the problem (3.23)-(3.24) has a unique solution
, the problem (3.23)-(3.24) has a unique solution  .
.
Thus, the condition (ix) is satisfied. The fulfillment of other conditions follows from  .
.
Now, let us consider a class of nonlinear equations, for which the large solvability theorem takes place.
Let

where  ,
,  ,
,  ;
;  and
and
 and
and  ,
,  satisfy the conditions
satisfy the conditions  –
– .
.
 ,
,
 ,
,
 ,
,
where  ,
,  ,
,  .
.
Theorem 3.4.
Let conditions  be held and initial data satisfy the condition
be held and initial data satisfy the condition  , then the problem (3.1) has a unique solution
, then the problem (3.1) has a unique solution  , where
, where

References
Yakubov Y: Hyperbolic differential-operator equations on a whole axis. Abstract and Applied Analysis 2004, (2):99-113. 10.1155/S1085337504311103
Lancaster P, Shkalikov A, Ye Q: Strongly definitizable linear pencils in Hilbert space. Integral Equations and Operator Theory 1993,17(3):338-360. 10.1007/BF01200290
Lions J-L, Magenes E: Problemes aux Limites non Homogenes et Applications. Volume 1. Dunod, Paris, France; 1968.
Reed M, Simon B: Methods of Modern Mathematical Physics. II. Fourier Analysis, Self-Adjointness. Academic Press, New York, NY, USA; 1975:xv+361.
Kato T: Linear evolution equations of "hyperbolic" type. II. Journal of the Mathematical Society of Japan 1973, 25: 648-666. 10.2969/jmsj/02540648
Hughes TJR, Kato T, Marsden JE: Well-posed quasi-linear second-order hyperbolic systems with applications to nonlinear elastodynamics and general relativity. Archive for Rational Mechanics and Analysis 1977,63(3):273-294. 10.1007/BF00251584
Yakubov S, Yakubov Y: Differential-Operator Equations. Ordinary and Partial Differential Equations, Chapman & Hall/CRC Monographs and Surveys in Pure and Applied Mathematics. Volume 103. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2000:xxvi+541.
Krein SQ: Linear Differential Equation in Banach Spaces. Nauka, Moscow, Russia; 1967.
Aliev AB: Solvability "in the large" of the Cauchy problem for quasilinear equations of hyperbolic type. Doklady Akademii Nauk SSSR 1978,240(2):249-252.
Samoĭlenko AM, Perestyuk NA: Impulsive Differential Equations, World Scientific Series on Nonlinear Science. Series A: Monographs and Treatises. Volume 14. World Scientific, River Edge, NJ, USA; 1995:x+462.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aliev, A.B., Mamedova, U.M. A Mixed Problem for Quasilinear Impulsive Hyperbolic Equations with Non Stationary Boundary and Transmission Conditions. Adv Differ Equ 2010, 101959 (2010). https://doi.org/10.1155/2010/101959
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/101959
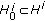 , and let
, and let 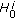 be densely in
be densely in  and continuously imbedded into it,
and continuously imbedded into it, 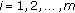 .
. and
and 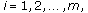
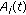 is a linear closed operator in
is a linear closed operator in  whose domain is
whose domain is  ;
;  acts boundedly from
acts boundedly from 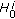 to
to 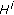 ;
; 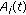 is strongly continuously differentiable.
is strongly continuously differentiable. , that act from
, that act from 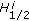 to
to 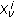 , bounded, where
, bounded, where  is interpolation space between
is interpolation space between 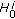 and
and 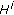 of order
of order  (see [
(see [ , the linear operators
, the linear operators 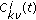 , that act from
, that act from 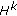 to
to  , are bounded;
, are bounded;  is strongly continuously differentiable
is strongly continuously differentiable  ,
, 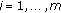 ;
; 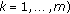 .
.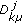 , from
, from 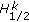 into
into 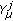 , act boundedly
, act boundedly 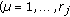 ,
,  ;
; 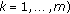 .
.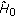 be dense in
be dense in 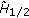 , and let linear manifold
, and let linear manifold  be dense in
be dense in  .
. and
and  , the following identity is valid:
, the following identity is valid: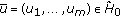 , the following inequality is fulfilled:
, the following inequality is fulfilled: 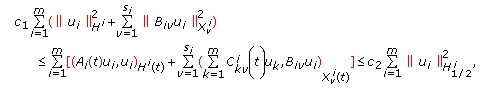
 , an operator pencil
, an operator pencil

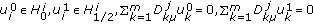
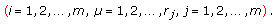
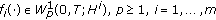 ,
, ;
; 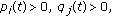
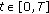 ,
,  ,
,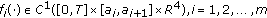 ,
,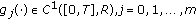 ,
,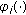 are nonlinear functionals acting from
are nonlinear functionals acting from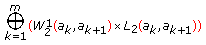
 and for arbitrary
and for arbitrary  the following inequality holds
the following inequality holds
 ,
,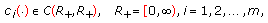
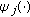 are nonlinear functionals acting from
are nonlinear functionals acting from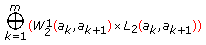
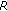 and for arbitrary
and for arbitrary 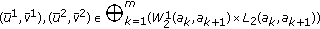 the following inequality holds
the following inequality holds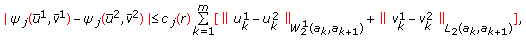
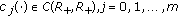 , and
, and  —is defined as in (3.3),
—is defined as in (3.3),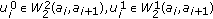 ,
, 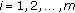 , where
, where