- Research Article
- Open access
- Published:
Meromorphic Solutions of Some Complex Difference Equations
Advances in Difference Equations volume 2009, Article number: 982681 (2009)
Abstract
The main purpose of this paper is to present the properties of the meromorphic solutions of complex difference equations of the form  , where
, where  is a collection of all subsets of
is a collection of all subsets of  ,
,  are distinct, nonzero complex numbers,
are distinct, nonzero complex numbers,  is a transcendental meromorphic function,
is a transcendental meromorphic function,  's are small functions relative to
's are small functions relative to  , and
, and  is a rational function in
is a rational function in  with coefficients which are small functions relative to
with coefficients which are small functions relative to  .
.
1. Introduction
We assume that the readers are familiar with the basic notations of Nevanlinna's value distribution theory; see [1–3].
Recent interest in the problem of integrability of difference equations is a consequence of the enormous activity on Painlevé differential equations and their discrete counterparts during the last decades. Many people study this topic and obtain some results; see [4–15]. In [4], Ablowitz et al. obtained a typical result as follows.
Theorem 1 A.
If a complex difference equation

with rational coefficients  and
and  admits a transcendental meromorphic solution of finite order, then
admits a transcendental meromorphic solution of finite order, then 
In [10], Heittokangas et al. extended and improved the above result to higher-order difference equations of more general type. However, by inspecting the proofs in [4], we can find a more general class of complex difference equations by making use of a similar technique; see [10, 15].
In this paper, we mention the above details, used in [4, 10, 15], with equations of the form

where  is a collection of all subsets of
is a collection of all subsets of  ,
,  are distinct, nonzero complex numbers,
are distinct, nonzero complex numbers,  is a transcendental meromorphic function,
is a transcendental meromorphic function,  's are small functions relative to
's are small functions relative to  and
and  is a rational function in
is a rational function in  with coefficients which are small functions relative to
with coefficients which are small functions relative to  .
.
2. Main Results
In [10], Heittokangas et al. considered the complex difference equations of the form

with rational coefficients  and
and  . They obtained the following theorem.
. They obtained the following theorem.
Theorem 2 B.
Let  . If the difference equation (2.1) with rational coefficients
. If the difference equation (2.1) with rational coefficients  and
and  admits a transcendental meromorphic solution of finite order
admits a transcendental meromorphic solution of finite order  , then
, then  , where
, where  .
.
It is obvious that the left-hand side of (2.1) is just a product only. If we consider the left-hand side of (2.1) is a product sum, we also have the following theorem.
Theorem 2.1.
Suppose that  are distinct, nonzero complex numbers and that
are distinct, nonzero complex numbers and that  is a transcendental meromorphic solution of
is a transcendental meromorphic solution of

with coefficients  's,
's,  and
and  are small functions relative to
are small functions relative to  . If the order
. If the order  is finite, then
is finite, then  , where
, where  .
.
It seems that the equivalent proposition is a known fact. In [15], Laine et al. obtain the similar result to the following Corollary 2.2. Here, for the convenience for the readers, we list it, that is, we have the following corollary.
Corollary 2.2.
Suppose that  are distinct, nonzero complex numbers and that
are distinct, nonzero complex numbers and that  is a transcendental meromorphic solution of (2.2) with rational coefficients
is a transcendental meromorphic solution of (2.2) with rational coefficients  's,
's,  and
and  . If
. If  , then the order
, then the order  is infinite.
is infinite.
In [15], when the left-hand side of (2.1) is just a sum, Laine et al. obtained the following theorem.
Theorem 2 C.
Suppose that  are distinct, nonzero complex numbers and that
are distinct, nonzero complex numbers and that  is a transcendental meromorphic solution of
is a transcendental meromorphic solution of

where the coefficients  's are nonvanishing small functions relative to
's are nonvanishing small functions relative to  and where
and where  and
and  are relatively prime polynomials in
are relatively prime polynomials in  over the field of small functions relative to
over the field of small functions relative to  . Moreover, one assumes that
. Moreover, one assumes that  ,
,

and that, without restricting generality,  is a monic polynomial. If there exists
is a monic polynomial. If there exists  such that for all
such that for all  sufficiently large,
sufficiently large,

where  then either the order
then either the order  , or
, or

where  is a small meromorphic function relatively to
is a small meromorphic function relatively to  .
.
They obtained Theorem C and presented a problem that whether the result will be correct if we replace the left-hand side of (2.3) by a product sum as in Theorem 2.1. Here, under the new hypothesis, we consider the left-hand side of (2.3) is a product sum and obtain what follows.
Theorem 2.3.
Suppose that  are distinct, nonzero complex numbers and that
are distinct, nonzero complex numbers and that  is a transcendent meromorphic solution of
is a transcendent meromorphic solution of

where the coefficients  's are nonvanishing small functions relative to
's are nonvanishing small functions relative to  and where
and where  are relatively prime polynomials in
are relatively prime polynomials in  over the field of small functions relative to
over the field of small functions relative to  . Moreover, one assumes that
. Moreover, one assumes that  ,
,

and that, without restricting generality,  is a monic polynomial. If there exists
is a monic polynomial. If there exists  such that for all
such that for all  sufficiently large,
sufficiently large,

where  . Then either the order
. Then either the order  or
or

where  is a small meromorphic function relative to
is a small meromorphic function relative to  .
.
3. The Proofs of Theorems
Let  be a meromorphic function. Then for all irreducible rational functions in
be a meromorphic function. Then for all irreducible rational functions in  ,
,

with meromorphic coefficients  and
and  , the characteristic function of
, the characteristic function of  satisfies
satisfies

where  and
and

In the particular case when

we have

Lemma 3.2.
Given distinct complex numbers  a meromorphic function
a meromorphic function  and meromorphic functions
and meromorphic functions  's, one has
's, one has

where  . In the particular case when
. In the particular case when

one has

Remark 3.3.
Observe that the term  does not appear in (3.6). This follows by a careful inspection of the proof of [16, Proposition B.15, Theorem B.16].
does not appear in (3.6). This follows by a careful inspection of the proof of [16, Proposition B.15, Theorem B.16].
Remark 3.4.
Note that the inequality (3.6) remains true, if we replace the characteristic function  by the proximity function
by the proximity function  (or by the counting function
(or by the counting function  ).
).
Lemma 3.5 (see [12, Theorem 2.1]).
Let  be a nonconstant meromorphic function of finite order,
be a nonconstant meromorphic function of finite order,  and
and  . Then
. Then

for all  outside of a possible exceptional set
outside of a possible exceptional set  with finite logarithmic measure
with finite logarithmic measure 
Lemma 3.6 (see [12, Lemma 2.2]).
Let  be a nondecreasing continuous function,
be a nondecreasing continuous function,  and let
and let  be the set of all
be the set of all  such that
such that

If the logarithmic measure of  is infinite, that is,
is infinite, that is,  then
then

Proof of Theorem 2.1.
Since the coefficients  's,
's,  and
and  in (2.2) are small functions relative to
in (2.2) are small functions relative to  , that is,
, that is,

hold for all  outside of a possible exceptional set
outside of a possible exceptional set  with finite logarithmic measure
with finite logarithmic measure 
Let  be a finite order meromorphic solution of (2.2). According to Lemma 3.5, we have, for any
be a finite order meromorphic solution of (2.2). According to Lemma 3.5, we have, for any  ,
,

where the exceptional set  associated to
associated to  is of finite logarithmic measure
is of finite logarithmic measure 
It follows from Lemma 3.6 that

for any  .
.
Now, equating the Nevanlinna characteristic function on both sides of (2.2), and applying Lemmas 3.1 and 3.2, we have

where  .
.
Therefore, by (3.13) and (3.14), it follows that

for all  outside of a possible exceptional set
outside of a possible exceptional set  with finite logarithmic measure. Dividing this by
with finite logarithmic measure. Dividing this by  and letting
and letting  outside of the exceptional set
outside of the exceptional set  and
and  of
of  and
and  , respectively, we have
, respectively, we have  The proof of Theorem 2.1 is completed.
The proof of Theorem 2.1 is completed.
Example 3.7.
Let  be a constant such that
be a constant such that  where
where  , and let
, and let  . We see that
. We see that  solves
solves

This shows that the equality  is arrived in Theorem 2.1 if
is arrived in Theorem 2.1 if 
Example 3.8.
Let  . We see that
. We see that  solves
solves

This shows that the case  may occur in Theorem 2.1 if
may occur in Theorem 2.1 if 
Lemma 3.9 (see [17]).
Let  be a meromorphic function and let
be a meromorphic function and let  be given by
be given by

Then either

or

Lemma 3.10 (see [15]).
Let  be a nonconstant meromorphic function and let
be a nonconstant meromorphic function and let  ,
,  be two polynomials in
be two polynomials in  with meromorphic coefficients small functions relative to
with meromorphic coefficients small functions relative to  . If
. If  and
and  have no common factors of positive degree in
have no common factors of positive degree in  over the field of small functions relative to
over the field of small functions relative to  , then
, then

Proof of Theorem 2.3.
Suppose that the second alternative of the conclusion is not correct. Then we have, by using Lemmas 3.9, 3.10, 3.2, (2.7), and (2.9),

where 
Thus, we have

Now assuming that  , we have
, we have  and for all
and for all 

It follows from Lemmas 3.1, 3.2, (3.23), and (2.9) we have

From this, we have

Together with (3.25)–(3.27), we can use method of induction and obtain, for  ,
,

Moreover, we immediately obtain from (3.28) that

and for sufficiently large  , we have
, we have

It also follows from Lemma 3.6 that

for any  , assuming that
, assuming that  is of finite order.
is of finite order.
Now (3.31) combined with (3.29) and (3.30) yields an immediate contradiction if  . Therefore the only possibility is that
. Therefore the only possibility is that  is of infinite order. The proof of Theorem 2.3 is completed.
is of infinite order. The proof of Theorem 2.3 is completed.
References
Gao S-A, Chen Z-X, Chen T-W: Oscillation Theory of Linear Differential Equation. University of Science and Technology Press, Huazhong, China; 1998.
Hayman WK: Meromorphic Functions, Oxford Mathematical Monographs. Clarendon Press, Oxford, UK; 1964:xiv+191.
Laine I: Nevanlinna Theory and Complex Differential Equations, Studies in Mathematics. Volume 15. de Gruyter, Berlin, Germany; 1993:viii+341.
Ablowitz MJ, Halburd R, Herbst B: On the extension of the Painlevé property to difference equations. Nonlinearity 2000,13(3):889-905. 10.1088/0951-7715/13/3/321
Bergweiler W, Langley JK: Zeros of differences of meromorphic functions. Mathematical Proceedings of the Cambridge Philosophical Society 2007,142(1):133-147. 10.1017/S0305004106009777
Chen Z-X, Shon KH: On zeros and fixed points of differences of meromorphic functions. Journal of Mathematical Analysis and Applications 2008,344(1):373-383. 10.1016/j.jmaa.2008.02.048
Chen Z-X, Huang Z-B, Zheng X-M: A note "Value distribution of difference polynomials". to appear in Acta Mathematica Sinica
Chiang Y-M, Feng S-J:On the Nevanlinna characteristic of
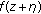 and difference equations in the complex plane. Ramanujan Journal 2008,16(1):105-129. 10.1007/s11139-007-9101-1
and difference equations in the complex plane. Ramanujan Journal 2008,16(1):105-129. 10.1007/s11139-007-9101-1Gundersen GG, Heittokangas J, Laine I, Rieppo J, Yang D: Meromorphic solutions of generalized Schröder. Aequationes Mathematicae 2002,63(1-2):110-135. 10.1007/s00010-002-8010-z
Heittokangas J, Korhonen R, Laine I, Rieppo J, Tohge K: Complex difference equations of Malmquist type. Computational Methods and Function Theory 2001,1(1):27-39.
Halburd RG, Korhonen RJ: Difference analogue of the lemma on the logarithmic derivative with applications to difference equations. Journal of Mathematical Analysis and Applications 2006,314(2):477-487. 10.1016/j.jmaa.2005.04.010
Halburd RG, Korhonen RJ: Nevanlinna theory for the difference operator. Annales Academiæ Scientiarium Fennicæ. Mathematica 2006,31(2):463-478.
Halburd RG, Korhonen RJ: Existence of finite-order meromorphic solutions as a detector of integrability in difference equations. Physica D 2006,218(2):191-203. 10.1016/j.physd.2006.05.005
Ishizaki K, Yanagihara N: Wiman-Valiron method for difference equations. Nagoya Mathematical Journal 2004, 175: 75-102.
Laine I, Rieppo J, Silvennoinen H: Remarks on complex difference equations. Computational Methods and Function Theory 2005,5(1):77-88.
Gromak V, Laine I, Shimomura S: Painlevé Differential Equations in the Complex Plane, Studies in Mathematics. Volume 28. de Gruyter, New York, NY, USA; 2002.
Weissenborn G: On the theorem of Tumura and Clunie. The Bulletin of the London Mathematical Society 1986,18(4):371-373. 10.1112/blms/18.4.371
Acknowledgments
The authors are very grateful to the referee for his (her) many valuable comments and suggestions which greatly improved the presentation of this paper. The project was supposed by the National Natural Science Foundation of China (no. 10871076), and also partly supposed by the School of Mathematical Sciences Foundation of SCNU, China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Huang, ZB., Chen, ZX. Meromorphic Solutions of Some Complex Difference Equations. Adv Differ Equ 2009, 982681 (2009). https://doi.org/10.1155/2009/982681
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/982681
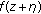 and difference equations in the complex plane. Ramanujan Journal 2008,16(1):105-129. 10.1007/s11139-007-9101-1
and difference equations in the complex plane. Ramanujan Journal 2008,16(1):105-129. 10.1007/s11139-007-9101-1