- Research Article
- Open access
- Published:
A Survey on Semilinear Differential Equations and Inclusions Involving Riemann-Liouville Fractional Derivative
Advances in Difference Equations volume 2009, Article number: 981728 (2009)
Abstract
We establish sufficient conditions for the existence of mild solutions for some densely defined semilinear functional differential equations and inclusions involving the Riemann-Liouville fractional derivative. Our approach is based on the  -semigroups theory combined with some suitable fixed point theorems.
-semigroups theory combined with some suitable fixed point theorems.
1. Introduction
Differential equations and inclusions of fractional order have recently proved to be valuable tools in the modeling of many phenomena in various fields of science and engineering. Indeed we can find numerous applications in viscoelasticity, electrochemistry, electromagnetism, and so forth. For details, including some applications and recent results, see the monographs of Kilbas et al. [1], Kiryakova [2], Miller and Ross [3], Podlubny [4] and Samko et al. [5], and the papers of Agarwal et al. [6], Diethelm et al. [7, 8], El-Sayed [9–11], Gaul et al. [12], Glockle and Nonnenmacher [13], Lakshmikantham and Devi [14], Mainardi [15], Metzler et al. [16], Momani et al. [17, 18], Podlubny et al. [19], Yu and Gao [20] and the references therein. Some classes of evolution equations have been considered by El-Borai [21, 22], Jaradat et al. [23] studied the existence and uniqueness of mild solutions for a class of initial value problem for a semilinear integrodifferential equation involving the Caputo's fractional derivative.
In this survey paper, we give existence results for various classes of initial value problems for fractional semilinear functional differential equations and inclusions, both cases of finite and infinite delay are considered. More precisely the paper is organized as follows. In the second section we introduce notations, definitions, and preliminary facts that will be used in the remainder of this paper. In the third section we will be concerned with semilinear functional differential equations with finite as well infinite delay. In the forth section, we consider semilinear functional differential equation of neutral type for the both cases of finite and infinite delay. Section 5 is devoted to the study of functional differential inclusions, we examine the case when the right-hand side is convex valued as well as nonconvex valued. In Section 6, we will be concerned with perturbed functional differential equations and inclusions. In the last section, we give some existence results of extremal solutions in ordered Banach spaces.
2. Preliminaries
In this section, we introduce notations, definitions, and preliminary facts which are used throughout this paper. Let  be a Banach space and
be a Banach space and  a compact real interval.
a compact real interval.  is the Banach space of all continuous functions from
is the Banach space of all continuous functions from  into
into  with the norm
with the norm

For  the norm of
the norm of  is defined by
is defined by

For  the norm of
the norm of  is defined by
is defined by

 denotes the Banach space of bounded linear operators from
denotes the Banach space of bounded linear operators from  into
into  with norm
with norm

 denotes the Banach space of measurable functions
denotes the Banach space of measurable functions  which are Bochner integrable normed by
which are Bochner integrable normed by

Definition 2.1.
A semigroup of class  is a one parameter family
is a one parameter family  satisfying the conditions
satisfying the conditions
-
(i)

-
(ii)
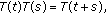 for all
for all 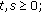
-
(iii)
the map
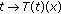 is strongly continuous, for each
is strongly continuous, for each 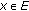 , that is,
, that is,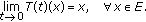 (2.6)
(2.6)
It is well known that the operator  generates a
generates a  semigroup if
semigroup if  satisfies
satisfies
-
(i)
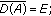
-
(ii)
the Hille-Yosida condition, that is, there exists
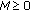 and
and  such that
such that 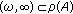 ,
, 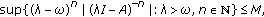 where
where 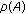 is the resolvent set of
is the resolvent set of 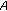 and
and 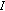 is the identity operator in
is the identity operator in  .
.
For more details on strongly continuous operators, we refer the reader to the books of Goldstein [24], Fattorini [25], and the papers of Travis and Webb [26, 27], and for properties on semigroup theory we refer the interested reader to the books of Ahmed [28], Goldstein [24], and Pazy [29].
In all our paper we adopt the following definitions of fractional primitive and fractional derivative.
The Riemann-Liouville fractional primitive of order  of a function
of a function  of order
of order  is defined by
is defined by

provided the right side is pointwise defined on  , and where
, and where  is the gamma function.
is the gamma function.
For instance,  exists for all
exists for all  , when
, when  ; note also that when
; note also that when  , then
, then  and moreover
and moreover 
The Riemann-Liouville fractional derivative of order  of a continuous function
of a continuous function  is defined by
is defined by

Let  be a metric space. We use the notations
be a metric space. We use the notations

Consider  given by
given by

where  Then
Then  is a metric space and
is a metric space and  is a generalized metric space (see [30]).
is a generalized metric space (see [30]).
A multivalued map  is said to be measurable if, for each
is said to be measurable if, for each  , the function
, the function  defined by
defined by

is measurable.
Definition 2.4.
A measurable multivalued function  is said to be integrably bounded if there exists a function
is said to be integrably bounded if there exists a function  such that
such that  a.e.
a.e.  for all
for all 
A multivalued map  is convex (closed) valued if
is convex (closed) valued if  is convex (closed) for all
is convex (closed) for all  .
.  is bounded on bounded sets if
is bounded on bounded sets if  is bounded in
is bounded in  for all
for all  , that is,
, that is,  .
.
 is called upper semicontinuous (u.s.c. for short) on
is called upper semicontinuous (u.s.c. for short) on  if for each
if for each  the set
the set  is nonempty, closed subset of
is nonempty, closed subset of  , and for each open set
, and for each open set  of
of  containing
containing  , there exists an open neighborhood
, there exists an open neighborhood  of
of  such that
such that  is said to be completely continuous if
is said to be completely continuous if  is relatively compact for every
is relatively compact for every  If the multivalued map
If the multivalued map  is completely continuous with nonempty compact valued, then
is completely continuous with nonempty compact valued, then  is u.s.c. if and only if
is u.s.c. if and only if  has closed graph, that is,
has closed graph, that is,  imply
imply 
Definition 2.5.
A multivalued map  is said to be Carathéodory if
is said to be Carathéodory if
-
(i)
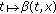 is measurable for each
is measurable for each 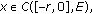
-
(ii)
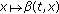 is u.s.c. for almost all
is u.s.c. for almost all 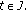
Furthermore, a Carathéodory map  is said to be
is said to be  -Carathéodory if
-Carathéodory if
-
(iii)
for each real number
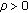 , there exists a function
, there exists a function 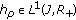 such that
such that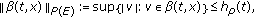 (2.12)
(2.12)
for a.e.  and for all
and for all 
Definition 2.6.
A multivalued operator  is called
is called
-
(a)
 -Lipschitz if and only if there exists
-Lipschitz if and only if there exists  such that
such that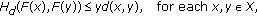 (2.13)
(2.13)
-
(b)
contraction if and only if it is
 -Lipschitz with
-Lipschitz with 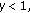
-
(c)
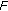 has a fixed point if there exists
has a fixed point if there exists 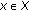 such that
such that 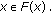
The fixed point set of the multivalued operator  will be denoted by
will be denoted by 
For more details on multivalued maps and the proof of the known results cited in this section we refer interested reader to the books of Deimling [31], Gorniewicz [32], and Hu and Papageorgiou [33].
Essential for the main results of this paper, we state a generalization of Gronwall's lemma for singular kernels [34, Lemma 7.1.1].
Lemma 2.7.
Let  be continuous functions. If
be continuous functions. If  is nondecreasing and there are constants
is nondecreasing and there are constants  and
and  such that
such that

then there exists a constant  such that
such that

for every 
In the sequel, the following fixed point theorems will be used. The following fixed point theorem for contraction multivalued maps is due to Covitz and Nadler [35].
Theorem 2.8.
Let  be a complete metric space. If
be a complete metric space. If  is a contraction, then
is a contraction, then 
The nonlinear alternative of Leray-Schauder applied to completely continuous operators [36].
Theorem 2.9.
Let  be a Banach space, and
be a Banach space, and  convex with
convex with  . Let
. Let  be a completely continuous operator. Then either
be a completely continuous operator. Then either
-
(a)
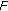 has a fixed point, or
has a fixed point, or -
(b)
the set
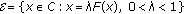 is unbounded.
is unbounded.
The following is the multivalued version of the previous theorem due to Martelli [37].
Theorem 2.10.
Let  be an upper semicontinuous and completely continuous multivalued map. If the set
be an upper semicontinuous and completely continuous multivalued map. If the set

is bounded, then  has a fixed point.
has a fixed point.
To state existence results for perturbed differential equations and inclusions we will use the following fixed point theorem of Krasnoselskii-Scheafer type of the sum of a completely continuous operator and a contraction one due to Burton and Kirk [38].
Theorem 2.11.
Let  be a Banach space, and
be a Banach space, and  two operators satisfying
two operators satisfying
-
(i)
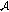 is a contraction;
is a contraction; -
(ii)
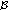 is completely continuous.
is completely continuous.
Then either
-
(a)
the operator equation
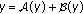 has a solution, or
has a solution, or -
(b)
the set
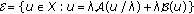 is unbounded for
is unbounded for 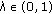 .
.
Recently Dhage states the multivalued version of the previous theorem.
Let  be a Banach space,
be a Banach space,  and
and  two multivalued operators satisfying
two multivalued operators satisfying
-
(a)
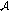 is a contraction;
is a contraction; -
(b)
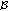 is completely continuous.
is completely continuous.
Then either
-
(i)
The operator inclusion
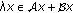 has a solution for
has a solution for 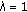 , or
, or -
(ii)
the set
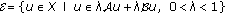 is unbounded.
is unbounded.
In the literature devoted to equations with finite delay, the phase space is much of time the space of all continuous functions on  ,
,  , endowed with the uniform norm topology. When the delay is infinite, the notion of the phase space plays an important role in the study of both qualitative and quantitative theory, a usual choice is a seminormed space
, endowed with the uniform norm topology. When the delay is infinite, the notion of the phase space plays an important role in the study of both qualitative and quantitative theory, a usual choice is a seminormed space  introduced by Hale and Kato [41] and satisfying the following axioms.
introduced by Hale and Kato [41] and satisfying the following axioms.
-
(A1) There exist a positive constant
 and functions
and functions 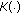 ,
, 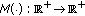 with
with 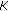 continuous and
continuous and  locally bounded, such that for any
locally bounded, such that for any 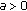 , if
, if  ,
, 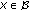 , and
, and 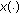 is continuous on
is continuous on 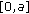 , then for every
, then for every 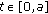 the following conditions hold:
the following conditions hold:-
(i)
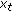 is in
is in 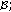
-
(ii)
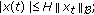
-
(iii)
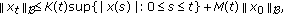 and
and 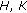 , and
, and  are independent of
are independent of 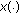 .
.
-
(i)
-
(A2) For the function
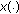 in
in 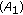 ,
, 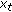 is a
is a  -valued continuous function on
-valued continuous function on 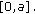
-
(A3) The space
 is complete.
is complete. -
Denote by
 (2.17)
(2.17)
Hereafter are some examples of phase spaces. For other details we refer, for instance, to the book by Hino et al. [42].
Example 2.13.
The spaces  , and
, and  .
.
BC is the space of bounded continuous functions defined from  to
to 
BUC is the space of bounded uniformly continuous functions defined from  to
to 


We have that the spaces  , and
, and  satisfy conditions
satisfy conditions  .
.  satisfies
satisfies  but
but  is not satisfied.
is not satisfied.
Example 2.14.
The spaces  , and
, and  .
.
Let  be a positive continuous function on
be a positive continuous function on  . We define
. We define

We consider the following condition on the function  .
.
For all 
Then we have that the spaces  and
and  satisfy conditions
satisfy conditions  . They satisfy conditions
. They satisfy conditions  and
and  if
if  holds.
holds.
Example 2.15.
The space  .
.
For any real constant  , we define the functional space
, we define the functional space  bys
bys

endowed with the following norm

Then in the space  the axioms
the axioms  are satisfied.
are satisfied.
3. Semilinear Functional Differential Equations
3.1. Introduction
Functional differential and partial differential equations arise in many areas of applied mathematics and such equations have received much attention in recent years. A good guide to the literature for functional differential equations is the books by Hale [43] and Hale and Verduyn Lunel [44], Kolmanovskii and Myshkis [45], and Wu [46] and the references therein.
In a series of papers (see [47–50]), the authors considered some classes of initial value problems for functional differential equations involving the Riemann-Liouville and Caputo fractional derivatives of order  In [51, 52] some classes of semilinear functional differential equations involving the Riemann-Liouville have been considered. For more details on the geometric and physical interpretation for fractional derivatives of both the Riemann-Liouville and Caputo types see [53, 54].
In [51, 52] some classes of semilinear functional differential equations involving the Riemann-Liouville have been considered. For more details on the geometric and physical interpretation for fractional derivatives of both the Riemann-Liouville and Caputo types see [53, 54].
In the following, we consider the semilinear functional differential equation of fractional order of the form


where  is the standard Riemann-Liouville fractional derivative,
is the standard Riemann-Liouville fractional derivative,  is a continuous function,
is a continuous function,  is a closed linear operator (possibly unbounded),
is a closed linear operator (possibly unbounded),  a given continuous function with
a given continuous function with  , and
, and  a real Banach space. For any function
a real Banach space. For any function  defined on
defined on  and any
and any  we denote by
we denote by  the element of
the element of  defined by
defined by

Here  represents the history of the state from time
represents the history of the state from time  , up to the present time
, up to the present time  .
.
The reason for studying (3.1) is that it appears in mathematical models of viscoelasticity [55], and in other fields of science [54, 56]. Equation (3.1) is equivalent to solve an integral equation of convolution type. It is also of interest to explore the neighborhood of the diffusion ( ). In this survey paper, we use the fractional derivative in the Riemann-Liouville sense. The problems considered in the survey are subject to zero data, which in this case, the Riemann-Liouville and Caputo fractional derivatives coincide. From a practical point of view, in some mathematical models it is more appropriate to consider traditional initial or boundary data. This is what we are considering in this survey.
). In this survey paper, we use the fractional derivative in the Riemann-Liouville sense. The problems considered in the survey are subject to zero data, which in this case, the Riemann-Liouville and Caputo fractional derivatives coincide. From a practical point of view, in some mathematical models it is more appropriate to consider traditional initial or boundary data. This is what we are considering in this survey.
In all our paper we suppose that the operator  is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup
-semigroup  . Denote by
. Denote by

Before stating our main results in this section for problem (3.1) and (3.2) we give the definition of the mild solution.
Definition 3.1 (see [23]).
One says that a continuous function  is a mild solution of problem (3.1) and (3.2) if
is a mild solution of problem (3.1) and (3.2) if  and
and

3.2. Existence Results for Finite Delay
By using the Banach's contraction principle, we get the following existence result for problem (3.1) and (3.2).
Theorem 3.2.
Let  continuous. Assume the following.
continuous. Assume the following.
-
(H1) There exists a nonnegative constant
 such that
such that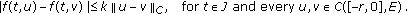 (3.6)
(3.6)
Then there exists a unique mild solution of problem (3.1) and (3.2) on 
Proof.
Transform the IVP (3.1) and (3.2) into a fixed point problem. Consider the operator  defined by
defined by

Let us define the iterates of operator  by
by

It will be sufficient to prove that  is a contraction operator for
is a contraction operator for  sufficiently large. For every
sufficiently large. For every  we have
we have

Indeed,

Therefore (3.9) is proved for  . Assuming by induction that (3.9) is valid for
. Assuming by induction that (3.9) is valid for  , then
, then

and then (3.9) follows for  .
.
Now, taking  sufficiently large in (3.9) yield the contraction of operator
sufficiently large in (3.9) yield the contraction of operator  .
.
Consequently  has a unique fixed point by the Banach's contraction principle, which gives rise to a unique mild solution to the problem (3.1) and (3.2).
has a unique fixed point by the Banach's contraction principle, which gives rise to a unique mild solution to the problem (3.1) and (3.2).
The following existence result is based upon Theorem 2.9.
Theorem 3.3.
Assume that the following hypotheses hold.
-
(H2) The semigroup
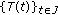 is compact for
is compact for 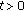 .
. -
(H3) There exist functions
 such that
such that (3.12)
(3.12)
Then the problem (3.1) and (3.2) has at least one mild solution on 
Proof.
Transform the IVP (3.1) and (3.2) into a fixed point problem. Consider the operator  as defined in Theorem 3.2. To show that
as defined in Theorem 3.2. To show that  is continuous, let us consider a sequence
is continuous, let us consider a sequence  such that
such that  in
in  . Then
. Then

Since  is a continuous function, then we have
is a continuous function, then we have

Thus  is continuous. Now for any
is continuous. Now for any  , and each
, and each  we have for each
we have for each 

Thus  maps bounded sets into bounded sets in
maps bounded sets into bounded sets in  .
.
Now, let  ,
,  Thus if
Thus if  and
and  we have for any
we have for any 

As  and
and  sufficiently small, the right-hand side of the above inequality tends to zero, since
sufficiently small, the right-hand side of the above inequality tends to zero, since  is a strongly continuous operator and the compactness of
is a strongly continuous operator and the compactness of  for
for  implies the continuity in the uniform operator topology [29]. By the Arzelá-Ascoli theorem it suffices to show that
implies the continuity in the uniform operator topology [29]. By the Arzelá-Ascoli theorem it suffices to show that  maps
maps  into a precompact set in
into a precompact set in  .
.
Let  be fixed and let
be fixed and let  be a real number satisfying
be a real number satisfying  . For
. For  we define
we define

Since  is a compact operator for
is a compact operator for  , the set
, the set

is precompact in  for every
for every  Moreover
Moreover

Therefore, the set  is precompact in
is precompact in  . Hence the operator
. Hence the operator  is completely continuous. Now, it remains to show that the set
is completely continuous. Now, it remains to show that the set

is bounded.
Let  be any element. Then, for each
be any element. Then, for each  ,
,

Then

We consider the function defined by

Let  such that
such that  , if
, if  then by (3.22) we have, for
then by (3.22) we have, for  (note
(note  )
)

If  then
then  and the previous inequality holds.
and the previous inequality holds.
By Lemma 2.7 we have

Hence

This shows that the set  is bounded. As a consequence of Theorem 2.9, we deduce that the operator
is bounded. As a consequence of Theorem 2.9, we deduce that the operator  has a fixed point which is a mild solution of the problem (3.1) and (3.2).
has a fixed point which is a mild solution of the problem (3.1) and (3.2).
3.3. An Example
As an application of our results we consider the following partial functional differential equation of the form

where  is continuous and
is continuous and  is a given function.
is a given function.
Let

Take  and define
and define  by
by  with domain
with domain

Then

where  is the inner product in
is the inner product in  and
and  is the orthogonal set of eigenvectors in
is the orthogonal set of eigenvectors in  It is well known (see [29]) that
It is well known (see [29]) that  is the infinitesimal generator of an analytic semigroup
is the infinitesimal generator of an analytic semigroup  in
in  and is given by
and is given by

Since the analytic semigroup  is compact, there exists a constant
is compact, there exists a constant  such that
such that

Also assume that there exist continuous functions  such that
such that

We can show that problem (3.1) and (3.2) is an abstract formulation of problem (3.27). Since all the conditions of Theorem 3.3 are satisfied, the problem (3.27) has a solution  on
on 
3.4. Existence Results for Infinite Delay
In the following we will extend the previous results to the case when the delay is infinite. More precisely we consider the following problem

where  is the standard Riemann-Liouville fractional derivative,
is the standard Riemann-Liouville fractional derivative,  is a continuous function,
is a continuous function,  the phase space [41],
the phase space [41],  is the infinitesimal generator of a strongly continuous semigroup
is the infinitesimal generator of a strongly continuous semigroup  ,
,  a continuous function with
a continuous function with  and
and  a real Banach space. For any
a real Banach space. For any  the function
the function  is defined by
is defined by

Consider the following space:

where  is the restriction of
is the restriction of  to
to  Let
Let  be the seminorm in
be the seminorm in  defined by
defined by

Definition 3.4.
One says that a function  is a mild solution of problem (3.34) if
is a mild solution of problem (3.34) if  and
and

The first existence result is based on Banach's contraction principle.
Theorem 3.5.
Assume the following.
-
(H4) There exists a nonnegative constant
 such that
such that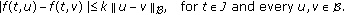 (3.39)
(3.39)
Then there exists a unique mild solution of problem (3.34) on 
Proof.
Transform the IVP (3.34) into a fixed point problem. Consider the operator  defined by
defined by

For  , we define the function
, we define the function

Then  . Set
. Set

It is obvious that  satisfies (3.38) if and only if
satisfies (3.38) if and only if  satisfies
satisfies  and
and

Let

For any  , we have
, we have

Thus  is a Banach space. Let the operator
is a Banach space. Let the operator  defined by
defined by

It is obvious that  has a fixed point is equivalent to
has a fixed point is equivalent to  has a fixed point, and so we turn to proving that
has a fixed point, and so we turn to proving that  has a fixed point. As in Theorem 3.2, we show by induction that
has a fixed point. As in Theorem 3.2, we show by induction that  satisfy for any
satisfy for any  , the following inequality:
, the following inequality:

which yields the contraction of  for sufficiently large values of
for sufficiently large values of  . Therefore, by the Banach's contraction principle
. Therefore, by the Banach's contraction principle  has a unique fixed point
has a unique fixed point  . Then
. Then  is a fixed point of the operator
is a fixed point of the operator  , which gives rise to a unique mild solution of the problem (3.34).
, which gives rise to a unique mild solution of the problem (3.34).
Next we give an existence result based upon the nonlinear alternative of Leray-Schauder type.
Theorem 3.6.
Assume that the following hypotheses hold.
-
(H5) The semigroup
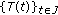 is compact for
is compact for  .
. -
(H6) There exist functions
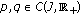 such that
such that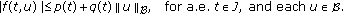 (3.48)
(3.48)
Then, the problem (3.34) has at least one mild solution on 
Proof.
Transform the IVP (3.34) into a fixed point problem. Consider the operator  defined as in Theorem 3.5. We will show that the operator
defined as in Theorem 3.5. We will show that the operator  is continuous and completely continuous. Let
is continuous and completely continuous. Let  be a sequence such that
be a sequence such that  in
in  . Then
. Then

Since  is a continuous function, then we have
is a continuous function, then we have

Thus  is continuous. To show that
is continuous. To show that  maps bounded sets into bounded sets in
maps bounded sets into bounded sets in  it is enough to show that for any
it is enough to show that for any  there exists a positive constant
there exists a positive constant  such that for each
such that for each  we have
we have  Let
Let  , then
, then

Then we have for each 

Taking the supremum over  we have
we have

Now let  ,
,  thus if
thus if  and
and  we have for each
we have for each 

As  and
and  sufficiently small, the right-hand side of the above inequality tends to zero, since
sufficiently small, the right-hand side of the above inequality tends to zero, since  is a strongly continuous operator and the compactness of
is a strongly continuous operator and the compactness of  for
for  implies the continuity in the uniform operator topology (see [29]). By the Arzelá-Ascoli theorem it suffices to show that
implies the continuity in the uniform operator topology (see [29]). By the Arzelá-Ascoli theorem it suffices to show that  maps
maps  into a precompact set in
into a precompact set in  . Let
. Let  be fixed and let
be fixed and let  be a real number satisfying
be a real number satisfying  . For
. For  we define
we define

Since  is a compact operator for
is a compact operator for  , the set
, the set

is precompact in  for every
for every  Moreover
Moreover

Therefore, the set  is precompact in
is precompact in  . Hence the operator
. Hence the operator  is completely continuous. Now, it remains to show that the set
is completely continuous. Now, it remains to show that the set

is bounded. Let  be any element. Then, for each
be any element. Then, for each  ,
,

Then

but

Take the right-hand side of the above inequality as  , then by (3.60) we have
, then by (3.60) we have

Using the above inequality and the definition of  we have
we have

By Lemma 2.7, there exists a constant  such that we have
such that we have

Then there exists a constant  such that
such that  This shows that the set
This shows that the set  is bounded. As a consequence of the Leray-Schauder Theorem, we deduce that the operator
is bounded. As a consequence of the Leray-Schauder Theorem, we deduce that the operator  has a fixed point, then
has a fixed point, then  has one which gives rise to a mild solution of the problem (3.34).
has one which gives rise to a mild solution of the problem (3.34).
3.5. An Example
To illustrate the previous results, we consider in this section the following model:

where  are continuous functions.
are continuous functions.
Consider  and define
and define  by
by  with domain
with domain

Then  generates a
generates a  semigroup
semigroup  (see [29]).
(see [29]).
For the phase space  , we choose the well-known space
, we choose the well-known space  : the space of uniformly bounded continuous functions endowed with the following norm:
: the space of uniformly bounded continuous functions endowed with the following norm:

If we put for  and
and 

Then, problem (3.65) takes the abstract neutral evolution form (3.34).
4. Semilinear Functional Differential Equations of Neutral Type
4.1. Introduction
Neutral differential equations arise in many areas of applied mathematics, an extensive theory is developed, we refer the reader to the book by Hale and Verduyn Lunel [44] and Kolmanovskii and Myshkis [45]. The work for neutral functional differential equations with infinite delay was initiated by Hernández and Henríquez in [57, 58]. In the following, we will extend such results to arbitrary order functional differential equations of neutral type with finite as well as infinite delay. We based our main results upon the Banach's principle and the Leray-Schauder theorem.
4.2. Existence Results for the Finite Delay
First we will be concerned by the case when the delay is finite, more precisely we consider the following class of neutral functional differential equations

Definition 4.1.
One says that a function  is a mild solution of problem (4.1) if
is a mild solution of problem (4.1) if  and
and

Our first existence result is based on the Banach's contraction principle.
Theorem 4.2.
Assume the following.
-
(H7) There exists a nonnegative constant
 such that
such that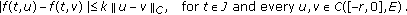 (4.3)
(4.3)
-
(H8) There exists a nonnegative constant
 such that
such that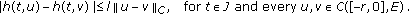 (4.4)
(4.4)
Then there exists a unique mild solution of problem (4.1) on 
Proof.
Transform the IVP (4.1) into a fixed point problem. Consider the operator  defined by
defined by

As in Theorem 3.2, we show by induction that  satisfy for any
satisfy for any  , the following inequality:
, the following inequality:

which yields the contraction of  for sufficiently large values of
for sufficiently large values of  . Therefore, by the Banach's contraction principle
. Therefore, by the Banach's contraction principle  has a unique fixed point which gives rise to unique mild solution of problem (4.1).
has a unique fixed point which gives rise to unique mild solution of problem (4.1).
Next we give an existence result using the nonlinear alternative of Leray-Schauder.
Theorem 4.3.
Assume that the following hypotheses hold.
-
(H9) The semigroup
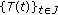 is compact for
is compact for 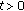 .
. -
(H10) There exist functions
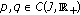 such that
such that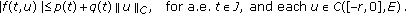 (4.7)
(4.7) -
(H11) The function
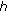 is continuous and completely continuous, and for every bounded set
is continuous and completely continuous, and for every bounded set 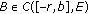 , the set
, the set 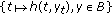 is equicontinuous in
is equicontinuous in 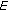 .
. -
(H12) There exists constants:
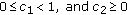 such that
such that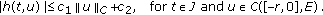 (4.8)
(4.8)
Then the problem (4.1) has at least one mild solution on 
Proof.
Consider the operator  as in Theorem 4.2.
as in Theorem 4.2.
To show that the operator  is continuous and completely continuous it suffices to show, using
is continuous and completely continuous it suffices to show, using  , that the operator
, that the operator  defined by
defined by

is continuous and completely continuous. This can be done following the proof of Theorem 3.3.
Now, it remains to show that the set

is bounded. Let  be any element. Then, for each
be any element. Then, for each  ,
,

We consider the function defined by

Let  such that
such that  , If
, If  then we have, for
then we have, for  (note
(note  )
)

If  then
then  and the previous inequality holds.
and the previous inequality holds.
By Lemma 2.7 there exists  such that
such that

This shows that the set  is bounded. As a consequence of the Leray-Schauder Theorem, we deduce that the operator
is bounded. As a consequence of the Leray-Schauder Theorem, we deduce that the operator  has a fixed point which gives rise to a mild solution of the problem (4.1).
has a fixed point which gives rise to a mild solution of the problem (4.1).
4.3. Existence Results for the Infinite Delay
In the following we will extend our previous results to the case of infinite delay, more precisely we consider the following problem:

Our first existence result is based on the Banach's contraction principle.
Theorem 4.4.
Assume that the following hypotheses hold.
-
(H13) There exists a nonnegative constant
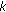 such that
such that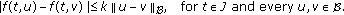 (4.16)
(4.16) -
(H14) There exists a nonnegative constant
 such that
such that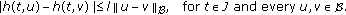 (4.17)
(4.17)
Then there exists a unique mild solution of problem (4.15) on 
Proof.
Consider the operator  defined by
defined by

In analogy to Theorem 3.2, we consider the operator  defined by
defined by

As in Theorem 3.2, we show by induction that  satisfy for any
satisfy for any  , the following inequality:
, the following inequality:

which yields the contraction of  for sufficiently large values of
for sufficiently large values of  . Therefore, by the Banach's contraction principle
. Therefore, by the Banach's contraction principle  has a unique fixed point
has a unique fixed point  . Then
. Then  is a fixed point of the operator
is a fixed point of the operator  , which gives rise to a unique mild solution of the problem (4.15).
, which gives rise to a unique mild solution of the problem (4.15).
Next we give an existence result based upon the the nonlinear alternative of Leray-Schauder.
Theorem 4.5.
Assume that the following hypotheses hold.
-
(H15) The semigroup
 is compact for
is compact for  .
. -
(H16) There exist functions
 such that
such that (4.21)
(4.21) -
(H17) The function
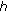 is continuous and completely continuous, and for every bounded set
is continuous and completely continuous, and for every bounded set  , the set
, the set 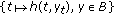 is equicontinuous in
is equicontinuous in 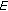 .
. -
(H18) There exists constants:
 such that
such that (4.22)
(4.22)
Then the problem (4.15) has at least one mild solution on 
Proof.
Let  defined as in Theorem 4.4. We can easily show that the operator
defined as in Theorem 4.4. We can easily show that the operator  is continuous and completely continuous. Using
is continuous and completely continuous. Using  it suffices to show that the operator
it suffices to show that the operator  defined by
defined by

is continuous and completely continuous. Now, it remains to show that the set

is bounded.
Let  be any element. Then, for each
be any element. Then, for each  ,
,

Denote  as in Theorem 3.6. Then
as in Theorem 3.6. Then

Then

By Lemma 2.7 there exists a constant  such that
such that

where

Then there exists a constant  such that
such that  This shows that the set
This shows that the set  is bounded. As a consequence of the Leray-Schauder Theorem, we deduce that the operator
is bounded. As a consequence of the Leray-Schauder Theorem, we deduce that the operator  has a fixed point which gives rise to a mild solution of the problem (4.15).
has a fixed point which gives rise to a mild solution of the problem (4.15).
4.4. Example
To illustrate the previous results, we consider the following model arising in population dynamics:

where  and
and  and
and  are continuous functions. Let
are continuous functions. Let  and consider the operator
and consider the operator

defined by

It is well known that  generates a
generates a  -semigroup (see [29]). For the phase space
-semigroup (see [29]). For the phase space  , we choose the well-known space
, we choose the well-known space  : the space of bounded uniformly continuous functions endowed with the following norm:
: the space of bounded uniformly continuous functions endowed with the following norm:

If we put for  and
and 

then (4.30) take the abstract form (4.15). Under appropriate conditions on  , the problem (4.30) has by Theorem 4.5 a solution.
, the problem (4.30) has by Theorem 4.5 a solution.
5. Semilinear Functional Differential Inclusions
Differential inclusions are generalization of differential equations, therefore all problems considered for differential equations, that is, existence of solutions, continuation of solutions, dependence on initial conditions and parameters, are present in the theory of differential inclusions. Since a differential inclusion usually has many solutions starting at a given point, new issues appear, such as investigation of topological properties of the set of solutions, and selection of solutions with given properties.
Functional differential inclusions with fractional order are first considered by El Sayed and Ibrahim [59]. Very recently Benchohra et al. [49], and Ouahab [60] have considered some classes of ordinary functional differential inclusions with delay, and in [6, 61] Agarwal et al. considered a class of boundary value problems for differential inclusion involving Caputo fractional derivative of order  . Chang and Nieto [62] considered a class of fractional differential inclusions of order
. Chang and Nieto [62] considered a class of fractional differential inclusions of order  . Here we continue this study by considering partial functional differential inclusions involving the Riemann-Liouville derivative of order
. Here we continue this study by considering partial functional differential inclusions involving the Riemann-Liouville derivative of order  . The both cases of convex valued and nonconvex valued of the right-hand side are considered, and where the delay is finite as well as infinite. Our approach is based on the
. The both cases of convex valued and nonconvex valued of the right-hand side are considered, and where the delay is finite as well as infinite. Our approach is based on the  -semigroups theory combined with some suitable fixed point theorems.
-semigroups theory combined with some suitable fixed point theorems.
In the following, we will be concerned with fractional semilinear functional differential inclusions with finite delay of the form

where  is the standard Riemann-Liouville fractional derivative.
is the standard Riemann-Liouville fractional derivative.  is a multivalued function.
is a multivalued function.  is the family of all nonempty subsets of
is the family of all nonempty subsets of  .
.  is a densely defined (possibly unbounded) operator generating a strongly continuous semigroup
is a densely defined (possibly unbounded) operator generating a strongly continuous semigroup  of bounded linear operators from
of bounded linear operators from  into
into  is a given continuous function such that
is a given continuous function such that  and
and  is a real separable Banach spaces. For
is a real separable Banach spaces. For  the norm of
the norm of  is defined by
is defined by

For  the norm of
the norm of  is defined by
is defined by

Recall that for each  the set
the set

is known as the set of selections of the multivalued  .
.
Definition 5.1.
One says that a continuous function  is a mild solution of problem (5.1) if there exists
is a mild solution of problem (5.1) if there exists  such that
such that  and
and

In the following, we give our first existence result for problem (5.1) with a convex valued right-hand side. Our approach is based upon Theorem 2.10.
Theorem 5.2.
Assume the following.
-
(H19)
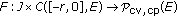 is Carathéodory.
is Carathéodory. -
(H20) The semigroup
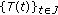 is compact for
is compact for 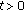 .
. -
(H21) There exist functions
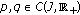 such that
such that (5.6)
(5.6)
Then the problem (5.1) has at least one mild solution.
Proof.
Consider the multivalued operator

defined by  such that
such that

where  It is obvious that fixed points of
It is obvious that fixed points of  are mild solutions of problem (5.1). We will show that
are mild solutions of problem (5.1). We will show that  is a completely continuous multivalued operator, u.s.c. with convex values.
is a completely continuous multivalued operator, u.s.c. with convex values.
It is obvious that  is convex valued for each
is convex valued for each  since
since  has convex values.
has convex values.
To show that  maps bounded sets into bounded sets in
maps bounded sets into bounded sets in  it is enough to show that there exists a positive constant
it is enough to show that there exists a positive constant  such that for each
such that for each  ,
,  one has
one has  Indeed, if
Indeed, if  , then there exists
, then there exists  such that for each
such that for each  we have
we have

Using  we have for each
we have for each  ,
,

Then for each  we have
we have  .
.
Now let  for
for  , and let
, and let  ,
,  If
If  and
and  we have
we have

where  . Using the following semigroup identities
. Using the following semigroup identities

we get

As  and
and  sufficiently small, the right-hand side of the above inequality tends to zero, since
sufficiently small, the right-hand side of the above inequality tends to zero, since  is a strongly continuous operator and the compactness of
is a strongly continuous operator and the compactness of  for
for  implies the continuity in the uniform operator topology [29]. Let
implies the continuity in the uniform operator topology [29]. Let  be fixed and let
be fixed and let  be a real number satisfying
be a real number satisfying  . For
. For  we define
we define

where  . Since
. Since  is a compact operator, the set
is a compact operator, the set

is precompact in  for every
for every  Moreover, for every
Moreover, for every  we have
we have

Therefore, the set  is totally bounded. Hence
is totally bounded. Hence  is precompact in
is precompact in  .
.
As a consequence of the Arzelá-Ascoli theorem we can conclude that the multivalued operator  is completely continuous.
is completely continuous.
Now we show that the operator  has closed graph. Let
has closed graph. Let  ,
,  , and
, and  . We will show that
. We will show that  .
.
 means that there exists
means that there exists  such that
such that

We must show that there exists  such that, for each
such that, for each 

Since  has compact values, there exists a subsequence
has compact values, there exists a subsequence  such that
such that

Since  is u.s.c., then for every
is u.s.c., then for every  , there exist
, there exist  such that for every
such that for every  , we have
, we have

and hence,

Then for each 

Hence,

Now it remains to show that the set

is bounded. Let  be any element, then there exists
be any element, then there exists  such that
such that

Then by (H20) and (H21) for each  we have
we have

Consider the function defined by

Let  such that
such that  , If
, If  then we have, for
then we have, for  (note
(note  )
)

If  then
then  and the previous inequality holds.
and the previous inequality holds.
By Lemma 2.7 we have

Taking the supremum over  we get
we get

Hence

and so, the set  is bounded. Consequently the multivalued operator
is bounded. Consequently the multivalued operator  has a fixed point which gives rise to a mild solution of problem (5.1) on
has a fixed point which gives rise to a mild solution of problem (5.1) on 
Now we will be concerned with existence results for problem (5.1) with nonconvex valued right-hand side. Our approach is based on the fixed point theorem for contraction multivalued maps due to Covitz and Nadler Jr. [35].
Theorem 5.3.
Assume that (H19) holds.
There exists  such that
such that

with

If

then the problem (5.1) has at least one mild solution on 
Proof.
First we will prove that  for each
for each  .
.  such that
such that  in
in  . Then
. Then  and there exists
and there exists  such that for each
such that for each 

Using the compactness property of the values of  and the second part of
and the second part of  we may pass to a subsequence if necessary to get that
we may pass to a subsequence if necessary to get that  converges weakly to
converges weakly to  (the space endowed with the weak topology). From Mazur's lemma (see [63]) there exists
(the space endowed with the weak topology). From Mazur's lemma (see [63]) there exists

then there exists a subsequence  in
in  such that
such that  converges strongly to
converges strongly to  in
in  Then for each
Then for each  ,
,

So, 
Now Let  and
and  . Then there exists
. Then there exists  such that
such that

Then from  there is
there is  such that
such that

Consider the multivalued operator  defined by
defined by

Since the multivalued operator  is measurable (see [64, proposition III4]) there exists
is measurable (see [64, proposition III4]) there exists  a measurable selection for
a measurable selection for  . So,
. So,  and
and

Let us define for each 

Then we have

For  , the previous inequality is satisfied. Taking the supremum over
, the previous inequality is satisfied. Taking the supremum over  we get
we get

By analogous relation, obtained by interchanging the roles of  and
and  , it follows that
, it follows that

By (5.34)  is a contraction, and hence Theorem 2.8 implies that
is a contraction, and hence Theorem 2.8 implies that  has a fixed point which gives rise to a mild solution of problem (5.1).
has a fixed point which gives rise to a mild solution of problem (5.1).
In the following, we will extend the previous results to the case when the delay is infinite. More precisely we consider the following problem:

where  is the standard Riemann-Liouville fractional derivative.
is the standard Riemann-Liouville fractional derivative.  is a multivalued function.
is a multivalued function.  is the phase space [41],
is the phase space [41],  is the infinitesimal generator of a strongly continuous semigroup
is the infinitesimal generator of a strongly continuous semigroup  ,
,  a continuous function with
a continuous function with  and
and  a real Banach space. Consider the following space:
a real Banach space. Consider the following space:

where  is the restriction of
is the restriction of  to
to  Let
Let  be the seminorm in
be the seminorm in  defined by
defined by

Definition 5.4.
One says that a function  is a mild solution of problem (5.46) if
is a mild solution of problem (5.46) if  and there exists
and there exists  such that
such that

In the following, we give an existence result for problem (5.46) with convex valued right-hand side. Our approach is based upon Theorem 2.10.
Theorem 5.5.
Assume the following.
-
(H23)
 is Carathéodory.
is Carathéodory. -
(H24) The semigroup
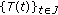 is compact for
is compact for 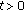 .
. -
(H25) There exist functions
 such that
such that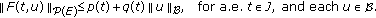 (5.50)
(5.50)
Then the problem (5.46) has at least one mild solution.
Proof.
Consider the operator

defined by

where  .
.
For  , we define the function
, we define the function

Then  . Set
. Set

It is obvious that  satisfies (5.49) if and only if
satisfies (5.49) if and only if  satisfies
satisfies  and
and

Let

For any  , we have
, we have

Thus  is a Banach space. Let the operator
is a Banach space. Let the operator  defined by
defined by

where  .
.
As in Theorem 5.2, we can show that the multivalued operator  is completely continuous, u.s.c. with convex values. It remains to show that the set
is completely continuous, u.s.c. with convex values. It remains to show that the set

is bounded.
Let  be any element, then there exists a selection
be any element, then there exists a selection  such that
such that

Then for each  we have
we have

Following the proof of Theorem 3.6, we can show that the set  is bounded. Consequently, the multivalued operator
is bounded. Consequently, the multivalued operator  has a fixed point. Then
has a fixed point. Then  has one, witch gives rise to a mild solution of problem (5.46).
has one, witch gives rise to a mild solution of problem (5.46).
Now we give an existence result for problem (5.46) with nonconvex valued right-hand side by using the fixed point Theorem 2.8.
Theorem 5.6.
Assume that (H23) holds. Then
-
(H26) There exists
 such that
such that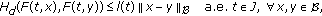 (5.62)
(5.62)
with

If

then the problem (5.46) has at least one mild solution on 
Proof.
As the previous theorem and following steps of the proof of Theorem 5.3.
6. Perturbed Semilinear Differential Equations and Inclusions
In this section, we will be concerned with semilinear functional differential equations and inclusion of fractional order and where a perturbed term is considered. Our approach is based upon Burton-Kirk fixed point theorem (Theorem 2.11).
First, consider equations of the form

Definition 6.1.
One says that a continuous function  is a mild solution of problem (6.1) if
is a mild solution of problem (6.1) if  and
and

Our first main result in this section reads as follows.
Theorem 6.2.
Assume that the following hypotheses hold.
-
(H27) The semigroup
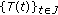 is compact for
is compact for 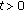 .
. -
(H28) There exist functions
 such that
such that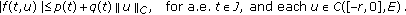 (6..3)
(6..3) -
(H29) There exists a nonnegative constant
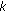 such that
such that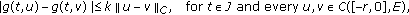 (6..4)
(6..4)

then the problem (6.1) has at least one mild solution on 
Proof.
Transform the problem (6.1) into a fixed point problem. Consider the two operators

defined by

Then the problem of finding the solution of IVP (6.1) is reduced to finding the solution of the operator equation  We will show that the operators
We will show that the operators  and
and  satisfies all conditions of Theorem 2.11.
satisfies all conditions of Theorem 2.11.
From Theorem 3.6, the operator  is completely continuous. We will show that the operator
is completely continuous. We will show that the operator  is a contraction. Let
is a contraction. Let  , then for each
, then for each 

Taking the supremum over  ,
,

which implies by (6.5) that  is a contraction. Now, it remains to show that the set
is a contraction. Now, it remains to show that the set

is bounded.
Let  be any element. Then, for each
be any element. Then, for each  ,
,

Then

where

We consider the function defined by

Let  such that
such that  . If
. If  then by the previous inequality we have, for
then by the previous inequality we have, for  (note
(note  )
)

If  then
then  and the previous inequality holds.
and the previous inequality holds.
By Lemma 2.7, there exists a constant  such that we have
such that we have

Hence,

This shows that the set  is bounded. as a consequence of the Theorem 2.11, we deduce that the operator
is bounded. as a consequence of the Theorem 2.11, we deduce that the operator  has a fixed point which gives rise to a mild solution of the problem (6.1).
has a fixed point which gives rise to a mild solution of the problem (6.1).
Now we consider multivalued functional differential equations of the form

Definition 6.3.
One says that a continuous function  is a mild solution of problem (6.18) if
is a mild solution of problem (6.18) if  and there exist
and there exist  and
and  such that
such that

Theorem 6.4.
Assume that the following hypotheses hold.
-
(H30) The semigroup
 is compact for
is compact for  .
. -
(H31) The multifunction
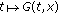 is measurable, convex valued and integrably bounded for each
is measurable, convex valued and integrably bounded for each  .
. -
(H32) There exists a function
 such that
such that (6..20)
(6..20) -
with
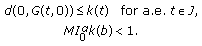 (6..21)
(6..21) -
(H33)
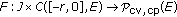 is Carathéodory.
is Carathéodory. -
(H34) There exist functions
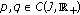 such that
such that (6..22)
(6..22)
Then IVP (6.18) has at least one mild solution on  .
.
Proof.
Consider the two multivalued operators

defined by  such that
such that

defined by  such that
such that

where  and
and  . We will show that the operator
. We will show that the operator  is closed, convex, and bounded valued and it is a contraction. Let
is closed, convex, and bounded valued and it is a contraction. Let  such that
such that  in
in  . Using (H31), we can show that the values of Niemysky operator
. Using (H31), we can show that the values of Niemysky operator  are closed in
are closed in  , and hence
, and hence  is closed for each
is closed for each 
Now let  , then there exists
, then there exists  such that, for each
such that, for each  we have
we have

Let  Then, for each
Then, for each  , we have
, we have

Since  has convex values, one has
has convex values, one has

and hence  is convex for each
is convex for each 
Let  be any element. Then, there exists
be any element. Then, there exists  such that
such that

By (H31), we have for all 

where  is from Definition 2.4. Then
is from Definition 2.4. Then  for all
for all  . Hence
. Hence  is a bounded subset of
is a bounded subset of  .
.
As in Theorem 5.3, we can easily show that the multivalued operator  is a contraction. Now, as in Theorem 5.2 we can show that the operator
is a contraction. Now, as in Theorem 5.2 we can show that the operator  satisfies all the conditions of Theorem 2.12.
satisfies all the conditions of Theorem 2.12.
It remains to show that the set

is bounded.
Let  be any element. Then there exists
be any element. Then there exists  and
and  such that for each
such that for each  ,
,

Then

where

We consider the function defined by

Let  such that
such that  . If
. If  then by the previous inequality we have, for
then by the previous inequality we have, for  (note
(note  )
)

If  then
then  and the previous inequality holds.
and the previous inequality holds.
By Lemma 2.7, there exists a constant  such that we have
such that we have

Hence

This shows that the set  is bounded. As a result, the conclusion (ii) of Theorem 2.12 does not hold. Hence, the conclusion (i) holds and consequently
is bounded. As a result, the conclusion (ii) of Theorem 2.12 does not hold. Hence, the conclusion (i) holds and consequently  has a fixed point which is a mild solution of problem (6.18).
has a fixed point which is a mild solution of problem (6.18).
7. Some Existence Results in Ordered Banach Spaces
In this section, we present some existence results in ordered Banach spaces using the method of upper and lower mild solutions. Before stating our main results let us introduce some preliminaries.
Definition 7.1.
A nonempty closed subset  of a Banach space
of a Banach space  is said to be a cone if
is said to be a cone if
-
(i)
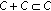 ,
, -
(ii)
 for
for 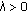 ,
, -
(iii)
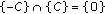 .
.
A cone  is called normal if the norm
is called normal if the norm  is semimonotone on
is semimonotone on  , that is, there exists a constant
, that is, there exists a constant  such that
such that  whenever
whenever  . We equip the space
. We equip the space  with the order relation
with the order relation  induced by a regular cone
induced by a regular cone  in
in  , that is for all
, that is for all  if and only if
if and only if  In what follows will assume that the cone
In what follows will assume that the cone  is normal. Cones and their properties are detailed in [65, 66]. Let
is normal. Cones and their properties are detailed in [65, 66]. Let  be such that
be such that  . Then, by an order interval
. Then, by an order interval  we mean a set of points in
we mean a set of points in  given by
given by

Definition 7.2.
Let  be an ordered Banach space. A mapping
be an ordered Banach space. A mapping  is called increasing if
is called increasing if  for any
for any  with
with  . Similarly,
. Similarly,  is called decreasing if
is called decreasing if  whenever
whenever  .
.
Definition 7.3.
A function  is called increasing in
is called increasing in  for
for  , if
, if  for each
for each  for all
for all  with
with  . Similarly
. Similarly  is called decreasing in
is called decreasing in  for
for  , if
, if  for each
for each  for all
for all  with
with  .
.
Now suppose that  is an ordered Banach space and reconsider the initial value problem (3.1) and (3.2) with the same data.
is an ordered Banach space and reconsider the initial value problem (3.1) and (3.2) with the same data.
Definition 7.4.
One says that a continuous function  is a lower mild solution of problem (3.1) and (3.2) if
is a lower mild solution of problem (3.1) and (3.2) if  and
and

Similarly an upper mild solution  of IVP (3.1) and (3.2) is defined by reversing the order.
of IVP (3.1) and (3.2) is defined by reversing the order.
The following fixed point theorem is crucial for our existence result.
Theorem 7.5 (see [66]).
Let  be a normal cone in a partially ordered Banach space
be a normal cone in a partially ordered Banach space  . Let
. Let  be increasing on the interval
be increasing on the interval  and transform
and transform  into itself, that is,
into itself, that is,  and
and  . Assume further that
. Assume further that  is continuous and completely continuous. Then
is continuous and completely continuous. Then  has at least one fixed point
has at least one fixed point  .
.
Our first main result reads as follows.
Theorem 7.6.
Assume that assumptions (H2)-(H3) hold. Assume moreover that
-
(H35) The function
 is increasing in
is increasing in  for each
for each 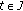 .
. -
(H36)
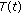 is order-preserving, that is,
is order-preserving, that is, 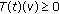 whenever
whenever 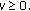
-
(H37) The IVP (3.1) and (3.2) has a lower mild solution
 and an upper mild solution
and an upper mild solution  with
with 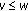 .
.
Then IVP (3.1) and (3.2) has at least one mild solution  on
on  with
with 
Proof.
It can be shown, as in the proof of Theorem 3.2, that  is continuous and completely continuous on
is continuous and completely continuous on  . We will show that
. We will show that  is increasing on
is increasing on  . Let
. Let  be such that
be such that  Then by (H35),(H36), we have for each
Then by (H35),(H36), we have for each 

Therefore  is increasing on
is increasing on  . Finally, let
. Finally, let  be any element. By (H37), we deduce that
be any element. By (H37), we deduce that

which shows that  for all
for all  . Thus, the functions
. Thus, the functions  satisfies all conditions of Theorem 7.5, and hence IVP (3.1) and (3.2) has a mild solution on
satisfies all conditions of Theorem 7.5, and hence IVP (3.1) and (3.2) has a mild solution on  belonging to the interval
belonging to the interval  .
.
Now reconsider the perturbed initial value problem (6.1). To state our second main result in this section we use the following fixed point theorem due to Dhage and Henderson.
Theorem 7.7 (see [67]).
Let  be an order interval in a Banach space and let
be an order interval in a Banach space and let  be two functions satisfying
be two functions satisfying
-
(a)
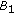 is a contraction,
is a contraction, -
(b)
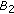 is completely continuous,
is completely continuous, -
(c)
 and
and 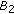 are strictly monotone increasing,
are strictly monotone increasing, -
(d)
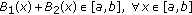 .
.
Further if the cone  in
in  is normal, then the equation
is normal, then the equation  has at least fixed point
has at least fixed point  and a greatest fixed point
and a greatest fixed point  . Moreover
. Moreover  and
and  , where
, where  and
and  are the sequences in
are the sequences in  defined by
defined by

We need the following definitions in the sequel.
Definition 7.8.
One says that a continuous function  is a lower mild solution of problem (6.1)
is a lower mild solution of problem (6.1)  and
and

Similarly an upper mild solution  of IVP (6.1) is defined by reversing the order.
of IVP (6.1) is defined by reversing the order.
Theorem 7.9.
Assume that assumptions (H27)–(H29) hold. Suppose moreover that
-
(H38) The functions
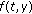 and
and 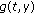 are increasing in
are increasing in 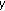 for each
for each 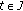 .
. -
(H39)
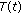 is order-preserving, that is,
is order-preserving, that is, 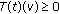 whenever
whenever 
-
(H40) The IVP (6.1) has a lower mild solution
 and an upper mild solution
and an upper mild solution  with
with  .
.
Then IVP (6.1) has a minimal and a maximal mild solutions on  .
.
References
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science, Amsterdam, The Netherlands; 2006:xvi+523.
Kiryakova V: Generalized Fractional Calculus and Applications, Pitman Research Notes in Mathematics Series. Volume 301. Longman Scientific & Technical, Harlow, UK; John Wiley & Sons, New York, NY, USA; 1994:x+388.
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Yverdon, Switzerland; 1993:xxxvi+976.
Agarwal RP, Benchohra M, Hamani S: Boundary value problems for fractional differential equations. to appear in Georgian Mathematical Journal
Diethelm K, Freed AD: On the solution of nonlinear fractional order differential equations used in the modeling of viscoplasticity. In Scientific Computing in Chemical Engineering II: Computational Fluid Dynamics, Reaction Engineering and Molecular Properties. Edited by: Keil F, Mackens W, Voß H, Werther J. Springer, Heidelberg, Germany; 1999:217-224.
Diethelm K, Ford NJ: Analysis of fractional differential equations. Journal of Mathematical Analysis and Applications 2002,265(2):229-248. 10.1006/jmaa.2000.7194
El-Sayed AMA: Fractional order evolution equations. Journal of Fractional Calculus 1995, 7: 89-100.
El-Sayed AMA: Fractional-order diffusion-wave equation. International Journal of Theoretical Physics 1996,35(2):311-322. 10.1007/BF02083817
El-Sayed AMA: Nonlinear functional-differential equations of arbitrary orders. Nonlinear Analysis: Theory, Methods & Applications 1998,33(2):181-186. 10.1016/S0362-546X(97)00525-7
Gaul L, Klein P, Kempfle S: Damping description involving fractional operators. Mechanical Systems and Signal Processing 1991,5(2):81-88. 10.1016/0888-3270(91)90016-X
Glockle WG, Nonnenmacher TF: A fractional calculus approach to self-similar protein dynamics. Biophysical Journal 1995,68(1):46-53. 10.1016/S0006-3495(95)80157-8
Lakshmikantham V, Devi JV: Theory of fractional differential equations in a Banach space. European Journal of Pure and Applied Mathematics 2008,1(1):38-45.
Mainardi F: Fractional calculus: some basic problems in continuum and statistical mechanis. In Fractals and Fractional Calculus in Continuum Mechanics. Edited by: Carpinteri A, Mainard F. Springer, Vienna, Austria; 1997:291-348.
Metzler F, Schick W, Kilian HG, Nonnenmacher TF: Relaxation in filled polymers: a fractional calculus approach. Journal of Chemical Physics 1995,103(16):7180-7186. 10.1063/1.470346
Momani SM, Hadid SB: Some comparison results for integro-fractional differential inequalities. Journal of Fractional Calculus 2003, 24: 37-44.
Momani SM, Hadid SB, Alawenh ZM: Some analytical properties of solutions of differential equations of noninteger order. International Journal of Mathematics and Mathematical Sciences 2004,2004(13–16):697-701.
Podlubny I, Petráš I, Vinagre BM, O'Leary P, Dorčák L': Analogue realizations of fractional-order controllers. Fractional order calculus and its applications. Nonlinear Dynamics 2002,29(1–4):281-296.
Yu C, Gao G: Existence of fractional differential equations. Journal of Mathematical Analysis and Applications 2005,310(1):26-29. 10.1016/j.jmaa.2004.12.015
El-Borai MM: On some fractional evolution equations with nonlocal conditions. International Journal of Pure and Applied Mathematics 2005,24(3):405-413.
El-Borai MM: The fundamental solutions for fractional evolution equations of parabolic type. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(3):197-211. 10.1155/S1048953304311020
Jaradat OK, Al-Omari A, Momani S: Existence of the mild solution for fractional semilinear initial value problems. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):3153-3159. 10.1016/j.na.2007.09.008
Goldstein JA: Semigroups of Linear Operators and Applications, Oxford Mathematical Monographs. Clarendon Press/Oxford University Press, New York, NY, USA; 1985:x+245.
Fattorini HO: Second Order Linear Differential Equations in Banach Spaces, North-Holland Mathematics Studies. Volume 108. North-Holland, Amsterdam, The Netherlands; 1985:xiii+314.
Travis CC, Webb GF: Second order differential equations in Banach spaces. In Nonlinear Equations in Abstract Spaces (Proc. Internat. Sympos., Univ. Texas, Arlington, Tex., 1977). Academic Press, New York, NY, USA; 1978:331-361.
Travis CC, Webb GF: Cosine families and abstract nonlinear second order differential equations. Acta Mathematica Academiae Scientiarum Hungaricae 1978,32(1-2):75-96. 10.1007/BF01902205
Ahmed NU: Semigroup Theory with Applications to Systems and Control, Pitman Research Notes in Mathematics Series. Volume 246. Longman Scientific & Technical, Harlow, UK; John Wiley & Sons, New York, NY, USA; 1991:x+282.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Kisielewicz M: Differential Inclusions and Optimal Control, Mathematics and Its Applications. Volume 44. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1991:xx+240.
Deimling K: Multivalued Differential Equations, de Gruyter Series in Nonlinear Analysis and Applications. Volume 1. Walter de Gruyter, Berlin, Germany; 1992:xii+260.
Górniewicz L: Topological Fixed Point Theory of Multivalued Mappings, Mathematics and Its Applications. Volume 495. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1999:x+399.
Hu S, Papageorgiou NS: Handbook of Multivalued Analysis. Volume I: Theory, Mathematics and Its Applications. Volume 419. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:xvi+964.
Henry D: Geometric Theory of Semilinear Parabolic Partial Differential Equations. Springer, Berlin, Germany; 1989.
Covitz H, Nadler SB Jr.: Multi-valued contraction mappings in generalized metric spaces. Israel Journal of Mathematics 1970,8(1):5-11. 10.1007/BF02771543
Granas A, Dugundji J: Fixed Point Theory, Springer Monographs in Mathematics. Springer, New York, NY, USA; 2003:xvi+690.
Martelli M: A Rothe's type theorem for non-compact acyclic-valued maps. Bollettino della Unione Matematica Italiana. Serie 4 1975,11(3, supplement):70-76.
Burton TA, Kirk C: A fixed point theorem of Krasnoselskii-Schaefer type. Mathematische Nachrichten 1998, 189: 23-31. 10.1002/mana.19981890103
Dhage BC: Multi-valued mappings and fixed points. I. Nonlinear Functional Analysis and Applications 2005,10(3):359-378.
Dhage BC: Multi-valued mappings and fixed points. II. Tamkang Journal of Mathematics 2006,37(1):27-46.
Hale JK, Kato J: Phase space for retarded equations with infinite delay. Funkcialaj Ekvacioj 1978,21(1):11-41.
Hino Y, Murakami S, Naito T: Functional-Differential Equations with Infinite Delay, Lecture Notes in Mathematics. Volume 1473. Springer, Berlin, Germany; 1991:x+317.
Hale JK: Theory of Functional Differential Equations, Applied Mathematical Sciences. Volume 3. 2nd edition. Springer, New York, NY, USA; 1977:x+365.
Hale JK, Verduyn Lunel SM: Introduction to Functional-Differential Equations, Applied Mathematical Sciences. Volume 99. Springer, New York, NY, USA; 1993:x+447.
Kolmanovskii V, Myshkis A: Introduction to the Theory and Applications of Functional-Differential Equations, Mathematics and Its Applications. Volume 463. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1999:xvi+648.
Wu J: Theory and Applications of Partial Functional-Differential Equations, Applied Mathematical Sciences. Volume 119. Springer, New York, NY, USA; 1996.
Belarbi A, Benchohra M, Hamani S, Ntouyas SK: Perturbed functional differential equations with fractional order. Communications in Applied Analysis 2007,11(3-4):429-440.
Belarbi A, Benchohra M, Ouahab A: Uniqueness results for fractional functional differential equations with infinite delay in Fréchet spaces. Applicable Analysis 2006,85(12):1459-1470. 10.1080/00036810601066350
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: Existence results for fractional functional differential inclusions with infinite delay and applications to control theory. Fractional Calculus & Applied Analysis 2008,11(1):35-56.
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: Existence results for fractional order functional differential equations with infinite delay. Journal of Mathematical Analysis and Applications 2008,338(2):1340-1350. 10.1016/j.jmaa.2007.06.021
Belmekki M, Benchohra M: Existence results for fractional order semilinear functional differential equations. Proceedings of A. Razmadze Mathematical Institute 2008, 146: 9-20.
Belmekki M, Benchohra M, Górniewicz L: Functional differential equations with fractional order and infinite delay. Fixed Point Theory 2008,9(2):423-439.
Heymans N, Podlubny I: Physical interpretation of initial conditions for fractional differential equations with Riemann-Liouville fractional derivatives. Rheologica Acta 2006,45(5):765-772. 10.1007/s00397-005-0043-5
Podlubny I: Geometric and physical interpretation of fractional integration and fractional differentiation. Fractional Calculus & Applied Analysis 2002,5(4):367-386.
Prüss J: Evolutionary Integral Equations and Applications, Monographs in Mathematics. Volume 87. Birkhäuser, Basel, Switzerland; 1993:xxvi+366.
Hilfe R (Ed): Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Hernández E, Henríquez HR: Existence results for partial neutral functional differential equations with unbounded delay. Journal of Mathematical Analysis and Applications 1998,221(2):452-475. 10.1006/jmaa.1997.5875
Hernández E, Henríquez HR: Existence of periodic solutions of partial neutral functional differential equations with unbounded delay. Journal of Mathematical Analysis and Applications 1998,221(2):499-522. 10.1006/jmaa.1997.5899
El-Sayed AMA, Ibrahim A-G: Multivalued fractional differential equations. Applied Mathematics and Computation 1995,68(1):15-25. 10.1016/0096-3003(94)00080-N
Ouahab A: Some results for fractional boundary value problem of differential inclusions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3877-3896. 10.1016/j.na.2007.10.021
Agarwal RP, Benchohra M, Hamani S: Boundary value problems for differential inclusions with fractional order. Advanced Studies in Contemporary Mathematics 2008,16(2):181-196.
Chang Y-K, Nieto JJ: Some new existence results for fractional differential inclusions with boundary conditions. Mathematical and Computer Modelling 2009,49(3-4):605-609. 10.1016/j.mcm.2008.03.014
Yosida K: Functional Analysis, Grundlehren der Mathematischen Wissenschaften. Volume 123. 6th edition. Springer, Berlin, Germany; 1980:xii+501.
Castaing C, Valadier M: Convex Analysis and Measurable Multifunctions, Lecture Notes in Mathematics. Volume 580. Springer, Berlin, Germany; 1977:vii+278.
Heikkilä S, Lakshmikantham V: Monotone Iterative Techniques for Discontinuous Nonlinear Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 181. Marcel Dekker, New York, NY, USA; 1994:xii+514.
Joshi MC, Bose RK: Some Topics in Nonlinear Functional Analysis, A Halsted Press Book. John Wiley & Sons, New York, NY, USA; 1985:viii+311.
Dhage BC, Henderson J: Existence theory for nonlinear functional boundary value problems. Electronic Journal of Qualitative Theory of Differential Equations 2004,2004(1):1-15.
Acknowledgment
The authors thank the referees for their comments and remarks.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R., Belmekki, M. & Benchohra, M. A Survey on Semilinear Differential Equations and Inclusions Involving Riemann-Liouville Fractional Derivative. Adv Differ Equ 2009, 981728 (2009). https://doi.org/10.1155/2009/981728
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/981728

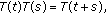 for all
for all 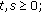
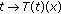 is strongly continuous, for each
is strongly continuous, for each 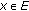 , that is,
, that is,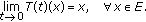
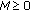 and
and  such that
such that 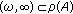 ,
, 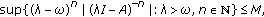 where
where 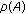 is the resolvent set of
is the resolvent set of 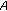 and
and 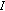 is the identity operator in
is the identity operator in  .
.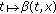 is measurable for each
is measurable for each 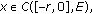
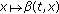 is u.s.c. for almost all
is u.s.c. for almost all 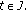
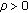 , there exists a function
, there exists a function 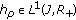 such that
such that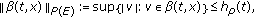
 -Lipschitz if and only if there exists
-Lipschitz if and only if there exists  such that
such that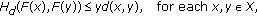
 -Lipschitz with
-Lipschitz with 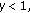
 has a fixed point if there exists
has a fixed point if there exists 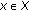 such that
such that 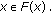
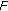 has a fixed point, or
has a fixed point, or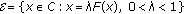 is unbounded.
is unbounded.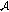 is a contraction;
is a contraction;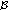 is completely continuous.
is completely continuous.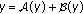 has a solution, or
has a solution, or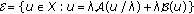 is unbounded for
is unbounded for 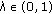 .
.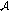 is a contraction;
is a contraction;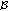 is completely continuous.
is completely continuous.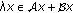 has a solution for
has a solution for 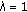 , or
, or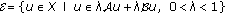 is unbounded.
is unbounded. and functions
and functions 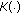 ,
, 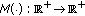 with
with 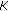 continuous and
continuous and  locally bounded, such that for any
locally bounded, such that for any 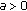 , if
, if  ,
, 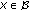 , and
, and 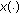 is continuous on
is continuous on 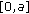 , then for every
, then for every 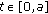 the following conditions hold:
the following conditions hold: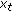 is in
is in 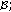
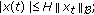
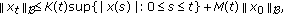 and
and 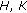 , and
, and  are independent of
are independent of 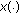 .
.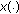 in
in 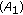 ,
, 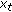 is a
is a  -valued continuous function on
-valued continuous function on 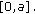
 is complete.
is complete.
 such that
such that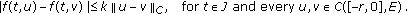
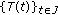 is compact for
is compact for 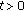 .
. such that
such that
 such that
such that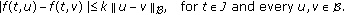
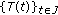 is compact for
is compact for  .
.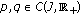 such that
such that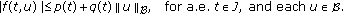
 such that
such that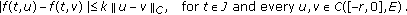
 such that
such that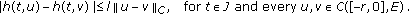
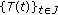 is compact for
is compact for  .
. such that
such that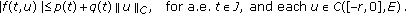
 is continuous and completely continuous, and for every bounded set
is continuous and completely continuous, and for every bounded set  , the set
, the set  is equicontinuous in
is equicontinuous in 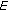 .
.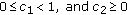 such that
such that
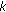 such that
such that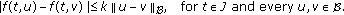
 such that
such that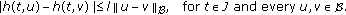
 is compact for
is compact for  .
. such that
such that
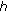 is continuous and completely continuous, and for every bounded set
is continuous and completely continuous, and for every bounded set  , the set
, the set 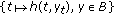 is equicontinuous in
is equicontinuous in 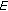 .
. such that
such that
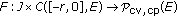 is Carathéodory.
is Carathéodory.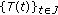 is compact for
is compact for 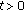 .
.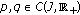 such that
such that
 is Carathéodory.
is Carathéodory.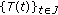 is compact for
is compact for 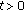 .
. such that
such that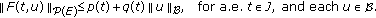
 such that
such that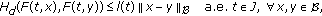
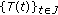 is compact for
is compact for 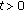 .
. such that
such that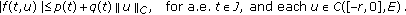
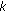 such that
such that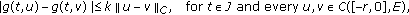
 is compact for
is compact for  .
.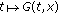 is measurable, convex valued and integrably bounded for each
is measurable, convex valued and integrably bounded for each  .
. such that
such that
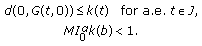
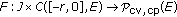 is Carathéodory.
is Carathéodory.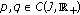 such that
such that
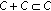 ,
, for
for 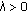 ,
,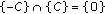 .
. is increasing in
is increasing in  for each
for each 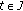 .
.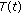 is order-preserving, that is,
is order-preserving, that is, 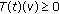 whenever
whenever 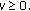
 and an upper mild solution
and an upper mild solution  with
with 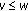 .
.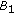 is a contraction,
is a contraction,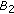 is completely continuous,
is completely continuous, and
and 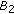 are strictly monotone increasing,
are strictly monotone increasing,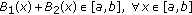 .
.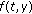 and
and 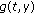 are increasing in
are increasing in 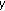 for each
for each 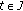 .
.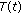 is order-preserving, that is,
is order-preserving, that is, 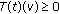 whenever
whenever 
 and an upper mild solution
and an upper mild solution  with
with  .
.