- Research Article
- Open access
- Published:
A Functional Inequality in Restricted Domains of Banach Modules
Advances in Difference Equations volume 2009, Article number: 973709 (2009)
Abstract
We investigate the stability problem for the following functional inequality  on restricted domains of Banach modules over a
on restricted domains of Banach modules over a  -algebra. As an application we study the asymptotic behavior of a generalized additive mapping.
-algebra. As an application we study the asymptotic behavior of a generalized additive mapping.
1. Introduction and Preliminaries
The following question concerning the stability of group homomorphisms was posed by Ulam [1]: Under what conditions does there exist a group homomorphism near an approximate group homomorphism?
Hyers [2] considered the case of approximately additive mappings  , where
, where  and
and  are Banach spaces and
are Banach spaces and  satisfiesHyers inequality
satisfiesHyers inequality

for all  .
.
In 1950, Aoki [3] provided a generalization of the Hyers' theorem for additive mappings and in 1978, Rassias [4] generalized the Hyers' theorem for linear mappings by allowing the Cauchy difference to be unbounded (see also [5]). The result of Rassias' theorem has been generalized by Forti [6, 7] and G vruta [8] who permitted the Cauchy difference to be bounded by a general control function. During the last three decades a number of papers have been published on the generalized Hyers-Ulam stability to a number of functional equations and mappings (see [9–23]). We also refer the readers to the books [24–28].
vruta [8] who permitted the Cauchy difference to be bounded by a general control function. During the last three decades a number of papers have been published on the generalized Hyers-Ulam stability to a number of functional equations and mappings (see [9–23]). We also refer the readers to the books [24–28].
Throughout this paper, let  be a unital
be a unital  -algebra with unitary group
-algebra with unitary group  , unit
, unit  and norm
and norm  . Assume that
. Assume that  is a left
is a left  -module and
-module and  is a left Banach
is a left Banach  -module. An additive mapping
-module. An additive mapping  is called
is called  -linear if
-linear if  for all
for all  and all
and all  . In this paper, we investigate the stability problem for the following functional inequality:
. In this paper, we investigate the stability problem for the following functional inequality:

on restricted domains of Banach modules over a  -algebra, where
-algebra, where  are nonzero positive real numbers. As an application we study the asymptotic behavior of a generalized additive mapping.
are nonzero positive real numbers. As an application we study the asymptotic behavior of a generalized additive mapping.
2. Solutions of the Functional Inequality (1.2)
Theorem 2.1.
Let  and
and  be left
be left  -modules and let
-modules and let  be nonzero real numbers. If a mapping
be nonzero real numbers. If a mapping  with
with  satisfies the functional inequality
satisfies the functional inequality

for all  and all
and all  , then
, then  is
is  -linear.
-linear.
Proof.
Letting  in (2.1)
in (2.1) we get
we get

for all  and all
and all  . Letting
. Letting  (resp.,
(resp.,  ) in (2.2), we get
) in (2.2), we get

for all  and all
and all  . Hence
. Hence  and it follows from (2.2) and (2.3) that and
and it follows from (2.2) and (2.3) that and  for all
for all  and all
and all  Therefore
Therefore  for all
for all  Hence
Hence  for all
for all  and all rational numbers
and all rational numbers  .
.
Now let  and let
and let  be an integer number with
be an integer number with  . Then by Theorem 1 of [29], there exist elements
. Then by Theorem 1 of [29], there exist elements  such that
such that  . Since
. Since  is additive and
is additive and  for all
for all  all rational numbers
all rational numbers  and all
and all  , we have
, we have

for all  . Replacing
. Replacing  instead of
instead of  in the above equation, we have
in the above equation, we have

for all  Since
Since  is an arbitrary nonzero element in
is an arbitrary nonzero element in  in the previous paragraph, one can replace
in the previous paragraph, one can replace  instead of
instead of  in (2.5). Thus we have
in (2.5). Thus we have  for all
for all  and all
and all  So
So  is
is  -linear.
-linear.
The following theorem is another version of Theorem 2.1 on a restricted domain when 
Theorem 2.2.
Let  and
and  be left
be left  -modules and let
-modules and let  be nonzero positive real numbers. Assume that a mapping
be nonzero positive real numbers. Assume that a mapping  satisfies
satisfies  and the functional inequality (2.1) for all
and the functional inequality (2.1) for all  with
with  and all
and all  . Then
. Then  is
is  -linear.
-linear.
Proof.
Letting  with
with  in (2.1), we get
in (2.1), we get

for all  . Let
. Let  and let
and let  Then
Then

Therefore replacing  and
and  by
by  and
and  in (2.6), respectively, we get
in (2.6), respectively, we get

for all  with
with  and all
and all  .
.
Similar to the proof of Theorem 3 of [30] (see also [31]), we prove that  satisfies (2.8) for all
satisfies (2.8) for all  and all
and all  . Suppose
. Suppose  If
If  , let
, let  with
with  otherwise
otherwise

Since  it is easy to verify that
it is easy to verify that

Therefore

Hence  satisfies (2.8) and we infer that
satisfies (2.8) and we infer that  satisfies (2.2) for all
satisfies (2.2) for all  and all
and all  . By Theorem 2.1,
. By Theorem 2.1,  is
is  -linear.
-linear.
3. Generalized Hyers-Ulam Stability of (1.2) on a Restricted Domain
In this section, we investigate the stability problem for  -linear mappings associated to the functional inequality (1.2) on a restricted domain. For convenience, we use the following abbreviation for a given function
-linear mappings associated to the functional inequality (1.2) on a restricted domain. For convenience, we use the following abbreviation for a given function  and
and 

for all 
Theorem 3.1.
Let  and
and  be given. Assume that a mapping
be given. Assume that a mapping  satisfies the functional inequality
satisfies the functional inequality

for all  with
with  and all
and all  . Then there exist a unique
. Then there exist a unique  -linear mapping
-linear mapping  and a constant
and a constant  such that
such that

for all 
Proof.
Let  with
with  . Then (3.2) implies that
. Then (3.2) implies that

Thus

for all  with
with  and all
and all  . Let
. Let  and let
and let  Then
Then  Therefore it follows from (3.5) that
Therefore it follows from (3.5) that

for all  with
with  and all
and all  . For the case
. For the case  let
let  be an element of
be an element of  which is defined in the proof of Theorem 2.2. It is clear that
which is defined in the proof of Theorem 2.2. It is clear that  Using (2.11) and (3.6), we get
Using (2.11) and (3.6), we get

for all  with
with  and all
and all  . Hence
. Hence

for all  and all
and all  , where
, where

Letting  and
and  in (3.8), respectively, we get
in (3.8), respectively, we get

for all  and all
and all  . It follows from (3.8) and (3.10) that
. It follows from (3.8) and (3.10) that

for all  . By the results of Hyers [2] and Rassias [4], there exists a unique additive mapping
. By the results of Hyers [2] and Rassias [4], there exists a unique additive mapping  given by
given by  such that
such that

for all  . It follows from the definition of
. It follows from the definition of  and (3.2) that
and (3.2) that  and
and  for all
for all  with
with  and all
and all  . Hence
. Hence  is
is  -linear by Theorem 2.2.
-linear by Theorem 2.2.
We apply the result of Theorem 3.1 to study the asymptotic behavior of a generalized additive mapping. An asymptotic property of additive mappings has been proved by Skof [32] (see also [30, 33]).
Corollary 3.2.
Let  be nonzero positive real numbers. Assume that a mapping
be nonzero positive real numbers. Assume that a mapping  with
with  satisfies
satisfies

for all  then
then  is
is  -linear.
-linear.
Proof.
It follows from (3.13) that there exists a sequence  monotonically decreasing to zero, such that
monotonically decreasing to zero, such that

for all  with
with  and all
and all  . Therefore
. Therefore

for all  with
with  and all
and all  . Applying (3.15) and Theorem 3.1, we obtain a sequence
. Applying (3.15) and Theorem 3.1, we obtain a sequence  of unique
of unique  -linear mappings satisfying
-linear mappings satisfying

for all  . Since the sequence
. Since the sequence  is monotonically decreasing, we conclude
is monotonically decreasing, we conclude

for all  and all
and all  The uniqueness of
The uniqueness of  implies
implies  for all
for all  Hence letting
Hence letting  in (3.16), we obtain that
in (3.16), we obtain that  is
is  -linear.
-linear.
The following theorem is another version of Theorem 3.1 for the case 
Theorem 3.3.
Let  be given and let
be given and let  be nonzero real numbers. Assume that a mapping
be nonzero real numbers. Assume that a mapping  with
with  satisfies the functional inequality
satisfies the functional inequality

for all  with
with  and all
and all  . Then there exists a unique
. Then there exists a unique  -linear mapping
-linear mapping  such that
such that

for all  with
with  and
and  .
.
Proof.
Letting  in (3.18), we get
in (3.18), we get

for all  with
with  and all
and all  . Hence
. Hence

for all  with
with  and all
and all  . It follows from (3.21) that
. It follows from (3.21) that

for all  with
with  and all
and all  . Adding (3.21) to (3.22), we get
. Adding (3.21) to (3.22), we get

for all  with
with  and all
and all  . Therefore
. Therefore

for all  with
with  . Let
. Let  with
with  . We may put
. We may put  in (3.24) to obtain
in (3.24) to obtain

We can replace  by
by  in (3.25) for all nonnegative integers
in (3.25) for all nonnegative integers  Then using a similar argument given in [4], we have
Then using a similar argument given in [4], we have

Hence we have the following inequality:

for all  with
with  and all integers
and all integers  Since
Since  is complete, (3.27) shows that the limit
is complete, (3.27) shows that the limit  exists for all
exists for all  with
with  . Letting
. Letting  and
and  in (3.27), we obtain that
in (3.27), we obtain that  satisfies inequality (3.19) for all
satisfies inequality (3.19) for all  with
with  . It follows from the definition of
. It follows from the definition of  and (3.24) that
and (3.24) that

for all  with
with  . Hence
. Hence

for all  with
with  . We extend the additivity of
. We extend the additivity of  to the whole space
to the whole space  by using an extension method of Skof [34]. Let
by using an extension method of Skof [34]. Let  and
and  be given with
be given with  Let
Let  be the smallest integer such that
be the smallest integer such that  We define the mapping
We define the mapping  by
by

Let  be given with
be given with  and let
and let  be the smallest integer such that
be the smallest integer such that  Then
Then  is the smallest integer satisfying
is the smallest integer satisfying  If
If  , we have
, we have  and
and  . Therefore
. Therefore  For the case
For the case  , it follows from the definition of
, it follows from the definition of  that
that

From the definition of  and (3.29), we get that
and (3.29), we get that  holds true for all
holds true for all  Let
Let  and let
and let  be an integer such that
be an integer such that  Then
Then

It remains to prove that  is
is  -linear. Let
-linear. Let  and let
and let  be a positive integer such that
be a positive integer such that  Since
Since  for all
for all  and
and  satisfies (3.28), we have
satisfies (3.28), we have

Hence  is additive. Since
is additive. Since  for all
for all  , we have from (3.22) that
, we have from (3.22) that  for all
for all  and all
and all  Letting
Letting  , we get
, we get  . Therefore
. Therefore  for all
for all  and all
and all  This proves that
This proves that  is
is  -linear. Also,
-linear. Also,  satisfies inequality (3.19) for all
satisfies inequality (3.19) for all  with
with  , by the definition of
, by the definition of  .
.
For the case  we use the Gajda's example [35] to give the following counterexample.
we use the Gajda's example [35] to give the following counterexample.
Example 3.4.
Let  be defined by
be defined by

Consider the function  by the formula
by the formula

It is clear that  is continuous, bounded by
is continuous, bounded by  on
on  and
and

for all  (see [35]). It follows from (3.36) that the following inequality:
(see [35]). It follows from (3.36) that the following inequality:

holds for all  First we show that
First we show that

for all  If
If  satisfies (3.38) for all
satisfies (3.38) for all  then
then  satisfies (3.38) for all
satisfies (3.38) for all  To see this, let
To see this, let  (the result is obvious when
(the result is obvious when  ). Then
). Then  for all
for all  Replacing
Replacing  by
by  , we get that
, we get that  for all
for all  Hence we may assume that
Hence we may assume that  If
If  or
or  then
then

Now suppose that  Then there exists an integer
Then there exists an integer  such that
such that

Therefore

Hence

for all  From the definition of
From the definition of  and (3.40), we have
and (3.40), we have

Therefore  satisfies (3.38). Now we prove that
satisfies (3.38). Now we prove that

for all  and all
and all  where
where

It follows from (3.37) and (3.38) that

for all  and all
and all  Thus
Thus  satisfies inequality (3.18) for
satisfies inequality (3.18) for  Let
Let  be a linear functional such that
be a linear functional such that

for all  where
where  is a positive constant. Then there exists a constant
is a positive constant. Then there exists a constant  such that
such that  for all rational numbers
for all rational numbers  . So we have
. So we have

for all rational numbers  . Let
. Let  with
with  If
If  , then
, then  for all
for all  So
So

which contradicts (3.48).
References
Ulam SM: A Collection of the Mathematical Problems. Interscience, New York, NY, USA; 1960.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences 1941, 27: 222-224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64-66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978, 72: 297-300. 10.1090/S0002-9939-1978-0507327-1
Bourgin DG: Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society 1951, 57: 223-237. 10.1090/S0002-9904-1951-09511-7
Forti GL: An existence and stability theorem for a class of functional equations. Stochastica 1980, 4: 23-30. 10.1080/17442508008833155
Forti GL: Hyers-Ulam stability of functional equations in several variables. Aequationes Mathematicae 1995,50(1-2):143-190. 10.1007/BF01831117
Gavruta P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431-436. 10.1006/jmaa.1994.1211
Cholewa PW: Remarks on the stability of functional equations. Aequationes Mathematicae 1984,27(1):76-86. 10.1007/BF02192660
Czerwik S: On the stability of the quadratic mapping in normed spaces. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1992,62(1):59-64. 10.1007/BF02941618
Faiziev VA, Rassias ThM, Sahoo PK:The space of
 -additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455-4472. 10.1090/S0002-9947-02-03036-2
-additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455-4472. 10.1090/S0002-9947-02-03036-2Grabiec A: The generalized Hyers-Ulam stability of a class of functional equations. Publicationes Mathematicae Debrecen 1996,48(3-4):217-235.
Hyers DH, Rassias ThM: Approximate homomorphisms. Aequationes Mathematicae 1992,44(2-3):125-153. 10.1007/BF01830975
Isac G, Rassias ThM:Stability of
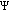 -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19: 219-228. 10.1155/S0161171296000324
-additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19: 219-228. 10.1155/S0161171296000324Jun K-W, Lee Y-H: On the Hyers-Ulam-Rassias stability of a pexiderized quadratic inequality. Mathematical Inequalities and Applications 2001,4(1):93-118.
Kannappan Pl: Quadratic functional equation and inner product spaces. Results in Mathematics 1995, 27: 368-372.
Najati A: Hyers-Ulam stability of an n-apollonius type quadratic mapping. Bulletin of the Belgian Mathematical Society—Simon Stevin 2007,14(4):755-774.
Najati A, Park C: Hyers-Ulam-Rassias stability of homomorphisms in quasi-Banach algebras associated to the Pexiderized Cauchy functional equation. Journal of Mathematical Analysis and Applications 2007,335(2):763-778. 10.1016/j.jmaa.2007.02.009
Najati A, Park C:The Pexiderized Apollonius-Jensen type additive mapping and isomorphisms between
 -algebras. Journal of Difference Equations and Applications 2008,14(5):459-479. 10.1080/10236190701466546
-algebras. Journal of Difference Equations and Applications 2008,14(5):459-479. 10.1080/10236190701466546Park C-G: On the stability of the linear mapping in Banach modules. Journal of Mathematical Analysis and Applications 2002,275(2):711-720. 10.1016/S0022-247X(02)00386-4
Rassias ThM: On a modified Hyers-Ulam sequence. Journal of Mathematical Analysis and Applications 1991,158(1):106-113. 10.1016/0022-247X(91)90270-A
Rassias ThM: On the stability of functional equations and a problem of Ulam. Acta Applicandae Mathematicae 2000, 62: 23-130. 10.1023/A:1006499223572
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000,251(1):264-284. 10.1006/jmaa.2000.7046
Aczél J, Dhombres J: Functional Equations in Several Variables. Cambridge University Press, Cambridge, UK; 1989.
Czerwik S: Functional Equations and Inequalities in Several Variables. World Scientific, River Edge, NJ, USA; 2002.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables. Birkhäuser, Basel, Switzerland; 1998.
Jung S: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001.
Rassias ThM: Functional Equations, Inequalities and Applications. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003.
Kadison RV, Pedersen G: Means and convex combinations of unitary operators. Mathematica Scandinavica 1985, 57: 249-266.
Jung S-MO: Hyers-ulam-rassias stability of jensen's equation and its application. Proceedings of the American Mathematical Society 1998,126(11):3137-3143. 10.1090/S0002-9939-98-04680-2
Jung S, Moslehian MS, Sahoo PK: Stability of a generalized Jensen equation on restricted domains. http://arxiv.org/abs/math/0511320v1
Skof F:Sull' approssimazione delle applicazioni localmente
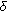 -additive. Atti della Accademia delle Scienze di Torino 1983, 117: 377-389.
-additive. Atti della Accademia delle Scienze di Torino 1983, 117: 377-389.Hyers DH, Isac G, Rassias ThM: On the asymptoticity aspect of Hyers-Ulam stability of mappings. Proceedings of the American Mathematical Society 1998,126(2):425-430. 10.1090/S0002-9939-98-04060-X
Skof F: On the stability of functional equations on a restricted domain and a related topic. In Stabiliy of Mappings of Hyers-Ulam Type. Edited by: Rassias ThM, Tabor J. Hadronic Press, Palm Harbor, Fla, USA; 1994:41-151.
Gajda Z: On stability of additive mappings. International Journal of Mathematics and Mathematical Sciences 1991, 14: 431-434. 10.1155/S016117129100056X
Acknowledgments
The third author was supported by Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (NRF-2009-0070788). The authors would like to thank the referees for a number of valuable suggestions regarding a previous version of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Moghimi, M.B., Najati, A. & Park, C. A Functional Inequality in Restricted Domains of Banach Modules. Adv Differ Equ 2009, 973709 (2009). https://doi.org/10.1155/2009/973709
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/973709
 -additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455-4472. 10.1090/S0002-9947-02-03036-2
-additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455-4472. 10.1090/S0002-9947-02-03036-2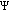 -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19: 219-228. 10.1155/S0161171296000324
-additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19: 219-228. 10.1155/S0161171296000324 -algebras. Journal of Difference Equations and Applications 2008,14(5):459-479. 10.1080/10236190701466546
-algebras. Journal of Difference Equations and Applications 2008,14(5):459-479. 10.1080/10236190701466546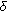 -additive. Atti della Accademia delle Scienze di Torino 1983, 117: 377-389.
-additive. Atti della Accademia delle Scienze di Torino 1983, 117: 377-389.