- Research Article
- Open access
- Published:
A Note on the 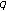 -Euler Measures
-Euler Measures
Advances in Difference Equations volume 2009, Article number: 956910 (2009)
Abstract
Properties of  -extensions of Euler numbers and polynomials which generalize those satisfied by
-extensions of Euler numbers and polynomials which generalize those satisfied by  and
and  are used to construct
are used to construct  -extensions of
-extensions of  -adic Euler measures and define
-adic Euler measures and define  -adic
-adic  -
- -series which interpolate
-series which interpolate  -Euler numbers at negative integers. Finally, we give Kummer Congruence for the
-Euler numbers at negative integers. Finally, we give Kummer Congruence for the  -extension of ordinary Euler numbers.
-extension of ordinary Euler numbers.
1. Introduction
Let  be a fixed prime number. Throughout this paper
be a fixed prime number. Throughout this paper  and
and  will, respectively, denote the ring of
will, respectively, denote the ring of  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers, the complex number field, and the completion of algebraic closure of
-adic rational numbers, the complex number field, and the completion of algebraic closure of  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  . When one talks of
. When one talks of  -extension,
-extension,  is variously considered as an indeterminate, a complex number
is variously considered as an indeterminate, a complex number  or
or  -adic numbers
-adic numbers  . If
. If  , one normally assumes
, one normally assumes  . If
. If  , one normally assumes
, one normally assumes  . In this paper, we use the notations of
. In this paper, we use the notations of  -number as follows (see [1–37]):
-number as follows (see [1–37]):

The ordinary Euler numbers are defined as (see [1–37])

where  is written as
is written as  when
when  is replaced by
is replaced by  . From the definition of Euler number, we can derive
. From the definition of Euler number, we can derive

with the usual convention of replacing  by
by 
Remark 1.1.
The second kind Euler numbers are also defined as follows (see [25]):

The Euler polynomials are also defined by

Thus, we have

In [7],  -Euler numbers,
-Euler numbers,  , can be determined inductively by
, can be determined inductively by

where  must be replaced by
must be replaced by  , symbolically. The
, symbolically. The  -Euler polynomials
-Euler polynomials  are given by
are given by  that is,
that is,

Let  be a fixedoddpositive integer. Then we have (see [7])
be a fixedoddpositive integer. Then we have (see [7])

We use (1.9) to get bounded  -adic
-adic  -Euler measures and finally take the Mellin transform to define
-Euler measures and finally take the Mellin transform to define  -adic
-adic  -
- -series which interpolate
-series which interpolate  -Euler numbers at negative integers.
-Euler numbers at negative integers.
2.  -adic
-adic  -Euler Measures
-Euler Measures
Let  be a fixed odd positive integer, and let
be a fixed odd positive integer, and let  be a fixed odd prime number. Define
be a fixed odd prime number. Define

Theorem 2.1.
Let  be given by
be given by

Then  extends to a
extends to a  -valued measure on the compact open sets
-valued measure on the compact open sets  . Note that
. Note that  , where
, where  is fermionic measure on
is fermionic measure on  (see [7])
(see [7])
Proof.
It is sufficient to show that

By (1.9) and (2.2), we see that

and we easily see that  for some constant
for some constant  .
.
Let  be a Dirichlet character with conductor
be a Dirichlet character with conductor  with
with  . Then we define the generalized
. Then we define the generalized  -Euler numbers attached to
-Euler numbers attached to  as follows:
as follows:

The locally constant function  on
on  can be integrated by the
can be integrated by the  -adic bounded
-adic bounded  -Euler measure
-Euler measure  as follows:
as follows:

Therefore, we obtain the following theorem.
Theorem 2.2.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  with
with  . Then one has
. Then one has

Let  . From (2.2), we note that
. From (2.2), we note that

Thus, we have

Therefore, we obtain the following theorem and corollary.
Theorem 2.3.
For  , one has
, one has

Corollary 2.4.
For  , one has
, one has

3. 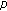 -adic
-adic 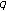 -
-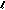 -Series
-Series
In this section, we assume that  with
with  . Let
. Let  denote the Teichmüller character
denote the Teichmüller character  . For
. For  , we set
, we set  . Note that
. Note that  , and
, and  is defined by
is defined by  , for
, for  . For
. For  ,we define
,we define

Thus, we have

Since  for
for  , we have
, we have  Let
Let  . Then we have
. Then we have

Therefore, we obtain the following theorem.
Theorem 3.1.
Let  . Then one has
. Then one has

References
Cenkci M:The
 -adic generalized twisted
-adic generalized twisted  -Euler-
-Euler- -function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37-47.
-function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37-47.Cenkci M, Simsek Y, Kurt V:Further remarks on multiple
 -adic
-adic 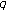 -
-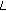 -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.Cenkci M, Can M, Kurt V:
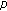 -adic interpolation functions and Kummer-type congruences for
-adic interpolation functions and Kummer-type congruences for 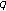 -twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216.
-twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216.Kim T:
 -extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275-278. 10.1134/S1061920807030041
-extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275-278. 10.1134/S1061920807030041Kim T:On the multiple
 -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055Rim S-H, Kim T:A note on
 -adic Euler measure on
-adic Euler measure on 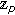 . Russian Journal of Mathematical Physics 2006,13(3):358-361. 10.1134/S1061920806030113
. Russian Journal of Mathematical Physics 2006,13(3):358-361. 10.1134/S1061920806030113Kim T:
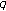 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 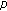 -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3Leyendekkers JV, Shannon AG, Wong CK: Integer structure analysis of the product of adjacent integers and Euler's extension of Fermat's last theorem. Advanced Studies in Contemporary Mathematics 2008,17(2):221-229.
Ozden H, Cangul IN, Simsek Y:Remarks on sum of products of
 -twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.
-twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.Srivastava HM, Kim T, Simsek Y:
 -Bernoulli numbers and polynomials associated with multiple
-Bernoulli numbers and polynomials associated with multiple  -zeta functions and basic
-zeta functions and basic  -series. Russian Journal of Mathematical Physics 2005,12(2):241-268.
-series. Russian Journal of Mathematical Physics 2005,12(2):241-268.Kim T:Note on
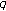 -Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15.
-Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15.Kim T:The modified
 -Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170.
-Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170.Kim T:On a
 -analogue of the
-analogue of the  -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373Kim T:
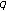 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.Kim T:
 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.Kim T, Choi JY, Sug JY:Extended
 -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic  -adic
-adic  -integral on
-integral on 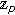 . Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045
. Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045Kim T:On the von Staudt-Clausen's Theorem for the
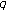 -Euler numbers. Russian Journal of Mathematical Physics 2009.,16(3):
-Euler numbers. Russian Journal of Mathematical Physics 2009.,16(3):Kim T:
 -generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293-298. 10.1134/S1061920806030058
-generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293-298. 10.1134/S1061920806030058Kim T:Multiple
 -adic
-adic 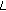 -function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038Kim T:Power series and asymptotic series associated with the
 -analog of the two-variable
-analog of the two-variable  -adic
-adic  -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196.Kim T:Analytic continuation of multiple
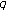 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.Kim T: On Euler-Barnes multiple zeta functions. Russian Journal of Mathematical Physics 2003,10(3):261-267.
Kim T:Symmetry
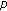 -adic invariant integral on
-adic invariant integral on  for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220
for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220Kim T:Non-Archimedean
 -integrals associated with multiple Changhee
-integrals associated with multiple Changhee  -Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98.
-Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98.Kim T: Euler numbers and polynomials associated with zeta functions. Abstract and Applied Analysis 2008, 2008:-11.
Kim T, Kim Y-H, Hwang K-W:On the
 -extensions of the Bernoulli and Euler numbers, related identities and Lerch zeta function. Proceedings of the Jangjeon Mathematical Society 2009, 12: 1-16.
-extensions of the Bernoulli and Euler numbers, related identities and Lerch zeta function. Proceedings of the Jangjeon Mathematical Society 2009, 12: 1-16.Schork M:Ward's "calculus of sequences",
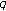 -calculus and the limit
-calculus and the limit 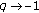 . Advanced Studies in Contemporary Mathematics 2006,13(2):131-141.
. Advanced Studies in Contemporary Mathematics 2006,13(2):131-141.Simsek Y:Theorems on twisted
 -function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205-218.
-function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205-218.Simsek Y: Generating functions of the twisted Bernoulli numbers and polynomials associated with their interpolation functions. Advanced Studies in Contemporary Mathematics 2008,16(2):251-278.
Zhang Z, Yang H: Some closed formulas for generalized Bernoulli-Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society 2008,11(2):191-198.
Simsek Y, Yurekli O, Kurt V: On interpolation functions of the twisted generalized Frobenius-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):187-194.
Simsek Y:On
 -adic twisted
-adic twisted 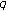 -
-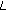 -functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340-348. 10.1134/S1061920806030095
-functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340-348. 10.1134/S1061920806030095Ozden H, Simsek Y, Rim S-H, Cangul IN:A note on
 -adic
-adic 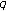 -Euler measure. Advanced Studies in Contemporary Mathematics 2007,14(2):233-239.
-Euler measure. Advanced Studies in Contemporary Mathematics 2007,14(2):233-239.Ozden H, Cangul IN, Simsek Y:Multivariate interpolation functions of higher-order
 -Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.
-Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.Tuenter HJH: A symmetry of power sum polynomials and Bernoulli numbers. The American Mathematical Monthly 2001,108(3):258-261. 10.2307/2695389
Cenkci M, Simsek Y, Kurt V:Multiple two-variable
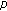 -adic
-adic 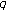 -
- -function and its behavior at
-function and its behavior at  . Russian Journal of Mathematical Physics 2008,15(4):447-459. 10.1134/S106192080804002X
. Russian Journal of Mathematical Physics 2008,15(4):447-459. 10.1134/S106192080804002XAtanassov KT, Vassilev-Missana MV: On one of Murthy-Ashbacher's conjectures related to Euler's totient function. Proceedings of the Jangjeon Mathematical Society 2006,9(1):47-49.
Acknowledgments
This paper was supported by Jangjeon Mathematical Society.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, T., Hwang, KW. & Lee, B. A Note on the 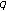 -Euler Measures.
Adv Differ Equ 2009, 956910 (2009). https://doi.org/10.1155/2009/956910
-Euler Measures.
Adv Differ Equ 2009, 956910 (2009). https://doi.org/10.1155/2009/956910
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/956910
 -adic
-adic  -Euler Measures
-Euler Measures lies in
lies in  , (see [
, (see [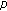 -adic
-adic 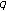 -
-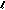 -Series
-Series -adic generalized twisted
-adic generalized twisted  -Euler-
-Euler- -function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37-47.
-function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37-47. -adic
-adic 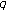 -
-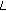 -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68. -adic interpolation functions and Kummer-type congruences for
-adic interpolation functions and Kummer-type congruences for 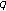 -twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216.
-twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216. -extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275-278. 10.1134/S1061920807030041
-extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275-278. 10.1134/S1061920807030041 -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055 -adic Euler measure on
-adic Euler measure on 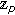 . Russian Journal of Mathematical Physics 2006,13(3):358-361. 10.1134/S1061920806030113
. Russian Journal of Mathematical Physics 2006,13(3):358-361. 10.1134/S1061920806030113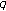 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 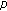 -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3 -twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.
-twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8. -Bernoulli numbers and polynomials associated with multiple
-Bernoulli numbers and polynomials associated with multiple  -zeta functions and basic
-zeta functions and basic  -series. Russian Journal of Mathematical Physics 2005,12(2):241-268.
-series. Russian Journal of Mathematical Physics 2005,12(2):241-268.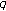 -Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15.
-Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15. -Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170.
-Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170. -analogue of the
-analogue of the  -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373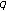 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299. -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57. -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic  -adic
-adic  -integral on
-integral on 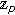 . Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045
. Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045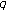 -Euler numbers. Russian Journal of Mathematical Physics 2009.,16(3):
-Euler numbers. Russian Journal of Mathematical Physics 2009.,16(3): -generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293-298. 10.1134/S1061920806030058
-generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293-298. 10.1134/S1061920806030058 -adic
-adic 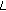 -function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038 -analog of the two-variable
-analog of the two-variable  -adic
-adic  -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196.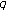 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.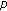 -adic invariant integral on
-adic invariant integral on  for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220
for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220 -integrals associated with multiple Changhee
-integrals associated with multiple Changhee  -Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98.
-Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98. -extensions of the Bernoulli and Euler numbers, related identities and Lerch zeta function. Proceedings of the Jangjeon Mathematical Society 2009, 12: 1-16.
-extensions of the Bernoulli and Euler numbers, related identities and Lerch zeta function. Proceedings of the Jangjeon Mathematical Society 2009, 12: 1-16.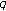 -calculus and the limit
-calculus and the limit  . Advanced Studies in Contemporary Mathematics 2006,13(2):131-141.
. Advanced Studies in Contemporary Mathematics 2006,13(2):131-141. -function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205-218.
-function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205-218. -adic twisted
-adic twisted  -
- -functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340-348. 10.1134/S1061920806030095
-functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340-348. 10.1134/S1061920806030095 -adic
-adic  -Euler measure. Advanced Studies in Contemporary Mathematics 2007,14(2):233-239.
-Euler measure. Advanced Studies in Contemporary Mathematics 2007,14(2):233-239. -Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.
-Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.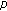 -adic
-adic 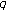 -
- -function and its behavior at
-function and its behavior at  . Russian Journal of Mathematical Physics 2008,15(4):447-459. 10.1134/S106192080804002X
. Russian Journal of Mathematical Physics 2008,15(4):447-459. 10.1134/S106192080804002X