- Research Article
- Open access
- Published:
Existence of Positive Solutions in Generalized Boundary Value Problem for  -Laplacian Dynamic Equations on Time Scales
-Laplacian Dynamic Equations on Time Scales
Advances in Difference Equations volume 2009, Article number: 848191 (2009)
Abstract
We analytically establish the conditions for the existence of at least two or three positive solutions in the generalized  -point boundary value problem for the
-point boundary value problem for the  -Laplacian dynamic equations on time scales by means of the Avery-Henderson fixed point theorem and the five functionals fixed point theorem. Furthermore, we illustrate the possible application of our analytical results with a concrete and nontrivial dynamic equation on specific time scales.
-Laplacian dynamic equations on time scales by means of the Avery-Henderson fixed point theorem and the five functionals fixed point theorem. Furthermore, we illustrate the possible application of our analytical results with a concrete and nontrivial dynamic equation on specific time scales.
1. Introduction
Since the seminal work by Stefan Hilger in 1988, there has been a rapid development in the research of dynamic equations on time scales. The gradually maturing theory of dynamic equations not only includes the majority of the existing analytical results on both differential equations and difference equations with uniform time-steps but also establishes a solid foundation for the research of hybrid equations on different kinds of time scales. More importantly, with this foundation and those ongoing investigations, concrete applications of dynamic equations on time scales in mathematical modeling of real processes and phenomena, such as population dynamics, economic evolutions, chemical kinetics, and neural signal processing, have been becoming fruitful [1–8].
Recently, among the topics in the research of dynamic equations on time scales, the investigation of the boundary value problems for some specific dynamic equations on time scales has become a focal one that attained a great deal of attention from many mathematicians. In fact, systematic framework has been established for the study of the positive solutions in the boundary value problems for the second-order equations on time scales [9–15]. In particular, some results have been analytically obtained on the existence of positive solutions in some specific boundary value problems for the  -Laplacian dynamic equations on time scales [16–19].
-Laplacian dynamic equations on time scales [16–19].
More specifically, He and Li [19], investigated the existence of at least triple positive solutions to the following  -Laplacian boundary value problem:
-Laplacian boundary value problem:

Here and throughout,  is supposed to be a time scale, that is,
is supposed to be a time scale, that is,  is any nonempty closed subset of real numbers in
is any nonempty closed subset of real numbers in  with order and topological structure defined in a canonical way. The closed interval in
with order and topological structure defined in a canonical way. The closed interval in  is defined as
is defined as  . Accordingly, the open interval and the half-open interval could be defined, respectively. In addition, it is assumed that
. Accordingly, the open interval and the half-open interval could be defined, respectively. In addition, it is assumed that  ,
,  ,
,  ,
,  , and
, and  for some positive constants
for some positive constants  and
and  . Moreover,
. Moreover,  is supposed to be the
is supposed to be the  -Laplacian operator, that is,
-Laplacian operator, that is,  and
and  , in which
, in which  and
and  . With these configurations and with the aid of the five functionals fixed point theorem [20], they established the criteria for the existence of at least triple positive solutions of the above boundary value problem.
. With these configurations and with the aid of the five functionals fixed point theorem [20], they established the criteria for the existence of at least triple positive solutions of the above boundary value problem.
Later on, Yaslan [21], investigated the following boundary value problem:

in which  ,
,  , and
, and  . Indeed, Yaslan analytically established the conditions for the existence of at least two or three positive solutions in the above boundary value problem by means of the Avery-Henderson fixed point theorem and the Leggett-Williams fixed point theorem [22]. As a matter of fact, these analytical results are even new for those special equations on time scales, such as the difference equations with uniform time-step and the ordinary differential equations. Following the work in [21], Sun and Wang [23], further extended the results to the following boundary value problem:
. Indeed, Yaslan analytically established the conditions for the existence of at least two or three positive solutions in the above boundary value problem by means of the Avery-Henderson fixed point theorem and the Leggett-Williams fixed point theorem [22]. As a matter of fact, these analytical results are even new for those special equations on time scales, such as the difference equations with uniform time-step and the ordinary differential equations. Following the work in [21], Sun and Wang [23], further extended the results to the following boundary value problem:

In this paper, inspired by the aforementioned results and methods in dealing with those boundary value problems on time scales, we intend to analytically discuss the possible existence of multiple positive solutions for the following one-dimensional  -Laplacian dynamic equation:
-Laplacian dynamic equation:

with  -point boundary value conditions:
-point boundary value conditions:

In the following discussion, we impose the following three hypotheses.
(H1) for
for  ,
,  , and
, and  , where
, where 
(H2) is left dense continuous (
is left dense continuous ( -continuous), and there exists a
-continuous), and there exists a  such that
such that  .
.  is continuous.
is continuous.
(H3) Both  and
and  are continuously odd functions defined on
are continuously odd functions defined on  . There exist two positive numbers
. There exist two positive numbers  and
and  such that, for any
such that, for any  ,
,

Note that the definition of the  -continuous function will be described in Definition 2.3 of Section 2. Also note that, together with conditions (1.5) and the above hypotheses (H
-continuous function will be described in Definition 2.3 of Section 2. Also note that, together with conditions (1.5) and the above hypotheses (H )–(H
)–(H ), the dynamic equation (1.4) with conditions (1.5) not only includes the above-mentioned specific boundary value problems in literature but also nontrivially extends the situation to a much wider class of boundary value problems on time scales. A question naturally appears: "can we still establish some criteria for the existence of at least double or triple positive solutions in the generalized boundary value problems (1.4) and (1.5)?" In this paper, we will give a positive answer to this question by virtue of the Avery-Henderson fixed point theorem and the five functionals fixed point theorem. Particularly, those obtained criteria will significantly extend the results in literature [19, 21, 23].
), the dynamic equation (1.4) with conditions (1.5) not only includes the above-mentioned specific boundary value problems in literature but also nontrivially extends the situation to a much wider class of boundary value problems on time scales. A question naturally appears: "can we still establish some criteria for the existence of at least double or triple positive solutions in the generalized boundary value problems (1.4) and (1.5)?" In this paper, we will give a positive answer to this question by virtue of the Avery-Henderson fixed point theorem and the five functionals fixed point theorem. Particularly, those obtained criteria will significantly extend the results in literature [19, 21, 23].
The rest of paper is organized as follows. In Section 2, we preliminarily import some definitions and properties of time scales and introduce some useful lemmas which will be utilized in the following discussion. In Section 3, we analytically present a criteria for the existence of at least two positive solutions in the boundary value problems (1.4) and (1.5) by virtue of the Avery-Henderson fixed point theorem. In Section 4, we provide some sufficient conditions for the existence of at least three positive solutions in light of the five functionals fixed point theorem. Finally, we further provides concrete and nontrivial example to illustrate the possible application of the obtained analytical results on dynamic equations on time scales in Section 5.
2. Preliminaries
2.1. Time Scales
For the sake of self-consistency, we import some necessary definitions and lemmas on time scales. More details can be found in [4] and reference therein. First of all, a time scale  is any nonempty closed subset of real numbers
is any nonempty closed subset of real numbers  with order and topological structure defined in a canonical way, as mentioned above. Then, we have the following definition of the categories of points on time scales.
with order and topological structure defined in a canonical way, as mentioned above. Then, we have the following definition of the categories of points on time scales.
Definition 2.1.
For  and
and  , define the forward jump operator
, define the forward jump operator  and the backward jump operator
and the backward jump operator  , respectively, by
, respectively, by

Then, the graininess operator  is defined as
is defined as  In addition, if
In addition, if  ,
,  is said to be right scattered, and if
is said to be right scattered, and if  ,
,  is said to be left scattered. If
is said to be left scattered. If  ,
,  is said to be right dense, and if
is said to be right dense, and if  ,
,  is said to be left dense. If
is said to be left dense. If  has a right scattered minimum
has a right scattered minimum  , denote by
, denote by  ; otherwise, set
; otherwise, set  . If
. If  has a left scattered maximum
has a left scattered maximum  , denote by
, denote by  ; otherwise, set
; otherwise, set  .
.
The following definitions describe the categories of functions on time scales and the basic computations of integral and derivative.
Definition 2.2.
Assume that  is a function and that
is a function and that  .
.  is supposed to be the number (provided it exists) with the property that given any
is supposed to be the number (provided it exists) with the property that given any  ; there is a neighborhood
; there is a neighborhood  of
of  satisfying
satisfying

for all  . Then
. Then  is said to be the delta derivative of
is said to be the delta derivative of  at
at  . Similarly, assume that
. Similarly, assume that  is a function and that
is a function and that  . Denote by
. Denote by  the number (provided it exists) with the property that given any
the number (provided it exists) with the property that given any  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

for all  . Then
. Then  is said to be the nabla derivative of
is said to be the nabla derivative of  at
at  .
.
Definition 2.3.
A function  is left dense continuous (
is left dense continuous ( -continuous) provided that it is continuous at all left dense points of
-continuous) provided that it is continuous at all left dense points of  , and its right side limits exists (being finite) at right dense points of
, and its right side limits exists (being finite) at right dense points of  . Denote by
. Denote by  the set of all left dense continuous functions on
the set of all left dense continuous functions on  .
.
Definition 2.4.
Let  be a function, and
be a function, and  . If there exists a function
. If there exists a function  such that
such that  for all
for all  , then
, then  is a delta antiderivative of
is a delta antiderivative of  . In this case the integral is given by the formula
. In this case the integral is given by the formula

Analogously, let  be a function, and
be a function, and  . If there exists a function
. If there exists a function  such that
such that  for all
for all  , then
, then  is a nabla antiderivative of
is a nabla antiderivative of  . In this case, the integral is given by the formula
. In this case, the integral is given by the formula

2.2. Main Lemmas
This subsection aims to establish several lemmas which are useful in the proof of the main results in this paper. In particular, these lemmas focus on the following linear boundary value problems:


Lemma 2.5.
If  , then, for
, then, for  , the linear boundary value problems (2.6) and (2.7) have a unique solution satisfying
, the linear boundary value problems (2.6) and (2.7) have a unique solution satisfying

 . Here,
. Here,

Proof.
It follows from (2.8) that

Thus, we obtain that

and that

Then,  satisfies (2.6), which verifies that
satisfies (2.6), which verifies that  is a solution of the problems (2.6) and (2.7). Furthermore, in order to show the uniqueness, we suppose that both
is a solution of the problems (2.6) and (2.7). Furthermore, in order to show the uniqueness, we suppose that both  and
and  are the solutions of the problems (2.6) and (2.7). Then, we have
are the solutions of the problems (2.6) and (2.7). Then, we have



In fact, (2.13) further yields

Hence, from (2.14) and (2.16), the assumption  , and the definition of the
, and the definition of the  -Laplacian operator, it follows that
-Laplacian operator, it follows that

This equation, with (2.15), further implies

which consequently leads to the completion of the proof, that is,  specified in (2.8) is the unique solution of the problems (2.6) and (2.7).
specified in (2.8) is the unique solution of the problems (2.6) and (2.7).
Lemma 2.6.
Suppose that  . If
. If  , then the unique solution of the problems (2.6) and (2.7) satisfies
, then the unique solution of the problems (2.6) and (2.7) satisfies

Proof.
Observe that, for any 

Thus, by (2.8) specified in Lemma 2.5, we get

Thus,  is nondecreasing in the interval
is nondecreasing in the interval  . In addition, notice that
. In addition, notice that

The last term in the above estimation is no less than zero owing to those assumptions. Therefore, from the monotonicity of  , we get
, we get

which consequently completes the proof.
Lemma 2.7.
Suppose that  . If
. If  , then the unique positive solution of the problems (2.6) and (2.7) satisfies
, then the unique positive solution of the problems (2.6) and (2.7) satisfies

for  with
with 
Proof.
Since  is nondecreasing in the interval
is nondecreasing in the interval 

On the other hand,

Hence,

This completes the proof.
Now, denote by  and by
and by  , where
, where  . Then, it is easy to verify that
. Then, it is easy to verify that  endowed with
endowed with  becomes a Banach space. Furthermore, define a cone, denoted by
becomes a Banach space. Furthermore, define a cone, denoted by  , through
, through

Also, for a given positive real number  , define a function set
, define a function set  by
by

Naturally, we denote by  and by
and by  . With these settings and notations, we are in a position to have the following properties.
. With these settings and notations, we are in a position to have the following properties.
Lemma 2.8.
If  then (i)
then (i)  for any
for any  ; (ii)
; (ii)  for any pair of
for any pair of  with
with  .
.
The proof of this lemma, which could be found in [19, 21], is directly from the specific construction of the set  . Next, let us construct a map
. Next, let us construct a map  through
through

for any  . Here,
. Here,  . Thus, we obtain the following properties on this map.
. Thus, we obtain the following properties on this map.
Lemma 2.9.
Assume that the hypotheses  are all fulfilled. Then,
are all fulfilled. Then,  and
and  is completely continuous.
is completely continuous.
Proof.
At first, arbitrarily pick up  . Then it directly follows from Lemma 2.6 that
. Then it directly follows from Lemma 2.6 that  for all
for all  . Moreover, direct computation yields
. Moreover, direct computation yields

for all  , and
, and

for all  . Thus, the latter inequality implies that
. Thus, the latter inequality implies that  is decreasing on
is decreasing on  . This implies that
. This implies that  for
for  . Consequently, we complete the proof of the first part of the conclusion that
. Consequently, we complete the proof of the first part of the conclusion that  for any
for any  .
.
Secondly, we are to validate the complete continuity of the map  . To approach this aim, we have to verify that
. To approach this aim, we have to verify that  is bounded, where
is bounded, where  is obviously bounded. It follows from the proof of Lemma 2.7 that
is obviously bounded. It follows from the proof of Lemma 2.7 that

where  . This manifests the uniform boundedness of the set
. This manifests the uniform boundedness of the set  . In addition, for any given
. In addition, for any given  with
with  we have the following estimation:
we have the following estimation:

This validates the equicontinuity of the elements in the set  . Therefore, according to the Arzelà-Ascoli theorem on time scales [2], we conclude that
. Therefore, according to the Arzelà-Ascoli theorem on time scales [2], we conclude that  is relatively compact. Now, let
is relatively compact. Now, let  with
with  . Then
. Then  for all
for all  and
and  Also,
Also,  is uniformly valid on
is uniformly valid on  . These, with the uniform continuity of
. These, with the uniform continuity of  on the compact set
on the compact set  , leads to a conclusion that
, leads to a conclusion that  is uniformly valid on
is uniformly valid on  . Hence, it is easy to verify that
. Hence, it is easy to verify that  as
as  tends toward positive infinity. As a consequence, we complete the whole proof.
tends toward positive infinity. As a consequence, we complete the whole proof.
3. At Least Two Positive Solutions in Boundary Value Problems
This section aims to prove the existence of at least two positive solutions in the boundary value problems (1.4) and (1.5) in light of the well-known Avery-Henderson fixed point theorem. Firstly, we introduce the Avery-Henderson fixed point theorem as follows.
Theorem 3.1 ([24]).
Let  be a cone in a real Banach space
be a cone in a real Banach space  . For each
. For each  , set
, set  . If
. If  and
and  are increasing nonnegative continuous functional on
are increasing nonnegative continuous functional on  , and let
, and let  be a nonnegative continuous functional on
be a nonnegative continuous functional on  with
with  such that, for some
such that, for some  and
and  ,
,

for all  . Suppose that there exist a completely continuous operator
. Suppose that there exist a completely continuous operator  and three positive numbers
and three positive numbers  such that
such that

and (i)  for all
for all  ; (ii)
; (ii)  for all
for all  ; (iii)
; (iii)  and
and  for all
for all  . Then, the operator
. Then, the operator  has at least two fixed points, denoted by
has at least two fixed points, denoted by  and
and  , belonging to
, belonging to  and satisfying
and satisfying  with
with  and
and  with
with  .
.
Secondly, let  and select
and select  satisfying
satisfying  . Furthermore, set, respectively,
. Furthermore, set, respectively,

Then, we arrive at the following results.
Theorem 3.2.
Suppose that the hypotheses  all hold, and that there exist positive real numbers
all hold, and that there exist positive real numbers  ,
,  ,
,  such that
such that

In addition, suppose that  satisfies the following conditions:
satisfies the following conditions:
(B1) for
for  and
and  ;
;
(B2) for
for  and
and  ;
;
(B3) for
for  and
and 
Then, the boundary value problems (1.4) and (1.5) have at least two positive solutions  and
and  such that
such that

Proof.
Construct the cone  and the operator
and the operator  as specified in (2.28) and (2.30), respectively. In addition, define the increasing, nonnegative, and continuous functionals
as specified in (2.28) and (2.30), respectively. In addition, define the increasing, nonnegative, and continuous functionals  ,
,  , and
, and  on
on  , respectively, by
, respectively, by

Obviously,  for each
for each  .
.
Moreover, Lemma 2.8 manifests that  for each
for each  . Hence, we have
. Hence, we have

for each  . Also, notice that
. Also, notice that  for
for  and
and  . Furthermore, from Lemma 2.9, it follows that the operator
. Furthermore, from Lemma 2.9, it follows that the operator  is completely continuous.
is completely continuous.
Next, we are to verify the validity of all the conditions in Theorem 3.1 with respect to the operator  .
.
Let  . Then,
. Then,  . This implies
. This implies  for
for  , which, combined with (3.7), yields
, which, combined with (3.7), yields

for  . Noticing the assumption (
. Noticing the assumption ( ), we have
), we have  for
for  . Also noticing the particular form in (2.30), Lemma 2.8, the property
. Also noticing the particular form in (2.30), Lemma 2.8, the property  , and the proof of Lemma 2.7, we get
, and the proof of Lemma 2.7, we get

Therefore, condition (i) in Theorem 3.1 is satisfied.
In what follows, let us consider  . In such a case, we obtain
. In such a case, we obtain  , which means that
, which means that  for
for  . Similarly, it follows from (3.7) that, for all
. Similarly, it follows from (3.7) that, for all  ,
,

Hence, we have  for
for  . This, combined with the assumption (
. This, combined with the assumption ( ), yields
), yields  for all
for all  . Therefore, from the proof of Lemma 2.7, we have
. Therefore, from the proof of Lemma 2.7, we have

which consequently leads to the validity of condition (ii) in Theorem 3.1.
Last, let us notice that the constant functions  . Then,
. Then,  . Take
. Take  . We thus obtain
. We thus obtain  . This, with the assumption
. This, with the assumption  , manifests that
, manifests that  and
and  for all
for all  . Analogously, we can get
. Analogously, we can get

which shows the validity of condition (iii) in Theorem 3.1.
Now, in the light of Theorem 3.1, we consequently arrive to the conclusion that the boundary value problems (1.4) and (1.5) admit at least two positive solutions, denoted by  and
and  , satisfying
, satisfying  with
with  , and
, and  with
with  , respectively.
, respectively.
4. At Least Three Positive Solutions in Boundary Value Problems
By means of the five functionals fixed point theorem which is attributed to Avery [20], this section is to analytically prove the existence of at least three positive solutions in the boundary value problems (1.4) and (1.5).
Take  as nonnegative continuous convex functionals on
as nonnegative continuous convex functionals on  . Both
. Both  and
and  are supposed to be nonnegative continuous concave functionals on
are supposed to be nonnegative continuous concave functionals on  . Then, for nonnegative real numbers
. Then, for nonnegative real numbers  ,
,  ,
,  ,
,  , and
, and  , construct five convex sets, respectively, through
, construct five convex sets, respectively, through

Theorem 4.1 ([20]).
Let  be a cone in a real Banach space
be a cone in a real Banach space  . Suppose that
. Suppose that  and
and  are nonnegative continuous concave functionals on
are nonnegative continuous concave functionals on  , and that
, and that  ,
,  , and
, and  are nonnegative continuous convex functionals on
are nonnegative continuous convex functionals on  such that, for some positive numbers
such that, for some positive numbers  and
and  ,
,

for all  . In addition, suppose that
. In addition, suppose that  is a completely continuous operator and that there exist nonnegative real numbers
is a completely continuous operator and that there exist nonnegative real numbers  with
with  such that
such that
-
(i)
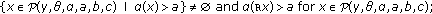
-
(ii)
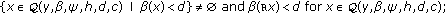
-
(iii)

-
(iv)

Then the operator  admits at least three fixed points
admits at least three fixed points  ,
, ,
, satisfying
satisfying  ,
,  , and
, and  with
with  , respectively.
, respectively.
In the light of this theorem, we can have the following result on the existence of at least three solutions in the boundary value problems (1.4) and (1.5).
Theorem 4.2.
Suppose that the hypotheses  are all fulfilled. Also suppose that there exist positive real numbers
are all fulfilled. Also suppose that there exist positive real numbers  ,
,  , and
, and  such that
such that

Furthermore, let  satisfies the following conditions:
satisfies the following conditions:
(C1) for
for  and
and  ;
;
(C2) for
for  and
and  ;
;
(C3) for
for  and
and  .
.
Then, the boundary value problems (1.4) and (1.5) possess at least three solutions  ,
,  , and
, and  , defined on
, defined on  , satisfying, respectively,
, satisfying, respectively,

Proof.
Set the cone  as constructed in (2.28) and the operator
as constructed in (2.28) and the operator  as defined in (2.30). Take, respectively, the nonnegative continuous concave functionals on the
as defined in (2.30). Take, respectively, the nonnegative continuous concave functionals on the  as follows:
as follows:

Then, we get  for
for  . Besides, from Lemma 2.8, it follows that
. Besides, from Lemma 2.8, it follows that

for  . In what follows, we aim to show the validity of all the conditions in Theorem 4.1 with respect to the operator
. In what follows, we aim to show the validity of all the conditions in Theorem 4.1 with respect to the operator  .
.
To this end, arbitrarily take a function  . Thus,
. Thus,  , which, combined with (4.6), gives
, which, combined with (4.6), gives  for
for  and
and  . Hence, we have
. Hence, we have  for
for  , due to the assumption (
, due to the assumption ( ). Furthermore, since
). Furthermore, since  , in the light of the proof of Lemma 2.7, we have
, in the light of the proof of Lemma 2.7, we have

So, according to Lemma 2.9, we have the complete continuity of the operator  .
.
Moreover, the set

is not empty, since the constant function  is contained in the set
is contained in the set  . Similarly, the set
. Similarly, the set

is nonempty because of  . For a particular
. For a particular  , the implementation of (4.6) gives
, the implementation of (4.6) gives

for  . The utilization of the assumption (
. The utilization of the assumption ( ) leads us to the inequality
) leads us to the inequality

Thus, it follows from (4.11) and Lemmas 2.7 and 2.8 that

Clearly, we verify the validity of condition ( ) in Theorem 4.1.
) in Theorem 4.1.
Next, consider  . In such a case, we obtain
. In such a case, we obtain

for  . Imposing the assumption (
. Imposing the assumption ( ) produces
) produces  . Moreover, by the proof of Lemma 2.7, we obtain
. Moreover, by the proof of Lemma 2.7, we obtain

Therefore, we further verify the validity of condition ( ) in Theorem 4.1.
) in Theorem 4.1.
Finally, we are to validate conditions ( ) and (
) and ( ) aside from conditions (
) aside from conditions ( ) and (
) and ( ). For this purpose, on the one hand, let us consider
). For this purpose, on the one hand, let us consider  with
with  . Then, we have
. Then, we have

On the other hand, consider  with
with  . In this case, we get
. In this case, we get

Accordingly, both conditions ( ) and (
) and ( ) in Theorem 4.1 are satisfied. Now, in light of Theorem 4.1, the boundary value problems (1.4) and (1.5) have at least three positive solutions circumscribed on
) in Theorem 4.1 are satisfied. Now, in light of Theorem 4.1, the boundary value problems (1.4) and (1.5) have at least three positive solutions circumscribed on  satisfying
satisfying  ,
,  , and
, and  with
with  .
.
5. An Illustrative Example
This section will provide a nontrivial example to clearly illustrate the feasibility of the above-established analytical results on the dynamic equations on time scales.
First of all, construct a nontrivial time scale set as  . Set all the parameters in problems (1.4) and (1.5) as follows:
. Set all the parameters in problems (1.4) and (1.5) as follows:  , and
, and  , so that
, so that  . For simplicity but without loss of generality, set
. For simplicity but without loss of generality, set  . we can obtain
. we can obtain

In particular, set the function in dynamic equation as

This setting allows us to properly take the other parameters as  ,
,  , and
, and  . It is clear that these parameters satisfy
. It is clear that these parameters satisfy

To this end, we can verify the validity of conditions  in Theorem 4.2. As a matter of fact, direct calculations produce
in Theorem 4.2. As a matter of fact, direct calculations produce

as  and
and  ,
,

as  and
and  , and
, and

 and
and  . Accordingly, conditions
. Accordingly, conditions in Theorem 4.2 are satisfied for the above specified functions and parameters. Now, by virtue of Theorem 4.2, we can approach a conclusion that the dynamic equation on the specified time scales
in Theorem 4.2 are satisfied for the above specified functions and parameters. Now, by virtue of Theorem 4.2, we can approach a conclusion that the dynamic equation on the specified time scales

with the boundary conditions

possesses at least three positive solutions defined on  satisfying
satisfying  ,
,  , and
, and  with
with  .
.
References
Aulbach B, Hilger S: Linear dynamic processes with inhomogeneous time scale. In Nonlinear Dynamics and Quantum Dynamical Systems (Gaussig, 1990), Mathematical Research. Volume 59. Akademie, Berlin, Germany; 1990:9-20.
Agarwal RP, Bohner M, Rehák P: Half-linear dynamic equations. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Vol. 1, 2. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:1-57.
Agarwal RP, O'Regan D: Nonlinear boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2001,44(4):527-535. 10.1016/S0362-546X(99)00290-4
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterosn A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Atici FM, Biles DC, Lebedinsky A: An application of time scales to economics. Mathematical and Computer Modelling 2006,43(7-8):718-726. 10.1016/j.mcm.2005.08.014
Hoffacker J, Tisdell CC: Stability and instability for dynamic equations on time scales. Computers & Mathematics with Applications 2005,49(9-10):1327-1334. 10.1016/j.camwa.2005.01.016
Zhong W, Lin W, Ruan J: The generalized invariance principle for dynamic equations on time scales. Applied Mathematics and Computation 2007,184(2):557-565. 10.1016/j.amc.2006.06.056
Anderson DR: Solutions to second-order three-point problems on time scales. Journal of Difference Equations and Applications 2002,8(8):673-688. 10.1080/1023619021000000717
Anderson D, Avery R, Davis J, Henderson J, Yin W: Positive solutions of boundary value problems. In Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:189-249.
Anderson DR: Nonlinear triple-point problems on time scales. Electronic Journal of Differential Equations 2004, 47: 1-12.
DaCunha JJ, Davis JM, Singh PK: Existence results for singular three point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004,295(2):378-391. 10.1016/j.jmaa.2004.02.049
Kaufmann ER: Positive solutions of a three-point boundary-value problem on a time scale. Electronic Journal of Differential Equations 2003, 82: 1-11.
He Z:Existence of two solutions of
 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051Yaslan İ: Existence of positive solutions for nonlinear three-point problems on time scales. Journal of Computational and Applied Mathematics 2007,206(2):888-897. 10.1016/j.cam.2006.08.033
Sun H-R, Li W-T:Multiple positive solutions for
 -Laplacian
-Laplacian  -point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009
-point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009He Z:Double positive solutions of three-point boundary value problems for
 -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012
-Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012Su Y-H, Li W-T:Triple positive solutions of
 -point BVPs for
-point BVPs for  -Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018
-Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018He Z, Li L:Multiple positive solutions for the one-dimensional
 -Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021
-Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021Avery RI: A generalization of the Leggett-Williams fixed point theorem. Mathematical Sciences Research Hot-Line 1999,3(7):9-14.
Yaslan İ: Multiple positive solutions for nonlinear three-point boundary value problems on time scales. Computers & Mathematics with Applications 2008,55(8):1861-1869. 10.1016/j.camwa.2007.07.005
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana University Mathematics Journal 1979,28(4):673-688. 10.1512/iumj.1979.28.28046
Sun H-R, Wang Y-H:Existence of positive solutions for
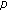 -Laplacian three-point boundary-value problems on time scales. Electronic Journal of Differential Equations 2008, 92: 1-14.
-Laplacian three-point boundary-value problems on time scales. Electronic Journal of Differential Equations 2008, 92: 1-14.Avery RI, Henderson J: Two positive fixed points of nonlinear operators on ordered Banach spaces. Communications on Applied Nonlinear Analysis 2001,8(1):27-36.
Acknowledgments
The authors are grateful to the two anonymous referees and Professor Alberto Cabada for their significant suggestions on the improvement of this paper. This work was supported by the NNSF of China (Grant nos. 10501008 and 60874121) and by the Rising-Star Program Foundation of Shanghai, China (Grant no. 07QA14002).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhong, W., Lin, W. Existence of Positive Solutions in Generalized Boundary Value Problem for  -Laplacian Dynamic Equations on Time Scales.
Adv Differ Equ 2009, 848191 (2009). https://doi.org/10.1155/2009/848191
-Laplacian Dynamic Equations on Time Scales.
Adv Differ Equ 2009, 848191 (2009). https://doi.org/10.1155/2009/848191
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/848191
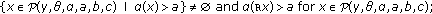
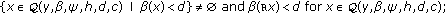


 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051 -Laplacian
-Laplacian  -point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009
-point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009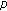 -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012
-Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012 -point BVPs for
-point BVPs for  -Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018
-Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018 -Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021
-Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021 -Laplacian three-point boundary-value problems on time scales. Electronic Journal of Differential Equations 2008, 92: 1-14.
-Laplacian three-point boundary-value problems on time scales. Electronic Journal of Differential Equations 2008, 92: 1-14.