- Research Article
- Open access
- Published:
Summation Characterization of the Recessive Solution for Half-Linear Difference Equations
Advances in Difference Equations volume 2009, Article number: 521058 (2009)
Abstract
We show that the recessive solution of the second-order half-linear difference equation  ,
,  ,
,  , where
, where  are real-valued sequences, is closely related to the divergence of the infinite series
are real-valued sequences, is closely related to the divergence of the infinite series  .
.
1. Introduction
We consider the second-order half-linear difference equation

where  are real-valued sequences and
are real-valued sequences and  and we investigate properties of itsrecessive solution.
and we investigate properties of itsrecessive solution.
Qualitative theory of (1.1) was established in the series of the papers of  ehák [1–5] and it is summarized in [6, Chapter 3]. It was shown there that the oscillation theory of (1.1) is very similar to that of the linear equation
ehák [1–5] and it is summarized in [6, Chapter 3]. It was shown there that the oscillation theory of (1.1) is very similar to that of the linear equation

which is the special case  in (1.1). We will recall basic facts of the oscillation theory of (1.1) in the following section.
in (1.1). We will recall basic facts of the oscillation theory of (1.1) in the following section.
The concept of the recessive solution of (1.1) has been introduced in [7]. There are several attempts in literature to find a summation characterization of this solution, see [8] and also related references [9, 10], which are based on the asymptotic analysis of solutions of (1.1). However, this approach requires the sign restriction of the sequence  and additional assumptions on the convergence (divergence) of certain infinite series involving sequences
and additional assumptions on the convergence (divergence) of certain infinite series involving sequences  and
and  see Proposition 2.1 in the following section. Here we use a different approach which is based on estimates for a certain nonlinear function which appears in the Picone-type identity for (1.1).
see Proposition 2.1 in the following section. Here we use a different approach which is based on estimates for a certain nonlinear function which appears in the Picone-type identity for (1.1).
The recessive solution of (1.1) is a discrete counterpart of the concept of the principal solution of the half-linear differential equation

which attracted considerable attention in recent years, we refer to the work in [11–15] and the references given therein.
Let us recall the main result of [11] whose discrete version we are going to prove in this paper.
Proposition 1.1.
Let  be a solution of (1.3) such that
be a solution of (1.3) such that  for large
for large  .
.
-
(i)
Let
 . If
. If (1.4)
(1.4)then
 is the principal solution of (1.3).
is the principal solution of (1.3). -
(ii)
If
 and
and  , then
, then 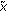 is not the principal solution of (1.3).
is not the principal solution of (1.3).
The paper is organized as follows. In Section 2 we recall elements of the oscillation theory of (1.1). Section 3 is devoted to technical statements which we use in the proofs of our main results which are presented in Section 4. Section 5 contains formulation of open problems in our research.
2. Preliminaries
Oscillatory properties of (1.1) are defined using the concept of the generalized zero which is defined in the same way as for (1.2), see, for example, [6, Chapter 3],or [16, Chapter 7]. A solution  of (1.1) has a generalized zero in an interval
of (1.1) has a generalized zero in an interval  if
if  and
and  . Since we suppose that
. Since we suppose that  (oscillation theory of (1.1) generally requires only
(oscillation theory of (1.1) generally requires only  ), a generalized zero of
), a generalized zero of  in
in  is either a "real" zero at
is either a "real" zero at  or the sign change between
or the sign change between  and
and  . However, (1.1) is said to be disconjugate in a discrete interval
. However, (1.1) is said to be disconjugate in a discrete interval  if the solution
if the solution  of (1.1) given by the initial condition
of (1.1) given by the initial condition  ,
,  has no generalized zero in
has no generalized zero in  . However, (1.1) is said to be nonoscillatory if there exists
. However, (1.1) is said to be nonoscillatory if there exists  such that it is disconjugate on
such that it is disconjugate on  for every
for every  and is said to be oscillatory in the opposite case.
and is said to be oscillatory in the opposite case.
If  is a solution of (1.1) such that
is a solution of (1.1) such that  in some discrete interval
in some discrete interval  then
then  is a solution of the associated Riccati type equation
is a solution of the associated Riccati type equation

where  is the inverse function of
is the inverse function of  and
and  is the conjugate number to
is the conjugate number to  . Moreover, if
. Moreover, if  has no generalized zero in
has no generalized zero in  then
then  ,
,  . If we suppose that (1.1) is nonoscillatory, among all solutions of (2.1) there exists the so-calleddistinguished solution
. If we suppose that (1.1) is nonoscillatory, among all solutions of (2.1) there exists the so-calleddistinguished solution  which has the property that there exists an interval
which has the property that there exists an interval  such that any other solution
such that any other solution  of (2.1) for which
of (2.1) for which  ,
,  , satisfies
, satisfies  ,
,  . Therefore, the distinguished solution of (2.1) is, in a certain sense, minimal solution of this equation near
. Therefore, the distinguished solution of (2.1) is, in a certain sense, minimal solution of this equation near  and sometimes it is called theminimal solution of (2.1). If
and sometimes it is called theminimal solution of (2.1). If  is the distinguished solution of (2.1), then the associated solution of (1.1) given by the formula
is the distinguished solution of (2.1), then the associated solution of (1.1) given by the formula

is said to be the recessive solution of (1.1), see [7]. Note that in the linear case  a solution
a solution  of (1.2) is recessive if and only if
of (1.2) is recessive if and only if

At the end of this section, for the sake of comparison, we recall the main results of [8, 17], where summation characterizations of recessive solutions of (1.1) are investigated using the asymptotic analysis of the solution space of (1.1).
Proposition 2.1.
Let  be a solution of (1.1).
be a solution of (1.1).
-
(i)
Suppose that
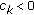 , then
, then  is the recessive solution of (1.1) if and only if
is the recessive solution of (1.1) if and only if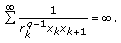 (2.4)
(2.4) -
(ii)
Suppose that
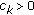 ,
, 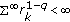 , and
, and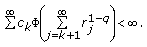 (2.5)
(2.5)If
 is the recessive solution of (1.1), then
is the recessive solution of (1.1), then (2.6)
(2.6) -
(iii)
Suppose that
 ,
, 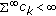 , and
, and 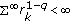 . Then
. Then  is the recessive solution if and only if (2.4) holds.
is the recessive solution if and only if (2.4) holds.
In cases (i) and (iii), the previous proposition givesnecessary and sufficient condition for a solution  to be recessive. The reason why under assumptions in (i) or (iii) it is possible to formulate such a condition is that there is a substantial difference in asymptotic behavior of recessive and dominant solutions (i.e., solutions which are linearly independent of the recessive solution). This difference enables to "separate" the recessive solution from dominant ones and to formulate for it a necessary and sufficient condition (2.4). We refer to [8, 17] and also to [9, 10] for more details.
to be recessive. The reason why under assumptions in (i) or (iii) it is possible to formulate such a condition is that there is a substantial difference in asymptotic behavior of recessive and dominant solutions (i.e., solutions which are linearly independent of the recessive solution). This difference enables to "separate" the recessive solution from dominant ones and to formulate for it a necessary and sufficient condition (2.4). We refer to [8, 17] and also to [9, 10] for more details.
3. Technical Results
Throughout the rest of the paper we suppose that (1.1) is nonoscillatory and  is its solution. Denote
is its solution. Denote

and define the function

Lemma 3.1.
Put

where  is a solution of (2.1) and
is a solution of (2.1) and  is any sequence satisfying
is any sequence satisfying  . Then the following statements hold:
. Then the following statements hold:
-
(i)
 is a solution of (2.1) if and only if
is a solution of (2.1) if and only if 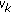 is a solution of
is a solution of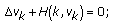 (3.4)
(3.4) -
(ii)
 for
for  with the equality if and only if
with the equality if and only if 
-
(iii)
 if and only if
if and only if 
-
(iv)
let
 be a solution of (3.4) and suppose that
be a solution of (3.4) and suppose that  for some
for some 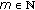 , that is,
, that is,  , then
, then  if and only if
if and only if 
Proof.
The statements (i), (ii) are consequences of [18, Lemma 2.5].
 We have
We have

 We have
We have

Denote by  the expression in brackets, then
the expression in brackets, then

Consequently,

that is, the statement holds according to the statement (iii) of this lemma.
Lemma 3.2.
Let  be defined by (3.1), (3.2) and suppose that
be defined by (3.1), (3.2) and suppose that  for large
for large  . Then one has the following inequalities for large
. Then one has the following inequalities for large  .
.
If  , then
, then  and
and

If  , then
, then  and
and

Proof.
We have (with using the Lagrange mean value theorem)

where  and hence
and hence  .
.
Thus, if  ,
,

and in the case  we obtain
we obtain

Next we proceed similarly as in [18, Lemma 2.6]. Inequalities (3.9), (3.10) can be written in the equivalent forms:


Denote  and let
and let  . Then
. Then

Consequently,  and
and

Hence, in view of the assumption  ,
,  . It follows that
. It follows that

in some left neighborhood of  and the function
and the function  is positive, decreasing, and convex for
is positive, decreasing, and convex for  and is negative, increasing, and concave for
and is negative, increasing, and concave for  (with respect to
(with respect to  ). Hence, both the inequalities (3.14) and (3.15) are satisfied in some left neighborhood of
). Hence, both the inequalities (3.14) and (3.15) are satisfied in some left neighborhood of  The proof will be completed by showing that
The proof will be completed by showing that  has constant sign on the given intervals. By a direct computation,
has constant sign on the given intervals. By a direct computation,

where

Hence

and from (3.18)

in some left neighborhood of  .
.
Moreover, for 

and  (for
(for  ) if and only if
) if and only if

Next we distinguish between the cases  and
and  .
.
If  , then using (3.12),
, then using (3.12),

hence  is decreasing on
is decreasing on  and in view of (3.22) it means that
and in view of (3.22) it means that  and consequently from (3.21) also
and consequently from (3.21) also  is positive for
is positive for  . Hence, (3.14) holds.
. Hence, (3.14) holds.
Similarly, if  , then
, then

hence  is increasing for
is increasing for  and from (3.22) we have that
and from (3.22) we have that  and hence also
and hence also  is negative for
is negative for  . This means that (3.15) is satisfied.
. This means that (3.15) is satisfied.
4. Main Results
Theorem 4.1.
Suppose  and let
and let  be a solution of (1.1) such that
be a solution of (1.1) such that  for large
for large  . If
. If

then  is the recessive solution.
is the recessive solution.
Proof.
Denote by  the associated solution of (2.1) and let
the associated solution of (2.1) and let  be a solution of (2.1) generated by another solution (linearly independent of
be a solution of (2.1) generated by another solution (linearly independent of  ) of (1.1). Then, it follows from Lemma 3.1 that
) of (1.1). Then, it follows from Lemma 3.1 that  is a solution of (3.4), that is,
is a solution of (3.4), that is,

and suppose that this solution satisfies the condition  This means that
This means that  and to prove that
and to prove that  is the recessive solution of (1.1), we need to show that there exists
is the recessive solution of (1.1), we need to show that there exists  such that
such that  , that is, according to Lemma 3.1,
, that is, according to Lemma 3.1,  . Suppose by contradiction that
. Suppose by contradiction that  for
for  . According to Lemma 3.1 (iv), it means that
. According to Lemma 3.1 (iv), it means that  for
for  , that is,
, that is,  . Then we have from Lemma 3.2 that
. Then we have from Lemma 3.2 that  and
and

Next, consider the equation

and let  be its solution satisfying
be its solution satisfying  . However, (4.4) is equivalent to
. However, (4.4) is equivalent to

that is,

where we have substituted for  from (4.4) in the denominator. Hence
from (4.4) in the denominator. Hence

and we obtain

Condition (4.1) implies that there exists  such that
such that  and either
and either  or
or  is not defined. This means that
is not defined. This means that  (from (4.4)). On the other hand, (4.3) together with (4.4) and the fact that
(from (4.4)). On the other hand, (4.3) together with (4.4) and the fact that  is increasing with respect to
is increasing with respect to  on
on  imply that
imply that  for
for  Since
Since  for
for  we have
we have  for
for  a contradiction.
a contradiction.
Theorem 4.2.
Suppose  and let
and let  be a solution of (1.1) such that
be a solution of (1.1) such that  for large
for large  . If
. If

then  is not the recessive solution.
is not the recessive solution.
Proof.
Similarly, as in the proof of Theorem 4.1, denote  and let
and let  be a solution of (2.1) generated by another solution (linearly independent of
be a solution of (2.1) generated by another solution (linearly independent of  ) of (1.1). Then
) of (1.1). Then  is a solution of (3.4), that is,
is a solution of (3.4), that is,

and suppose that this solution satisfies the condition  ,
,  being sufficiently small (will be specified later). Hence
being sufficiently small (will be specified later). Hence  and we have to show that
and we have to show that  for
for  , that is,
, that is,  for
for 
Let  be a solution of (4.4) and suppose that
be a solution of (4.4) and suppose that  . Hence, similarly as in the proof of Theorem 4.1, we obtain
. Hence, similarly as in the proof of Theorem 4.1, we obtain

If  is sufficiently small, then condition (4.9) implies that
is sufficiently small, then condition (4.9) implies that  for
for  and from (4.4), we have
and from (4.4), we have  for
for  . Consequently, from Lemma 3.2 we obtain that
. Consequently, from Lemma 3.2 we obtain that  and
and

Moreover, since  is increasing with respect to
is increasing with respect to  on
on  we obtain from (4.12) that
we obtain from (4.12) that  for
for  Hence
Hence  for
for  and hence also
and hence also  for
for 
5. Applications and Open Problems
(i)Theorems 4.1 and 4.2, as formulated in the previous section, apply only to positive decreasing (or negative increasing) solutions of (1.1). The reason is that we have been able to prove inequalities (3.9), (3.10) only when  . We conjecture that Theorems 4.1 and 4.2 remain to hold forevery solution of (1.1) for which
. We conjecture that Theorems 4.1 and 4.2 remain to hold forevery solution of (1.1) for which  for large
for large  . To justify this conjecture, consider the function
. To justify this conjecture, consider the function

By an easy computation one can find that inequalities (3.9), (3.10) are equivalent to the inequalities

However, if  , that is,
, that is,  , we have
, we have

so inequalities (3.9), (3.10) are no longer valid in this case. Numerical computations together with a closer examination of the graph of the function  lead to the following conjecture.
lead to the following conjecture.
Conjecture 5.1.
Let  ,
,  , and
, and  Then for
Then for  one has
one has

To explain this conjecture in more details, consider the case  , the case
, the case  can be treated analogically. We have (we skip the index
can be treated analogically. We have (we skip the index  , only indices different from
, only indices different from  are written explicitly)
are written explicitly)

where  If
If  , the direct substitution yields
, the direct substitution yields

If  , then
, then  and we proceed as follows. For
and we proceed as follows. For  , the function
, the function  is concave for nonnegative arguments, so for
is concave for nonnegative arguments, so for  we have the inequality
we have the inequality

We substitute  ,
,  , then
, then  , that is,
, that is,  . Hence we have
. Hence we have

Hence

Next we prove that  for
for  . Denote
. Denote  , then we need to prove the inequality
, then we need to prove the inequality  for
for  . A standard investigation of the graph of the function
. A standard investigation of the graph of the function  shows that the required inequality really holds, so we have
shows that the required inequality really holds, so we have

By a similar computation we find that

These computations lead to the conjecture that  attains its global minimum at a point in
attains its global minimum at a point in  if
if  and at a point in
and at a point in  if
if  . Numerical computations suggest that this minimum is
. Numerical computations suggest that this minimum is  , where
, where  .
.
Having proved inequalities (5.4), Theorems 4.1 and 4.2 could be proved for any positive  with
with  in the same way as in the previous section, it is only sufficient to replace
in the same way as in the previous section, it is only sufficient to replace  by
by  .
.
(ii)A typical example of (1.1) to which Theorems 4.1 and 4.2 apply is (1.1) with

since under these assumption all positive solutions of (1.1) are decreasing, see [19]. However, one can applyindirectly Theorems 4.1 and 4.2 also to (1.1) with

(and  , otherwise (1.1) would be oscillatory, see [16, Theorem 8.2.14] ), even if all positive solutions of (1.1) areincreasing in this case. The method which enables to overcome this difficulty is the so-calledreciprocity principle, which can be explained as follows.
, otherwise (1.1) would be oscillatory, see [16, Theorem 8.2.14] ), even if all positive solutions of (1.1) areincreasing in this case. The method which enables to overcome this difficulty is the so-calledreciprocity principle, which can be explained as follows.
Suppose that  in (1.1) and let
in (1.1) and let  . Then by a direct computation one can verify that
. Then by a direct computation one can verify that  solves the so-calledreciprocal equation:
solves the so-calledreciprocal equation:

Moreover, if  does not change its sign for large
does not change its sign for large  , (1.1) is nonoscillatory if and only if (5.14) is nonoscillatory, see [9]. The following statement relates recessive solutions of (1.1) and (5.14). A similar statement can be found in [9], but our proof differs from that given in [9].
, (1.1) is nonoscillatory if and only if (5.14) is nonoscillatory, see [9]. The following statement relates recessive solutions of (1.1) and (5.14). A similar statement can be found in [9], but our proof differs from that given in [9].
Theorem 5.2.
Suppose that (1.1) is nonoscillatory and (5.12) or (5.13) holds. If a solution  of (1.1) is recessive, then
of (1.1) is recessive, then  is the recessive solution of (5.14).
is the recessive solution of (5.14).
Proof.
First suppose that (5.13) holds and let  be the distinguished solution of (2.1). Assumption (5.13) implies that
be the distinguished solution of (2.1). Assumption (5.13) implies that  for large
for large  , see [7]. The solution
, see [7]. The solution  of the Riccati equation
of the Riccati equation

associated with (5.14) is given by  and we have the following relationship between solutions of (5.15) and (2.1) (no index means again the index
and we have the following relationship between solutions of (5.15) and (2.1) (no index means again the index  ):
):

Since the function

is increasing for  the inequality
the inequality  for large
for large  and for any solution
and for any solution  of (2.1) implies the inequality
of (2.1) implies the inequality  where
where

and  is any other solution of (5.15). Consequently,
is any other solution of (5.15). Consequently,  is the distinguished solution of (5.15) and hence
is the distinguished solution of (5.15) and hence  is the recessive solution of (5.14).
is the recessive solution of (5.14).
Now suppose that (5.12) holds. Then all solutions  of (2.1) satisfying
of (2.1) satisfying  for large
for large  are negative (see [19]), that is,
are negative (see [19]), that is,  . Then using the same argument as in the first part of the proof we have
. Then using the same argument as in the first part of the proof we have  for large
for large  for any solution
for any solution  of (5.15), that is,
of (5.15), that is,  is the recessive solution of (5.14).
is the recessive solution of (5.14).
(iii)In [18], we posed the question whether the sequence  is the recessive solution of the difference equation
is the recessive solution of the difference equation

Now we can give the affirmative answer to this question for  . It is shown in [18] that
. It is shown in [18] that

both as  . The sequence
. The sequence  is a solution of the equation
is a solution of the equation

which is reciprocal to (5.19) and  is a solution of the equation
is a solution of the equation

which is reciprocal to (5.21) and differs from (5.19) only by the shift  in the sequence
in the sequence  . Since
. Since

assumption (5.12) is satisfied (with  ,
,  , and
, and  instead of
instead of  ,
,  , and
, and  , resp.), hence positive solutions of (5.21) are decreasing, that is, Theorems 4.1 and 4.2 apply to this case. By a direct computation, we have
, resp.), hence positive solutions of (5.21) are decreasing, that is, Theorems 4.1 and 4.2 apply to this case. By a direct computation, we have

This means, by Theorem 4.1, that if  , then
, then  is the recessive solution of (5.21) and hence
is the recessive solution of (5.21) and hence  is the recessive solution of (5.22). Consequently,
is the recessive solution of (5.22). Consequently,  is the recessive solution of (5.19) if
is the recessive solution of (5.19) if  .
.
References
Řehák P: Hartman-Wintner type lemma, oscillation, and conjugacy criteria for half-linear difference equations. Journal of Mathematical Analysis and Applications 2000,252(2):813-827. 10.1006/jmaa.2000.7124
Řehák P: Oscillatory properties of second order half-linear difference equations. Czechoslovak Mathematical Journal 2001,51(2):303-321. 10.1023/A:1013790713905
Řehák P: Generalized discrete Riccati equation and oscillation of half-linear difference equations. Mathematical and Computer Modelling 2001,34(3-4):257-269. 10.1016/S0895-7177(01)00059-0
Řehák P: Oscillation criteria for second order half-linear difference equations. Journal of Difference Equations and Applications 2001,7(4):483-505. 10.1080/10236190108808284
Řehák P: Oscillation and nonoscillation criteria for second order linear difference equations. Fasciculi Mathematici 2001, (31):71-89.
Agarwal RP, Bohner M, Grace SR, O'Regan D: Discrete Oscillation Theory. Hindawi, New York, NY, USA; 2005.
Došlý O, Řehák P: Recessive solution of half-linear second order difference equations. Journal of Difference Equations and Applications 2003,9(1):49-61.
Cecchi M, Došlá Z, Marini M: Nonoscillatory half-linear difference equations and recessive solutions. Advances in Difference Equations 2005, (2):193-204.
Cecchi M, Došlá Z, Marini M: Reciprocity principle and asymptotic properties of solutions of half-linear difference equations. submitted
Cecchi M, Došlá Z, Marini M, Vrkoč I: Asymptotic properties for half-linear difference equations. Mathematica Bohemica 2006,131(4):347-363.
Došlý O, Elbert Á: Integral characterization of the principal solution of half-linear second order differential equations. Studia Scientiarum Mathematicarum Hungarica 2000,36(3-4):455-469.
Cecchi M, Došlá Z, Marini M: Half-linear equations and characteristic properties of the principal solution. Journal of Differential Equations 2005,208(2):494-507. 10.1016/j.jde.2004.04.004
Cecchi M, Došlá Z, Marini M: Corrigendum to: "Half-linear equations and characteristic properties of the principal solution". Journal of Differential Equations 2006,221(1):272-274. 10.1016/j.jde.2005.10.020
Cecchi M, Došlá Z, Marini M: Limit and integral properties of principal solutions for half-linear differential equations. Archivum Mathematicum 2007,43(1):75-86.
Elbert Á, Kusano T: Principal solutions of non-oscillatory half-linear differential equations. Advances in Mathematical Sciences and Applications 1998,8(2):745-759.
Došlý O, Řehák P: Half-linear Differential Equations, North-Holland Mathematics Studies. Volume 202. Elsevier, Amsterdam, The Netherlands; 2005.
Cecchi M, Došlá Z, Marini M: On recessive and dominant solutions for half-linear difference equations. Journal of Difference Equations and Applications 2004,10(9):797-808. 10.1080/10236190310001634785
Došlý O, Fišnarová S: Linearized Riccati technique and (non-)oscillation criteria for half-linear difference equations. Advances in Difference Equations 2008, 2008:-18.
Li W-T: Classification schemes for nonoscillatory solutions of two-dimensional nonlinear difference systems. Computers & Mathematics with Applications 2001,42(3–5):341-355.
Acknowledgments
This research is supported by the Grant 201/07/0145 of the Czech Grant Agency of the Czech Republic, and the Research Project MSM0022162409 of the Czech Ministry of Education.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Došlý, O., Fišnarová, S. Summation Characterization of the Recessive Solution for Half-Linear Difference Equations. Adv Differ Equ 2009, 521058 (2009). https://doi.org/10.1155/2009/521058
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/521058
 . If
. If
 is the principal solution of (1.3).
is the principal solution of (1.3). and
and  , then
, then 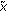 is not the principal solution of (1.3).
is not the principal solution of (1.3).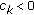 , then
, then  is the recessive solution of (1.1) if and only if
is the recessive solution of (1.1) if and only if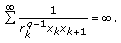
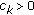 ,
, 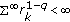 , and
, and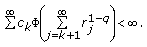
 is the recessive solution of (1.1), then
is the recessive solution of (1.1), then
 ,
, 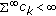 , and
, and 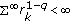 . Then
. Then  is the recessive solution if and only if (2.4) holds.
is the recessive solution if and only if (2.4) holds. is a solution of (2.1) if and only if
is a solution of (2.1) if and only if 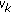 is a solution of
is a solution of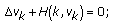
 for
for  with the equality if and only if
with the equality if and only if 
 if and only if
if and only if 
 be a solution of (3.4) and suppose that
be a solution of (3.4) and suppose that  for some
for some 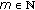 , that is,
, that is,  , then
, then  if and only if
if and only if 