- Research Article
- Open access
- Published:
Permanence of a Discrete  -Species Schoener Competition System with Time Delays and Feedback Controls
-Species Schoener Competition System with Time Delays and Feedback Controls
Advances in Difference Equations volume 2009, Article number: 515706 (2009)
Abstract
A discrete  -species Schoener competition system with time delays and feedback controls is proposed. By applying the comparison theorem of difference equation, sufficient conditions are obtained for the permanence of the system.
-species Schoener competition system with time delays and feedback controls is proposed. By applying the comparison theorem of difference equation, sufficient conditions are obtained for the permanence of the system.
1. Introduction
In 1974, Schoener [1] proposed the following competition model:

where  are all positive constants.
are all positive constants.
May [2] suggested the following set of equations to describe a pair of mutualists:

where  are the densities of the species
are the densities of the species  at time
at time  , respectively.
, respectively.  are positive constants. He showed that system (1.2) has a globally asymptotically stable equilibrium point in the region
are positive constants. He showed that system (1.2) has a globally asymptotically stable equilibrium point in the region  .
.
Both of the above-mentioned works are considered the continuous cases. However, many authors [3–5] have argued that the discrete time models governed by difference equations are more appropriate than the continuous ones when the populations have nonoverlapping generations. Bai et al. [6] argued that the discrete case of cooperative system is more appropriate, and they proposed the following system:

On the other hand, as was pointed out by Huo and Li [7], ecosystem in the real world is continuously disturbed by unpredictable forces which can result in changes in the biological parameters such as survival rates. Practical interest in ecology is the question of whether or not an ecosystem can withstand those unpredictable disturbances which persist for a finite period of time. In the language of control variables, we call the disturbance functions as control variables. During the last decade, many scholars did excellent works on the feedback control ecosystems (see [8–11] and the references cited therein).
Chen [11] considered the permanence of the following nonautonomous discrete N-species cooperation system with time delays and feedback controls of the form

where  is the density of cooperation species
is the density of cooperation species  ,
,  is the control variable ([11] and the references cited therein).
is the control variable ([11] and the references cited therein).
Motivated by the above question, we consider the following discrete  -species Schoener competition system with time delays and feedback controls:
-species Schoener competition system with time delays and feedback controls:

where  is the density of competitive species at
is the density of competitive species at  th generation;
th generation;  is the control variable;
is the control variable;  is the first-order forward difference operator
is the first-order forward difference operator  .
.
Throughout this paper, we assume the following.
 are all bounded nonnegative sequence such that
are all bounded nonnegative sequence such that

Here, for any bounded sequence  ,
, 
 are all nonnegative integers.
are all nonnegative integers.
Let  , we consider (1.5) together with the following initial conditions:
, we consider (1.5) together with the following initial conditions:

It is not difficult to see that solutions of (1.5) and (1.7) are well defined for all  and satisfy
and satisfy

The aim of this paper is, by applying the comparison theorem of difference equation, to obtain a set of sufficient conditions which guarantee the permanence of the system (1.5).
2. Permanence
In this section, we establish a permanence result for system (1.5).
Definition 2.1.
System (1.5) is said to be permanent if there exist positive constants  and
and  such that
such that

for any solution  of system (1.5).
of system (1.5).
Now, let us consider the first-order difference equation

where  are positive constants. Following Lemma
are positive constants. Following Lemma  is a direct corollary of Theorem
is a direct corollary of Theorem  of L. Wang and M. Q. Wang [12, page 125].
of L. Wang and M. Q. Wang [12, page 125].
Lemma 2.2.
Assuming that  , for any initial value y(0), there exists a unique solution y(k) of (2.2) which can be expressed as follow:
, for any initial value y(0), there exists a unique solution y(k) of (2.2) which can be expressed as follow:

where  . Thus, for any solution
. Thus, for any solution  of system (2.2), one has
of system (2.2), one has

Following comparison theorem of difference equation is Theorem  of [12, page 241].
of [12, page 241].
Lemma 2.3.
Let  . For any fixed
. For any fixed  is a nondecreasing function with respect to
is a nondecreasing function with respect to  , and for
, and for  , the following inequalities hold:
, the following inequalities hold:

If  , then
, then  for all
for all  .
.
Now let us consider the following single species discrete model:

where  and
and  are strictly positive sequences of real numbers defined for
are strictly positive sequences of real numbers defined for  and
and  . Similarly to the proof of Propositions
. Similarly to the proof of Propositions  and
and  [13], we can obtain the following.
[13], we can obtain the following.
Lemma 2.4.
Any solution of system (2.6) with initial condition  satisfies
satisfies

where

Proposition 2.5.
Assume that  and
and  hold, then
hold, then

where

Proof.
Let  be any positive solution of system (1.5), from the
be any positive solution of system (1.5), from the  th equation of (1.5), we have
th equation of (1.5), we have

Let  , the inequality above is equivalent to
, the inequality above is equivalent to

Summing both sides of (2.12) from  to
to  leads to
leads to

and so,

therefore,

Substituting (2.15) to the  th equation of (1.5) leads to
th equation of (1.5) leads to

By applying Lemmas 2.3 and 2.4, it immediately follows that

For any positive constant  small enough, it follows from (2.17) that there exists enough large
small enough, it follows from (2.17) that there exists enough large  such that
such that

From the  th equation of the system (1.5) and (2.18), we can obtain
th equation of the system (1.5) and (2.18), we can obtain

for all  . And so,
. And so,

for all  . Noticing that
. Noticing that  , by applying Lemmas 2.2 and 2.3, it follows from (2.20) that
, by applying Lemmas 2.2 and 2.3, it follows from (2.20) that

Setting  in the inequality above leads to
in the inequality above leads to

This completes the proof of Proposition 2.5.
Now we are in the position of stating the permanence of system (1.5).
Theorem 2.6.
Assume that  and
and  hold, assume further that
hold, assume further that

then system (1.5) is permanent.
Proof.
By applying Proposition 2.5, we see that to end the proof of Theorem 2.6, it is enough to show that under the conditions of Theorem 2.6,

From Proposition 2.5, for all  , there exists a
, there exists a  for all
for all  ,
,

From the  th equation of system (1.5) and (2.25), we have
th equation of system (1.5) and (2.25), we have

where

Let  , the inequality above is equivalent to
, the inequality above is equivalent to

Summing both sides of (2.28) from  to
to  leads to
leads to

and so,

where

Therefore,

Substituting (2.32) to the  th equation of (1.5) leads to
th equation of (1.5) leads to

for all  , where
, where

Condition (2.23) shows that Lemma 2.4 could be apply to (2.33), and so, by applying Lemmas 2.3 and 2.4, it immediately follows that

where

Setting  in (2.35) leads to
in (2.35) leads to

where

For any positive constant  small enough, it follows from (2.37) that there exists enough large
small enough, it follows from (2.37) that there exists enough large  such that
such that

From the  th equation of the system (1.5) and (2.39), we can obtain
th equation of the system (1.5) and (2.39), we can obtain

for all  . And so,
. And so,

for all  . Noticing that
. Noticing that  , by applying Lemmas 2.2 and 2.3, it follows from (2.41) that
, by applying Lemmas 2.2 and 2.3, it follows from (2.41) that

Setting  in the inequality above leads to
in the inequality above leads to

This ends the proof of Theorem 2.6.
Now let us consider the following discrete  -species Schoener competition system with time delays:
-species Schoener competition system with time delays:

where  is the density of species
is the density of species  . Obviously, system (2.44) is the generalization of system (1.5). From the previous proof, we can immediately obtain the following theorem.
. Obviously, system (2.44) is the generalization of system (1.5). From the previous proof, we can immediately obtain the following theorem.
Theorem 2.7.
Assume that  and
and  hold, assume further that
hold, assume further that

then system (2.44) is permanent.
References
Chen L, Song X, Lu Z: Mathematical Models and Methods in Ecology. Sichuan Science and Technology Press, Chengdu, China; 2003.
May RM: Theoretical Ecology, Principles and Applications. Sounders, Philadelphia, Pa, USA; 1976.
Agarwal RP: Difference Equations and Inequalities: Theory, Methods, and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Murry JD: Mathematical Biology. Springer, New York, NY, USA; 1989.
Wang W, Lu Z: Global stability of discrete models of Lotka-Volterra type. Nonlinear Analysis: Theory, Methods & Applications 1999,35(7):1019-1030.
Bai L, Fan M, Wang K: Existence of positive periodic solution for difference equations of a cooperative system. Journal of Biomathematics 2004,19(3):271-279.
Huo H-F, Li W-T: Positive periodic solutions of a class of delay differential system with feedback control. Applied Mathematics and Computation 2004,148(1):35-46. 10.1016/S0096-3003(02)00824-X
Chen FD, Chen XX, Cao JD, Chen AP: Positive periodic solutions of a class of non-autonomous single species population model with delays and feedback control. Acta Mathematica Sinica 2005,21(6):1319-1336. 10.1007/s10114-005-0585-6
Chen F: Positive periodic solutions of neutral Lotka-Volterra system with feedback control. Applied Mathematics and Computation 2005,162(3):1279-1302. 10.1016/j.amc.2004.03.009
Chen F: Permanence in nonautonomous multi-species predator-prey system with feedback controls. Applied Mathematics and Computation 2006,173(2):694-709. 10.1016/j.amc.2005.04.047
Chen F:Permanence of a discrete
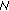 -species cooperation system with time delays and feedback controls. Applied Mathematics and Computation 2007,186(1):23-29. 10.1016/j.amc.2006.07.084
-species cooperation system with time delays and feedback controls. Applied Mathematics and Computation 2007,186(1):23-29. 10.1016/j.amc.2006.07.084Wang L, Wang MQ: Ordinary Difference Equation. Xinjiang University Press, Xinjiang, China; 1991.
Chen F: Permanence and global attractivity of a discrete multispecies Lotka-Volterra competition predator-prey systems. Applied Mathematics and Computation 2006,182(1):3-12. 10.1016/j.amc.2006.03.026
Acknowledgments
This work is supported by the Foundation of Education, Department of Fujian Province (JA05204), and the Foundation of Science and Technology, Department of Fujian Province (2005K027).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, X., Yang, W. Permanence of a Discrete  -Species Schoener Competition System with Time Delays and Feedback Controls.
Adv Differ Equ 2009, 515706 (2009). https://doi.org/10.1155/2009/515706
-Species Schoener Competition System with Time Delays and Feedback Controls.
Adv Differ Equ 2009, 515706 (2009). https://doi.org/10.1155/2009/515706
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/515706
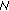 -species cooperation system with time delays and feedback controls. Applied Mathematics and Computation 2007,186(1):23-29. 10.1016/j.amc.2006.07.084
-species cooperation system with time delays and feedback controls. Applied Mathematics and Computation 2007,186(1):23-29. 10.1016/j.amc.2006.07.084