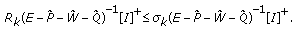- Research Article
- Open access
- Published:
Asymptotic Behavior of Impulsive Infinite Delay Difference Equations with Continuous Variables
Advances in Difference Equations volume 2009, Article number: 495972 (2009)
Abstract
A class of impulsive infinite delay difference equations with continuous variables is considered. By establishing an infinite delay difference inequality with impulsive initial conditions and using the properties of "ϱ-cone," we obtain the attracting and invariant sets of the equations.
1. Introduction
Difference equations with continuous variables are difference equations in which the unknown function is a function of a continuous variable [1]. These equations appear as natural descriptions of observed evolution phenomena in many branches of the natural sciences (see, e.g., [2, 3]). The book mentioned in [3] presents an exposition of some unusual properties of difference equations, specially, of difference equations with continuous variables. In the recent years, the asymptotic behavior and other behavior of delay difference equations with continuous variables have received much attention due to its potential application in various fields such as numerical analysis, control theory, finite mathematics, and computer science. Many results have appeared in the literatures; see, for example, [1, 4–7].
However, besides the delay effect, an impulsive effect likewise exists in a wide variety of evolutionary process, in which states are changed abruptly at certain moments of time. Recently, impulsive difference equations with discrete variable have attracted considerable attention. In particular, delay effect on the asymptotic behavior and other behaviors of impulsive difference equations with discrete variable has been extensively studied by many authors and various results are reported [8–12]. However, to the best of our knowledge, very little has been done with the corresponding problems for impulsive delay difference equations with continuous variables. Motivated by the above discussions, the main aim of this paper is to study the asymptotic behavior of impulsive infinite delay difference equations with continuous variables. By establishing an infinite delay difference inequality with impulsive initial conditions and using the properties of " -cone," we obtain the attracting and invariant sets of the equations.
-cone," we obtain the attracting and invariant sets of the equations.
2. Preliminaries
Consider the impulsive infinite delay difference equation with continuous variable

where  ,
,  ,
,  , and
, and  are real constants,
are real constants,  (here,
(here,  and
and  will be defined later),
will be defined later),  and
and  are positive real numbers.
are positive real numbers.  is an impulsive sequence such that
is an impulsive sequence such that  .
.  ,
,  ,
, , and
, and  :
:  are real-valued functions.
are real-valued functions.
By a solution of (2.1), we mean a piecewise continuous real-valued function  defined on the interval
defined on the interval  which satisfies (2.1) for all
which satisfies (2.1) for all  .
.
In the sequel, by  we will denote the set of all continuous real-valued functions
we will denote the set of all continuous real-valued functions  defined on an interval
defined on an interval  , which satisfies the "compatibility condition"
, which satisfies the "compatibility condition"

By the method of steps, one can easily see that, for any given initial function  , there exists a unique solution
, there exists a unique solution  , of (2.1) which satisfies the initial condition
, of (2.1) which satisfies the initial condition

this function will be called the solution of the initial problem (2.1)–(2.3).
For convenience, we rewrite (2.1) and (2.3) into the following vector form

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  , in which
, in which  .
.
In what follows, we introduce some notations and recall some basic definitions. Let  be the space of
be the space of  -dimensional (nonnegative) real column vectors,
-dimensional (nonnegative) real column vectors,  be the set of
be the set of  (nonnegative) real matrices,
(nonnegative) real matrices,  be the
be the  -dimensional unit matrix, and
-dimensional unit matrix, and  be the Euclidean norm of
be the Euclidean norm of  . For
. For  or
or  ,
,  means that each pair of corresponding elements of
means that each pair of corresponding elements of  and
and  satisfies the inequality "
satisfies the inequality " (
( )."Especially,
)."Especially,  is called a nonnegative matrix if
is called a nonnegative matrix if  , and
, and  is called a positive vector if
is called a positive vector if  .
.  and
and  .
.
 denotes the space of continuous mappings from the topological space
denotes the space of continuous mappings from the topological space  to the topological space
to the topological space  . Especially, let
. Especially, let 

where  is an interval,
is an interval,  and
and  denote the right-hand and left-hand limits of the function
denote the right-hand and left-hand limits of the function  , respectively. Especially, let
, respectively. Especially, let 

For  ,
,  (
( ), and
), and  we define
we define

and  denotes the spectral radius of
denotes the spectral radius of  .
.
For any  or
or  , we always assume that
, we always assume that  is bounded and introduce the following norm:
is bounded and introduce the following norm:

Definition 2.1.
The set  is called a positive invariant set of (2.4), if for any initial value
is called a positive invariant set of (2.4), if for any initial value  , the solution
, the solution  ,
,  .
.
Definition 2.2.
The set  is called a global attracting set of (2.4), if for any initial value
is called a global attracting set of (2.4), if for any initial value  , the solution
, the solution  satisfies
satisfies

where dist ,
,  , for
, for  .
.
Definition 2.3.
System (2.4) is said to be globally exponentially stable if for any solution  , there exist constants
, there exist constants  and
and  such that
such that

If  and
and  , then
, then  .
.
Lemma 2.5 (La Salle [14]).
Suppose that  and
and  , then there exists a positive vector
, then there exists a positive vector  such that
such that  .
.
For  and
and  , we denote
, we denote

which is a nonempty set by Lemma 2.5, satisfying that  for any scalars
for any scalars  ,
,  , and vectors
, and vectors  . So
. So  is a cone without vertex in
is a cone without vertex in  , we call it a "
, we call it a " -cone" [12].
-cone" [12].
3. Main Results
In this section, we will first establish an infinite delay difference inequality with impulsive initial conditions and then give the attracting and invariant sets of (2.4).
Theorem 3.1.
Let  ,
,  , and
, and  , where
, where  . Denote
. Denote  and let
and let  and
and  be a solution of the following infinite delay difference inequality with the initial condition
be a solution of the following infinite delay difference inequality with the initial condition  :
:

-
(a)
Then
 (3.2)
(3.2)
provided the initial conditions

where  and the positive number
and the positive number  is determined by the following inequality:
is determined by the following inequality:

-
(b)
Then
 (3.5)
(3.5)
provided the initial conditions

Proof.
(a): Since  and
and  , then, by Lemma 2.5, there exists a positive vector
, then, by Lemma 2.5, there exists a positive vector  such that
such that  . Using continuity and noting
. Using continuity and noting  , we know that (3.4) has at least one positive solution
, we know that (3.4) has at least one positive solution  , that is,
, that is,

Let  ,
,  , one can get that
, one can get that  , or
, or

To prove (3.2), we first prove, for any given  , when
, when  ,
,

If (3.9) is not true, then there must be a  and some integer
and some integer  such that
such that

By using (3.1), (3.7)–(3.10), and  , we have
, we have

which contradicts the first equality of (3.10), and so (3.9) holds for all  . Letting
. Letting  , then (3.2) holds, and the proof of part (a) is completed.
, then (3.2) holds, and the proof of part (a) is completed.
-
(b)
For any given initial function:
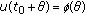 ,
,  , where
, where 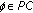 , there is a constant
, there is a constant 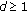 such that
such that  . To prove (3.5), we first prove that
. To prove (3.5), we first prove that 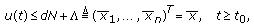 (3.12)
(3.12)
where  (
( small enough), provided that the initial conditions satisfies
small enough), provided that the initial conditions satisfies  .
.
If (3.12) is not true, then there must be a  and some integer
and some integer  such that
such that

By using (3.1), (3.8), (3.13)  , and
, and  , we obtain that
, we obtain that

which contradicts the first equality of (3.13), and so (3.12) holds for all  . Letting
. Letting  , then (3.5) holds, and the proof of part (b) is completed.
, then (3.5) holds, and the proof of part (b) is completed.
Remark 3.2.
Suppose that  in part (a) of Theorem 3.1, then we get [15, Lemma 3].
in part (a) of Theorem 3.1, then we get [15, Lemma 3].
In the following, we will obtain attracting and invariant sets of (2.4) by employing Theorem 3.1. Here, we firstly introduce the following assumptions.
-
(A1) For any
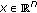 , there exist nonnegative diagonal matrices
, there exist nonnegative diagonal matrices  such that
such that (3.15)
(3.15) -
(A2) For any
 , there exist nonnegative matrices
, there exist nonnegative matrices  such that
such that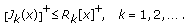 (3.16)
(3.16) -
(A3) Let
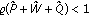 , where
, where (3.17)
(3.17) -
(A4) There exists a constant
 such that
such that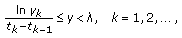 (3.18)
(3.18)where the scalar
 satisfies
satisfies  and is determined by the following inequality
and is determined by the following inequality (3.19)
(3.19)where
 , and
, and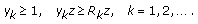 (3.20)
(3.20) -
(A5) Let
 (3.21)
(3.21)where
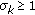 satisfy
satisfy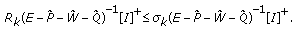 (3.22)
(3.22)
Theorem 3.3.
If ( )–(
)–( ) hold, then
) hold, then  is a global attracting set of (2.4).
is a global attracting set of (2.4).
Proof.
Since  and
and  , then, by Lemma 2.5, there exists a positive vector
, then, by Lemma 2.5, there exists a positive vector  such that
such that  . Using continuity and noting
. Using continuity and noting  , we obtain that inequality (3.19) has at least one positive solution
, we obtain that inequality (3.19) has at least one positive solution  .
.
From (2.4) and condition ( ), we have
), we have

where 
Since  and
and  , then, by Lemma 2.4, we can get
, then, by Lemma 2.4, we can get  , and so
, and so  .
.
For the initial conditions:  ,
,  , where
, where  , we have
, we have

where

By the property of  -cone and
-cone and  , we have
, we have  . Then, all the conditions of part (a) of Theorem 3.1 are satisfied by (3.23), (3.24), and condition
. Then, all the conditions of part (a) of Theorem 3.1 are satisfied by (3.23), (3.24), and condition  , we derive that
, we derive that

Suppose for all  , the inequalities
, the inequalities

hold, where  . Then, from (3.20), (3.22), (3.27), and
. Then, from (3.20), (3.22), (3.27), and  , the impulsive part of (2.4) satisfies that
, the impulsive part of (2.4) satisfies that

This, together with (3.27), leads to

By the property of  -cone again, the vector
-cone again, the vector

On the other hand,

It follows from (3.29)–(3.31) and part (a) of Theorem 3.1 that

By the mathematical induction, we can conclude that

From (3.18) and (3.21),

we can use (3.33) to conclude that

This implies that the conclusion of the theorem holds and the proof is complete.
Theorem 3.4.
If ( )–(
)–( ) with
) with  hold, then
hold, then  is a positive invariant set and also a global attracting set of (2.4).
is a positive invariant set and also a global attracting set of (2.4).
Proof.
For the initial conditions:  ,
,  , where
, where  , we have
, we have

By (3.36) and the part (b) of Theorem 3.1 with  , we have
, we have

Suppose for all  , the inequalities
, the inequalities

hold. Then, from  and
and  , the impulsive part of (2.4) satisfies that
, the impulsive part of (2.4) satisfies that

This, together with (3.36) and (3.38), leads to

It follows from (3.40) and the part (b) of Theorem 3.1 that

By the mathematical induction, we can conclude that

Therefore,  is a positive invariant set. Since
is a positive invariant set. Since  , a direct calculation shows that
, a direct calculation shows that  and
and  in Theorem 3.3. It follows from Theorem 3.3 that the set
in Theorem 3.3. It follows from Theorem 3.3 that the set  is also a global attracting set of (2.4). The proof is complete.
is also a global attracting set of (2.4). The proof is complete.
For the case  , we easily observe that
, we easily observe that  is a solution of (2.4) from
is a solution of (2.4) from  and
and  . In the following, we give the attractivity of the zero solution and the proof is similar to that of Theorem 3.3.
. In the following, we give the attractivity of the zero solution and the proof is similar to that of Theorem 3.3.
Corollary 3.5.
If  hold with
hold with  , then the zero solution of (2.4) is globally exponentially stable.
, then the zero solution of (2.4) is globally exponentially stable.
Remark 3.6.
If  , that is, they have no impulses in (2.4), then by Theorem 3.4, we can obtain the following result.
, that is, they have no impulses in (2.4), then by Theorem 3.4, we can obtain the following result.
Corollary 3.7.
If  and
and  hold, then
hold, then  is a positive invariant set and also a global attracting set of (2.4).
is a positive invariant set and also a global attracting set of (2.4).
4. Illustrative Example
The following illustrative example will demonstrate the effectiveness of our results.
Example 4.1.
Consider the following impulsive infinite delay difference equations:

with

where  and
and  are nonnegative constants, and the impulsive sequence
are nonnegative constants, and the impulsive sequence  satisfies:
satisfies:  . For System (4.1), we have
. For System (4.1), we have  ,
,  . So, it is easy to check that
. So, it is easy to check that  ,
,  , provided that
, provided that  . In this example, we may let
. In this example, we may let  .
.
The parameters of ( )–(
)–( ) are as follows:
) are as follows:

It is easy to prove that  and
and

Let  and
and  which satisfies the inequality
which satisfies the inequality

Let  , then
, then  satisfy
satisfy  ,
, 
Case 1.
Let  ,
,  , and
, and  , then
, then

Moreover,  ,
,  . Clearly, all conditions of Theorem 3.3 are satisfied. So
. Clearly, all conditions of Theorem 3.3 are satisfied. So  is a global attracting set of (4.1).
is a global attracting set of (4.1).
Case 2.
Let  and
and  , then
, then  . Therefore, by Theorem 3.4,
. Therefore, by Theorem 3.4,  is a positive invariant set and also a global attracting set of (4.1).
is a positive invariant set and also a global attracting set of (4.1).
Case 3.
If  and let
and let  and
and  , then
, then

Clearly, all conditions of Corollary 3.5 are satisfied. Therefore, by Corollary 3.5, the zero solution of (4.1) is globally exponentially stable.
References
Philos ChG, Purnaras IK: An asymptotic result for some delay difference equations with continuous variable. Advances in Difference Equations 2004,2004(1):1-10. 10.1155/S1687183904310058
Ladas G: Recent developments in the oscillation of delay difference equations. In Differential Equations (Colorado Springs, CO, 1989), Lecture Notes in Pure and Applied Mathematics. Volume 127. Marcel Dekker, New York, NY, USA; 1991:321-332.
Sharkovsky AN, Maĭstrenko YuL, Romanenko EYu: Difference Equations and Their Applications, Mathematics and Its Applications. Volume 250. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+358.
Deng J: Existence for continuous nonoscillatory solutions of second-order nonlinear difference equations with continuous variable. Mathematical and Computer Modelling 2007,46(5-6):670-679. 10.1016/j.mcm.2006.11.028
Deng J, Xu Z: Bounded continuous nonoscillatory solutions of second-order nonlinear difference equations with continuous variable. Journal of Mathematical Analysis and Applications 2007,333(2):1203-1215. 10.1016/j.jmaa.2006.12.038
Philos ChG, Purnaras IK: On non-autonomous linear difference equations with continuous variable. Journal of Difference Equations and Applications 2006,12(7):651-668. 10.1080/10236190600652360
Philos ChG, Purnaras IK: On the behavior of the solutions to autonomous linear difference equations with continuous variable. Archivum Mathematicum 2007,43(2):133-155.
Li Q, Zhang Z, Guo F, Liu Z, Liang H: Oscillatory criteria for third-order difference equation with impulses. Journal of Computational and Applied Mathematics 2009,225(1):80-86. 10.1016/j.cam.2008.07.002
Peng M: Oscillation criteria for second-order impulsive delay difference equations. Applied Mathematics and Computation 2003,146(1):227-235. 10.1016/S0096-3003(02)00539-8
Yang XS, Cui XZ, Long Y: Existence and global exponential stability of periodic solution of a cellular neural networks difference equation with delays and impulses. Neural Networks. In press
Zhang Q: On a linear delay difference equation with impulses. Annals of Differential Equations 2002,18(2):197-204.
Zhu W, Xu D, Yang Z: Global exponential stability of impulsive delay difference equation. Applied Mathematics and Computation 2006,181(1):65-72. 10.1016/j.amc.2006.01.015
Horn RA, Johnson CR: Matrix Analysis. Cambridge University Press, Cambridge, UK; 1990:xiv+561.
LaSalle JP: The Stability of Dynamical Systems. SIAM, Philadelphia, Pa, USA; 1976:v+76.
Zhu W: Invariant and attracting sets of impulsive delay difference equations with continuous variables. Computers & Mathematics with Applications 2008,55(12):2732-2739. 10.1016/j.camwa.2007.10.020
Acknowledgment
The work is supported by the National Natural Science Foundation of China under Grant 10671133.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ma, Z., Xu, L. Asymptotic Behavior of Impulsive Infinite Delay Difference Equations with Continuous Variables. Adv Differ Equ 2009, 495972 (2009). https://doi.org/10.1155/2009/495972
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/495972


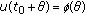 ,
,  , where
, where 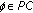 , there is a constant
, there is a constant 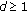 such that
such that  . To prove (3.5), we first prove that
. To prove (3.5), we first prove that 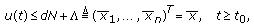
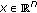 , there exist nonnegative diagonal matrices
, there exist nonnegative diagonal matrices  such that
such that
 , there exist nonnegative matrices
, there exist nonnegative matrices  such that
such that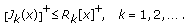
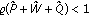 , where
, where
 such that
such that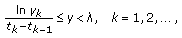
 satisfies
satisfies  and is determined by the following inequality
and is determined by the following inequality
 , and
, and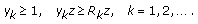

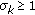 satisfy
satisfy