- Research Article
- Open access
- Published:
On the Nonexistence and Existence of Solutions for a Fourth-Order Discrete Boundary Value Problem
Advances in Difference Equations volume 2009, Article number: 389624 (2009)
Abstract
By using the critical point theory, we establish various sets of sufficient conditions on the nonexistence and existence of solutions for the boundary value problems of a class of fourth-order difference equations.
1. Introduction
In this paper, we denote by  the set of all natural numbers, integers, and real numbers, respectively. For
the set of all natural numbers, integers, and real numbers, respectively. For  , define
, define  when
when  .
.
Consider the following boundary value problem (BVP):

Here,  ,
,  is nonzero and real valued for each
is nonzero and real valued for each  ,
,  is real valued for each
is real valued for each  .
.  is real-valued for each
is real-valued for each  and continuous in the second variable
and continuous in the second variable  .
.  is the forward difference operator defined by
is the forward difference operator defined by  , and
, and  .
.
We may think of (1.1) as being a discrete analogue of the following boundary value problem:

which are used to describe the bending of an elastic beam; see, for example, [1–10] and references therein. Owing to its importance in physics, many methods are applied to study fourth-order boundary value problems by many authors. For example, fixed point theory [1, 3, 5–7], the method of upper and lower solutions [8], and critical point theory [9, 10] are widely used to deal with the existence of solutions for the boundary value problems of fourth-order differential equations.
Because of applications in many areas for difference equations, in recent years, there has been an increased interest in studying of fourth-order difference equation, which include results on periodic solutions [11], results on oscillation [12–14], and results on boundary value problems and other topics [15, 16]. Recently, a few authors have gradually paid attention to applying critical point theory to deal with problems on discrete systems; for example, Yu and Guo in [17] considered the existence of solutions for the following BVP:

The papers [17–20] show that the critical point theory is an effective approach to the study of the boundary value problems of difference equations. In this paper, we will use critical point theory to establish some sufficient conditions on the nonexistence and existence of solutions for the BVP (1.1).
Let

Then the BVP (1.1) becomes

where

The remaining of this paper is organized as follows. First, in Section 2, we give some preliminaries and establish the variational framework for BVP (1.5). Then, in Section 3, we present a sufficient condition on the nonexistence of nontrivial solutions of BVP (1.5). Finally, in Section 4, we provide various sets of sufficient conditions on the existence of solutions of BVP (1.5) when  is superlinear, sublinear, and Lipschitz. Moreover, in a special case of
is superlinear, sublinear, and Lipschitz. Moreover, in a special case of  we obtain a necessary and sufficient condition for the existence of unique solutions of BVP (1.5).
we obtain a necessary and sufficient condition for the existence of unique solutions of BVP (1.5).
To conclude the introduction, we refer to [21, 22] for the general background on difference equations.
2. Preliminaries
In order to apply the critical point theory, we are going to establish the corresponding variational framework of BVP (1.5). First we give some notations.
Let  be the real Euclidean space with dimension
be the real Euclidean space with dimension  . Define the inner product on
. Define the inner product on  as follows:
as follows:

by which the norm  can be induced by
can be induced by

For BVP (1.5), consider the functional  defined on
defined on  as follows:
as follows:

where  is the transpose of a vector in
is the transpose of a vector in  :
:


After a careful computation, we find that the Fréchet derivative of  is
is

where  is defined as
is defined as  .
.
Expanding out  , one can easily see that there is an one-to-one correspondence between the critical point of functional
, one can easily see that there is an one-to-one correspondence between the critical point of functional  and the solution of BVP (1.5). Furthermore,
and the solution of BVP (1.5). Furthermore,  is a critical point of
is a critical point of  if and only if
if and only if  is a solution of BVP (1.5), where
is a solution of BVP (1.5), where  .
.
Therefore, we have reduced the problem of finding a solution of (1.5) to that of seeking a critical point of the functional  defined on
defined on  .
.
In order to obtain the existence of critical points of  on
on  , for the convenience of readers, we cite some basic notations and some known results from critical point theory.
, for the convenience of readers, we cite some basic notations and some known results from critical point theory.
Let  be a real Banach space,
be a real Banach space,  , that is,
, that is,  is a continuously Fréchet differentiable functional defined on
is a continuously Fréchet differentiable functional defined on  , and
, and  is said to satisfy the Palais-Smale condition (P-S condition), if any sequence
is said to satisfy the Palais-Smale condition (P-S condition), if any sequence  for which
for which  is bounded and
is bounded and  as
as  possesses a convergent subsequence in
possesses a convergent subsequence in  .
.
Let  denote the open ball in
denote the open ball in  about
about  of radius
of radius  and let
and let  denote its boundary. The following lemmas are taken from [23, 24] and will play an important role in the proofs of our main results.
denote its boundary. The following lemmas are taken from [23, 24] and will play an important role in the proofs of our main results.
Lemma 2.1 (Linking theorem).
Let  be a real Banach space,
be a real Banach space,  where
where  is a finite-dimensional subspace of
is a finite-dimensional subspace of  . Assume that
. Assume that  satisfies the P-S condition and the following.
satisfies the P-S condition and the following.
-
(F3) There exist constants
 ,
,  such that
such that 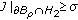 .
. -
(F4) There is an
 and a constant
and a constant  such that
such that  and
and  .
.
Then  possesses a critical value
possesses a critical value  , where
, where

and  , where id denotes the identity operator.
, where id denotes the identity operator.
Lemma 2.2 (Saddle point theorem).
Let  be a real Banach space,
be a real Banach space,  where
where  and is finite-dimensional. Suppose that
and is finite-dimensional. Suppose that  satisfies the P-S condition and the following.
satisfies the P-S condition and the following.
-
(F1) There exist constants
 ,
, 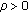 such that
such that 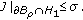
-
(F2) There is
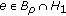 and a constant
and a constant 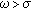 such that
such that 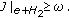
Then  possesses a critical value
possesses a critical value  , where
, where

and  , where id denotes the identity operator.
, where id denotes the identity operator.
Lemma 2.3 (Clark theorem).
Let  be a real Banach space,
be a real Banach space,  with
with  being even, bounded from below, and satisfying P-S condition. Suppose
being even, bounded from below, and satisfying P-S condition. Suppose  , there is a set
, there is a set  such that
such that  is homeomorphic to
is homeomorphic to  (
( dimension unit sphere) by an odd map, and
dimension unit sphere) by an odd map, and  . Then
. Then  has at least
has at least  distinct pairs of nonzero critical points.
distinct pairs of nonzero critical points.
3. Nonexistence of Nontrivial Solutions
In this section, we give a result of nonexistence of nontrivial solutions to BVP (1.5).
Theorem 3.1.
Suppose that matrix  is negative semidefinite and for
is negative semidefinite and for  ,
,

Then BVP (1.5) has no nontrivial solutions.
Proof.
Assume, for the sake of contradiction, that BVP (1.5) has a nontrivial solution. Then  has a nonzero critical point
has a nonzero critical point  . Since
. Since

we get

On the other hand, it follows from (3.1) that

This contradicts with (3.3) and hence the proof is complete.
In the existing literature, results on the nonexistence of solutions of discrete boundary value problems are scarce. Hence Theorem 3.1 complements existing ones.
4. Existence of Solutions
Theorem 3.1 gives a set of sufficient conditions on the nonexistence of solutions of BVP (1.5). In this section, with part of the conditions being violated, we establish the existence of solutions of BVP (1.5) by distinguishing three cases:  is superlinear,
is superlinear,  is sublinear, and
is sublinear, and  is Lipschitzian.
is Lipschitzian.
4.1. The Superlinear Case
In this subsection, we need the following conditions.
-
(P1) For any
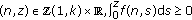 , and
, and 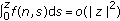 , as
, as 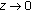 .
. -
(P2) There exist constants
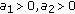 and
and  such that
such that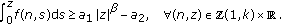 (4.1)
(4.1) -
(P3) Matrix
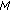 exists at least one positive eigenvalue.
exists at least one positive eigenvalue. -
(P4)
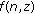 is odd for the second variable
is odd for the second variable  , namely,
, namely,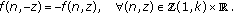 (4.2)
(4.2)
Theorem 4.1.
Suppose that  satisfies
satisfies  . Then BVP (1.5) possesses at least one solution.
. Then BVP (1.5) possesses at least one solution.
Proof.
For any  , we have
, we have

Let  . We have, for any
. We have, for any  ,
,

Since matrix  is symmetric, its all eigenvalues are real. We denote by
is symmetric, its all eigenvalues are real. We denote by  its eigenvalues. Set
its eigenvalues. Set  . Thus for any
. Thus for any  ,
,

The above inequality means that  is coercive. By the continuity of
is coercive. By the continuity of  ,
,  attains its maximum at some point, and we denote it by
attains its maximum at some point, and we denote it by  , that is,
, that is,  , where
, where  . Clearly,
. Clearly,  is a critical point of
is a critical point of  . This completes the proof of Theorem 4.1.
. This completes the proof of Theorem 4.1.
Theorem 4.2.
Suppose that  satisfies the assumptions
satisfies the assumptions  ,
,  and
and  . Then BVP (1.5) possesses at least two nontrivial solutions.
. Then BVP (1.5) possesses at least two nontrivial solutions.
To prove Theorem 4.2, we need the following lemma.
Lemma 4.3.
Assume that  holds, then the functional
holds, then the functional  satisfies the P-S condition.
satisfies the P-S condition.
Proof.
Assume that  is a P-S sequence. Then there exists a constant
is a P-S sequence. Then there exists a constant  such that for any
such that for any  and
and  as
as  . By (4.5) we have
. By (4.5) we have

and so

Due to  , the above inequality means
, the above inequality means  is bounded. Since
is bounded. Since  is a finite-dimensional Hilbert space, there must exist a subsequence of
is a finite-dimensional Hilbert space, there must exist a subsequence of  which is convergent in
which is convergent in  . Therefore, P-S condition is satisfied.
. Therefore, P-S condition is satisfied.
Proof of Theorem 4.2.
Let  ,
,  ,
,  ,
,  be the positive eigenvalues and the negative eigenvalues, where
be the positive eigenvalues and the negative eigenvalues, where  ,
,  . Let
. Let  be an eigenvector of
be an eigenvector of  corresponding to the eigenvalue
corresponding to the eigenvalue  ,
,  , and let
, and let  be an eigenvector of
be an eigenvector of  corresponding to the eigenvalue
corresponding to the eigenvalue  ,
,  , such that
, such that

Let  and
and  be subspaces of
be subspaces of  defined as follows:
defined as follows:

For any 
 , where
, where  . Then
. Then

Let  ,
,  , then
, then  has the following decomposition of direct sum:
has the following decomposition of direct sum:

By assumption  , there exists a constant
, there exists a constant  , such that for any
, such that for any  ,
,  ,
,  . So for any
. So for any  ,
, 

Denote  . Then
. Then

That is to say,  satisfies assumption
satisfies assumption  of Linking theorem.
of Linking theorem.
Take  . For any
. For any  , let
, let  , because
, because  , where
, where  . Then
. Then

Set  and
and  Then
Then  . Furthermore,
. Furthermore,  and
and  are bounded from above. Accordingly, there is some
are bounded from above. Accordingly, there is some  , such that for any
, such that for any  , where
, where  . By Linking theorem,
. By Linking theorem,  possesses a critical value
possesses a critical value  , where
, where

Let  be a critical point corresponding to the critical value
be a critical point corresponding to the critical value  of
of  , that is,
, that is,  . Clearly,
. Clearly,  since
since  . On the other hand, by Theorem 4.1,
. On the other hand, by Theorem 4.1,  has a critical point
has a critical point  satisfying
satisfying  . If
. If  , then Theorem 4.2 holds. Otherwise,
, then Theorem 4.2 holds. Otherwise,  . Then
. Then  , which is the same as
, which is the same as  .
.
Choosing  , we have
, we have  . Because the choice of
. Because the choice of  is arbitrary, we can take
is arbitrary, we can take  . Similarly, there exists a positive number
. Similarly, there exists a positive number  , for any
, for any  , where
, where  . Again, by the Linking theorem,
. Again, by the Linking theorem,  possesses a critical value
possesses a critical value  , where
, where

If  , then the proof is complete. Otherwise
, then the proof is complete. Otherwise  . Because
. Because  and
and  , then
, then  attains its maximum at some point in the interior of sets
attains its maximum at some point in the interior of sets  and
and  . But
. But  , and
, and  for
for  . Thus there is a critical point
. Thus there is a critical point  satisfying
satisfying  ,
,  .
.
The proof of Theorem 4.2 is now complete.
Theorem 4.4.
Suppose that  satisfies the assumptions
satisfies the assumptions  ,
,  ,
,  and
and  . Then BVP (1.5) possesses at least
. Then BVP (1.5) possesses at least  distinct pairs of nontrivial solutions, where
distinct pairs of nontrivial solutions, where  is the dimension of the space spanned by the eigenvectors corresponding to the positive eigenvalues of
is the dimension of the space spanned by the eigenvectors corresponding to the positive eigenvalues of  .
.
Proof.
From the proof of Theorem 4.2, it is easy to know that  is bounded from above and satisfies the P-S condition. It is clear that
is bounded from above and satisfies the P-S condition. It is clear that  is even and
is even and  , and we should find a set
, and we should find a set  and an odd map such that
and an odd map such that  is homeomorphic to
is homeomorphic to  by an odd map.
by an odd map.
We take  where
where  and
and  are defined as in the proof of Theorem 4.2. It is clear that
are defined as in the proof of Theorem 4.2. It is clear that  is homeomorphic to
is homeomorphic to  (
( dimension unit sphere) by an odd map. With (4.13), we get
dimension unit sphere) by an odd map. With (4.13), we get  . Thus all the conditions of Lemma 2.3 are satisfied, and
. Thus all the conditions of Lemma 2.3 are satisfied, and  has at least
has at least  distinct pairs of nonzero critical points. Consequently, BVP (1.5) possesses at least
distinct pairs of nonzero critical points. Consequently, BVP (1.5) possesses at least  distinct pairs nontrivial solutions. The proof of Theorem 4.4 is complete.
distinct pairs nontrivial solutions. The proof of Theorem 4.4 is complete.
4.2. The Sublinear Case
In this subsection, we will consider the case where  is sublinear. First, we assume the following.
is sublinear. First, we assume the following.
 There exist constants
There exist constants  and
and  such that
such that

The first result is as follows.
Theorem 4.5.
Suppose that  is satisfied and that matrix M is positive definite. Then BVP (1.5) possesses at least one solution.
is satisfied and that matrix M is positive definite. Then BVP (1.5) possesses at least one solution.
Proof.
The proof will be finished when the existence of one critical point of functional  defined as in (2.3) is proved.
defined as in (2.3) is proved.
Assume that matrix  is positive definite. We denote by
is positive definite. We denote by  its eigenvalues, where
its eigenvalues, where  . Then for any
. Then for any  , followed by
, followed by  we have
we have

By the continuity of  on
on  , the above inequality means that there exists a lower bound of values of functional
, the above inequality means that there exists a lower bound of values of functional  . Classical calculus shows that
. Classical calculus shows that  attains its minimal value at some point, and then there exist
attains its minimal value at some point, and then there exist  such that
such that  . Clearly,
. Clearly,  is a critical point of the functional
is a critical point of the functional  .
.
Corollary 4.6.
Suppose that matrix M is positive definite, and  satisfies that there exist constants
satisfies that there exist constants  ,
,  and
and  such that
such that

Then BVP (1.5) possesses at least one solution.
Corollary 4.7.
Suppose that matrix M is positive definite, and  satisfies the following.
satisfies the following.
 There exists a constant
There exists a constant  such that for any
such that for any  ,
,  .
.
Then BVP (1.5) possesses at least one solution.
Proof.
Assume that matrix  is positive definite. In this case, for any
is positive definite. In this case, for any  ,
,

Since the rest of the proof is similar to Theorem 4.5, we do not repeat them here.
When  is neither positive definite nor negative definite, we now assume that
is neither positive definite nor negative definite, we now assume that  is nonsingular, and we have the following result.
is nonsingular, and we have the following result.
Theorem 4.8.
Suppose that  is nonsingular,
is nonsingular,  satisfies
satisfies  . Then BVP (1.5) possesses at least one solution.
. Then BVP (1.5) possesses at least one solution.
Proof.
We may assume that  is neither positive definite nor negative definite. Let
is neither positive definite nor negative definite. Let  ,
,  denote all eigenvalues of
denote all eigenvalues of  , where
, where  and
and  . For any
. For any  , let
, let  be an eigenvector of
be an eigenvector of  corresponding to the eigenvalue
corresponding to the eigenvalue  ,
,  , such that
, such that

Let  and
and  be subspaces of
be subspaces of  defined as follows:
defined as follows:

Then  has the following decomposition of direct sum:
has the following decomposition of direct sum:

Let  be defined as in (2.3). Then
be defined as in (2.3). Then  . By (4.20),
. By (4.20),

Suppose that  is a P-S sequence. Then there exists a constant
is a P-S sequence. Then there exists a constant  such that for any
such that for any  ,
,  and
and  as
as  . Thus, for sufficiently large
. Thus, for sufficiently large  and for any
and for any  , we have
, we have  .
.
Let  . We have, by (2.6), for any
. We have, by (2.6), for any  ,
,

Thus for sufficiently large  , we get
, we get

Thus,

which implies that  is bounded.
is bounded.
Now we are going to prove that  is also bounded. By (4.25),
is also bounded. By (4.25),

Thus we have

And so

Due to  is bounded. Then
is bounded. Then  is bounded. Since
is bounded. Since  is a finite-dimensional Hilbert space, there must exist a subsequence of
is a finite-dimensional Hilbert space, there must exist a subsequence of  which is convergent in
which is convergent in  . Therefore, P-S condition is satisfied.
. Therefore, P-S condition is satisfied.
In order to apply the saddle point theorem to prove the conclusion, we consider the functional  and verify the conditions of Lemma 2.2.
and verify the conditions of Lemma 2.2.
For any  ,
,  , we have
, we have

This implies that  is true.
is true.
For any  ,
,  ,
,

This implies that  is true.
is true.
So far we have verified all the assumptions of Lemma 2.2 and hence  has at least a critical point in
has at least a critical point in  . This completes the proof.
. This completes the proof.
Consider the following special case

Here,

It can be verified that  is positive definite, then we have the following corollaries.
is positive definite, then we have the following corollaries.
Corollary 4.9.
Suppose that there exist constants  and
and  such that
such that

Then BVP (4.33) possesses at least one solution.
Corollary 4.10.
Suppose that  satisfies
satisfies  . Then BVP (4.33) possesses at least one solution.
. Then BVP (4.33) possesses at least one solution.
4.3. The Lipschitz Case
In this subsection, we suppose the following.
 Assume that there exist positive constants
Assume that there exist positive constants  ,
,  such that for any
such that for any  ,
,

When  is Lipschitzian in the second variable
is Lipschitzian in the second variable  , namely, there exists a constant
, namely, there exists a constant  such that for any
such that for any  ,
,  ,
,  ,
,

then condition (4.36) is satisfied.
Theorem 4.11.
Suppose that  is satisfied and M is nonsingular. If
is satisfied and M is nonsingular. If  , where
, where  and
and  are the minimal positive eigenvalue and maximal negative eigenvalue of
are the minimal positive eigenvalue and maximal negative eigenvalue of  , respectively, then BVP (1.5) possesses at least one solution.
, respectively, then BVP (1.5) possesses at least one solution.
Proof.
Assume that  is a P-S sequence. Then
is a P-S sequence. Then  as
as  . Thus for sufficiently large
. Thus for sufficiently large  , we get
, we get  . Since
. Since  , then for sufficiently large
, then for sufficiently large  ,
,

In view of (4.36), we have

It follows, by using the inequality  for
for  and Hölder's inequality, that
and Hölder's inequality, that

By a similar argument to the proof of Theorem 4.8, we can decompose  into the following form of direct sum:
into the following form of direct sum:

where  and
and  can be referred to (4.22). Thus
can be referred to (4.22). Thus  can be expressed by
can be expressed by

and  , where
, where  . Therefore,
. Therefore,

Hence,

By the fact that  , we know that the sequence
, we know that the sequence  is bounded and therefore the P-S condition is verified.
is bounded and therefore the P-S condition is verified.
Now we are going to check conditions  and
and  for functional
for functional  . In fact, by (4.36), we have for any
. In fact, by (4.36), we have for any  ,
,

Thus, for any  ,
,  ,
,

for some positive constant  .
.
For any  ,
,  , we have
, we have

Until now, we have verified all the assumptions of Lemma 2.2 and hence  has at least a critical point in
has at least a critical point in  . This completes the proof.
. This completes the proof.
Finally, we consider the special case that  is independent of the second variable
is independent of the second variable  ; that is,
; that is,  for any
for any  , the BVP (1.1) becomes
, the BVP (1.1) becomes

As in Section 2, we reduce the existence of solutions of BVP (4.48) to the existence of critical points of a functional  defined on
defined on  as follows:
as follows:

where  is defined as in (2.4), and
is defined as in (2.4), and  . Then we can see that the critical point of
. Then we can see that the critical point of  is just the solution to the following system of linear algebraic equations:
is just the solution to the following system of linear algebraic equations:

By using the theory of linear algebra, we have the next necessary and sufficient conditions.
Theorem 4.12.
-
(i)
BVP (4.48) has at least one solution if and only if
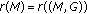 , where
, where 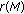 denotes the rank of matrix
denotes the rank of matrix  and
and 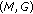 is the augmented matrix defined as follows:
is the augmented matrix defined as follows:  (4.51)
(4.51) -
(ii)
BVP (4.48) has a unique solution if and only if
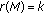 .
.
References
Aftabizadeh AR: Existence and uniqueness theorems for fourth-order boundary value problems. Journal of Mathematical Analysis and Applications 1986,116(2):415-426. 10.1016/S0022-247X(86)80006-3
Gupta CP: Existence and uniqueness theorems for the bending of an elastic beam equation. Applicable Analysis 1988,26(4):289-304. 10.1080/00036818808839715
Agarwal RP: On fourth order boundary value problems arising in beam analysis. Differential and Integral Equations 1989,2(1):91-110.
Gupta CP: Existence and uniqueness theorems for some fourth order fully quasilinear boundary value problems. Applicable Analysis 1990,36(3-4):157-169. 10.1080/00036819008839930
Ma R, Wang H: On the existence of positive solutions of fourth-order ordinary differential equations. Applicable Analysis 1995,59(1–4):225-231.
Bai Z, Wang H: On positive solutions of some nonlinear fourth-order beam equations. Journal of Mathematical Analysis and Applications 2002,270(2):357-368. 10.1016/S0022-247X(02)00071-9
Yao Q: Positive solutions of a nonlinear elastic beam equation rigidly fastened on the left and simply supported on the right. Nonlinear Analysis: Theory, Methods & Applications 2008,69(5-6):1570-1580. 10.1016/j.na.2007.07.002
Ruyun M, Jihui Z, Shengmao F: The method of lower and upper solutions for fourth-order two-point boundary value problems. Journal of Mathematical Analysis and Applications 1997,215(2):415-422. 10.1006/jmaa.1997.5639
Li F, Zhang Q, Liang Z: Existence and multiplicity of solutions of a kind of fourth-order boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2005,62(5):803-816. 10.1016/j.na.2005.03.054
Han G, Xu Z: Multiple solutions of some nonlinear fourth-order beam equations. Nonlinear Analysis: Theory, Methods & Applications 2008,68(12):3646-3656. 10.1016/j.na.2007.04.007
Cai X, Yu J, Guo Z: Existence of periodic solutions for fourth-order difference equations. Computers & Mathematics with Applications 2005,50(1-2):49-55. 10.1016/j.camwa.2005.03.004
Agarwal RP, Grace SR, Manojlovic JV: On the oscillatory properties of certain fourth order nonlinear difference equations. Journal of Mathematical Analysis and Applications 2006,322(2):930-956. 10.1016/j.jmaa.2005.09.059
Thandapani E, Arockiasamy IM: Fourth-order nonlinear oscillations of difference equations. Computers & Mathematics with Applications 2001,42(3–5):357-368.
Schmeidel E, Szmanda B: Oscillatory and asymptotic behavior of certain difference equation. Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4731-4742. 10.1016/S0362-546X(01)00585-5
He Z, Yu J: On the existence of positive solutions of fourth-order difference equations. Applied Mathematics and Computation 2005,161(1):139-148. 10.1016/j.amc.2003.12.016
Zhang B, Kong L, Sun Y, Deng X: Existence of positive solutions for BVPs of fourth-order difference equations. Applied Mathematics and Computation 2002,131(2-3):583-591. 10.1016/S0096-3003(01)00171-0
Yu J, Guo Z: On boundary value problems for a discrete generalized Emden-Fowler equation. Journal of Differential Equations 2006,231(1):18-31. 10.1016/j.jde.2006.08.011
Jiang L, Zhou Z:Three solutions to Dirichlet boundary value problems for
 -Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.
-Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.Jiang L, Zhou Z: Multiple nontrivial solutions for a class of higher dimensional discrete boundary value problems. Applied Mathematics and Computation 2008,203(1):30-38. 10.1016/j.amc.2007.12.014
Bai D, Xu Y: Nontrivial solutions of boundary value problems of second-order difference equations. Journal of Mathematical Analysis and Applications 2007,326(1):297-302. 10.1016/j.jmaa.2006.02.091
Agarwal RP: Difference Equations and Inequalities: Theory, Methods, and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Elaydi SN: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. Springer, New York, NY, USA; 1996:xiv+389.
Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics. Volume 65. American Mathematical Society, Providence, RI, USA; 1986:viii+100.
Chang KC: Critical Point Theory and Its Applications. Science and Technical Press, Shanghai, China; 1986:iv+316.
Acknowledgment
This work is supported by the Specialized Fund for the Doctoral Program of Higher Eduction (no. 20071078001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Huang, S., Zhou, Z. On the Nonexistence and Existence of Solutions for a Fourth-Order Discrete Boundary Value Problem. Adv Differ Equ 2009, 389624 (2009). https://doi.org/10.1155/2009/389624
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/389624
 ,
,  such that
such that 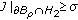 .
. and a constant
and a constant  such that
such that  and
and  .
. ,
, 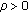 such that
such that 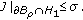
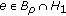 and a constant
and a constant 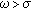 such that
such that 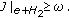
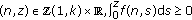 , and
, and 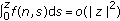 , as
, as 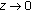 .
.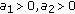 and
and  such that
such that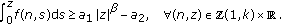
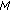 exists at least one positive eigenvalue.
exists at least one positive eigenvalue.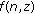 is odd for the second variable
is odd for the second variable  , namely,
, namely,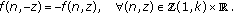
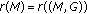 , where
, where 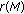 denotes the rank of matrix
denotes the rank of matrix  and
and 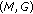 is the augmented matrix defined as follows:
is the augmented matrix defined as follows: 
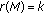 .
. -Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.
-Laplacian difference equations. Advances in Difference Equations 2008, 2008:-10.