- Research Article
- Open access
- Published:
Permanence and Stable Periodic Solution for a Discrete Competitive System with Multidelays
Advances in Difference Equations volume 2009, Article number: 375486 (2010)
Abstract
The permanence and the existence of periodic solution for a discrete nonautonomous competitive system with multidelays are considered. Also the stability of the periodic solution is discussed. Numerical examples are given to confirm the theoretical results.
1. Introduction
In this paper, we consider the permanence and the periodic solution for the following discrete competitive model with  -species and several delays:
-species and several delays:

In model (1.1),  is the population density of the species
is the population density of the species  at n th time step (year, month, day),
at n th time step (year, month, day),  represents the intrinsic growth rate of species
represents the intrinsic growth rate of species  at n th time step, and
at n th time step, and  reflects the interspecific or intraspecific competitive intensity of species
reflects the interspecific or intraspecific competitive intensity of species  to species
to species  with time delay
with time delay  at n th time step.
at n th time step.
As a special case of model (1.1), the following discrete model

has been investigated as the discrete analogue of the well-known continuous Logistic model [1–4]:

And many complex dynamics, such as periodic cycles and chaotic behavior, were found in model (1.2) [2, 4, 5].
It is well known that the reproduction rate and the carrying capacity are intensively influenced by the environment; therefore the following model with time varying coefficients

was developed from model (1.2) and has been studied recently in [6].
An equivalent version of model (1.4) can be written as

Models (1.2), (1.4), and (1.5) are both considering of ecosystems for single-species. As a result of coupling  equations both described by model (1.5), one can write out the following model for
equations both described by model (1.5), one can write out the following model for  -species:
-species:

If  (
( ) is nonnegative sequences, model (1.6) represents the competitive ecosystem of Lotka-Volterra type with
) is nonnegative sequences, model (1.6) represents the competitive ecosystem of Lotka-Volterra type with  -species [7]. When
-species [7]. When  , model (1.6) was introduced in [8] and recently has been studied in [9]. The autonomous case of (1.6) when
, model (1.6) was introduced in [8] and recently has been studied in [9]. The autonomous case of (1.6) when  has been studied in [10] and the following permanent result was obtained [10, Theorem 2].
has been studied in [10] and the following permanent result was obtained [10, Theorem 2].
Lemma 1.1.
If  , then (1.6) is permanent.
, then (1.6) is permanent.
It is well known that the effect of time delay plays an important role in population dynamics [11]; therefore, model (1.1) can be constructed from model (1.6) while considering the effect of time delays. Obviously, models (1.2), (1.4), and (1.5) are special cases of model (1.1) for single-species. Model (1.6) is also special case of model (1.1) without delays. Some aspects of model (1.1) has been discussed in the literature. For example, the global asymptotical stability of (1.1) with  and the permanence of (1.1) with
and the permanence of (1.1) with  were investigated in [12]. Necessary and sufficient conditions for the permanence of the autonomous case of (1.1) with two-species
were investigated in [12]. Necessary and sufficient conditions for the permanence of the autonomous case of (1.1) with two-species

were obtained in [13].
In theoretical population dynamics, it is important whether or not all species in multispecies ecosystem can be permanent [14, 15]. Many permanent or persistent results have been obtained for continuous biomathematical models that are governed by differential equation(s). For example, one can refer to [11, 16–21] and references cited therein. However, permanent results on the delayed discrete-time competitive model of Lotka-Volterra type are rarely few [13, 22], especially with  -species (
-species ( ). In this manuscript, first we will obtain new sufficient conditions for the permanence of (1.1) when
). In this manuscript, first we will obtain new sufficient conditions for the permanence of (1.1) when  .
.
The population densities observed in the field are usually oscillatory. What cause such phenomenon is a purpose to model population interactions [9, 23]. We will further investigate the existence and stability of the periodic solution for model (1.1) under the assumption that the coefficients of model (1.1) are all periodic with a common period.
The results obtained in this paper are complements to those related with model (1.1). We give some examples to show that the results here are not enclosed by other earlier works. The paper is organized as follows. In next section, we give some preliminaries and obtain the sufficient conditions which guarantee the permanence of model (1.1). In Section 3, we prove the existence of the positive periodic solution of model (1.1) and obtain the sufficient conditions for the stability of the periodic solution.
2. Preliminaries and Permanence
Due to the biological backgrounds of model (1.1), throughout this paper we make the following basic assumptions.
-
(H1)
 and
and  (
(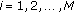 ) are sequences bounded from below and from above by positive constants.
) are sequences bounded from below and from above by positive constants. -
(H2)
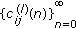 (
(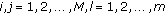 ) and
) and  (
(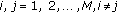 ) are nonnegative and bounded sequences.
) are nonnegative and bounded sequences. -
(H3)
The initial values are given by
 .
.
Next we give some definitions that will be be used in this paper. We write  and
and  ,
,  .
.
Definition 2.1.
We say that  is a solution of (1.1) with initial values (
is a solution of (1.1) with initial values ( ) if
) if  satisfies (1.1) for
satisfies (1.1) for  and
and  .
.
Under assumptions ( ), (
), ( ), and (
), and ( ), solutions of model (1.1) are all consisting of positive sequences; such solution will be called positive solution of (1.1).
), solutions of model (1.1) are all consisting of positive sequences; such solution will be called positive solution of (1.1).
Definition 2.2.
Model (1.1) is said to be permanent if there are positive constants  and
and  such that
such that

for each positive solution  of model (1.1).
of model (1.1).
Definition 2.3.
System (1.1) is strongly persistent if each positive solution  of (1.1) satisfies
of (1.1) satisfies

Definition 2.4.
If each positive solution  of model (1.1) satisfies that
of model (1.1) satisfies that  as
as  , we say that the solution
, we say that the solution  of (1.1) is globally attractive or globally stable, where
of (1.1) is globally attractive or globally stable, where  is the maximum norm of the Banach space
is the maximum norm of the Banach space  .
.
From Definitions 2.2 and 2.3, we know that model (1.1) is strongly persistent if model (1.1) is permanent. For the sake of simplicity, we introduce the following notations for any sequences  :
:

Next we will discuss the sufficient conditions which guarantee that system (1.1) with initial conditions ( ) is permanent. In the following, we denote
) is permanent. In the following, we denote  as the solutions of system (1.1) with initial conditions (
as the solutions of system (1.1) with initial conditions ( ). Clearly,
). Clearly,  is positive sequence.
is positive sequence.
Lemma 2.5.
If  satisfies
satisfies

for  , where
, where  is a positive sequence bounded from below and from above by positive constants and
is a positive sequence bounded from below and from above by positive constants and  is a positive integer, then there exists positive constant
is a positive integer, then there exists positive constant  such that
such that

and  .
.
Proof.
The proof of this lemma is similar to that of Lemma 1 in [24]; we omit the details.
Lemma 2.6.
If  satisfies
satisfies

for  , where
, where  and
and  are positive sequences bounded from below and from above by positive constants,
are positive sequences bounded from below and from above by positive constants,  is a positive integer and
is a positive integer and  . Further, assume that
. Further, assume that  and
and  , then
, then

Proof.
The proof of this lemma is similar to that of Lemma 2 in [24]; we omit the details.
In the following, we denote

Theorem 2.7.
Assume that

then model (1.1) is permanent.
Proof.
From model (1.1), we have

for  . Therefore, by Lemma 2.5 there exists positive constants
. Therefore, by Lemma 2.5 there exists positive constants  such that
such that

Hence,

for all large  and
and  (
( ). By Lemma 2.6,
). By Lemma 2.6,  (
( ) provided that
) provided that

where  is a positive constant. Note that
is a positive constant. Note that  for
for  , then
, then

That is, (2.13) is satisfied if (2.9) holds. Moreover, if (2.9) holds, then  and
and  (
( ).
).
Next we give an example to show the feasibility of the conditions of Theorem 2.7. This example also shows that Theorem 2.7 is not enclosed by other related works.
Example 2.8.
Let us consider the following competitive model:

where  ,
,  ,
,  .
.
From (2.15),  ,
,  , and hence, (2.9) is satisfied. According to Theorem 2.7, system (2.15) is permanent (see Figure 1).
, and hence, (2.9) is satisfied. According to Theorem 2.7, system (2.15) is permanent (see Figure 1).
Remark 2.9.
The permanence of system (2.15) was also investigated in [12]. But our conditions which guarantee the permanence of (2.15) are different from that of [12, Lemma 5]. Adopting the same notations as [12, Lemma 5], we have  ,
,  , and
, and  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . But
. But  ,
,  ; that is, the assumptions
; that is, the assumptions  and
and  of [12, Lemma 5] are not satisfied. Therefore, the permanence of system (2.15) cannot be obtained by [12, Lemma 5].
of [12, Lemma 5] are not satisfied. Therefore, the permanence of system (2.15) cannot be obtained by [12, Lemma 5].
Remark 2.10.
The global asymptotical stability of model (1.1) is studied in [12] under the assumption that model (1.1) is strongly persistent. But the authors of [12] did not discuss the strong persistence of model (1.1) with  -species (
-species ( ). Theorem 2.7 in this paper gives sufficient conditions which guarantee the strong persistence of model (1.1).
). Theorem 2.7 in this paper gives sufficient conditions which guarantee the strong persistence of model (1.1).
3. Periodic Solution
In this section, we assume that the coefficients of model (1.1) are periodic with common period  , that is,
, that is,

The aim of this section is to show the existence of positive periodic solution of model (1.1) under assumption (3.1) and further find additional conditions for the global stability of this positive periodic solution.
Theorem 3.1.
Let the assumptions of Theorem 2.7 and (3.1) be satisfied; then there exists a positive periodic solution of model (1.1) with the period  .
.
Proof.
Model (1.1) is permanent by Theorem 2.7. Therefore, model (1.1) is point dissipative. It follows from [25, Theorem 4.3] that there exists a positive periodic solution of model (1.1). Note (3.1), and the coefficients of model (1.1) are all  -periodic. Therefore, this solution is
-periodic. Therefore, this solution is  -periodic.
-periodic.
Example 3.2.
Consider the following model:

Direct computation shows that the coefficients of model (3.2) satisfy the assumptions of Theorem 2.7. The coefficients of model (3.2) are all periodic with the common period 20. Hence, model (3.2) has a positive periodic solution by Theorem 3.1 (see Figures 2 and 3). Figures 4 and 5 show that the period of the sequences  or
or  is 20, respectively. More precisely, the values of sequence
is 20, respectively. More precisely, the values of sequence  within a period are 0.7330, 0.7358, 0.7383, 0.7403, 0.7415, 0.7419, 0.7413, 0.7399, 0.7377, 0.7351, 0.7323, 0.7295, 0.7271, 0.7252, 0.7241, 0.7238, 0.7243, 0.7257, 0.7277, and 0.7302, respectively. The values of sequence
within a period are 0.7330, 0.7358, 0.7383, 0.7403, 0.7415, 0.7419, 0.7413, 0.7399, 0.7377, 0.7351, 0.7323, 0.7295, 0.7271, 0.7252, 0.7241, 0.7238, 0.7243, 0.7257, 0.7277, and 0.7302, respectively. The values of sequence  within a period are 0.3869, 0.3846, 0.3821, 0.3796, 0.3775, 0.3759, 0.3750, 0.3749, 0.3756, 0.3770, 0.3790, 0.3813, 0.3838, 0.3862, 0.3882, 0.3898, 0.3907, 0.3908, 0.3902, and 0.3889, respectively.
within a period are 0.3869, 0.3846, 0.3821, 0.3796, 0.3775, 0.3759, 0.3750, 0.3749, 0.3756, 0.3770, 0.3790, 0.3813, 0.3838, 0.3862, 0.3882, 0.3898, 0.3907, 0.3908, 0.3902, and 0.3889, respectively.
Next, we study the global stability of the positive periodic solution obtained in Theorem 3.1.
Theorem 3.3.
Let the assumptions of Theorem 3.1 be satisfied; further, assume that

i  , then for every positive solution
, then for every positive solution  of model (1.1), one has
of model (1.1), one has

where  is the positive periodic solution obtained in Theorem 3.1.
is the positive periodic solution obtained in Theorem 3.1.
Proof.
Let

where  ) is the positive periodic solution of model (1.1). Model (1.1) can be rewritten as
) is the positive periodic solution of model (1.1). Model (1.1) can be rewritten as

Therefore,

where  ,
,  ,
,  ,
,  .
.
In view of (3.3), we can choose  such that
such that

And from Theorem 2.7, there exists a positive integer  such that
such that

for  and
and  given as above (
given as above ( ,
,  ).
).
Notice that  lies between
lies between  and
and  , and
, and  lies between
lies between  and
and  (
( ,
,  ), from (3.7), we have
), from (3.7), we have

for  and
and  .
.
Denote

We have  . Notice that
. Notice that  is arbitrarily given; from (3.10), we get
is arbitrarily given; from (3.10), we get

Therefore,

That is,

and (3.4) follows consequently.
References
Kocic VK, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993.
May RM: Nonlinear problems in ecology. In Chaotic Behavior of Deterministic Systems. Edited by: Iooss G, Helleman R, Stora R. North-Holland, Amsterdam, The Netherlands; 1983:515–563.
Lakshmikantham V, Trigiante D: Theory of Difference Equations: Numerical Methods and Applications, Mathematics in Science and Engineering. Volume 181. Academic Press, Boston, Mass, USA; 1988:x+242.
Hastings A: Population Biology: Concepts and Models. Springer, New York, NY, USA; 1996.
Goh BS: Management and Analysis of Biological Populations. Elsevier, Amsterdam, The Netherlands; 1980.
Zhou Z, Zou X: Stable periodic solutions in a discrete periodic logistic equation. Applied Mathematics Letters 2003,16(2):165–171. 10.1016/S0893-9659(03)80027-7
Wang W, Lu Z: Global stability of discrete models of Lotka-Volterra type. Nonlinear Analysis: Theory, Methods & Applications 1999,35(8):1019–1030. 10.1016/S0362-546X(98)00112-6
May RM: Biological populations with nonoverlapping generations: stable points, stable cycles, and chaos. Science 1974,186(4164):645–647. 10.1126/science.186.4164.645
Chen Y, Zhou Z: Stable periodic solution of a discrete periodic Lotka-Volterra competition system. Journal of Mathematical Analysis and Applications 2003,277(1):358–366. 10.1016/S0022-247X(02)00611-X
Lu Z, Wang W: Permanence and global attractivity for Lotka-Volterra difference systems. Journal of Mathematical Biology 1999,39(3):269–282. 10.1007/s002850050171
Kuang Y: Delay Differential Equations with Applications in Population Dynamics, Mathematics in Science and Engineering. Volume 191. Academic Press, Boston, Mass, USA; 1993:xii+398.
Wang W, Mulone G, Salemi F, Salone V: Global stability of discrete population models with time delays and fluctuating environment. Journal of Mathematical Analysis and Applications 2001,264(1):147–167. 10.1006/jmaa.2001.7666
Saito Y, Ma W, Hara T: A necessary and sufficient condition for permanence of a Lotka-Volterra discrete system with delays. Journal of Mathematical Analysis and Applications 2001,256(1):162–174. 10.1006/jmaa.2000.7303
Hutson V, Schmitt K: Permanence and the dynamics of biological systems. Mathematical Biosciences 1992,111(1):1–71. 10.1016/0025-5564(92)90078-B
Jansen VAA, Sigmund K: Shaken not stirred: on permanence in ecological communities. Theoretical Population Biology 1998,54(3):195–201. 10.1006/tpbi.1998.1384
Freedman HI, Ruan SG: Uniform persistence in functional-differential equations. Journal of Differential Equations 1995,115(1):173–192. 10.1006/jdeq.1995.1011
Hofbauer J, Kon R, Saito Y: Qualitative permanence of Lotka-Volterra equations. Journal of Mathematical Biology 2008,57(6):863–881. 10.1007/s00285-008-0192-0
Cui J, Takeuchi Y, Lin Z: Permanence and extinction for dispersal population systems. Journal of Mathematical Analysis and Applications 2004,298(1):73–93. 10.1016/j.jmaa.2004.02.059
Takeuchi Y, Cui J, Miyazaki R, Saito Y: Permanence of delayed population model with dispersal loss. Mathematical Biosciences 2006,201(1–2):143–156. 10.1016/j.mbs.2005.12.012
Zhang L, Teng Z: Permanence for a delayed periodic predator-prey model with prey dispersal in multi-patches and predator density-independent. Journal of Mathematical Analysis and Applications 2008,338(1):175–193. 10.1016/j.jmaa.2007.05.016
Allen LJS: Persistence and extinction in single-species reaction-diffusion models. Bulletin of Mathematical Biology 1983,45(2):209–227.
Muroya Y: Global attractivity for discrete models of nonautonomous logistic equations. Computers & Mathematics with Applications 2007,53(7):1059–1073. 10.1016/j.camwa.2006.12.010
Itokazu T, Hamaya Y: Almost periodic solutions of prey-predator discrete models with delay. Advances in Difference Equations 2009, 2009:-19.
Yang X: Uniform persistence and periodic solutions for a discrete predator-prey system with delays. Journal of Mathematical Analysis and Applications 2006,316(1):161–177. 10.1016/j.jmaa.2005.04.036
Hale J: Theory of Functional Differential Equations, Applied Mathematical Sciences. 2nd edition. Springer, New York, NY, USA; 1977:x+365.
Acknowledgments
The research is supported by the foundation of Jiangsu Polytechnic University (ZMF09020020). The author would like to thank the editor Professor Jianshe Yu and the referees for their helpful comments and suggestions which greatly improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, C. Permanence and Stable Periodic Solution for a Discrete Competitive System with Multidelays. Adv Differ Equ 2009, 375486 (2010). https://doi.org/10.1155/2009/375486
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/375486
 and
and  (
(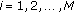 ) are sequences bounded from below and from above by positive constants.
) are sequences bounded from below and from above by positive constants.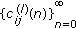 (
(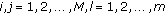 ) and
) and  (
(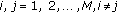 ) are nonnegative and bounded sequences.
) are nonnegative and bounded sequences. .
.



 : the coefficients are given in Example 3.2.
: the coefficients are given in Example 3.2.
 : the coefficients are given in Example 3.2.
: the coefficients are given in Example 3.2.