- Research Article
- Open access
- Published:
Dynamics for Nonlinear Difference Equation 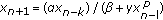
Advances in Difference Equations volume 2009, Article number: 235691 (2009)
Abstract
We mainly study the global behavior of the nonlinear difference equation in the title, that is, the global asymptotical stability of zero equilibrium, the existence of unbounded solutions, the existence of period two solutions, the existence of oscillatory solutions, the existence, and asymptotic behavior of non-oscillatory solutions of the equation. Our results extend and generalize the known ones.
1. Introduction
Consider the following higher order difference equation:

where  , the parameters
, the parameters  and
and  are nonnegative real numbers and the initial conditions
are nonnegative real numbers and the initial conditions  and
and  are nonnegative real numbers such that
are nonnegative real numbers such that

It is easy to see that if one of the parameters  is zero, then the equation is linear. If
is zero, then the equation is linear. If  , then (1.1) can be reduced to a linear one by the change of variables
, then (1.1) can be reduced to a linear one by the change of variables  . So in the sequel we always assume that the parameters
. So in the sequel we always assume that the parameters  and
and  are positive real numbers.
are positive real numbers.
The change of variables  reduces (1.1) into the following equation:
reduces (1.1) into the following equation:

where  .
.
Note that  is always an equilibrium point of (1.3). When
is always an equilibrium point of (1.3). When  , (1.3) also possesses the unique positive equilibrium
, (1.3) also possesses the unique positive equilibrium  .
.
The linearized equation of (1.3) about the equilibrium point  is
is

so, the characteristic equation of (1.3) about the equilibrium point  is either, for
is either, for  ,
,

or, for 

The linearized equation of (1.3) about the positive equilibrium point  has the form
has the form

with the characteristic equation either, for  ,
,

or, for 

When  ,
,  , (1.1) has been investigated in [1–4]. When
, (1.1) has been investigated in [1–4]. When  ,
,  , (1.1) reduces to the following form:
, (1.1) reduces to the following form:

El-Owaidy et al. [3] investigated the global asymptotical stability of zero equilibrium, the periodic character and the existence of unbounded solutions of (1.10).
On the other hand, when  , (1.1) is just the discrete delay logistic model investigated in [4,
, (1.1) is just the discrete delay logistic model investigated in [4,  ]. Therefore, it is both theoretically and practically meaningful to study (1.1).
]. Therefore, it is both theoretically and practically meaningful to study (1.1).
Our aim in this paper is to extend and generalize the work in [3]. That is, we will investigate the global behavior of (1.1), including the global asymptotical stability of zero equilibrium, the existence of unbounded solutions, the existence of period two solutions, the existence of oscillatory solutions, the existence and asymptotic behavior of nonoscillatory solutions of the equation. Our results extend and generalize the corresponding ones of [3].
For the sake of convenience, we now present some definitions and known facts, which will be useful in the sequel.
Consider the difference equation

where  is a positive integer, and the function
is a positive integer, and the function  has continuous partial derivatives.
has continuous partial derivatives.
A point  is called an equilibrium of (1.11) if
is called an equilibrium of (1.11) if

That is,  for
for  is a solution of (1.11), or equivalently,
is a solution of (1.11), or equivalently,  is a fixed point of
is a fixed point of  .
.
The linearized equation of (1.11) associated with the equilibrium point  is
is

We need the following lemma.
-
(i)
If all the roots of the polynomial equation

lie in the open unit disk  , then the equilibrium
, then the equilibrium  of (1.11) is locally asymptotically stable.
of (1.11) is locally asymptotically stable.
-
(ii)
If at least one root of (1.11) has absolute value greater than one, then the equilibrium
 of (1.11) is unstable.
of (1.11) is unstable.
For the related investigations for nonlinear difference equations, see also [7–11] and the references cited therein.
2. Global Asymptotic Stability of Zero Equilibrium
In this section, we investigate global asymptotic stability of zero equilibrium of (1.3). We first have the following results.
Lemma 2.1.
The following statements are true.
(a)If  , then the equilibrium point
, then the equilibrium point  of (1.3) is locally asymptotically stable.
of (1.3) is locally asymptotically stable.
(b)If  , then the equilibrium point
, then the equilibrium point  of (1.3) is unstable. Moreover, for
of (1.3) is unstable. Moreover, for  , (1.3) has a
, (1.3) has a  -dimension local stable manifold and a
-dimension local stable manifold and a  -dimension local unstable manifold.
-dimension local unstable manifold.
(c)If  ,
,  is odd and
is odd and  is even, then the positive equilibrium point
is even, then the positive equilibrium point  of (1.3) is unstable.
of (1.3) is unstable.
Proof.
-
(a)
When
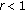 , it is clear from (1.5) and (1.6) that every characteristic root
, it is clear from (1.5) and (1.6) that every characteristic root 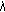 satisfies
satisfies 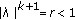 or
or 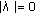 , and so, by Lemma 1.1(i),
, and so, by Lemma 1.1(i), 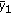 is locally asymptotically stable.
is locally asymptotically stable. -
(b)
When
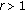 , if
, if 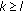 , then it is clear from (1.5) that every characteristic root
, then it is clear from (1.5) that every characteristic root 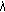 satisfies
satisfies 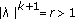 , and so, by Lemma 1.1(ii),
, and so, by Lemma 1.1(ii),  is unstable. If
is unstable. If  , then (1.6) has
, then (1.6) has 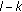 characteristic roots
characteristic roots 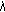 satisfying
satisfying 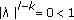 , which corresponds to a
, which corresponds to a 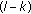 -dimension local stable manifold of (1.3), and
-dimension local stable manifold of (1.3), and 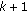 characteristic roots
characteristic roots  satisfying
satisfying 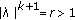 , which corresponds to a
, which corresponds to a  -dimension local unstable manifold of (1.3).
-dimension local unstable manifold of (1.3). -
(c)
If
 is odd and
is odd and  is even, then, regardless of
is even, then, regardless of 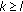 or
or  , correspondingly, the characteristic equation (1.8) or (1.9) always has one characteristic root
, correspondingly, the characteristic equation (1.8) or (1.9) always has one characteristic root 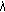 lying the interval
lying the interval  . It follows from Lemma 1.1(ii) that
. It follows from Lemma 1.1(ii) that 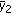 is unstable.
is unstable.
Remark 2.2.
Lemma 2.1(a) includes and improves [3, Theorem 3.1(i)]. Lemma 2.1(b) and (c) include and generalize [3, Theorem 3.1(ii) and (iii)], respectively.
Now we state the main results in this section.
Theorem 2.3.
Assume that  , then the equilibrium point
, then the equilibrium point  of (1.3) is globally asymptotically stable.
of (1.3) is globally asymptotically stable.
Proof.
We know from Lemma 2.1 that the equilibrium point  of (1.3) is locally asymptotically stable. It suffices to show that
of (1.3) is locally asymptotically stable. It suffices to show that  for any nonnegative solution
for any nonnegative solution  of (1.3).
of (1.3).
Since

 converges for any
converges for any  . Let
. Let  , then
, then

Thereout, one has

that is,

which implies  . The proof is over.
. The proof is over.
Remark 2.4.
Theorem 2.3 includes [3, Theorem 3.3].
3. Existence of Eventual Period Two Solution
In this section, one studies the eventual nonnegative prime period two solutions of (1.3). A solution  of (1.3) is said to be eventual prime periodic two solution if there exists an
of (1.3) is said to be eventual prime periodic two solution if there exists an 
 such that
such that  for
for  and
and  holds for all
holds for all  .
.
Theorem 3.1.
-
(a)
Assume
 is odd and
is odd and  is even, then (1.3) possesses eventual prime period two solutions if and only if
is even, then (1.3) possesses eventual prime period two solutions if and only if 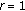 .
. -
(b)
Assume
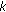 is odd and
is odd and  is odd, then (1.3) possesses eventual prime period two solutions if and only if
is odd, then (1.3) possesses eventual prime period two solutions if and only if 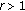 .
. -
(c)
Assume
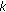 is even and
is even and  is even. Then the necessary condition for (1.3) to possess eventual prime period two solutions is
is even. Then the necessary condition for (1.3) to possess eventual prime period two solutions is  and
and  .
. -
(d)
Assume
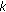 is even and
is even and  is odd. Then, (1.3) has no eventual prime period two solutions.
is odd. Then, (1.3) has no eventual prime period two solutions.
Proof.
-
(a)
If (1.3) has the eventual nonnegative prime period two solution

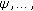 then, we eventually have
then, we eventually have  and
and 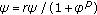 . Hence,
. Hence,

If  , then we can derive from (3.1) that
, then we can derive from (3.1) that  if
if  or vice versa, which contradicts the assumption that
or vice versa, which contradicts the assumption that 
 is the eventual prime period two solution of (1.3). So,
is the eventual prime period two solution of (1.3). So,  . Accordingly,
. Accordingly,  and
and  , which indicate that
, which indicate that  when
when  or that
or that  and
and  do not exist when
do not exist when  , which are also impossible. Therefore,
, which are also impossible. Therefore,  .
.
Conversely, if  , then choose the initial conditions such as
, then choose the initial conditions such as  and
and  , or such as
, or such as  and
and  . We can see by induction that
. We can see by induction that  is the prime period two solution of (1.3).
is the prime period two solution of (1.3).
-
(b)
Let
 be the eventual prime period two solution of (1.3), then, it holds eventually that
be the eventual prime period two solution of (1.3), then, it holds eventually that 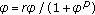 and
and 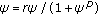 . Hence,
. Hence,

If  , then
, then  . This is impossible. So
. This is impossible. So  . Moreover,
. Moreover,  and
and  or
or  and
and  , that is,
, that is,  is the prime period two solution of (1.3).
is the prime period two solution of (1.3).
-
(c)
Assume that (1.3) has the eventual nonnegative prime period two solution

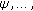 then eventually
then eventually

Obviously,  implies
implies  or vice versa. This is impossible. So
or vice versa. This is impossible. So  . It is easy to see from (3.3) that
. It is easy to see from (3.3) that  and
and  satisfy the equation
satisfy the equation

that is,  and
and  are two distinct positive roots of
are two distinct positive roots of  . From (3.4) we can see that
. From (3.4) we can see that  does not have two distinct positive roots at all when
does not have two distinct positive roots at all when  , alternatively, (1.3) does not have the nonnegative prime period two solution at all when
, alternatively, (1.3) does not have the nonnegative prime period two solution at all when  . Therefore, we assume
. Therefore, we assume  in the following.
in the following.
Let  in (3.4), then the equation
in (3.4), then the equation  has at least two distinct positive roots.
has at least two distinct positive roots.
By simple calculation, one has

If  , we can see
, we can see  for all
for all  . This means that
. This means that  is strictly increasing in the interval
is strictly increasing in the interval  and hence the equation,
and hence the equation,  cannot have two distinct positive roots. So, next we consider
cannot have two distinct positive roots. So, next we consider  , which implies
, which implies  . Denote
. Denote  . We need to discuss several cases, respectively, as follows.
. We need to discuss several cases, respectively, as follows.
Case 1.
It holds that  . Then
. Then  for all
for all  , hence,
, hence,  is convex. Again,
is convex. Again,  . So it is impossible for
. So it is impossible for  to have two distinct positive roots.
to have two distinct positive roots.
Case 2.
It holds that  and
and  . Then, for
. Then, for  ,
,  and so
and so  ; for
; for  ,
,  and so
and so  . At this time, one always has
. At this time, one always has  . Then
. Then  cannot have two distinct positive roots.
cannot have two distinct positive roots.
Case 3.
It holds that  ,
,  and
and  . Then, for
. Then, for  ,
,  and so
and so  and hence
and hence  , that is,
, that is,  has no solutions for
has no solutions for  ; for
; for  ,
,  , that is,
, that is,  is convex for
is convex for  . Noticing
. Noticing  , it is also impossible for
, it is also impossible for  to have two distinct positive roots for
to have two distinct positive roots for  .
.
Case 4.
It holds that  ,
,  and
and  . This is only case where
. This is only case where  could have two distinct positive roots, which implies
could have two distinct positive roots, which implies  and
and  .
.
-
(d)
Let …, φ, ψ, φ, ψ,… be the eventual nonnegative prime period two solution of (1.3), then, it is eventually true that

It is easy to see that  and
and  . So, we have
. So, we have

that is,  and
and  are two distinct positive roots of
are two distinct positive roots of  . Obviously, when
. Obviously, when  , the
, the  has no positive roots.
has no positive roots.
Now let  and set
and set  . Then the function,
. Then the function,  has at least two distinct positive roots. However,
has at least two distinct positive roots. However,  for any
for any  , which indicates that
, which indicates that  is strictly increasing in the interval
is strictly increasing in the interval  . This implies that the function
. This implies that the function  does not have two distinct positive roots at all in the interval
does not have two distinct positive roots at all in the interval  . In turn, (1.3) does not have the prime period two solution when
. In turn, (1.3) does not have the prime period two solution when  .
.
4. Existence of Oscillatory Solution
For the oscillatory solution of (1.3), we have the following results.
Theorem 4.1.
Assume  ,
,  is odd and
is odd and  is even. Then, there exist solutions
is even. Then, there exist solutions  of (1.3) which oscillate about
of (1.3) which oscillate about  with semicycles of length one.
with semicycles of length one.
Proof.
We only prove the case where  (the proof of the case where
(the proof of the case where  is similar and will be omitted). Choose the initial values of (1.3) such that
is similar and will be omitted). Choose the initial values of (1.3) such that

or

We will only prove the case where (4.1) holds. The case where (4.2) holds is similar and will be omitted. According to (1.3), one can see that

So, the proof follows by induction.
5. Existence of Unbounded Solution
With respect to the unbounded solutions of (1.3), the following results are derived.
Theorem 5.1.
Assume  ,
,  is odd, and
is odd, and  is even, then (1.3) possesses unbounded solutions.
is even, then (1.3) possesses unbounded solutions.
Proof.
We only prove the case where  (the proof of the case where
(the proof of the case where  is similar and will be omitted). Choose the initial values of (1.3) such that
is similar and will be omitted). Choose the initial values of (1.3) such that

In the following, assume  . From the proof of Theorem 4.1, one can see that
. From the proof of Theorem 4.1, one can see that  when
when  is odd and that
is odd and that  for
for  even. Together with
even. Together with

It is derived that

So,  is decreasing for
is decreasing for  odd whereas
odd whereas  is increasing for
is increasing for  even. Let
even. Let

then one has
(1) for
for  odd and
odd and  for
for  even,
even,
(2) .
.
Now, either  for some even
for some even  in which case the proof is complete, or
in which case the proof is complete, or  for all even
for all even  . We shall prove that this latter is impossible. In fact, we prove that
. We shall prove that this latter is impossible. In fact, we prove that  for all even
for all even  .
.
Assume  for some even
for some even  , then one has, by (5.2),
, then one has, by (5.2),  . Noticing (1), one hence further gets
. Noticing (1), one hence further gets  . However
. However  is odd, according to (1),
is odd, according to (1),  . This is a contradiction.
. This is a contradiction.
Therefore,  for any even
for any even  . Accordingly,
. Accordingly,  are unbounded subsequences of this solution
are unbounded subsequences of this solution  of (1.3) for even
of (1.3) for even  . Simultaneously, for odd
. Simultaneously, for odd  , we get
, we get

The proof is complete.
Remark 5.2.
Theorem 5.1 includes and generalizes [3, Theorem 3.5].
6. Existence and Asymptotic Behavior of Nonoscillatory Solution
In this section, we consider the existence and asymptotic behavior of nonoscillatory solution of (1.3). Because all solutions of (1.3) are nonnegative, relative to the zero equilibrium point  , every solution of (1.3) is a positive semicycle, a trivial nonoscillatory solution! Thus, it suffices to consider the positive equilibrium
, every solution of (1.3) is a positive semicycle, a trivial nonoscillatory solution! Thus, it suffices to consider the positive equilibrium  when studying the nonoscillatory solutions of (1.3). At this time,
when studying the nonoscillatory solutions of (1.3). At this time,  .
.
Firstly, we have the following results.
Theorem 6.1.
Every nonoscillatory solution of (1.3) with respect to  approaches
approaches  .
.
Proof.
Let  be any one nonoscillatory solution of (1.3) with respect to
be any one nonoscillatory solution of (1.3) with respect to  . Then, there exists an
. Then, there exists an  such that
such that

or

We only prove the case where (6.1) holds. The proof for the case where (6.2) holds is similar and will be omitted. According to (6.1), for  , one has
, one has

So,  is decreasing for
is decreasing for  with upper bound
with upper bound  . Hence,
. Hence,  exists and is finite. Denote
exists and is finite. Denote

Then  . Taking limits on both sides of (1.3), we can derive
. Taking limits on both sides of (1.3), we can derive

which shows  and completes this proof.
and completes this proof.
A problem naturally arises: are there nonoscillatory solutions of (1.3)? Next, we will positively answer this question. Our result is as follows.
Theorem 6.2.
However (1.3) possesses asymptotic solutions with a single semicycle (positive semicycle or negative semicycle).
The main tool to prove this theorem is to make use of Berg' inclusion theorem [12]. Now, for the sake of convenience of statement, we first state some preliminaries. For this, refer also to [13]. Consider a general real nonlinear difference equation of order  with the form
with the form

where  ,
,  . Let
. Let  and
and  be two sequences satisfying
be two sequences satisfying  and
and  as
as  . Then (maybe under certain additional conditions), for any given
. Then (maybe under certain additional conditions), for any given  , there exist a solution
, there exist a solution  of (6.6) and an
of (6.6) and an  such
such

Denote

which is called an asymptotic stripe. So, if  , then it is implied that there exists a real sequence
, then it is implied that there exists a real sequence  such that
such that  and
and  for
for  .
.
We now state the inclusion theorem [12].
Lemma 6.3.
Let  be continuously differentiable when
be continuously differentiable when  , for
, for  , and
, and  . Let the partial derivatives of
. Let the partial derivatives of  satisfy
satisfy

as  uniformly in
uniformly in  for
for  ,
,  , as far as
, as far as  . Assume that there exist a sequence
. Assume that there exist a sequence  and constants
and constants  such that
such that

for  as
as  , and suppose there exists an integer
, and suppose there exists an integer  , with
, with  , such that
, such that

Then, for sufficiently large  , there exists a solution
, there exists a solution  of (6.6) satisfying (6.7).
of (6.6) satisfying (6.7).
Proof of Theorem 6.2.
We only prove the case where  (the proof of the case where
(the proof of the case where  is similar and will be omitted). Put
is similar and will be omitted). Put  (
( is denoted into
is denoted into  for short). Then (1.3) is transformed into
for short). Then (1.3) is transformed into

An approximate equation of (6.12) is

provided that  as
as  . The general solution of (6.13) is
. The general solution of (6.13) is

where  and
and  are the
are the  roots of the polynomial
roots of the polynomial

Obviously,  . So,
. So,  has a positive root
has a positive root  lying in the interval (0, 1). Now, choose the solution
lying in the interval (0, 1). Now, choose the solution  for this
for this  . For some
. For some  , define the sequences
, define the sequences  and
and  , respectively, as follows:
, respectively, as follows:

Obviously,  and
and  as
as  .
.
Now, define again the function

Then the partial derivatives of  w.r.t.
w.r.t.  , respectively, are
, respectively, are

When  ,
,  . So,
. So,  ,
,  , as
, as  uniformly in
uniformly in  for
for  ,
,  .
.
Moreover, from the definition of the function  and (6.17) and (6.18), after some calculation, we find
and (6.17) and (6.18), after some calculation, we find

Now choose  . Noting
. Noting

we have  Again,
Again,

where

Therefore, one has

Up to here, all conditions of Lemma 6.3 with  and
and  are satisfied. Accordingly, we see that, for arbitrary
are satisfied. Accordingly, we see that, for arbitrary  and for sufficiently large
and for sufficiently large  , say
, say  , (6.12) has a solution
, (6.12) has a solution  in the stripe
in the stripe  , where
, where  and
and  are as defined in (6.16). Because
are as defined in (6.16). Because  ,
,  for
for  . Thus, (1.3) has a solution
. Thus, (1.3) has a solution  satisfying
satisfying  for
for  . Since (1.3) is an autonomous equation,
. Since (1.3) is an autonomous equation,  still is its solution, which evidently satisfies
still is its solution, which evidently satisfies  for
for  . Therefore, the proof is complete.
. Therefore, the proof is complete.
Remark 6.4.
If we take  in (6.16), then
in (6.16), then  . At this time, (1.3) possesses solutions
. At this time, (1.3) possesses solutions  which remain below its equilibrium for all
which remain below its equilibrium for all  , that is, (1.3) has solutions with a single negative semicycle.
, that is, (1.3) has solutions with a single negative semicycle.
Remark 6.5.
The appropriate equation (6.12) is just the linearized equation of (1.3) associated with  .
.
Remark 6.6.
The existence and asymptotic behavior of nonoscillatory solution of special cases of (1.3) has not been found to be considered in the known literatures.
References
Kulenović MRS, Ladas G: Dynamics of Second Order Rational Difference Equations with Open Problems and Conjecture. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002.
Amleh AM, Kirk V, Ladas G: On the dynamics of . Mathematical Sciences Research Hot-Line 2001,5(7):1–15.
El-Owaidy HM, Ahmed AM, Youssef AM: The dynamics of the recursive sequence . Applied Mathematics Letters 2005,18(9):1013–1018. 10.1016/j.aml.2003.09.014
Kocić VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and Its Applications. Volume 256. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993.
Agarwal RP: Difference Equations and Inequalities. 1st edition. Marcel Dekker, New York, NY, USA; 1992.
Agarwal RP: Difference Equations and Inequalities. 2nd edition. Marcel Dekker, New York, NY, USA; 2000.
Su Y-H, Li W-T: Global attractivity of a higher order nonlinear difference equation. Journal of Difference Equations and Applications 2005,11(10):947–958. 10.1080/10236190500273333
Li X: The rule of trajectory structure and global asymptotic stability for a nonlinear difference equation. Indian Journal of Pure and Applied Mathematics 2007,38(6):1–9.
Li X, Agarwal RP: The rule of trajectory structure and global asymptotic stability for a fourth-order rational difference equation. Journal of the Korean Mathematical Society 2007,44(4):787–797. 10.4134/JKMS.2007.44.4.787
Li X, Zhu D, Jin Y: Some properties of a kind of Lyness equations. Chinese Journal of Contemporary Mathematics 2004,24(2):147–155.
Li X, Zhu D: Qualitative analysis of Bobwhite Quail population model. Acta Mathematica Scientia 2003,23(1):46–52.
Berg L: Inclusion theorems for non-linear difference equations with applications. Journal of Difference Equations and Applications 2004,10(4):399–408. 10.1080/10236190310001625280
Li X: Existence of solutions with a single semicycle for a general second-order rational difference equation. Journal of Mathematical Analysis and Applications 2007,334(1):528–533. 10.1016/j.jmaa.2006.12.072
Acknowledgments
This work of the second author is partly supported by NNSF of China (Grant: 10771094) and the Foundation for the Innovation Group of Shenzhen University (Grant: 000133). Y. Wang work is supported by School Foundation of JiangSu Polytechnic University(Grant: JS200801).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, D., Li, X. & Wang, Y. Dynamics for Nonlinear Difference Equation  .
Adv Differ Equ 2009, 235691 (2009). https://doi.org/10.1155/2009/235691
.
Adv Differ Equ 2009, 235691 (2009). https://doi.org/10.1155/2009/235691
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/235691
 of (1.11) is unstable.
of (1.11) is unstable.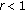 , it is clear from (1.5) and (1.6) that every characteristic root
, it is clear from (1.5) and (1.6) that every characteristic root 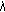 satisfies
satisfies 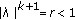 or
or 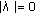 , and so, by Lemma 1.1(i),
, and so, by Lemma 1.1(i), 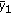 is locally asymptotically stable.
is locally asymptotically stable.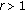 , if
, if 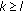 , then it is clear from (1.5) that every characteristic root
, then it is clear from (1.5) that every characteristic root 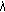 satisfies
satisfies 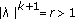 , and so, by Lemma 1.1(ii),
, and so, by Lemma 1.1(ii),  is unstable. If
is unstable. If  , then (1.6) has
, then (1.6) has 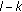 characteristic roots
characteristic roots 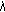 satisfying
satisfying 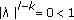 , which corresponds to a
, which corresponds to a 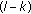 -dimension local stable manifold of (1.3), and
-dimension local stable manifold of (1.3), and 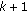 characteristic roots
characteristic roots  satisfying
satisfying 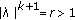 , which corresponds to a
, which corresponds to a  -dimension local unstable manifold of (1.3).
-dimension local unstable manifold of (1.3). is odd and
is odd and  is even, then, regardless of
is even, then, regardless of 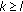 or
or  , correspondingly, the characteristic equation (
, correspondingly, the characteristic equation (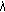 lying the interval
lying the interval  . It follows from Lemma 1.1(ii) that
. It follows from Lemma 1.1(ii) that 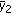 is unstable.
is unstable. is odd and
is odd and  is even, then (1.3) possesses eventual prime period two solutions if and only if
is even, then (1.3) possesses eventual prime period two solutions if and only if 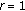 .
.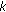 is odd and
is odd and  is odd, then (1.3) possesses eventual prime period two solutions if and only if
is odd, then (1.3) possesses eventual prime period two solutions if and only if 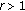 .
.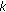 is even and
is even and  is even. Then the necessary condition for (1.3) to possess eventual prime period two solutions is
is even. Then the necessary condition for (1.3) to possess eventual prime period two solutions is  and
and  .
.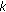 is even and
is even and  is odd. Then, (1.3) has no eventual prime period two solutions.
is odd. Then, (1.3) has no eventual prime period two solutions.
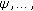 then, we eventually have
then, we eventually have  and
and 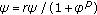 . Hence,
. Hence, be the eventual prime period two solution of (1.3), then, it holds eventually that
be the eventual prime period two solution of (1.3), then, it holds eventually that 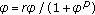 and
and 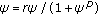 . Hence,
. Hence,
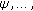 then eventually
then eventually