- Research Article
- Open access
- Published:
Existence of Solutions for Nonlinear Four-Point  -Laplacian Boundary Value Problems on Time Scales
-Laplacian Boundary Value Problems on Time Scales
Advances in Difference Equations volume 2009, Article number: 123565 (2009)
Abstract
We are concerned with proving the existence of positive solutions of a nonlinear second-order four-point boundary value problem with a  -Laplacian operator on time scales. The proofs are based on the fixed point theorems concerning cones in a Banach space. Existence result for
-Laplacian operator on time scales. The proofs are based on the fixed point theorems concerning cones in a Banach space. Existence result for  -Laplacian boundary value problem is also given by the monotone method.
-Laplacian boundary value problem is also given by the monotone method.
1. Introduction
Let  be any time scale such that
be any time scale such that  be subset of
be subset of  . The concept of dynamic equations on time scales can build bridges between differential and difference equations. This concept not only gives us unified approach to study the boundary value problems on discrete intervals with uniform step size and real intervals but also gives an extended approach to study on discrete case with non uniform step size or combination of real and discrete intervals. Some basic definitions and theorems on time scales can be found in [1, 2].
. The concept of dynamic equations on time scales can build bridges between differential and difference equations. This concept not only gives us unified approach to study the boundary value problems on discrete intervals with uniform step size and real intervals but also gives an extended approach to study on discrete case with non uniform step size or combination of real and discrete intervals. Some basic definitions and theorems on time scales can be found in [1, 2].
In this paper, we study the existence of positive solutions for the following nonlinear four-point boundary value problem with a  -Laplacian operator:
-Laplacian operator:


where  is an operator, that is,
is an operator, that is,  for
for  ,
,  where
where  ,
,  ,
,  ,
,  with
with  :
:
-
(H1)
the function
 ,
, -
(H2)
the function
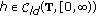 and does not vanish identically on any closed subinterval of
and does not vanish identically on any closed subinterval of 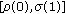 and
and  ,
, -
(H3)
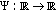 is continuous and satisfies that there exist
is continuous and satisfies that there exist 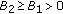 such that
such that 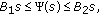 for
for 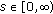 .
.
In recent years, the existence of positive solutions for nonlinear boundary value problems with  -Laplacians has received wide attention, since it has led to several important mathematical and physical applications [3, 4]. In particular, for
-Laplacians has received wide attention, since it has led to several important mathematical and physical applications [3, 4]. In particular, for  or
or  is linear, the existence of positive solutions for nonlinear singular boundary value problems has been obtained [5, 6].
is linear, the existence of positive solutions for nonlinear singular boundary value problems has been obtained [5, 6].  -Laplacian problems with two-, three-, and m-point boundary conditions for ordinary differential equations and difference equations have been studied in [7–9] and the references therein. Recently, there is much attention paid to question of positive solutions of boundary value problems for second-order dynamic equations on time scales, see [10–13]. In particular, we would like to mention some results of Agarwal and O'Regan [14], Chyan and Henderson [5], Song and Weng [15], Sun and Li [16], and Liu [17], which motivate us to consider the
-Laplacian problems with two-, three-, and m-point boundary conditions for ordinary differential equations and difference equations have been studied in [7–9] and the references therein. Recently, there is much attention paid to question of positive solutions of boundary value problems for second-order dynamic equations on time scales, see [10–13]. In particular, we would like to mention some results of Agarwal and O'Regan [14], Chyan and Henderson [5], Song and Weng [15], Sun and Li [16], and Liu [17], which motivate us to consider the  -Laplacian boundary value problem on time scales.
-Laplacian boundary value problem on time scales.
The aim of this paper is to establish some simple criterions for the existence of positive solutions of the  -Laplacian BVP (1.1)-(1.2). This paper is organized as follows. In Section 2 we first present the solution and some properties of the solution of the linear
-Laplacian BVP (1.1)-(1.2). This paper is organized as follows. In Section 2 we first present the solution and some properties of the solution of the linear  -Laplacian BVP corresponding to (1.1)-(1.2). Consequently we define the Banach space, cone and the integral operator to prove the existence of the solution of (1.1)-(1.2). In Section 3, we state the fixed point theorems in order to prove the main results and we get the existence of at least one and two positive solutions for nonlinear
-Laplacian BVP corresponding to (1.1)-(1.2). Consequently we define the Banach space, cone and the integral operator to prove the existence of the solution of (1.1)-(1.2). In Section 3, we state the fixed point theorems in order to prove the main results and we get the existence of at least one and two positive solutions for nonlinear  -Laplacian BVP (1.1)-(1.2). Finally, using the monotone method, we prove the existence of solutions for
-Laplacian BVP (1.1)-(1.2). Finally, using the monotone method, we prove the existence of solutions for  -Laplacian BVP in Section 4.
-Laplacian BVP in Section 4.
2. Preliminaries and Lemmas
In this section, we will give several fixed point theorems to prove existence of positive solutions of nonlinear  -Laplacian BVP (1.1)-(1.2). Also, to state the main results in this paper, we employ the following lemmas. These lemmas are based on the linear dynamic equation:
-Laplacian BVP (1.1)-(1.2). Also, to state the main results in this paper, we employ the following lemmas. These lemmas are based on the linear dynamic equation:

Lemma 2.1.
Suppose condition (H2) holds, then there exists a constant  that satisfies
that satisfies

Furthermore, the function

is a positive continuous function, therefore,  has a minimum on
has a minimum on  , hence one supposes that there exists
, hence one supposes that there exists  such that
such that  for
for  .
.
Proof.
It is easily seen that  is continuous on
is continuous on  .
.
Let

Then, from condition (H2), we have that the function  is strictly monoton nondecreasing on
is strictly monoton nondecreasing on  and
and  , the function
, the function  is strictly monoton nonincreasing on
is strictly monoton nonincreasing on  and
and  , which implies
, which implies 
Throughout this paper, let  , then
, then  is a Banach space with the norm
is a Banach space with the norm  . Let
. Let

Lemma 2.2.
Let  and
and  be as in Lemma 2.1, then
be as in Lemma 2.1, then

Proof.
Suppose  We have three different cases.
We have three different cases.
-
(i)
 . It follows from the concavity of
. It follows from the concavity of  that each point on the chard between
that each point on the chard between  and
and  is below the graph of
is below the graph of 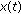 , thus
, thus  (2.7)
(2.7)then
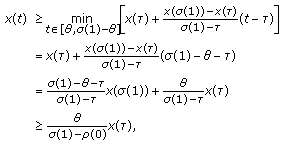 (2.8)
(2.8)this means
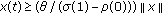 for
for 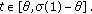
-
(ii)
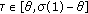 . If
. If  , similarly, we have
, similarly, we have  (2.9)
(2.9)If
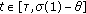 , similarly, we have
, similarly, we have (2.10)
(2.10)this means
 for
for  .
. -
(iii)
 . Similarly we have
. Similarly we have  (2.11)
(2.11)then
 (2.12)
(2.12)this means
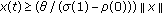 for
for 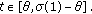 From the above, we know
From the above, we know (2.13)
(2.13)
Lemma 2.3.
Suppose that condition (H3) holds. Let  and
and  . Then
. Then  -Laplacian BVP (2.1)-(1.2) has a solution
-Laplacian BVP (2.1)-(1.2) has a solution

where  is a solution of the following equation
is a solution of the following equation

where

Proof.
Obviously  and
and  , beside these
, beside these  and
and  . So, there must be an intersection point between
. So, there must be an intersection point between  and
and  for
for  and
and  , which is a solution
, which is a solution  , since
, since  and
and  are continuous. It is easy to verify that
are continuous. It is easy to verify that  is a solution of (2.1)-(1.2). If (2.1) has a solution, denoted by
is a solution of (2.1)-(1.2). If (2.1) has a solution, denoted by  , then
, then  . There exists a constant
. There exists a constant  such that
such that  . If it does not hold, without loss of generality, one supposes that
. If it does not hold, without loss of generality, one supposes that  for
for  . From the boundary conditions, we have
. From the boundary conditions, we have

which is a contradiction.
Integrating (2.1) on  we get
we get

Then, we have

Using the second boundary condition and the formula (2.18) for  , we have
, we have

Also, using the formula (2.18), we have

Similarly, integrating (2.1) on  we get
we get

Throughout this paper, we assume that  .
.
Lemma 2.4.
Suppose that the conditions in Lemma 2.3 hold. Then there exists a constant  such that the solution
such that the solution  of
of  -Laplacian BVP (2.1)-(1.2) satisfies
-Laplacian BVP (2.1)-(1.2) satisfies

Proof.
It is clear that  satisfies
satisfies

Similarly,

If we define  , we get
, we get

Now, we define a mapping  given by
given by

Because of

we get  , for
, for  and
and  , for
, for  , thus the operator
, thus the operator  is monotone increasing on
is monotone increasing on  and monotone decreasing on
and monotone decreasing on  and also
and also  is the maximum point of the operator
is the maximum point of the operator  . So the operator
. So the operator  is concave on
is concave on  and
and  . Therefore,
. Therefore,  .
.
Lemma 2.5.
Suppose that the conditions (H1)–(H3) hold.  is completely continuous.
is completely continuous.
Proof.
Suppose  is a bounded set. Let
is a bounded set. Let  be such that
be such that  ,
,  . For any
. For any  , we have
, we have

Then,  is bounded.
is bounded.
By the Arzela-Ascoli theorem, we can easily see that  is completely continuous operator.
is completely continuous operator.
For convenience, we set

In order to follow the main results of this paper easily, now we state the fixed point theorems which we applied to prove Theorems 3.1–3.4.
Theorem 2.6 (see [18] (Krasnoselskii fixed point theorem)).
Let  be a Banach space, and let
be a Banach space, and let  be a cone. Assume
be a cone. Assume  and
and  are open, bounded subsets of
are open, bounded subsets of  with
with  , and let
, and let

be a completely continuous operator such that either
-
(i)
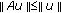 for
for 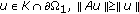 for
for 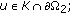
-
(ii)
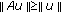 for
for  for
for 
hold. Then  has a fixed point in
has a fixed point in  .
.
Theorem 2.7 (see [19] (Schauder fixed point theorem)).
Let  be a Banach space, and let
be a Banach space, and let  be a completely continuous operator. Assume
be a completely continuous operator. Assume  is a bounded, closed, and convex set. If
is a bounded, closed, and convex set. If  , then
, then  has a fixed point in
has a fixed point in  .
.
Theorem 2.8 (see [20] (Avery-Henderson fixed point theorem)).
Let  be a cone in a real Banach space
be a cone in a real Banach space  . Set
. Set

If  and
and  are increasing, nonnegative, continuous functionals on
are increasing, nonnegative, continuous functionals on  , let
, let  be a nonnegative continuous functional on
be a nonnegative continuous functional on  with
with  such that for some positive constants
such that for some positive constants  and
and  ,
,

for all  . Suppose that there exist positive numbers
. Suppose that there exist positive numbers  such that
such that  for all
for all  and
and 
If  is a completely continuous operator satisfying
is a completely continuous operator satisfying
-
(i)
 for all
for all 
-
(ii)
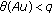 for all
for all 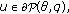
-
(iii)
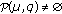 and
and 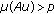 for all
for all  ,
,
then  has at least two fixed points
has at least two fixed points  and
and  such that
such that

3. Main Results
In this section, we will prove the existence of at least one and two positive solution of  -Laplacian BVP (1.1)-(1.2). In the following theorems we will make use of Krasnoselskii, Schauder, and Avery-Henderson fixed point theorems, respectively.
-Laplacian BVP (1.1)-(1.2). In the following theorems we will make use of Krasnoselskii, Schauder, and Avery-Henderson fixed point theorems, respectively.
Theorem 3.1.
Assume that (H1)–(H3) are satisfied. In addition, suppose that  satisfies
satisfies
-
(A1)
 for
for 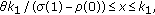
-
(A2)
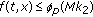 for
for 
where  and
and  . Then the
. Then the  -Laplacian BVP (1.1)-(1.2) has a positive solution
-Laplacian BVP (1.1)-(1.2) has a positive solution  such that
such that  .
.
Proof.
Without loss of generality, we suppose  . For any
. For any  , by Lemma 2.2, we have
, by Lemma 2.2, we have

We define two open subsets  and
and  of
of  such that
such that  and
and  .
.
For  , by (3.1), we have
, by (3.1), we have

For  , if
, if  holds, we will discuss it from three perspectives.
holds, we will discuss it from three perspectives.
-
(i)
If
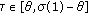 , thus for
, thus for 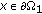 , by
, by  and Lemma 2.1, we have
and Lemma 2.1, we have  (3.3)
(3.3)
-
(ii)
If
 , thus for
, thus for 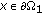 , by
, by  and Lemma 2.1, we have
and Lemma 2.1, we have  (3.4)
(3.4)
-
(iii)
If
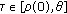 , thus for
, thus for  , by
, by  and Lemma 2.1, we have
and Lemma 2.1, we have  (3.5)
(3.5)
Therefore, we have  ,
,
On the other hand, as  , we have
, we have  , by
, by  , we know
, we know

Then,  has a fixed point
has a fixed point  . Obviously,
. Obviously,  is a positive solution of the
is a positive solution of the  -Laplacian BVP (1.1)-(1.2) and
-Laplacian BVP (1.1)-(1.2) and  .
.
Existence of at least one positive solution is also proved using Schauder fixed point theorem (Theorem 2.7). Then we have the following result.
Theorem 3.2.
Assume that (H1)–(H3) are satisfied. If  satisfies
satisfies

where  satisfies
satisfies

then the  -Laplacian BVP (1.1)-(1.2) has at least one positive solution.
-Laplacian BVP (1.1)-(1.2) has at least one positive solution.
Proof.
Let  . Note that
. Note that  is closed, bounded, and convex subset of
is closed, bounded, and convex subset of  to which the Schauder fixed point theorem is applicable. Define
to which the Schauder fixed point theorem is applicable. Define  as in (2.27) for
as in (2.27) for  . It can be shown that
. It can be shown that  is continuous. Claim that
is continuous. Claim that  . Let
. Let  . By using the similar methods used in the proof of Theorem 3.1, we have
. By using the similar methods used in the proof of Theorem 3.1, we have

which implies  . The compactness of the operator
. The compactness of the operator  follows from the Arzela-Ascoli theorem. Hence
follows from the Arzela-Ascoli theorem. Hence  has a fixed point in
has a fixed point in  .
.
Corollary 3.3.
If  is continuous and bounded on
is continuous and bounded on  , then the
, then the  -Laplacian BVP (1.1)-(1.2) has a positive solution.
-Laplacian BVP (1.1)-(1.2) has a positive solution.
Now we will give the sufficient conditions to have at least two positive solutions for  -Laplacian BVP (1.1)-(1.2). Set
-Laplacian BVP (1.1)-(1.2). Set

The function  is positive and continuous on
is positive and continuous on  . Therefore,
. Therefore,  has a minimum on
has a minimum on  . Hence we suppose there exists
. Hence we suppose there exists  such that
such that 
Also, we define the nonnegative, increasing continuous functions  and
and  by
by

We observe here that, for every  ,
,  and from Lemma 2.2,
and from Lemma 2.2,  . Also, for
. Also, for  ,
, 
Theorem 3.4.
Assume that (H1)–(H3) are satisfied. Suppose that there exist positive numbers  such that the function f satisfies the following conditions:
such that the function f satisfies the following conditions:
-
(i)
 for
for  ,
, -
(ii)
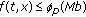 for
for  ,
, -
(iii)
 for
for 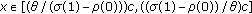 ,
,
for positive constants  ,
,  and
and  . Then the
. Then the  -Laplacian BVP (1.1)-(1.2) has at least two positive solutions
-Laplacian BVP (1.1)-(1.2) has at least two positive solutions  such that
such that

Proof.
Define the cone as in (2.5). From Lemmas 2.2 and 2.3 and the conditions (H1) and (H2), we can obtain  . Also from Lemma 2.5, we see that
. Also from Lemma 2.5, we see that  is completely continuous.
is completely continuous.
We now show that the conditions of Theorem 2.8 are satisfied.
To fulfill property (i) of Theorem 2.8, we choose  , thus
, thus  . Recalling that
. Recalling that  , we have
, we have

Then assumption (iii) implies  for
for  . We have three different cases.
. We have three different cases.
-
(a)
If
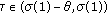 , we have
, we have  (3.14)
(3.14)
Thus we have  .
.
-
(b)
If
 , we have
, we have  (3.15)
(3.15)
Thus we have  .
.
-
(c)
If
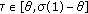 , we have
, we have 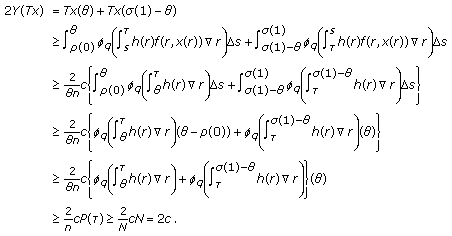 (3.16)
(3.16)
Thus we have  and condition (i) of Theorem 2.8 holds. Next we will show condition (ii) of Theorem 2.8 is satisfied. If
and condition (i) of Theorem 2.8 holds. Next we will show condition (ii) of Theorem 2.8 is satisfied. If  , then
, then  .
.
Noting that

we have  , for
, for  .
.
Then (ii) yields  for
for  .
.
As  so
so

So condition (ii) of Theorem 2.8 holds.
To fulfill property (iii) of Theorem 2.8, we note  ,
,  is a member of
is a member of  and
and  , so
, so  . Now choose
. Now choose  , then
, then  and this implies that
and this implies that  for
for  . It follows from the assumption (i), we have
. It follows from the assumption (i), we have  for
for  . As before we obtain the following cases.
. As before we obtain the following cases.
-
(a)
If
 , we have
, we have 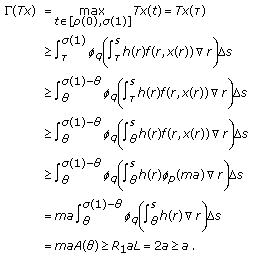 (3.19)
(3.19)
Thus we have  .
.
-
(b)
If
 , we have
, we have 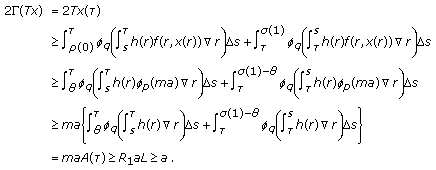 (3.20)
(3.20)
Thus we have  .
.
-
(c)
If
 , we have
, we have 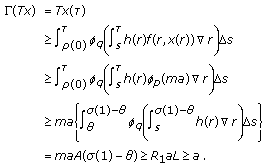 (3.21)
(3.21)
Thus we have  .
.
Therefore, condition (iii) of Theorem 2.8 holds. Since all conditions of Theorem 2.8 are satisfied, the  -Laplacian BVP (1.1)-(1.2) has at least two positive solutions
-Laplacian BVP (1.1)-(1.2) has at least two positive solutions  such that
such that

4. Monotone Method
In this section, we will prove the existence of solution of  -Laplacian BVP (1.1)-(1.2) by using upper and lower solution method. We define the set
-Laplacian BVP (1.1)-(1.2) by using upper and lower solution method. We define the set

Definition 4.1.
A real-valued function  on
on  is a lower solution for (1.1)-(1.2) if
is a lower solution for (1.1)-(1.2) if

Similarly, a real-valued function  on
on  is an upper solution for (1.1)-(1.2) if
is an upper solution for (1.1)-(1.2) if

We will prove when the lower and the upper solutions are given in the well order, that is,  , the
, the  -Laplacian BVP (1.1)-(1.2) admits a solution lying between both functions.
-Laplacian BVP (1.1)-(1.2) admits a solution lying between both functions.
Theorem 4.2.
Assume that (H1)–(H3) are satisfied and  and
and  are, respectively, lower and upper solutions for the
are, respectively, lower and upper solutions for the  -Laplacian BVP (1.1)-(1.2) such that
-Laplacian BVP (1.1)-(1.2) such that  on
on  . Then the
. Then the  -Laplacian BVP (1.1)-(1.2) has a solution
-Laplacian BVP (1.1)-(1.2) has a solution  on
on  .
.
Proof.
Consider the  -Laplacian BVP:
-Laplacian BVP:

where

for 
Clearly, the function  is bounded for
is bounded for  and satisfies condition (H1). Thus by Theorem 3.2, there exists a solution
and satisfies condition (H1). Thus by Theorem 3.2, there exists a solution  of the
of the  -Laplacian BVP (4.4). We first show that
-Laplacian BVP (4.4). We first show that  on
on  . Set
. Set  . If
. If  on
on  is not true, then there exists a
is not true, then there exists a  such that
such that  has a positive maximum. Consequently, we know that
has a positive maximum. Consequently, we know that  and there exists
and there exists  such that
such that  on
on  . On the other hand by the continuity of
. On the other hand by the continuity of  at
at  we know there exists
we know there exists  such that
such that  on
on  Let
Let  , then we have
, then we have  on
on  . Thus we get
. Thus we get

Therefore,

which is a contradiction and thus  cannot be an element of
cannot be an element of  .
.
If  , from the boundary conditions, we have
, from the boundary conditions, we have

Thus we get

From this inequalities, we have

which is a contradiction.
If  , from the boundary conditions, we have
, from the boundary conditions, we have

Thus we get

From this inequalities, we have

which is a contradiction. Thus we have  on
on  .
.
Similarly, we can get  on
on  . Thus
. Thus  is a solution of
is a solution of  -Laplacian BVP (1.1)-(1.2) which lies between
-Laplacian BVP (1.1)-(1.2) which lies between  and
and  .
.
References
Bohner M, Peterson A: Dynamic Equations on Time Scales, An Introduction with Application. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Bandle C, Kwong MK: Semilinear elliptic problems in annular domains. Journal of Applied Mathematics and Physics 1989,40(2):245-257. 10.1007/BF00945001
Wang H: On the existence of positive solutions for semilinear elliptic equations in the annulus. Journal of Differential Equations 1994,109(1):1-7. 10.1006/jdeq.1994.1042
Chyan CJ, Henderson J: Twin solutions of boundary value problems for differential equations on measure chains. Journal of Computational and Applied Mathematics 2002,141(1-2):123-131. 10.1016/S0377-0427(01)00440-X
Gatica JA, Oliker V, Waltman P: Singular nonlinear boundary value problems for second-order ordinary differential equations. Journal of Differential Equations 1989,79(1):62-78. 10.1016/0022-0396(89)90113-7
Avery R, Henderson J:Existence of three positive pseudo-symmetric solutions for a one dimensional
 -Laplacian. Journal of Mathematical Analysis and Applications 2001, 42: 593-601.
-Laplacian. Journal of Mathematical Analysis and Applications 2001, 42: 593-601.Cabada A:Extremal solutions for the difference
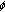 -Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001,42(3-5):593-601. 10.1016/S0898-1221(01)00179-1
-Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001,42(3-5):593-601. 10.1016/S0898-1221(01)00179-1He XM:The existence of positive solutions of
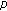 -Laplacian equation. Acta Mathematica Sinica 2003,46(4):805-810.
-Laplacian equation. Acta Mathematica Sinica 2003,46(4):805-810.Anderson DR: Solutions to second-order three-point problems on time scales. Journal of Difference Equations and Applications 2002,8(8):673-688. 10.1080/1023619021000000717
Atici FM, Guseinov GSh: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002,141(1-2):75-99. 10.1016/S0377-0427(01)00437-X
Akin E: Boundary value problems for a differential equation on a measure chain. Panamerican Mathematical Journal 2000,10(3):17-30.
Kaufmann ER: Positive solutions of a three-point boundary-value problem on a time scale. Electronic Journal of Differential Equations 2003, (82):1-11.
Agarwal RP, O'Regan D: Triple solutions to boundary value problems on time scales. Applied Mathematics Letters 2000,13(4):7-11. 10.1016/S0893-9659(99)00200-1
Song C, Weng P:Multiple positive solutions for
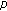 -Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043
-Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043Sun H-R, Li W-T:Existence theory for positive solutions to one-dimensional
 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004Liu B:Positive solutions of three-point boundary value problems for the one-dimensional
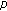 -Laplacian with infinitely many singularities. Applied Mathematics Letters 2004,17(6):655-661. 10.1016/S0893-9659(04)90100-0
-Laplacian with infinitely many singularities. Applied Mathematics Letters 2004,17(6):655-661. 10.1016/S0893-9659(04)90100-0Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Krasnosel'skii MA: Positive Solutions of Operator Equations. P. Noordhoff, Groningen, The Netherlands; 1964:381.
Avery RI, Henderson J: Two positive fixed points of nonlinear operators on ordered Banach spaces. Communications on Applied Nonlinear Analysis 2001,8(1):27-36.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Topal, S.G., Ozen, O.B. & Cetin, E. Existence of Solutions for Nonlinear Four-Point  -Laplacian Boundary Value Problems on Time Scales.
Adv Differ Equ 2009, 123565 (2009). https://doi.org/10.1155/2009/123565
-Laplacian Boundary Value Problems on Time Scales.
Adv Differ Equ 2009, 123565 (2009). https://doi.org/10.1155/2009/123565
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/123565
 ,
,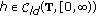 and does not vanish identically on any closed subinterval of
and does not vanish identically on any closed subinterval of 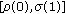 and
and  ,
,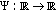 is continuous and satisfies that there exist
is continuous and satisfies that there exist 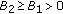 such that
such that 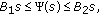 for
for 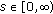 .
. . It follows from the concavity of
. It follows from the concavity of  that each point on the chard between
that each point on the chard between  and
and  is below the graph of
is below the graph of 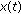 , thus
, thus 
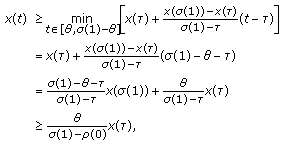
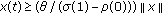 for
for 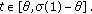
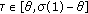 . If
. If  , similarly, we have
, similarly, we have 
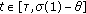 , similarly, we have
, similarly, we have
 for
for  .
. . Similarly we have
. Similarly we have 

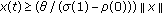 for
for 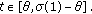 From the above, we know
From the above, we know
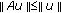 for
for 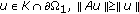 for
for 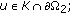
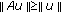 for
for  for
for 
 for all
for all 
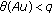 for all
for all 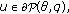
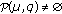 and
and 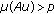 for all
for all  ,
, for
for 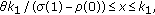
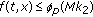 for
for 
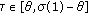 , thus for
, thus for 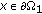 , by
, by  and Lemma 2.1, we have
and Lemma 2.1, we have 
 , thus for
, thus for 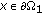 , by
, by  and Lemma 2.1, we have
and Lemma 2.1, we have 
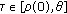 , thus for
, thus for  , by
, by  and Lemma 2.1, we have
and Lemma 2.1, we have 
 for
for  ,
,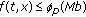 for
for  ,
, for
for 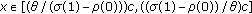 ,
,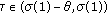 , we have
, we have 
 , we have
, we have 
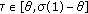 , we have
, we have 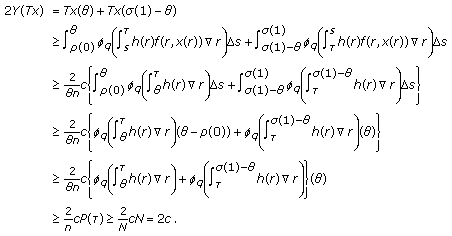
 , we have
, we have 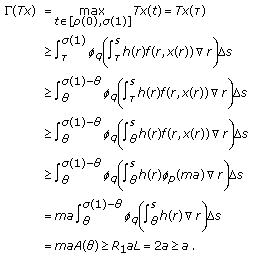
 , we have
, we have 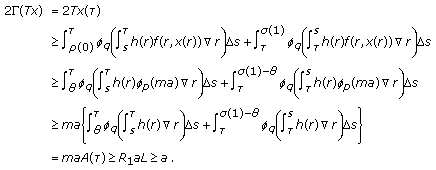
 , we have
, we have 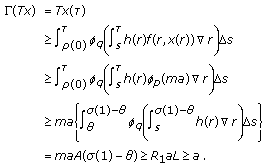
 -Laplacian. Journal of Mathematical Analysis and Applications 2001, 42: 593-601.
-Laplacian. Journal of Mathematical Analysis and Applications 2001, 42: 593-601.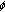 -Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001,42(3-5):593-601. 10.1016/S0898-1221(01)00179-1
-Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001,42(3-5):593-601. 10.1016/S0898-1221(01)00179-1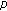 -Laplacian equation. Acta Mathematica Sinica 2003,46(4):805-810.
-Laplacian equation. Acta Mathematica Sinica 2003,46(4):805-810.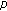 -Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043
-Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004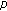 -Laplacian with infinitely many singularities. Applied Mathematics Letters 2004,17(6):655-661. 10.1016/S0893-9659(04)90100-0
-Laplacian with infinitely many singularities. Applied Mathematics Letters 2004,17(6):655-661. 10.1016/S0893-9659(04)90100-0