- Research Article
- Open access
- Published:
Reducibility and Stability Results for Linear System of Difference Equations
Advances in Difference Equations volume 2008, Article number: 867635 (2008)
Abstract
We first give a theorem on the reducibility of linear system of difference equations of the form  . Next, by the means of Floquet theory, we obtain some stability results. Moreover, some examples are given to illustrate the importance of the results.
. Next, by the means of Floquet theory, we obtain some stability results. Moreover, some examples are given to illustrate the importance of the results.
1. Introduction
Consider the homogeneous linear system of difference equations

where  is a
is a  nonsingular matrix with real entries and
nonsingular matrix with real entries and 
If for some 

is specified, then (1.1) is called an initial value problem (IVP). The solution of this IVP is given by

where  is the fundamental matrix defined by
is the fundamental matrix defined by

However, (1.1) is called reducible to equation

if there is a nonsingular matrix  with real entries such that
with real entries such that

Let  be a
be a  matrix function whose entries are real-valued functions defined for
matrix function whose entries are real-valued functions defined for  . Consider the system
. Consider the system

Let  be a fundamental matrix of (1.7) satisfying
be a fundamental matrix of (1.7) satisfying  . This
. This  can be used to transform (1.1) into (1.5).
can be used to transform (1.1) into (1.5).
Stability properties of (1.1) can be deduced by considering the reduced form (1.5) under some additional conditions. In this study, we first give a theorem on the reducibility of (1.1) into the form of (1.5) and then obtain asymptotic stability of the zero solution of (1.1).
2. Reducible Systems
In this section, we give a theorem on the structure of the matrix  , and provide an example for illustration. The results in this section are discrete analogues of the ones given in [1].
, and provide an example for illustration. The results in this section are discrete analogues of the ones given in [1].
Theorem 2.1.
The homogeneous linear difference system (1.1) is reducible to (1.5) under the transformation (1.6) if and only if there exists a  regular real matrix
regular real matrix  such that
such that

hold.
Proof.
Let  and
and  be defined as above. Under the transformation (1.6), (1.1) becomes
be defined as above. Under the transformation (1.6), (1.1) becomes

and after reorganizing, we get

Thus, (1.1) is reducible to (1.5) with

Clearly,  is the unique solution of the IVP:
is the unique solution of the IVP:

where 
This problem is equivalent to solving (2.1). □
Corollary 2.2.
The homogeneous linear system of difference equation (1.1) is reducible to

with a constant matrix  under transformation (1.6) if and only if there exists a
under transformation (1.6) if and only if there exists a  regular real matrix
regular real matrix  defined for
defined for  such that
such that


hold.
Below, we give an example for Corollary 2.2 in the special case  . To obtain the matrix
. To obtain the matrix  , we choose a suitable form of the matrix
, we choose a suitable form of the matrix  .
.
Example 2.3.
Consider the system

where
-
(i)
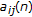 are real-valued functions defined for
are real-valued functions defined for 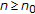 such that
such that  for all
for all 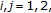
-
(ii)
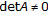 for all
for all 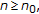
-
(iii)
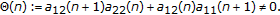
We also assume that for all  ,
,

It is easy to verify that if we take

where



then (2.7) holds. Moreover, from (2.8) we have

In case  for every
for every  , that is,
, that is,

the relations (2.10), (2.12), and (2.13) take the form

where  is a real constant and
is a real constant and  ,
,  are arbitrary real constants such that
are arbitrary real constants such that 
Corollary 2.4.
If there exists a  regular constant matrix
regular constant matrix  such that
such that

then (1.1) reduces to (2.6) with 
It should be noted that in case the constant matrices  and
and  commute, that is,
commute, that is,  , then
, then  must be a constant matrix as well.
must be a constant matrix as well.
3. Stability of Linear Systems
It turns out that to obtain a stability result, one needs take  , a periodic matrix [2]. Indeed, this allows using the Floquet theory for linear periodic system (1.7).
, a periodic matrix [2]. Indeed, this allows using the Floquet theory for linear periodic system (1.7).
We need the following three well-known theorems [3–5].
Theorem 3.1.
Let  be the fundamental matrix of (1.1) with
be the fundamental matrix of (1.1) with 
The zero solution of (1.1) is
-
(i)
stable if and only if there exists a positive constant M such that
 (3.1)
(3.1) -
(ii)
asymptotically stable if and only if
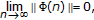 (3.2)
(3.2)where
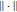 is a norm in
is a norm in .
.
Theorem 3.2.
Consider system (1.1) with  a constant regular matrix. Then its zero solution is
a constant regular matrix. Then its zero solution is
-
(i)
stable if and only if
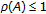 and the eigenvalues of unit modulus are semisimple;
and the eigenvalues of unit modulus are semisimple; -
(ii)
asymptotically stable if and only if
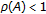 , where
, where 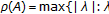 is an eigenvalue of
is an eigenvalue of is the spectral radius of
is the spectral radius of 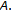
Consider the linear periodic system

where  ,
,  for some positive integer N.
for some positive integer N.
From the literature, we know that if  with
with  is a fundamental matrix of (3.3), then there exists a constant
is a fundamental matrix of (3.3), then there exists a constant  matrix, whose eigenvalues are called the Floquet exponents, and periodic matrix
matrix, whose eigenvalues are called the Floquet exponents, and periodic matrix  with period N such that
with period N such that 
Theorem 3.3.
The zero solution of (3.3) is
-
(i)
stable if and only if the Floquet exponents have modulus less than or equal to one; those with modulus of one are semisimple;
-
(ii)
asymptotically stable if and only if all the Floquet exponents lie inside the unit disk.
In view of Theorems 3.1, 3.2, and 3.3, we obtain from Corollary 2.2 the following new stability criteria for (1.1).
Theorem 3.4.
The zero solution of (1.1) is stable if and only if there exists a  regular periodic matrix
regular periodic matrix  satisfying (2.8) such that
satisfying (2.8) such that
-
(i)
the Floquet exponents of
 have modulus less than or equal to one; those with modulus of one are semisimple;
have modulus less than or equal to one; those with modulus of one are semisimple; -
(ii)
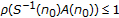 ; those eigenvalues of
; those eigenvalues of 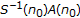 of unit modulus are semisimple.
of unit modulus are semisimple.
Theorem 3.5.
The zero solution of (1.1) is asymptotically stable if and only if there exists a  regular periodic matrix
regular periodic matrix  satisfying (2.8) such that either
satisfying (2.8) such that either
-
(i)
all the Floquet exponents of
 lie inside the unit disk and
lie inside the unit disk and 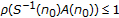 ; those eigenvalues of
; those eigenvalues of 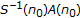 of unit modulus are semisimple; or
of unit modulus are semisimple; or -
(ii)
the Floquet exponents of
 have modulus less than or equal to one; those with modulus of one are semisimple; and
have modulus less than or equal to one; those with modulus of one are semisimple; and 
Remark 3.6.
Let  be periodic with period N. The Floquet exponents mentioned in Theorem 3.3 are the eigenvalues of
be periodic with period N. The Floquet exponents mentioned in Theorem 3.3 are the eigenvalues of  where
where 
Example 3.7.
Consider the system

Note that the conditions of Example 2.3 are all satisfied. It follows that

Now,

for which the eigenvalues are 
On the other hand, for

 if
if  and
and  if
if  .
.
Applying Theorems 3.4 and 3.5, we see that the zero solution of (3.4) is asymptotically stable if  and is stable if
and is stable if 
In fact, the unique solution of (3.4) satisfying  is
is

where  ,
,  ,
,  ,
,  , and
, and  .
.
It is easy to see that  if
if  and
and  is bounded if
is bounded if 
Remark 3.8.
In the computation of  ,
,  is calculated by using Example 2.3, and
is calculated by using Example 2.3, and  is obtained by the method given in [6, 7].
is obtained by the method given in [6, 7].
References
Tiryaki A:On the equation
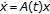 . Mathematica Japonica 1988, 33(3):469-473.
. Mathematica Japonica 1988, 33(3):469-473.Rodriguez J, Etheridge DL: Periodic solutions of nonlinear second-order difference equations. Advances in Difference Equations 2005, 2005(2):173-192. 10.1155/ADE.2005.173
Elaydi SN: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. Springer, New York, NY, USA; 1996:xiv+389.
Kipnis M, Komissarova D: Stability of a delay difference system. Advances in Difference Equations 2006, 2006:-9.
Lakshmikantham V, Trigiante D: Theory of Difference Equations: Numerical Methods and Application, Mathematics in Science and Engineering. Volume 181. Academic Press, Boston, Mass, USA; 1988:x+242.
Elaydi SN, Harris WA Jr.:On the computation of
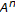 . SIAM Review 1998, 40(4):965-971. 10.1137/S0036144597319235
. SIAM Review 1998, 40(4):965-971. 10.1137/S0036144597319235Zafer A: Calculating the matrix exponential of a constant matrix on time scales. Applied Mathematics Letters 2008, 21(6):612-616. 10.1016/j.aml.2007.06.006
Acknowledgment
The authors would like to thank to Professor Ağacık Zafer for his valuable contributions to Section 3.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tiryaki, A., Misir, A. Reducibility and Stability Results for Linear System of Difference Equations. Adv Differ Equ 2008, 867635 (2008). https://doi.org/10.1155/2008/867635
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/867635
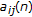 are real-valued functions defined for
are real-valued functions defined for 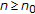 such that
such that  for all
for all 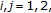
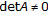 for all
for all 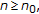
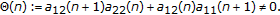

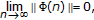
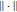 is a norm in
is a norm in .
.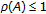 and the eigenvalues of unit modulus are semisimple;
and the eigenvalues of unit modulus are semisimple;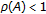 , where
, where 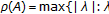 is an eigenvalue of
is an eigenvalue of is the spectral radius of
is the spectral radius of 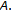
 have modulus less than or equal to one; those with modulus of one are semisimple;
have modulus less than or equal to one; those with modulus of one are semisimple;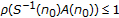 ; those eigenvalues of
; those eigenvalues of 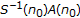 of unit modulus are semisimple.
of unit modulus are semisimple. lie inside the unit disk and
lie inside the unit disk and 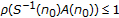 ; those eigenvalues of
; those eigenvalues of 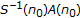 of unit modulus are semisimple; or
of unit modulus are semisimple; or have modulus less than or equal to one; those with modulus of one are semisimple; and
have modulus less than or equal to one; those with modulus of one are semisimple; and 
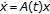 . Mathematica Japonica 1988, 33(3):469-473.
. Mathematica Japonica 1988, 33(3):469-473.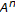 . SIAM Review 1998, 40(4):965-971. 10.1137/S0036144597319235
. SIAM Review 1998, 40(4):965-971. 10.1137/S0036144597319235