- Review Article
- Open access
- Published:
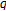 -Genocchi Numbers and Polynomials Associated with
-Genocchi Numbers and Polynomials Associated with 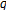 -Genocchi-Type
-Genocchi-Type  -Functions
-Functions
Advances in Difference Equations volume 2008, Article number: 815750 (2007)
Abstract
The main purpose of this paper is to study on generating functions of the 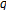 -Genocchi numbers and polynomials. We prove new relation for the generalized
-Genocchi numbers and polynomials. We prove new relation for the generalized 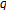 -Genocchi numbers which is related to the
-Genocchi numbers which is related to the 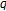 -Genocchi numbers and
-Genocchi numbers and 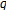 -Bernoulli numbers. By applying Mellin transformation and derivative operator to the generating functions, we define
-Bernoulli numbers. By applying Mellin transformation and derivative operator to the generating functions, we define 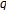 -Genocchi zeta and
-Genocchi zeta and  -functions, which are interpolated
-functions, which are interpolated 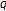 -Genocchi numbers and polynomials at negative integers. We also give some applications of generalized
-Genocchi numbers and polynomials at negative integers. We also give some applications of generalized 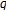 -Genocchi numbers.
-Genocchi numbers.
1. Introduction Definitions and Notations
In [1], Jang et al. gave new formulae on Genocchi numbers. They defined poly-Genocchi numbers to give the relation between Genocchi numbers, Euler numbers, and poly-Genocchi numbers. In [2], Kim et al. constructed new generating functions of the  -analogue Eulerian numbers and
-analogue Eulerian numbers and  -analogue Genocchi numbers. They gave relations between Bernoulli numbers, Euler numbers, and Genocchi numbers. They also defined Genocchi zeta functions which interpolate these numbers at negative integers. Kim [3] gave new concept of the
-analogue Genocchi numbers. They gave relations between Bernoulli numbers, Euler numbers, and Genocchi numbers. They also defined Genocchi zeta functions which interpolate these numbers at negative integers. Kim [3] gave new concept of the  -extension of Genocchi numbers and gave some relations between
-extension of Genocchi numbers and gave some relations between  -Genocchi polynomials and
-Genocchi polynomials and  -Euler numbers. In this paper, by using generating function of this numbers, we study on
-Euler numbers. In this paper, by using generating function of this numbers, we study on  -Genocchi zeta and
-Genocchi zeta and  -functions. In [4], Kim constructed
-functions. In [4], Kim constructed  -Genocchi numbers and polynomials. By using these numbers and polynomials, he proved the
-Genocchi numbers and polynomials. By using these numbers and polynomials, he proved the  -analogue of alternating sums of powers of consecutive integers due to Euler:
-analogue of alternating sums of powers of consecutive integers due to Euler:

(cf. [4]), where if 

and the numbers  are called
are called  -Genocchi numbers which are defined by
-Genocchi numbers which are defined by

Note that  (cf. [3, 5–9]). The Euler numbers
(cf. [3, 5–9]). The Euler numbers  are usually defined by means of the following generating function (cf. [10–16]):
are usually defined by means of the following generating function (cf. [10–16]):

The Genocchi numbers  are usually defined by means of the following generating function (cf. [12, 13]):
are usually defined by means of the following generating function (cf. [12, 13]):

These numbers are classical and important in number theory. In [12], Kim defined generating functions of the  -Genocchi numbers and
-Genocchi numbers and  -Euler numbers as follows:
-Euler numbers as follows:

where  denotes
denotes  -Euler numbers,
-Euler numbers,

where  denotes
denotes  -Genocchi numbers. Genocchi zeta function is defined as follows (cf. [13, page 108]): for
-Genocchi numbers. Genocchi zeta function is defined as follows (cf. [13, page 108]): for 

Kim [17] defined the ferminoic and deformic expression of  -adic
-adic  -Volkenborn integral at
-Volkenborn integral at  and
and  He constructed integral equation of the fermionic expression of
He constructed integral equation of the fermionic expression of  -adic
-adic  -Volkenborn integral at
-Volkenborn integral at  By using this integral equation, he defined new generating functions of
By using this integral equation, he defined new generating functions of  -Euler numbers and polynomials. By using derivative operator to this functions, he constructed new
-Euler numbers and polynomials. By using derivative operator to this functions, he constructed new  -zeta,
-zeta,  -
- -functions and
-functions and  -adic
-adic  -
- -functions, which are interpolated
-functions, which are interpolated  -Euler numbers and polynomials. He also gave some applications which are the formulae of the trigonometric functions by applying ferminoic and deformic expression of
-Euler numbers and polynomials. He also gave some applications which are the formulae of the trigonometric functions by applying ferminoic and deformic expression of  -adic
-adic  -Volkenborn integral at
-Volkenborn integral at  and
and  Kim and Rim [18] defined two-variable
Kim and Rim [18] defined two-variable  -function. They gave main properties of this function. In [6], Kim constructed the two-variable
-function. They gave main properties of this function. In [6], Kim constructed the two-variable  -adic
-adic  -
- -function which interpolates the generalized
-function which interpolates the generalized  -Bernoulli polynomials attached to Dirichlet character. In [19], Simsek et al. constructed the two-variable Dirichlet
-Bernoulli polynomials attached to Dirichlet character. In [19], Simsek et al. constructed the two-variable Dirichlet  -
- -function and the two-variable multiple Dirichlet-type Changhee
-function and the two-variable multiple Dirichlet-type Changhee  -
- -function. In [8, 20], Simsek defined generating functions, which are interpolates twisted Bernoulli numbers and polynomials, twisted Euler numbers and polynomials. He[21] also gave new generating functions which produce
-function. In [8, 20], Simsek defined generating functions, which are interpolates twisted Bernoulli numbers and polynomials, twisted Euler numbers and polynomials. He[21] also gave new generating functions which produce  -Genocchi zeta functions and
-Genocchi zeta functions and  -
- -series with attached to Dirichlet character. Therefore, by using these generating functions, he constructed new
-series with attached to Dirichlet character. Therefore, by using these generating functions, he constructed new  -analogue of Hardy-Berndt sums. He gave relations between these sums,
-analogue of Hardy-Berndt sums. He gave relations between these sums,  -Genocchi zeta functions and
-Genocchi zeta functions and  -
- -series as well,
-series as well,

(cf. [21]), where  is Euler's gamma function and
is Euler's gamma function and  (cf. [1], [13, page 108, equation (2.43)]). The first author defined
(cf. [1], [13, page 108, equation (2.43)]). The first author defined  -analogue of the Genocchi zeta functions as follows [21].
-analogue of the Genocchi zeta functions as follows [21].
Definition 1.1.
Let  and
and  .
.  -analogue of the Genocchi type zeta function is expressed by the formula
-analogue of the Genocchi type zeta function is expressed by the formula

Remark 1.2.
If  then (1.10) reduces to ordinary Genocchi zeta functions (see [13, page 108]). Cenkci et al. [22], defined different type of
then (1.10) reduces to ordinary Genocchi zeta functions (see [13, page 108]). Cenkci et al. [22], defined different type of  -Genocchi zeta functions, which are defined as follows:
-Genocchi zeta functions, which are defined as follows:

Simsek [21] defined  -analogue of the Hurwitz-type Genocchi zeta function by applying the Mellin transformations as follows:
-analogue of the Hurwitz-type Genocchi zeta function by applying the Mellin transformations as follows:

Definition 1.3 ({see [21]}).
Let  ,
,  and
and  .
.  -analogue of the Hurwitz-type Genocchi zeta function is expressed by the formula
-analogue of the Hurwitz-type Genocchi zeta function is expressed by the formula

Observe that when  the
the  is reduced to
is reduced to  and if
and if  then
then  A function
A function  is called an ordinary Hurwitz-type Genocchi zeta function if
is called an ordinary Hurwitz-type Genocchi zeta function if  is expressed by the formula
is expressed by the formula

where  ,
,  , and
, and  , cf. [13].
, cf. [13].
In [21], Simsek defined  -analogue (Genocchi-type) one- and two-variable
-analogue (Genocchi-type) one- and two-variable  -functions as follows, respectively; let
-functions as follows, respectively; let  be a Dirichlet character; let
be a Dirichlet character; let  and
and 


A function  is called an ordinary Genocchi-type
is called an ordinary Genocchi-type  -function if
-function if  is expressed by the formula
is expressed by the formula

where  and
and  cf. [13].
cf. [13].
Observe that when  (1.15) reduces to (1.10):
(1.15) reduces to (1.10):

We summarize our work as follows. In Section 2, we study on generating functions of the  -Genocchi numbers and polynomials. By using infinite and finite series, we give some definitions of the
-Genocchi numbers and polynomials. By using infinite and finite series, we give some definitions of the  -Genocchi numbers and polynomials. We find new relations between generalized
-Genocchi numbers and polynomials. We find new relations between generalized  -Genocchi numbers with attached to
-Genocchi numbers with attached to 
 -Genocchi numbers and Barnes' type Changhee
-Genocchi numbers and Barnes' type Changhee  -Bernoulli numbers. In Section 3, by applying Mellin transformation and derivative operator to the generating functions of the
-Bernoulli numbers. In Section 3, by applying Mellin transformation and derivative operator to the generating functions of the  -Genocchi numbers, we construct
-Genocchi numbers, we construct  -Genocchi zeta and
-Genocchi zeta and  -functions, which are interpolated
-functions, which are interpolated  -Genocchi numbers and polynomials at negative integers. We also give some new relations related to these numbers and polynomials.
-Genocchi numbers and polynomials at negative integers. We also give some new relations related to these numbers and polynomials.
2. 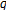 -genocchi Number and Polynomials
-genocchi Number and Polynomials
In this section, we give some new relations and identities related to  -Genocchi numbers and polynomials. Firstly we give some generating functions of the
-Genocchi numbers and polynomials. Firstly we give some generating functions of the  -Genocchi numbers, which were defined by Kim [3, 10, 11]:
-Genocchi numbers, which were defined by Kim [3, 10, 11]:

and let

(cf.[3, 10, 11, 23]), where  denotes
denotes  -Genocchi numbers.
-Genocchi numbers.
We note that  -Genocchi numbers,
-Genocchi numbers,  were defined by Kim [3, 10, 11].
were defined by Kim [3, 10, 11].
By using the above generating functions,  -Genocchi polynomials,
-Genocchi polynomials,  , are defined by means of the following generating function:
, are defined by means of the following generating function:

Our generating function of  is similar to that of [3, 12, 21, 23]. By using Cauchy product in (2.3), we easily obtain
is similar to that of [3, 12, 21, 23]. By using Cauchy product in (2.3), we easily obtain

Then by comparing coefficients of  on both sides of the above equation, for
on both sides of the above equation, for  we obtain the following result.
we obtain the following result.
Theorem 2.1.
Let  be an integer with
be an integer with  Then one has
Then one has

By using the same method in [3, 12, 21] in (2.3), we have

and after some elementary calculations, we have

By comparing coefficients of  on both sides of the above equation, we arrive at the following corollary.
on both sides of the above equation, we arrive at the following corollary.
Corollary 2.2.
Let  . Then one has
. Then one has

We give some of  -Genocchi polynomials as follows:
-Genocchi polynomials as follows: 

From the generating function  we have the following.
we have the following.
Corollary 2.3.
Let  . Then one has
. Then one has

Proof of the Corollary 2.3 was given by Kim [3, 12]. We give some of  -Genocchi numbers as follows:
-Genocchi numbers as follows:  ,
, 
Observe that if  then
then 
By using derivative operator to (2.6), we have

After some elementary calculations, we arrive at the following corollary.
Corollary 2.4.
Let  be a positive integer. Then one has
be a positive integer. Then one has

Corollary 2.5.
Let  be a positive integer. Then one has
be a positive integer. Then one has

Proof.
Proof of this corollary is easily obtained from (2.4).
Generalized  -Genocchi numbers are defined by means of the following generating function (this generating function is similar to that of [3, 12, 21–24]):
-Genocchi numbers are defined by means of the following generating function (this generating function is similar to that of [3, 12, 21–24]):

where  denotes the Dirichlet character with conductor
denotes the Dirichlet character with conductor  the set of positive integers.
the set of positive integers.
Observe that when  (2.13) reduces to (2.3).
(2.13) reduces to (2.3).
By (2.13), we have

After some elementary calculations and by comparing coefficients  on both sides of the above equation, we get
on both sides of the above equation, we get

By setting  , where
, where 
 and
and  , in the above equation, we obtain
, in the above equation, we obtain

In [15], Srivastava et al. defined the following generalized Barnes-type Changhee  -Bernoulli numbers.
-Bernoulli numbers.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . Then the generalized Barnes-type Changhee
. Then the generalized Barnes-type Changhee  -Bernoulli numbers with attached to
-Bernoulli numbers with attached to  are defined as follows:
are defined as follows:

(cf. [15]). Substituting  and
and  into the above equation, we have
into the above equation, we have

By using derivative operator to the above, we obtain

By substituting (2.9) and (2.19) into (2.16), after some calculations, we arrive at the following theorem.
Theorem 2.6.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . If
. If  is odd, then one has
is odd, then one has

if  is even, then one has
is even, then one has

where  is defined in (2.19).
is defined in (2.19).
Remark 2.7.
In Theorem 2.6, we give new relations between generalized  -Genocchi numbers,
-Genocchi numbers,  with attached to
with attached to  ,
,  -Genocchi numbers,
-Genocchi numbers,  , and Barnes-type Changhee
, and Barnes-type Changhee  -Bernoulli numbers. For detailed information about generalized Barnes-type Changhee
-Bernoulli numbers. For detailed information about generalized Barnes-type Changhee  -Bernoulli numbers with attached to
-Bernoulli numbers with attached to  see [15].
see [15].
Generalized Genocchi polynomials are defined by means of the following generating function:

Theorem 2.8.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . Then one has
. Then one has

Remark 2.9.
Generating functions of  and
and  are different from those of [3, 12, 22, 23]. Kim defined generating function of
are different from those of [3, 12, 22, 23]. Kim defined generating function of  as follows [12]:
as follows [12]:

In [21], Simsek defined generating function of  by
by

3. 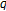 -genocchi Zeta and
-genocchi Zeta and  -Functions
-Functions
In recent years, many mathematicians and physicians have investigated zeta functions, multiple zeta functions,  -series,
-series,  -Genocchi zeta, and
-Genocchi zeta, and  -functions, and
-functions, and  -Bernoulli, Euler, and Genocchi numbers and polynomials mainly because of their interest and importance. These functions and numbers are not only used in complex analysis, but also used in
-Bernoulli, Euler, and Genocchi numbers and polynomials mainly because of their interest and importance. These functions and numbers are not only used in complex analysis, but also used in  -adic analysis and other areas. In particular, multiple zeta functions occur within the context of Knot theory, quantum field theory, applied analysis and number theory, (cf. [15]). In this section, we define
-adic analysis and other areas. In particular, multiple zeta functions occur within the context of Knot theory, quantum field theory, applied analysis and number theory, (cf. [15]). In this section, we define  -Genocchi zeta and
-Genocchi zeta and  -functions, which are interpolated
-functions, which are interpolated  -Genocchi polynomials and generalized
-Genocchi polynomials and generalized  -Genocchi numbers at negative integers. By applying the Mellin transformation to (2.3), we obtain
-Genocchi numbers at negative integers. By applying the Mellin transformation to (2.3), we obtain

where  ,
,  and
and  .
.
Thus, Hurwitz-type  -Genocchi zeta function is defined by the following definition.
-Genocchi zeta function is defined by the following definition.
Definition 3.1.
Let  with
with  and let
and let  with
with  Thenone defines
Thenone defines

Observe that when  in (3.2), then we obtain Riemann-type
in (3.2), then we obtain Riemann-type  -Genocchi zeta function:
-Genocchi zeta function:

Hurwitz-type  -Genocchi zeta function interpolates
-Genocchi zeta function interpolates  -Genocchi polynomials at negative integers. For
-Genocchi polynomials at negative integers. For  ,
,  , and by applying Cauchy residue theorem to (3.1), we can obtain the following theorem.
, and by applying Cauchy residue theorem to (3.1), we can obtain the following theorem.
Theorem 3.2.
For  ,
,  then one has
then one has

Remark 3.3.
The second proof of Theorem 3.2 can be obtained by using  derivative operator to (2.3) as follows:
derivative operator to (2.3) as follows:

Thus we obtained the desired result.
By applying Mellin transformation to (2.13), we obtain

Thus we can define Dirichlet-type  -Genocchi
-Genocchi  -function as follows.
-function as follows.
Definition 3.4.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . Let
. Let  with
with  One defines
One defines

Relation between  and
and  is given by the following theorem.
is given by the following theorem.
Theorem 3.5.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . Then one has
. Then one has

Proof.
By setting  where
where 
 in (3.7), we obtain,
in (3.7), we obtain,

After some elementary calculations, we arrive at the desired result of the theorem.
The function  interpolates generalized
interpolates generalized  -Genocchi numbers, which are given by the following theorem.
-Genocchi numbers, which are given by the following theorem.
Theorem 3.6.
Let  Let
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  Then one has
Then one has

Proof.
Proof of this theorem is similar to that of Theorem 3.2. So we omit the proof.
We give some applications. Setting 
 and using Theorem 3.2 in Theorem 3.5, we get
and using Theorem 3.2 in Theorem 3.5, we get

By comparing both sides of the above equation and Theorem 3.6, we obtain distributions relation of the generalized Genocchi numbers as follows.
Corollary 3.7.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  Then one has
Then one has

where  and
and  is the
is the  -Genocchi polynomial.
-Genocchi polynomial.
By substituting (2.5) into (3.12), we have the following corollary.
Corollary 3.8.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . Then one has
. Then one has

If we substitute (2.7) into (3.12), we get a new relation for the distribution relation of  -Genocchi numbers:
-Genocchi numbers:

Thus we arrive at the following corollary.
Corollary 3.9.
Let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  . Then one has
. Then one has

References
Jang L-C, Kim T, Lee D-H, Park D-W: An application of polylogarithms in the analogs of Genocchi numbers. Notes on Number Theory and Discrete Mathematics 2001, 7(3):65-69.
Kim T, Jang L-C, Pak HK:A note on
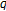 -Euler and Genocchi numbers. Proceedings of the Japan Academy. Series A 2001, 77(8):139-141. 10.3792/pjaa.77.139
-Euler and Genocchi numbers. Proceedings of the Japan Academy. Series A 2001, 77(8):139-141. 10.3792/pjaa.77.139Kim T:A note on the
 -Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8.
-Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8.Rim S-H, Kim T, Ryoo CS:On the alternating sums of powers of consecutive
 -integers. Bulletin of the Korean Mathematical Society 2006, 43(3):611-617.
-integers. Bulletin of the Korean Mathematical Society 2006, 43(3):611-617.Kim T:Sums of powers of consecutive
 -integers. Advanced Studies in Contemporary Mathematics 2004, 9(1):15-18.
-integers. Advanced Studies in Contemporary Mathematics 2004, 9(1):15-18.Kim T:Power series and asymptotic series associated with the
 -analog of the two-variable
-analog of the two-variable  -adic
-adic  -function. Russian Journal of Mathematical Physics 2005, 12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005, 12(2):186-196.Kim T, Rim S-H, Simsek Y:A note on the alternating sums of powers of consecutive
 -integers. Advanced Studies in Contemporary Mathematics 2006, 13(2):159-164.
-integers. Advanced Studies in Contemporary Mathematics 2006, 13(2):159-164.Simsek Y:
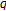 -analogue of twisted
-analogue of twisted  -series and
-series and 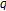 -twisted Euler numbers. Journal of Number Theory 2005, 110(2):267-278. 10.1016/j.jnt.2004.07.003
-twisted Euler numbers. Journal of Number Theory 2005, 110(2):267-278. 10.1016/j.jnt.2004.07.003Simsek Y, Kim D, Kim T, Rim S-H:A note on the sums of powers of consecutive
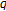 -integers. Journal of Applicable Functional Differential Equations 2006, 1(1):81-88.
-integers. Journal of Applicable Functional Differential Equations 2006, 1(1):81-88.Kim T:A note on
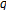 -Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005, 8(1):13-17.
-Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005, 8(1):13-17.Kim T:
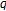 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic 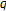 -integrals. Journal of Nonlinear Mathematical Physics 2007, 14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007, 14(1):15-27. 10.2991/jnmp.2007.14.1.3Kim T:On the
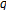 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007, 326(2):1458-1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007, 326(2):1458-1465. 10.1016/j.jmaa.2006.03.037Kim T, et al.: Introduction to Non-Archimedian Analysis, Kyo Woo Sa. Korea, 2004, http://www.kyowoo.co.kr/
Shiratani K, Yamamoto S:On a
 -adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985, 39(1):113-125. 10.2206/kyushumfs.39.113
-adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985, 39(1):113-125. 10.2206/kyushumfs.39.113Srivastava HM, Kim T, Simsek Y:
 -Bernoulli numbers and polynomials associated with multiple
-Bernoulli numbers and polynomials associated with multiple 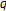 -zeta functions and basic
-zeta functions and basic 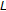 -series. Russian Journal of Mathematical Physics 2005, 12(2):241-268.
-series. Russian Journal of Mathematical Physics 2005, 12(2):241-268.Waldschmidt M, Moussa P, Luck JM, Itzykson C (Eds): From Number Theory to Physics. Springer, Berlin, Germany; 1995.
Kim T:On the analogs of Euler numbers and polynomials associated with
 -adic
-adic 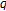 -integral on
-integral on 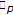 at
at 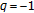 . Journal of Mathematical Analysis and Applications 2007, 331(2):779-792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007, 331(2):779-792. 10.1016/j.jmaa.2006.09.027Kim T, Rim S-H:A note on two variable Dirichlet's
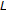 -function. Advanced Studies in Contemporary Mathematics 2005, 10(1):1-6.
-function. Advanced Studies in Contemporary Mathematics 2005, 10(1):1-6.Simsek Y, Kim D, Rim S-H:On the two-variable Dirichlet
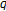 -
-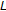 -series. Advanced Studies in Contemporary Mathematics 2005, 10(2):131-142.
-series. Advanced Studies in Contemporary Mathematics 2005, 10(2):131-142.Simsek Y:
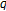 -Dedekind type sums related to
-Dedekind type sums related to 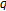 -zeta function and basic
-zeta function and basic  -series. Journal of Mathematical Analysis and Applications 2006, 318(1):333-351. 10.1016/j.jmaa.2005.06.007
-series. Journal of Mathematical Analysis and Applications 2006, 318(1):333-351. 10.1016/j.jmaa.2005.06.007Simsek Y:
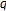 -Hardy-Berndt type sums associated with
-Hardy-Berndt type sums associated with 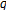 -Genocchi type zeta and
-Genocchi type zeta and  -functions. http://arxiv.org/abs/0710.5681v1
-functions. http://arxiv.org/abs/0710.5681v1Cenkci M, Can M, Kurt V:
 -adic interpolation functions and Kummer-type congruences for
-adic interpolation functions and Kummer-type congruences for 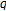 -twisted and
-twisted and 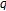 -generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004, 9(2):203-216.
-generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004, 9(2):203-216.Cangul IN, Kurt V, Simsek Y, Pak HK, Rim S-H:An invariant
 -adic
-adic 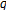 -integral associated with
-integral associated with 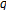 -Euler numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007, 14(1):8-14. 10.2991/jnmp.2007.14.1.2
-Euler numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007, 14(1):8-14. 10.2991/jnmp.2007.14.1.2Tsumura H:A note on
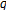 -analogues of the Dirichlet series and
-analogues of the Dirichlet series and 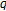 -Bernoulli numbers. Journal of Number Theory 1991, 39(3):251-256. 10.1016/0022-314X(91)90048-G
-Bernoulli numbers. Journal of Number Theory 1991, 39(3):251-256. 10.1016/0022-314X(91)90048-G
Acknowledgments
The first and third authors have been supported by the Scientific Research Project, Administration Akdeniz University. The second author has been supported by Uludag University Research Fund, Projects no. F2004/40 and F2008-31. The fourth author has been supported by National Institute for Mathematical Sciences Doryong-dong, Yuseong-gu, Daejeon. The authors express their sincere gratitude to referees for their suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Simsek, Y., Cangul, I.N., Kurt, V. et al. 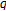 -Genocchi Numbers and Polynomials Associated with
-Genocchi Numbers and Polynomials Associated with 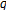 -Genocchi-Type
-Genocchi-Type  -Functions.
Adv Differ Equ 2008, 815750 (2007). https://doi.org/10.1155/2008/815750
-Functions.
Adv Differ Equ 2008, 815750 (2007). https://doi.org/10.1155/2008/815750
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/815750
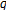 -genocchi Number and Polynomials
-genocchi Number and Polynomials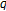 -genocchi Zeta and
-genocchi Zeta and  -Functions
-Functions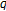 -Euler and Genocchi numbers. Proceedings of the Japan Academy. Series A 2001, 77(8):139-141. 10.3792/pjaa.77.139
-Euler and Genocchi numbers. Proceedings of the Japan Academy. Series A 2001, 77(8):139-141. 10.3792/pjaa.77.139 -Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8.
-Genocchi numbers and polynomials. Journal of Inequalities and Applications 2007, 2007:-8. -integers. Bulletin of the Korean Mathematical Society 2006, 43(3):611-617.
-integers. Bulletin of the Korean Mathematical Society 2006, 43(3):611-617. -integers. Advanced Studies in Contemporary Mathematics 2004, 9(1):15-18.
-integers. Advanced Studies in Contemporary Mathematics 2004, 9(1):15-18. -analog of the two-variable
-analog of the two-variable  -adic
-adic  -function. Russian Journal of Mathematical Physics 2005, 12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005, 12(2):186-196. -integers. Advanced Studies in Contemporary Mathematics 2006, 13(2):159-164.
-integers. Advanced Studies in Contemporary Mathematics 2006, 13(2):159-164. -analogue of twisted
-analogue of twisted  -series and
-series and  -twisted Euler numbers. Journal of Number Theory 2005, 110(2):267-278. 10.1016/j.jnt.2004.07.003
-twisted Euler numbers. Journal of Number Theory 2005, 110(2):267-278. 10.1016/j.jnt.2004.07.003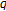 -integers. Journal of Applicable Functional Differential Equations 2006, 1(1):81-88.
-integers. Journal of Applicable Functional Differential Equations 2006, 1(1):81-88.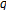 -Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005, 8(1):13-17.
-Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005, 8(1):13-17.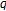 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic 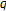 -integrals. Journal of Nonlinear Mathematical Physics 2007, 14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007, 14(1):15-27. 10.2991/jnmp.2007.14.1.3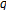 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007, 326(2):1458-1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007, 326(2):1458-1465. 10.1016/j.jmaa.2006.03.037 -adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985, 39(1):113-125. 10.2206/kyushumfs.39.113
-adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985, 39(1):113-125. 10.2206/kyushumfs.39.113 -Bernoulli numbers and polynomials associated with multiple
-Bernoulli numbers and polynomials associated with multiple 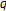 -zeta functions and basic
-zeta functions and basic 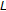 -series. Russian Journal of Mathematical Physics 2005, 12(2):241-268.
-series. Russian Journal of Mathematical Physics 2005, 12(2):241-268. -adic
-adic 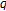 -integral on
-integral on 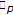 at
at 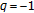 . Journal of Mathematical Analysis and Applications 2007, 331(2):779-792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007, 331(2):779-792. 10.1016/j.jmaa.2006.09.027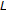 -function. Advanced Studies in Contemporary Mathematics 2005, 10(1):1-6.
-function. Advanced Studies in Contemporary Mathematics 2005, 10(1):1-6.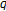 -
-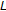 -series. Advanced Studies in Contemporary Mathematics 2005, 10(2):131-142.
-series. Advanced Studies in Contemporary Mathematics 2005, 10(2):131-142.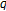 -Dedekind type sums related to
-Dedekind type sums related to 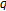 -zeta function and basic
-zeta function and basic  -series. Journal of Mathematical Analysis and Applications 2006, 318(1):333-351. 10.1016/j.jmaa.2005.06.007
-series. Journal of Mathematical Analysis and Applications 2006, 318(1):333-351. 10.1016/j.jmaa.2005.06.007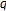 -Hardy-Berndt type sums associated with
-Hardy-Berndt type sums associated with 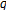 -Genocchi type zeta and
-Genocchi type zeta and  -functions.
-functions.  -adic interpolation functions and Kummer-type congruences for
-adic interpolation functions and Kummer-type congruences for 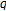 -twisted and
-twisted and 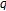 -generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004, 9(2):203-216.
-generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004, 9(2):203-216. -adic
-adic 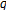 -integral associated with
-integral associated with 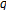 -Euler numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007, 14(1):8-14. 10.2991/jnmp.2007.14.1.2
-Euler numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007, 14(1):8-14. 10.2991/jnmp.2007.14.1.2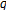 -analogues of the Dirichlet series and
-analogues of the Dirichlet series and 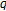 -Bernoulli numbers. Journal of Number Theory 1991, 39(3):251-256. 10.1016/0022-314X(91)90048-G
-Bernoulli numbers. Journal of Number Theory 1991, 39(3):251-256. 10.1016/0022-314X(91)90048-G