- Research Article
- Open access
- Published:
Existence and Multiple Solutions for Nonlinear Second-Order Discrete Problems with Minimum and Maximum
Advances in Difference Equations volume 2008, Article number: 586020 (2008)
Abstract
Consider the multiplicity of solutions to the nonlinear second-order discrete problems with minimum and maximum:  ,
,  ,
,  ,
,  , where
, where  are fixed numbers satisfying
are fixed numbers satisfying  are satisfying
are satisfying  ,
,  ,
, .
.
1. Introduction
Let  . Let
. Let

and for  , let
, let

Let

and for  , let
, let

It is clear that the above are norms on  and
and  , respectively, and that the finite dimensionality of these spaces makes them Banach spaces.
, respectively, and that the finite dimensionality of these spaces makes them Banach spaces.
In this paper, we discuss the nonlinear second-order discrete problems with minimum and maximum:


where  is a continuous function,
is a continuous function,  are fixed numbers satisfying
are fixed numbers satisfying  and
and  satisfying
satisfying  .
.
Functional boundary value problem has been studied by several authors [1–7]. But most of the papers studied the differential equations functional boundary value problem [1–6]. As we know, the study of difference equations represents a very important field in mathematical research [8–12], so it is necessary to investigate the corresponding difference equations with nonlinear boundary conditions.
Our ideas arise from [1, 3]. In 1993, Brykalov [1] discussed the existence of two different solutions to the nonlinear differential equation with nonlinear boundary conditions

where  is a bounded function, that is, there exists a constant
is a bounded function, that is, there exists a constant  , such that
, such that  . The proofs in [1] are based on the technique of monotone boundary conditions developed in [2]. From [1, 2], it is clear that the results of [1] are valid for functional differential equations in general form and for some cases of unbounded right-hand side of the equation (see [1, Remark 3 and (5)], [2, Remark 2 and (8)]).
. The proofs in [1] are based on the technique of monotone boundary conditions developed in [2]. From [1, 2], it is clear that the results of [1] are valid for functional differential equations in general form and for some cases of unbounded right-hand side of the equation (see [1, Remark 3 and (5)], [2, Remark 2 and (8)]).
In 1998, Staně k [3] worked on the existence of two different solutions to the nonlinear differential equation with nonlinear boundary conditions

where  satisfies the condition that there exists a nondecreasing function
satisfies the condition that there exists a nondecreasing function  satisfying
satisfying 
 , such that
, such that

It is not difficult to see that when we take  , (1.8) is to be (1.7), and
, (1.8) is to be (1.7), and  may not be bounded.
may not be bounded.
But as far as we know, there have been no discussions about the discrete problems with minimum and maximum in literature. So, we use the Borsuk theorem [13] to discuss the existence of two different solutions to the second-order difference equation boundary value problem (1.5), (1.6) when  satisfies
satisfies
(H 1)  is continuous, and there exist
is continuous, and there exist 
 , such that
, such that

where  .
.
In our paper, we assume  , if
, if  .
.
2. Preliminaries
Definition 2.1.
Let  be a functional.
be a functional.  is increasing if
is increasing if

Set

Remark 2.2.
Obviously,  belong to
belong to  . Now, if we take
. Now, if we take

then boundary condition (1.6) is equal to

So, in the rest part of this paper, we only deal with BVP (1.5), (2.4).
Lemma 2.3.
Suppose 
 . If there exist
. If there exist  , such that
, such that  , then
, then

Furthermore, one has

Proof.
Without loss of generality, we suppose  .
.
-
(i)
For
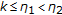 , we have
, we have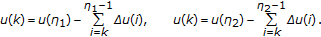 (2.7)
(2.7)Then
 (2.8)
(2.8)Furthermore,
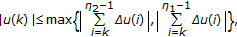 (2.9)
(2.9)which implies
 (2.10)
(2.10) -
(ii)
For
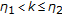 , we get
, we get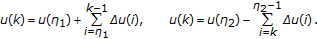 (2.11)
(2.11)Then
 (2.12)
(2.12)Furthermore,
 (2.13)
(2.13)which implies
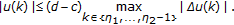 (2.14)
(2.14) -
(iii)
For
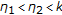 , we have
, we have  (2.15)
(2.15)Then
 (2.16)
(2.16)Furthermore,
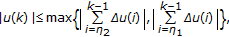 (2.17)
(2.17)which implies
 (2.18)
(2.18)In particular, it is not hard to obtain
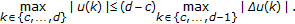 (2.19)
(2.19)
Similarly, we can obtain the following lemma.
Lemma 2.4.
Suppose 
 . If there exists
. If there exists  such that
such that  , then
, then

In particular, one has

Lemma 2.5.
Suppose  . If
. If  satisfies
satisfies

then there exist  , such that
, such that  .
.
Proof.
We only prove that there exists  , such that
, such that  , and the other can be proved similarly.
, and the other can be proved similarly.
Suppose  for
for  . Then
. Then  . Furthermore,
. Furthermore,  , which contradicts with
, which contradicts with  .
.
Define functional  by
by

Lemma 2.6.
Suppose  is a solution of (1.5) and
is a solution of (1.5) and  . Then
. Then

Proof.
Let

and  be the number of elements in
be the number of elements in  the number of elements in
the number of elements in  .
.
If  , then
, then  ; if
; if  , then
, then  . Equation (2.24) is obvious.
. Equation (2.24) is obvious.
Now, suppose  and
and  . It is easy to see that
. It is easy to see that

At first, we prove the inequality

Since  , by Lemma 2.5, there exist
, by Lemma 2.5, there exist  , such that
, such that  . Without loss of generality, we suppose
. Without loss of generality, we suppose  .
.
For any  , there exits
, there exits  satisfying one of the following cases:
satisfying one of the following cases:
Case 1.
 ,
,
Case 2.
 .
.
We only prove that (2.27) holds when Case 1 occurs, (if Case 2 occurs, it can be similarly proved).
If Case 1 holds, we divide the proof into two cases.
Subcase 1.1.
If  , without loss of generality, we suppose
, without loss of generality, we suppose  , then by Lemma 2.3, we have
, then by Lemma 2.3, we have

Combining this with

we have

At the same time, for  , we have
, we have  and
and

For  , we get
, we get

So, for  ,
,

Thus

Subcase 1.2 ( ).
).
Without loss of generality, we suppose  . Then
. Then  will be discussed in different situations.
will be discussed in different situations.
Subsubcase 1.2.1 ( ).
).
By Lemma 2.3 (we take 
 ), it is not difficult to see that
), it is not difficult to see that

For  , we have
, we have

So, we get

At the same time, for  ,
,

Combining this with  , we have
, we have

for  .
.
Also, for  , we have
, we have  and
and

Similarly, we get

By (2.39) and (2.41), for  ,
,

Then

Subsubcase 1.2.2 ( ).
).
By Lemma 2.3 (we take  ), it is easy to obtain that
), it is easy to obtain that

At the same time, for  ,
,

Together with  , we have
, we have

Thus

Case 1.2.3 ( ).
).
Without loss of generality, we suppose  (when
(when  , by Lemma 2.4, it can be proved similarly). Then from Lemma 2.3 (we take
, by Lemma 2.4, it can be proved similarly). Then from Lemma 2.3 (we take  ), it is not difficult to see that
), it is not difficult to see that

For  , we have
, we have

Together with  and
and  , for
, for  , we get
, we get

for  .
.
Also, for  , we have
, we have

This being combined with  , we get
, we get

From (2.50) and (2.52),

At last, from Case 1 and Case 2, we obtain

Then by the definition of  and (2.54),
and (2.54),

Similarly, we can prove

From (2.26), (2.55), and (2.56), the assertion is proved.
Remark 2.7.
It is easy to see that  is continuous, and
is continuous, and

Lemma 2.8.
Let  be a positive constant as in (2.3),
be a positive constant as in (2.3),  as in (2.3),
as in (2.3),  as in (2.23). Set
as in (2.23). Set

Define  :
:

Then

where  denotes Brouwer degree, and
denotes Brouwer degree, and  the identity operator on
the identity operator on  .
.
Proof.
Obviously,  is a bounded open and symmetric with respect to
is a bounded open and symmetric with respect to  subset of Banach space
subset of Banach space  .
.
Define 

For  ,
,

By Borsuk theorem, to prove  , we only need to prove that the following hypothesis holds.
, we only need to prove that the following hypothesis holds.
-
(a)
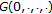 is an odd operator on
is an odd operator on  , that is,
, that is,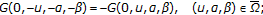 (2.63)
(2.63) -
(b)
 is a completely continuous operator;
is a completely continuous operator; -
(c)
 for
for 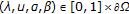 .
.First, we take
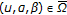 , then
, then

Thus  is asserted.
is asserted.
Second, we prove  .
.
Let  be a sequence. Then for each
be a sequence. Then for each  and the fact
and the fact 
 . The Bolzano-Weiestrass theorem and
. The Bolzano-Weiestrass theorem and  is finite dimensional show that, going if necessary to subsequences, we can assume
is finite dimensional show that, going if necessary to subsequences, we can assume 
 . Then
. Then

Since  and
and  are continuous,
are continuous,  is a continuous operator. Then
is a continuous operator. Then  is a completely continuous operator.
is a completely continuous operator.
At last, we prove (c).
Assume, on the contrary, that

for some  . Then
. Then



By (2.67) and Lemma 2.5 (take  ), there exists
), there exists  , such that
, such that  . Also from (2.67), we have
. Also from (2.67), we have  , then we get
, then we get


Case 1.
If  , then
, then  . Now, we claim
. Now, we claim  . In fact,
. In fact,  and (2.68) show that there exists
and (2.68) show that there exists  satisfying
satisfying  . This being combined with
. This being combined with  ,
,

So,  , which contradicts with
, which contradicts with  .
.
Case 2.
If  , then from (2.67),
, then from (2.67),  and the definition of
and the definition of  , we have
, we have

Together with (2.69), we get  , and
, and

Furthermore,  shows that
shows that  is strictly increasing. From (2.68) and Lemma 2.5, there exist
is strictly increasing. From (2.68) and Lemma 2.5, there exist  satisfying
satisfying  . Thus,
. Thus,  . It is not difficult to see that
. It is not difficult to see that

that is,

Similarly,  , then we get
, then we get  and
and  , which contradicts with
, which contradicts with  .
.
Case 3.
If  , then from (2.67), we get
, then from (2.67), we get  and
and

By (2.69), we have

If  , then
, then  . Furthermore,
. Furthermore,  , which contradicts with
, which contradicts with  .
.
If  , then
, then  . Furthermore,
. Furthermore,  , which contradicts with
, which contradicts with  .
.
If  , then
, then  a contradiction.
a contradiction.
Then (c) is proved.
From the above discussion, the conditions of Borsuk theorem are satisfied. Then, we get

Set

Similarly, we can prove

3. The Main Results
Theorem 3.1.
Suppose  holds. Then (1.5) and (1.6) have at least two different solutions when
holds. Then (1.5) and (1.6) have at least two different solutions when  and
and

Proof.
Let  . Consider the boundary conditions
. Consider the boundary conditions


Suppose  is a solution of (1.5). Then from Remark 2.7,
is a solution of (1.5). Then from Remark 2.7,

Now, if (1.5) and (3.2) have a solution  , then Lemma 2.6 and (3.2) show that
, then Lemma 2.6 and (3.2) show that  and
and

So,  is a solution of (1.5) and (2.4), that is,
is a solution of (1.5) and (2.4), that is,  is a solution of (1.5) and (1.6).
is a solution of (1.5) and (1.6).
Similarly, if (1.5), (3.3) have a solution  , then
, then  and
and

So,  is a solution of (1.5) and (2.4).
is a solution of (1.5) and (2.4).
Furthermore, since  and
and  .
.
Next, we need to prove BVPs (1.5), (3.2), and (1.5) and (3.3) have solutions, respectively.
Set

Define operator  ,
,

Obviously,

Consider the parameter equation

Now, we prove (3.10) has a solution, when  .
.
By Lemma 2.8,  . Now we prove the following hypothesis.
. Now we prove the following hypothesis.
-
(a)
 is a completely continuous operator;
is a completely continuous operator; -
(b)
 (3.11)
(3.11)
Since  is finite dimensional,
is finite dimensional,  is a completely continuous operator.
is a completely continuous operator.
Suppose (b) is not true. Then,

for some  . Then
. Then



From (3.13),  is a solution of second-order difference equation
is a solution of second-order difference equation  . By Remark 2.7,
. By Remark 2.7,  . And from (3.14), there exist
. And from (3.14), there exist  , such that
, such that  . Now, we can prove it in two cases.
. Now, we can prove it in two cases.
Case 1.
If there exists  , such that
, such that  , then
, then
-
(i)
for all
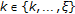 ,
,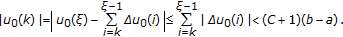 (3.16)
(3.16) -
(ii)
For all
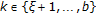 ,
,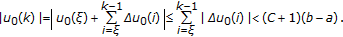 (3.17)
(3.17)
Case 2.
If  ,
,  . Set
. Set

-
(i)
For
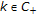 , if
, if 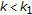 , then
, then (3.19)
(3.19)that is,
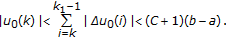 (3.20)
(3.20)For
 ,
,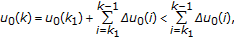 (3.21)
(3.21)then
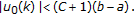 (3.22)
(3.22) -
(ii)
Similarly, we can prove
 for
for 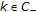 .
.Combining Case 1 with Case 2, we get
 (3.23)
(3.23)
Moreover,  , so,
, so,

which contradicts with  .
.
Similarly, consider the operator  ,
,

we can obtain a solution of BVP (1.5) and (3.3).
Theorem 3.2.
Suppose  holds. Then (1.5) and (1.6) have at least two different solutions when
holds. Then (1.5) and (1.6) have at least two different solutions when  and
and

Proof.
Obviously,  . Set
. Set

Then  Define continuous function
Define continuous function  ,
,

Then

Set  . Then
. Then  satisfies
satisfies  .
.
By Theorem 3.1,


have at least two difference solutions  . Since
. Since  is a solution of (3.30), if and only if
is a solution of (3.30), if and only if  is a solution of (1.5), we see that
is a solution of (1.5), we see that

are two different solutions of (1.5) and (2.4), then  are the two different solutions of (1.5) and (1.6).
are the two different solutions of (1.5) and (1.6).
References
Brykalov SA: Solutions with a prescribed minimum and maximum. Differencial'nye Uravnenija 1993, 29(6):938-942. translation in Differential Equations, vol. 29, no. 6, pp. 802–805, 1993
Brykalov SA: Solvability of problems with monotone boundary conditions. Differencial'nye Uravnenija 1993, 29(5):744-750. translation in Differential Equations, vol. 29, no. 5, pp. 633–639, 1993
Stančk S: Multiplicity results for second order nonlinear problems with maximum and minimum. Mathematische Nachrichten 1998, 192(1):225-237. 10.1002/mana.19981920113
Staněk S: Multiplicity results for functional boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(5):2617-2628. 10.1016/S0362-546X(97)00215-0
Whyburn WM: Differential equations with general boundary conditions. Bulletin of the American Mathematical Society 1942, 48: 692-704. 10.1090/S0002-9904-1942-07760-3
Ma R, Castaneda N: Existence of solutions of boundary value problems for second order functional differential equations. Journal of Mathematical Analysis and Applications 2004, 292(1):49-59. 10.1016/j.jmaa.2003.11.044
Cabada A:Extremal solutions for the difference
 -Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601.
-Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601.Ma R: Nonlinear discrete Sturm-Liouville problems at resonance. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(11):3050-3057. 10.1016/j.na.2006.09.058
Ma R: Bifurcation from infinity and multiple solutions for some discrete Sturm-Liouville problems. Computers & Mathematics with Applications 2007, 54(4):535-543. 10.1016/j.camwa.2007.03.001
Ma R, Luo H, Gao C: On nonresonance problems of second-order difference systems. Advances in Difference Equations 2008, 2008:-11.
Sun J-P: Positive solution for first-order discrete periodic boundary value problem. Applied Mathematics Letters 2006, 19(11):1244-1248. 10.1016/j.aml.2006.01.007
Gao C:Existence of solutions to
 -Laplacian difference equations under barrier strips conditions. Electronic Journal of Differential Equations 2007, 2007(59):1-6.
-Laplacian difference equations under barrier strips conditions. Electronic Journal of Differential Equations 2007, 2007(59):1-6.Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Acknowledgments
This work was supported by the NSFC (Grant no. 10671158), the NSF of Gansu Province (Grant no. 3ZS051-A25-016), NWNU-KJCXGC, the Spring-sun Program (no. Z2004-1-62033), SRFDP (Grant no. 20060736001), and the SRF for ROCS, SEM (2006[311]).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ma, R., Gao, C. Existence and Multiple Solutions for Nonlinear Second-Order Discrete Problems with Minimum and Maximum. Adv Differ Equ 2008, 586020 (2008). https://doi.org/10.1155/2008/586020
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/586020
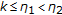 , we have
, we have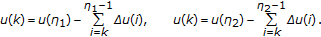

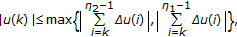

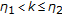 , we get
, we get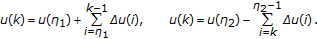


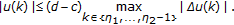
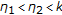 , we have
, we have 

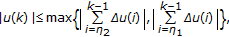

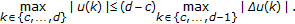
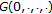 is an odd operator on
is an odd operator on  , that is,
, that is,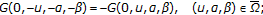
 is a completely continuous operator;
is a completely continuous operator; for
for 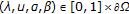 .
.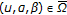 , then
, then is a completely continuous operator;
is a completely continuous operator;
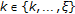 ,
,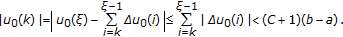
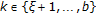 ,
,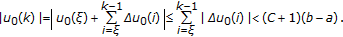
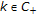 , if
, if 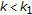 , then
, then
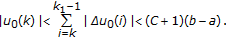
 ,
,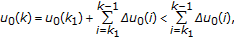
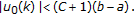
 for
for 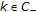 .
.
 -Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601.
-Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601. -Laplacian difference equations under barrier strips conditions. Electronic Journal of Differential Equations 2007, 2007(59):1-6.
-Laplacian difference equations under barrier strips conditions. Electronic Journal of Differential Equations 2007, 2007(59):1-6.