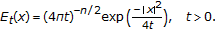- Research Article
- Open access
- Published:
A Functional Equation of Aczél and Chung in Generalized Functions
Advances in Difference Equations volume 2008, Article number: 147979 (2009)
Abstract
We consider an  -dimensional version of the functional equations of Aczél and Chung in the spaces of generalized functions such as the Schwartz distributions and Gelfand generalized functions. As a result, we prove that the solutions of the distributional version of the equation coincide with those of classical functional equation.
-dimensional version of the functional equations of Aczél and Chung in the spaces of generalized functions such as the Schwartz distributions and Gelfand generalized functions. As a result, we prove that the solutions of the distributional version of the equation coincide with those of classical functional equation.
1. Introduction
In [1], Aczél and Chung introduced the following functional equation:

where  and
and  for
for  . Under the natural assumptions that
. Under the natural assumptions that  and
and  are linearly independent, and
are linearly independent, and  ,
,  for all
for all  ,
,  , it was shown that the locally integrable solutions of (1.1) are exponential polynomials, that is, the functions of the form
, it was shown that the locally integrable solutions of (1.1) are exponential polynomials, that is, the functions of the form

where  and
and  's are polynomials for all
's are polynomials for all  .
.
In this paper, we introduce the following  -dimensional version of the functional equation (1.1) in generalized functions:
-dimensional version of the functional equation (1.1) in generalized functions:

where  (resp.,
(resp.,  ), and
), and  denotes the pullback,
denotes the pullback,  denotes the tensor product of generalized functions, and
denotes the tensor product of generalized functions, and  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . As in [1], we assume that
. As in [1], we assume that  and
and  for all
for all  ,
,  ,
,  .
.
In [2], Baker previously treated (1.3). By making use of differentiation of distributions which is one of the most powerful advantages of the Schwartz theory, and reducing (1.3) to a system of differential equations, he showed that, for the dimension  , the solutions of (1.3) are exponential polynomials. We refer the reader to [2–6] for more results using this method of reducing given functional equations to differential equations.
, the solutions of (1.3) are exponential polynomials. We refer the reader to [2–6] for more results using this method of reducing given functional equations to differential equations.
In this paper, by employing tensor products of regularizing functions as in [7, 8], we consider the regularity of the solutions of (1.3) and prove in an elementary way that (1.3) can be reduced to the classical equation (1.1) of smooth functions. This method can be applied to prove the Hyers-Ulam stability problem for functional equation in Schwartz distribution [7, 8]. In the last section, we consider the Hyers-Ulam stability of some related functional equations. For some elegant results on the classical Hyers-Ulam stability of functional equations, we refer the reader to [6, 9–21].
2. Generalized Functions
In this section, we briefly introduce the spaces of generalized functions such as the Schwartz distributions, Fourier hyperfunctions, and Gelfand generalized functions. Here we use the following notations:  ,
,  ,
,  ,
,  , and
, and  , for
, for  ,
,  , where
, where  is the set of nonnegative integers and
is the set of nonnegative integers and  .
.
Definition 2.1.
A distribution  is a linear functional on
is a linear functional on  of infinitely differentiable functions on
of infinitely differentiable functions on  with compact supports such that for every compact set
with compact supports such that for every compact set  there exist constants
there exist constants  and
and  satisfying
satisfying

for all  with supports contained in
with supports contained in  . One denotes by
. One denotes by  the space of the Schwartz distributions on
the space of the Schwartz distributions on  .
.
Definition 2.2.
For given  , one denotes by
, one denotes by  or
or  the space of all infinitely differentiable functions
the space of all infinitely differentiable functions  on
on  such that there exist positive constants
such that there exist positive constants  and
and  satisfying
satisfying

The topology on the space  is defined by the seminorms
is defined by the seminorms  in the left-hand side of (2.2), and the elements of the dual space
in the left-hand side of (2.2), and the elements of the dual space  of
of  are called Gelfand-Shilov generalized functions. In particular, one denotes
are called Gelfand-Shilov generalized functions. In particular, one denotes  by
by  and calls its elements Fourier hyperfunctions.
and calls its elements Fourier hyperfunctions.
It is known that if  and
and  , the space
, the space  consists of all infinitely differentiable functions
consists of all infinitely differentiable functions  on
on  that can be continued to an entire function on
that can be continued to an entire function on  satisfying
satisfying

for some  .
.
It is well known that the following topological inclusions hold:

We briefly introduce some basic operations on the spaces of the generalized functions.
Definition 2.3.
Let  . Then, the
. Then, the  th partial derivative
th partial derivative  of
of  is defined by
is defined by

for  . Let
. Let  . Then the multiplication
. Then the multiplication  is defined by
is defined by

Definition 2.4.
Let  ,
,  . Then, the tensor product
. Then, the tensor product  of
of  and
and  is defined by
is defined by

The tensor product  belongs to
belongs to  .
.
Definition 2.5.
Let  ,
,  , and let
, and let  be a smooth function such that for each
be a smooth function such that for each  the derivative
the derivative  is surjective. Then there exists a unique continuous linear map
is surjective. Then there exists a unique continuous linear map  such that
such that  , when
, when  is a continuous function. One calls
is a continuous function. One calls  the pullback of
the pullback of  by
by  and simply is denoted by
and simply is denoted by  .
.
The differentiations, pullbacks, and tensor products of Fourier hyperfunctions and Gelfand generalized functions are defined in the same way as distributions. For more details of tensor product and pullback of generalized functions, we refer the reader to [9, 22].
3. Main Result
We employ a function  such that
such that

Let  and
and  ,
,  . Then, for each
. Then, for each  ,
,  is well defined. We call
is well defined. We call  a regularizing function of the distribution
a regularizing function of the distribution  , since
, since  is a smooth function of
is a smooth function of  satisfying
satisfying  in the sense of distributions, that is, for every
in the sense of distributions, that is, for every  ,
,

Theorem 3.1.
Let  ,
,  ,
,  , be a solution of (1.3), and both
, be a solution of (1.3), and both  and
and  are linearly independent. Then,
are linearly independent. Then,  ,
,  ,
,  ,
,  ,
,  , where
, where  ,
,  ,
,  , a smooth solution of (1.1).
, a smooth solution of (1.1).
Proof.
By convolving the tensor product  in each side of (1.3), we have, for
in each side of (1.3), we have, for  ,
,

where  ,
,  ,
,  . Similarly we have for
. Similarly we have for  ,
,

Thus (1.3) is converted to the following functional equation:

where

for  ,
,  . We first prove that
. We first prove that  are smooth functions and equal to
are smooth functions and equal to  for all
for all  . Let
. Let

Then,

is a smooth function of  for each
for each  ,
,  , and
, and  is linearly independent. We may choose
is linearly independent. We may choose  ,
,  such that
such that  . Then, it follows from (3.5) that
. Then, it follows from (3.5) that

where  ,
,  . Putting (3.9) in (3.5), we have
. Putting (3.9) in (3.5), we have

where


Since  is a smooth function of
is a smooth function of  for each
for each  ,
,  , it follows from (3.11) that
, it follows from (3.11) that

is a smooth function of  for each
for each  ,
,  . Also, since
. Also, since  is linearly independent, it follows from (3.12) that
is linearly independent, it follows from (3.12) that

is linearly independent. Thus we can choose  ,
,  such that
such that  . Then, it follows from (3.10) that
. Then, it follows from (3.10) that

where  ,
,  . Putting (3.15) in (3.10), we have
. Putting (3.15) in (3.10), we have

where

By continuing this process, we obtain the following equations:

for all  , where
, where  ,
,  ,
,  ,
,

for all  , and
, and

By the induction argument, we have for each  ,
,

is a smooth function of  for each
for each  ,
,  . Thus, in view of (3.20),
. Thus, in view of (3.20),

is a smooth function. Furthermore,  converges to
converges to  locally uniformly, which implies that
locally uniformly, which implies that  in the sense of distributions, that is, for every
in the sense of distributions, that is, for every  ,
,

In view of (3.19) and the induction argument, for each  , we have
, we have

is a smooth function and  for all
for all  . Changing the roles of
. Changing the roles of  and
and  for
for  , we obtain, for each
, we obtain, for each  ,
,

is a smooth function and  . Finally, we show that for each
. Finally, we show that for each  ,
,  is equal to a smooth function. Letting
is equal to a smooth function. Letting  in (3.5), we have
in (3.5), we have

For each fixed  ,
,  , replacing
, replacing  by
by  , multiplying
, multiplying  and integrating with respect to
and integrating with respect to  , we have
, we have

where  for all
for all  ,
,  . Letting
. Letting  in (3.27), we have
in (3.27), we have

It is obvious that  is a smooth function. Also it follows from (3.27) that each
is a smooth function. Also it follows from (3.27) that each  ,
,  , converges locally and uniformly to the function
, converges locally and uniformly to the function  as
as  , which implies that the equality (3.28) holds in the sense of distributions. Finally, letting
, which implies that the equality (3.28) holds in the sense of distributions. Finally, letting  and
and  in (3.5) we see that
in (3.5) we see that  ,
,  are smooth solutions of (1.1). This completes the proof.
are smooth solutions of (1.1). This completes the proof.
Combined with the result of Aczél and Chung [1], we have the following corollary as a consequence of the above result.
Corollary 3.2.
Every solution  ,
,  ,
,  , of (1.3) for the dimension
, of (1.3) for the dimension  has the form of exponential polynomials.
has the form of exponential polynomials.
The result of Theorem 3.1 holds for  ,
,  ,
,  . Using the following
. Using the following  -dimensional heat kernel,
-dimensional heat kernel,

Applying the proof of Theorem 3.1, we get the result for the space of Gelfand generalized functions.
4. Hyers-Ulam Stability of Related Functional Equations
The well-known Cauchy equation, Pexider equation, Jensen equation, quadratic functional equation, and d'Alembert functional equation are typical examples of the form (1.1). For the distributional version of these equations and their stabilities, we refer the reader to [7, 8]. In this section, as well-known examples of (1.1), we introduce the following trigonometric differences:

where  . In 1990, Székelyhidi [23] has developed his idea of using invariant subspaces of functions defined on a group or semigroup in connection with stability questions for the sine and cosine functional equations. As the results, he proved that if
. In 1990, Székelyhidi [23] has developed his idea of using invariant subspaces of functions defined on a group or semigroup in connection with stability questions for the sine and cosine functional equations. As the results, he proved that if  ,
,  , is a bounded function on
, is a bounded function on  , then either there exist
, then either there exist  , not both zero, such that
, not both zero, such that  is a bounded function on
is a bounded function on  , or else
, or else  ,
,  , respectively. For some other elegant Hyers-Ulam stability theorems, we refer the reader to [6, 9–21].
, respectively. For some other elegant Hyers-Ulam stability theorems, we refer the reader to [6, 9–21].
By generalizing the differences (4.1), we consider the differences

and investigate the behavior of  satisfying the inequality
satisfying the inequality  for each
for each  , where
, where  ,
,  ,
,  ,
,  denotes the pullback,
denotes the pullback,  denotes the tensor product of generalized functions as in Theorem 3.1, and
denotes the tensor product of generalized functions as in Theorem 3.1, and  means that
means that  for all
for all  .
.
As a result, we obtain the following theorems.
Theorem 4.1.
Let  satisfy
satisfy  . Then,
. Then,  and
and  satisfy one of the following items:
satisfy one of the following items:
-
(i)
 ,
,  : arbitrary,
: arbitrary, -
(ii)
 and
and  are bounded measurable functions,
are bounded measurable functions, -
(iii)
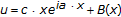 ,
, 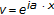 ,
, -
(iv)
 ,
,  ,
, -
(v)
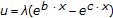 ,
, 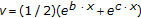 ,
, -
(vi)
 ,
, 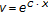 ,
,
where  ,
,  ,
,  , and
, and  is a bounded measurable function.
is a bounded measurable function.
Theorem 4.2.
Let  satisfy
satisfy  . Then,
. Then,  and
and  satisfy one of the following items:
satisfy one of the following items:
-
(i)
 and
and  are bounded measurable functions,
are bounded measurable functions, -
(ii)
 and
and  is a bounded measurable function,
is a bounded measurable function, -
(iii)
 ,
,  ,
, -
(iv)
 ,
, 
-
(v)
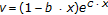 ,
, 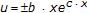 ,
, -
(vi)
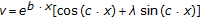 ,
, 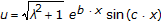 ,
,
where  ,
,  ,
,  , and
, and  is a bounded measurable function.
is a bounded measurable function.
Theorem 4.3.
Let  satisfy
satisfy  . Then,
. Then,  and
and  satisfy one of the following items:
satisfy one of the following items:
-
(i)
 and
and  is arbitrary,
is arbitrary, -
(ii)
 and
and  are bounded measurable functions,
are bounded measurable functions, -
(iii)
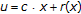 ,
, 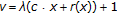 ,
, -
(iv)
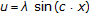 ,
, 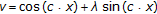 ,
,
for some  ,
,  and a bounded measurable function
and a bounded measurable function  .
.
Theorem 4.4.
Let  satisfy
satisfy  . Then,
. Then,  and
and  satisfy one of the following items:
satisfy one of the following items:
-
(i)
 and
and  are bounded measurable functions,
are bounded measurable functions, -
(ii)
 ,
, 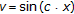 ,
, 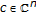 .
.For the proof of the theorems, we employ the
 -dimensional heat kernel
-dimensional heat kernel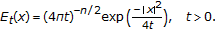 (4.3)
(4.3)
In view of (2.3), it is easy to see that for each  ,
,  belongs to the Gelfand-Shilov space
belongs to the Gelfand-Shilov space  . Thus the convolution
. Thus the convolution  is well defined and is a smooth solution of the heat equation
is well defined and is a smooth solution of the heat equation  in
in  and
and  in the sense of generalized functions for all
in the sense of generalized functions for all  .
.
Similarly as in the proof of Theorem 3.1, convolving the tensor product  of heat kernels and using the semigroup property
of heat kernels and using the semigroup property

of the heat kernels, we can convert the inequalities  ,
,  to the classical Hyers-Ulam stability problems, respectively,
to the classical Hyers-Ulam stability problems, respectively,

for the smooth functions  ,
,  . Proving the Hyers-Ulam stability problems for the inequalities (4.5) and taking the initial values of
. Proving the Hyers-Ulam stability problems for the inequalities (4.5) and taking the initial values of  and
and  as
as  , we get the results. For the complete proofs of the result, we refer the reader to [24].
, we get the results. For the complete proofs of the result, we refer the reader to [24].
Remark 4.5.
The referee of the paper has recommended the author to consider the Hyers-Ulam stability of the equations, which will be one of the most interesting problems in this field. However, the author has no idea of solving this question yet. Instead, Baker [25] proved the Hyers-Ulam stability of the equation

References
Aczél J, Chung JK: Integrable solutions of functional equations of a general type. Studia Scientiarum Mathematicarum Hungarica 1982, 17(1–4):51-67.
Baker JA: On a functional equation of Aczél and Chung. Aequationes Mathematicae 1993, 46(1-2):99-111. 10.1007/BF01834001
Baker JA: Distributional methods for functional equations. Aequationes Mathematicae 2001, 62(1-2):136-142.
Deeba E, Koh EL, Sahoo PK, Xie S: On a distributional analog of a sum form functional equation. Acta Mathematica Hungarica 1998, 78(4):333-344. 10.1023/A:1006551410698
Deeba E, Xie S: Distributional analog of a functional equation. Applied Mathematics Letters 2003, 16(5):669-673. 10.1016/S0893-9659(03)00065-X
Deeba E, Sahoo PK, Xie S: On a class of functional equations in distribution. Journal of Mathematical Analysis and Applications 1998, 223(1):334-346. 10.1006/jmaa.1998.5995
Chung J: Stability of approximately quadratic Schwartz distributions. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(1):175-186. 10.1016/j.na.2006.05.005
Chung J: A distributional version of functional equations and their stabilities. Nonlinear Analysis: Theory, Methods & Applications 2005, 62(6):1037-1051. 10.1016/j.na.2005.04.016
Häormander L: The Analysis of Linear Partial Differential Operators I. Springer, Berlin, Germany; 1983.
Gavruta P: An answer to a question of John M. Rassias concerning the stability of Cauchy equation. In Advances in Equations and Inequalities, Hadronic Mathematics. Hadronic Press, Palm Harbor, Fla, USA; 1999:67-71.
Jung S-M, Rassias JM: Stability of general Newton functional equations for logarithmic spirals. Advances in Difference Equations 2008, 2008:-5.
Kim H-M, Rassias JM, Cho Y-S: Stability problem of Ulam for Euler-Lagrange quadratic mappings. Journal of Inequalities and Applications 2007, 2007:-15.
Lee Y-S, Chung S-Y: Stability of Euler-Lagrange-Rassias equation in the spaces of generalized functions. Applied Mathematics Letters 2008, 21(7):694-700. 10.1016/j.aml.2007.07.022
Nakmahachalasint P: On the generalized Ulam-Gavruta-Rassias stability of mixed-type linear and Euler-Lagrange-Rassias functional equations. International Journal of Mathematics and Mathematical Sciences 2007, 2007:-10.
Pietrzyk A: Stability of the Euler-Lagrange-Rassias functional equation. Demonstratio Mathematica 2006, 39(3):523-530.
Rassias JM: On approximation of approximately linear mappings by linear mappings. Journal of Functional Analysis 1982, 46(1):126-130. 10.1016/0022-1236(82)90048-9
Rassias JM: On approximation of approximately linear mappings by linear mappings. Journal of Functional Analysis 1982, 46(1):126-130. 10.1016/0022-1236(82)90048-9
Rassias JM: On approximation of approximately linear mappings by linear mappings. Bulletin des Sciences Mathématiques. 2e Série 1984, 108(4):445-446.
Rassias JM: Solution of a problem of Ulam. Journal of Approximation Theory 1989, 57(3):268-273. 10.1016/0021-9045(89)90041-5
Rassias JM: Solution of a stability problem of Ulam. Discussiones Mathematicae 1992, 12: 95-103.
Rassias JM: On the stability of the Euler-Lagrange functional equation. Chinese Journal of Mathematics 1992, 20(2):185-190.
Gel'fand IM, Shilov GE: Generalized Functions. Vol. 2. Spaces of Fundamental and Generalized Functions. Academic Press, New York, NY, USA; 1968:x+261.
Székelyhidi L: The stability of the sine and cosine functional equations. Proceedings of the American Mathematical Society 1990, 110(1):109-115.
Chang J, Chung J: The stability of the sine and cosine functional equations in Schwartz distributions. Bulletin of the Korean Mathematical Society 2009, 46(1):87-97. 10.4134/BKMS.2009.46.1.087
Baker JA: A general functional equation and its stability. Proceedings of the American Mathematical Society 2005, 133(6):1657-1664. 10.1090/S0002-9939-05-07841-X
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chung, JY. A Functional Equation of Aczél and Chung in Generalized Functions. Adv Differ Equ 2008, 147979 (2009). https://doi.org/10.1155/2008/147979
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/147979
 ,
,  : arbitrary,
: arbitrary, and
and  are bounded measurable functions,
are bounded measurable functions,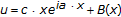 ,
, 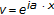 ,
, ,
,  ,
,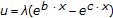 ,
, 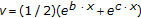 ,
, ,
, 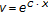 ,
, and
and  are bounded measurable functions,
are bounded measurable functions, and
and  is a bounded measurable function,
is a bounded measurable function, ,
,  ,
, ,
, 
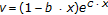 ,
, 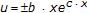 ,
,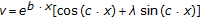 ,
, 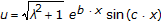 ,
, and
and  is arbitrary,
is arbitrary, and
and  are bounded measurable functions,
are bounded measurable functions,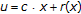 ,
, 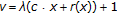 ,
,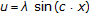 ,
, 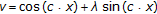 ,
, and
and  are bounded measurable functions,
are bounded measurable functions, ,
, 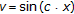 ,
, 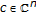 .
. -dimensional heat kernel
-dimensional heat kernel