- Research Article
- Open access
- Published:
On the Solutions of Systems of Difference Equations
Advances in Difference Equations volume 2008, Article number: 143943 (2008)
Abstract
We show that every solution of the following system of difference equations  ,
,  as well as of the system
as well as of the system  ,
,  is periodic with period 2
is periodic with period 2 if
if  (
( 2), and with period
2), and with period  if
if  (
( 2) where the initial values are nonzero real numbers for
2) where the initial values are nonzero real numbers for  .
.
1. Introduction
Difference equations appear naturally as discrete analogues and as numerical solutions of differential and delay differential equations having applications in biology, ecology, economy, physics, and so on [1]. So, recently there has been an increasing interest in the study of qualitative analysis of rational difference equations and systems of difference equations. Although difference equations are very simple in form, it is extremely difficult to understand thoroughly the behaviors of their solutions. (see [1–11] and the references cited therein).
Papaschinopoulos and Schinas [9, 10] studied the behavior of the positive solutions of the system of two Lyness difference equations

where  are positive constants and the initial values
are positive constants and the initial values  are positive.
are positive.
In [2] Camouzis and Papaschinopoulos studied the behavior of the positive solutions of the system of two difference equations

where the initial values 
 are positive numbers and
are positive numbers and  is a positive integer.
is a positive integer.
Moreover, Çinar [3] investigated the periodic nature of the positive solutions of the system of difference equations

where the initial values  are positive real numbers.
are positive real numbers.
Also, Özban [7] investigated the periodic nature of the solutions of the system of rational difference equations

where  is a nonnegative integer,
is a nonnegative integer,  is a positive integer, and the initial values
is a positive integer, and the initial values  are positive real numbers.
are positive real numbers.
In [12] Irćianin and Stević studied the positive solution of the following two systems of di¤erence equations

where  fixed.
fixed.
In [11] Papaschinopoulos et al. studied the system of difference equations

where  (for
(for  are positive constants,
are positive constants,  is an integer, and the initial values
is an integer, and the initial values  (for
(for  are positive real numbers.
are positive real numbers.
It is well known that all well-defined solutions of the difference equation

are periodic with period two. Motivated by (1.8), we investigate the periodic character of the following two systems of difference equations:


which can be considered as a natural generalizations of (1.8).
In order to prove main results of the paper we need an auxiliary result which is contained in the following simple lemma from number theory. Let  denote the greatest common divisor of the integers
denote the greatest common divisor of the integers  and
and 
Lemma 1.1.
Let  and
and  then the numbers
then the numbers  (or
(or  ) for
) for  satisfy the following property:
satisfy the following property:

Proof.
Suppose the contrary, then we have  for some
for some 
Since  it follows that
it follows that  is a divisor of
is a divisor of  On the other hand, since
On the other hand, since  we have
we have  which is a contradiction.
which is a contradiction.
Remark 1.2.
From Lemma 1.1 we see that the rests  for
for  of the numbers
of the numbers  for
for  obtained by dividing the numbers
obtained by dividing the numbers  by
by  , are mutually different, they are contained in the set
, are mutually different, they are contained in the set  , make a permutation of the ordered set
, make a permutation of the ordered set  , and finally
, and finally  is the first number of the form
is the first number of the form  such that
such that 
2. The Main Results
In this section, we formulate and prove the main results in this paper.
Theorem 2.1.
Consider (1.9) where  Then the following statements are true:
Then the following statements are true:
(a)if  , then every solution of (1.9) is periodic with period 2k,
, then every solution of (1.9) is periodic with period 2k,
(b)if  , then every solution of (1.9) is periodic with period k.
, then every solution of (1.9) is periodic with period k.
Proof.
First note that the system is cyclic. Hence it is enough to prove that the sequence  satisfies conditions (a) and (b) in the corresponding cases.
satisfies conditions (a) and (b) in the corresponding cases.
Further, note that for every  system (1.9) is equivalent to a system of
system (1.9) is equivalent to a system of  difference equations of the same form, where
difference equations of the same form, where

On the other hand, we have

(a)Let  for
for  be the rests mentioned in Remark 1.2. Then from (2.2) and Lemma 1.1 we obtain that
be the rests mentioned in Remark 1.2. Then from (2.2) and Lemma 1.1 we obtain that

Using (2.1) for sufficently large  we obtain that (2.3) is equivalent to (here we use the condition
we obtain that (2.3) is equivalent to (here we use the condition  )
)

From this and since by Lemma 1.1 the numbers  are pairwise different, the result follows in this case.
are pairwise different, the result follows in this case.
(b)Let  for some
for some  By (2.1) we have
By (2.1) we have

which yields the result.
Remark 2.2.
In order to make the proof of Theorem 2.1 clear to the reader, we explain what happens in the cases  and
and  .
.
For  , system (1.9) is equivalent to the system
, system (1.9) is equivalent to the system

where we consider that

From this and (2.2), we have

Using again (2.2), we get  which means that the sequence
which means that the sequence  is periodic with period equal to 2. If
is periodic with period equal to 2. If  , system (1.9) is equivalent to system (2.6) where we consider that
, system (1.9) is equivalent to system (2.6) where we consider that  , and
, and  Using this and (2.2) subsequently, it follows that
Using this and (2.2) subsequently, it follows that

that is, the sequence  is periodic with period 6.
is periodic with period 6.
Remark 2.3.
The fact that every solution of (1.8) is periodic with period two can be considered as the case  in Theorem 2.1, that is, we can take that
in Theorem 2.1, that is, we can take that

Similarly to Theorem 2.1, using Lemma 1.1 with  for
for  the following theorem can be proved.
the following theorem can be proved.
Theorem 2.4.
Consider (1.10) where  Then the following statements are true:
Then the following statements are true:
(a)if  , then every solution of (1.10) is periodic with period 2k,
, then every solution of (1.10) is periodic with period 2k,
(b)if  , then every solution of (1.10) is periodic with period k.
, then every solution of (1.10) is periodic with period k.
Proof.
First note that the system is cyclic. Hence, it is enough to prove that the sequence  satisfies conditions (a) and (b) in the corresponding cases.
satisfies conditions (a) and (b) in the corresponding cases.
Indeed, similarly to (2.2), we have

(a)Let  for
for  be the rests mentioned in Remark 1.2. Then from (2.11) and Lemma 1.1 we obtain that
be the rests mentioned in Remark 1.2. Then from (2.11) and Lemma 1.1 we obtain that

Using (2.1) for sufficiently large  we obtain that (2.12) is equivalent to (here we use the condition
we obtain that (2.12) is equivalent to (here we use the condition  )
)

From this and since by Lemma 1.1 the numbers  are pairwise different, the result follows in this case.
are pairwise different, the result follows in this case.
(b)Let  for some
for some  By (2.1) we have
By (2.1) we have

which yields the result.
Corollary 2.5.
Let  be solutions of (1.9) with the initial values
be solutions of (1.9) with the initial values  Assume that
Assume that

then all solutions of (1.9) are positive.
Proof.
We consider solutions of (1.9) with the initial values  satisfying (2.15). If
satisfying (2.15). If  , then from (1.9) and (2.15), we have
, then from (1.9) and (2.15), we have

for  and
and  .
.
If  , then from (1.9) and (2.15), we have
, then from (1.9) and (2.15), we have

for  and
and  .
.
From (2.16) and (2.17), all solutions of (1.9) are positive.
Corollary 2.6.
Let  be solutions of (1.9) with the initial values
be solutions of (1.9) with the initial values  . Assume that
. Assume that

then  are positive,
are positive,  are negative for all
are negative for all 
Proof.
From (2.16), (2.17), and (2.18), the proof is clear.
Corollary 2.7.
Let  be solutions of (1.9) with the initial values
be solutions of (1.9) with the initial values  . Assume that
. Assume that

then  are negative,
are negative,  are positive for all
are positive for all 
Proof.
From (2.16), (2.17), and (2.19), the proof is clear.
Corollary 2.8.
Let  be solutions of (1.9) with the initial values
be solutions of (1.9) with the initial values  , then the following statements are true (for all
, then the following statements are true (for all  and
and 
(i)if  then
then  and
and  ,
,
(ii)if  then
then  and
and 
(iii)if  then
then  and
and 
(iv)if  then
then  and
and  ,
,
(v)if  then
then  and
and  ,
,
(vi)if  then
then  and
and  .
.
Proof.
From (2.16) and (2.17), the proof is clear.
Corollary 2.9.
Let  be solutions of (1.10) with the initial values
be solutions of (1.10) with the initial values  . Assume that
. Assume that

then all solutions of (1.10) are positive.
Proof.
We consider solutions of (1.10) with the initial values  satisfying (2.20). If
satisfying (2.20). If  , then from (1.10) and (2.20), we have
, then from (1.10) and (2.20), we have

for  and
and  .
.
If  , then from (1.10) and (2.20), we have
, then from (1.10) and (2.20), we have

for  and
and  .
.
From (2.21) and (2.22), all solutions of (1.10) are positive.
Corollary 2.10.
Let  be solutions of (1.10) with the initial values
be solutions of (1.10) with the initial values  . Assume that
. Assume that

then  are positive,
are positive,  are negative for all
are negative for all 
Proof.
From (2.21), (2.22) and (2.23), the proof is clear.
Corollary 2.11.
Let  be solutions of (1.10) with the initial values
be solutions of (1.10) with the initial values  . Assume that
. Assume that

then  are negative,
are negative,  are positive for all
are positive for all 
Proof.
From (2.21), (2.22) and (2.24), the proof is clear.
Corollary 2.12.
Let  be solutions of (1.10) with the initial values
be solutions of (1.10) with the initial values  , then following statements are true (for all
, then following statements are true (for all  and
and 
(i)if  then
then  and
and  ,
,
(ii)if  then
then  and
and 
(iii)if  then
then  and
and 
(iv)if  then
then  and
and 
(v)if  then
then  and
and 
(vi)if  then
then  and
and 
Proof.
From (2.21), (2.22), and (2.24), the proof is clear.
Example 2.13.
Let  . Then the solutions of (1.9), with the initial values
. Then the solutions of (1.9), with the initial values  and
and  in its invertal of periodicity can be represented by Table 1.
in its invertal of periodicity can be represented by Table 1.
References
Papaschinopoulos G, Schinas CJ: On a system of two nonlinear difference equations. Journal of Mathematical Analysis and Applications 1998, 219(2):415–426. 10.1006/jmaa.1997.5829
Camouzis E, Papaschinopoulos G: Global asymptotic behavior of positive solutions on the system of rational difference equations
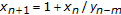 ,
, 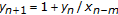 . Applied Mathematics Letters 2004, 17(6):733–737. 10.1016/S0893-9659(04)90113-9
. Applied Mathematics Letters 2004, 17(6):733–737. 10.1016/S0893-9659(04)90113-9Çinar C: On the positive solutions of the difference equation system
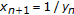 ,
, 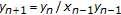 Applied Mathematics and Computation 2004, 158(2):303–305. 10.1016/j.amc.2003.08.073
Applied Mathematics and Computation 2004, 158(2):303–305. 10.1016/j.amc.2003.08.073Çinar C, Yalçinkaya İ: On the positive solutions of difference equation system
 ,
,  ,
,  International Mathematical Journal 2004, 5(5):521–524.
International Mathematical Journal 2004, 5(5):521–524.Clark D, Kulenović MRS: A coupled system of rational difference equations. Computers & Mathematics with Applications 2002, 43(6–7):849–867. 10.1016/S0898-1221(01)00326-1
Grove EA, Ladas G, McGrath LC, Teixeira CT: Existence and behavior of solutions of a rational system. Communications on Applied Nonlinear Analysis 2001, 8(1):1–25.
Özban AY: On the positive solutions of the system of rational difference equations
 ,
, 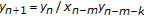 Journal of Mathematical Analysis and Applications 2006, 323(1):26–32. 10.1016/j.jmaa.2005.10.031
Journal of Mathematical Analysis and Applications 2006, 323(1):26–32. 10.1016/j.jmaa.2005.10.031Özban AY: On the system of rational difference equations
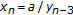 ,
, 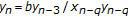 Applied Mathematics and Computation 2007, 188(1):833–837. 10.1016/j.amc.2006.10.034
Applied Mathematics and Computation 2007, 188(1):833–837. 10.1016/j.amc.2006.10.034Papaschinopoulos G, Schinas CJ: On the behavior of the solutions of a system of two nonlinear difference equations. Communications on Applied Nonlinear Analysis 1998, 5(2):47–59.
Papaschinopoulos G, Schinas CJ: Invariants for systems of two nonlinear difference equations. Differential Equations and Dynamical Systems 1999, 7(2):181–196.
Papaschinopoulos G, Schinas CJ, Stefanidou G: On a
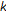 -order system of lyness-type difference equations. Advances in Difference Equations 2007, 2007:-13.
-order system of lyness-type difference equations. Advances in Difference Equations 2007, 2007:-13.Irićanin B, Stević S: Some systems of nonlinear difference equations of higher order with periodic solutions. Dynamics of Continuous, Discrete and Impulsive Systems, Series A Mathematical Analysis 2006, 13: 499–507.
Acknowledgment
The authors are grateful to the anonymous referees for their valuable suggestions that improved the quality of this study.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yalçinkaya, İ., Çinar, C. & Atalay, M. On the Solutions of Systems of Difference Equations. Adv Differ Equ 2008, 143943 (2008). https://doi.org/10.1155/2008/143943
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/143943
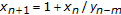 ,
, 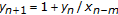 . Applied Mathematics Letters 2004, 17(6):733–737. 10.1016/S0893-9659(04)90113-9
. Applied Mathematics Letters 2004, 17(6):733–737. 10.1016/S0893-9659(04)90113-9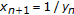 ,
, 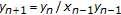 Applied Mathematics and Computation 2004, 158(2):303–305. 10.1016/j.amc.2003.08.073
Applied Mathematics and Computation 2004, 158(2):303–305. 10.1016/j.amc.2003.08.073 ,
,  ,
,  International Mathematical Journal 2004, 5(5):521–524.
International Mathematical Journal 2004, 5(5):521–524. ,
, 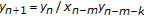 Journal of Mathematical Analysis and Applications 2006, 323(1):26–32. 10.1016/j.jmaa.2005.10.031
Journal of Mathematical Analysis and Applications 2006, 323(1):26–32. 10.1016/j.jmaa.2005.10.031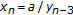 ,
, 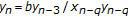 Applied Mathematics and Computation 2007, 188(1):833–837. 10.1016/j.amc.2006.10.034
Applied Mathematics and Computation 2007, 188(1):833–837. 10.1016/j.amc.2006.10.034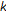 -order system of lyness-type difference equations. Advances in Difference Equations 2007, 2007:-13.
-order system of lyness-type difference equations. Advances in Difference Equations 2007, 2007:-13.