- Research Article
- Open access
- Published:
An Ultradiscrete Matrix Version of the Fourth Painlevé Equation
Advances in Difference Equations volume 2007, Article number: 096752 (2007)
Abstract
This paper is concerned with the matrix generalization of ultradiscrete systems. Specifically, we establish a matrix generalization of the ultradiscrete fourth Painlevé equation (ud-  ). Well-defined multicomponent systems that permit ultradiscretization are obtained using an approach that relies on a group defined by constraints imposed by the requirement of a consistent evolution of the systems. The ultradiscrete limit of these systems yields coupled multicomponent ultradiscrete systems that generalize ud-
). Well-defined multicomponent systems that permit ultradiscretization are obtained using an approach that relies on a group defined by constraints imposed by the requirement of a consistent evolution of the systems. The ultradiscrete limit of these systems yields coupled multicomponent ultradiscrete systems that generalize ud-  . The dynamics, irreducibility, and integrability of the matrix-valued ultradiscrete systems are studied.
. The dynamics, irreducibility, and integrability of the matrix-valued ultradiscrete systems are studied.
References
Painlevé P: Mémoire sur les équations différentielles dont l'intégrale générale est uniforme. Bulletin de la Société Mathématique de France 1900, 28: 201–261.
Grammaticos B, Ramani A: Discrete Painlevé equations: a review. In Discrete Integrable Systems, Lecture Notes in Phys.. Volume 644. Springer, Berlin, Germany; 2004:245–321.
Tokihiro T, Takahashi D, Matsukidaira J, Satsuma J: From soliton equations to integrable cellular automata through a limiting procedure. Physical Review Letters 1996,76(18):3247–3250. 10.1103/PhysRevLett.76.3247
Isojima S, Grammaticos B, Ramani A, Satsuma J: Ultradiscretization without positivity. Journal of Physics A 2006,39(14):3663–3672. 10.1088/0305-4470/39/14/011
Quispel GRW, Capel HW, Scully J: Piecewise-linear soliton equations and piecewise-linear integrable maps. Journal of Physics A 2001,34(11):2491–2503. 10.1088/0305-4470/34/11/337
Joshi N, Lafortune S: How to detect integrability in cellular automata. Journal of Physics A 2005,38(28):L499-L504. 10.1088/0305-4470/38/28/L03
Ormerod CM: Hypergeometric solutions to ultradiscrete Painlevé equations. preprint, 2006, http://arxiv.org/abs/nlin/0610048
Olver PJ, Sokolov VV: Integrable evolution equations on associative algebras. Communications in Mathematical Physics 1998,193(2):245–268. 10.1007/s002200050328
Kajiwara K, Noumi M, Yamada Y: A study on the fourth q -Painlevé equation. Journal of Physics A 2001,34(41):8563–8581. 10.1088/0305-4470/34/41/312
Sakai H: Rational surfaces associated with affine root systems and geometry of the Painlevé equations. Communications in Mathematical Physics 2001,220(1):165–229. 10.1007/s002200100446
Grammaticos B, Ohta Y, Ramani A, Takahashi D, Tamizhmani KM: Cellular automata and ultra-discrete Painlevé equations. Physics Letters A 1997,226(1–2):53–58. 10.1016/S0375-9601(96)00934-6
Mikhailov AV, Sokolov VV: Integrable ODEs on associative algebras. Communications in Mathematical Physics 2000,211(1):231–251. 10.1007/s002200050810
Balandin SP, Sokolov VV: On the Painlevé test for non-abelian equations. Physics Letters A 1998,246(3–4):267–272. 10.1016/S0375-9601(98)00336-3
Bobenko AI, Suris YuB: Integrable noncommutative equations on quad-graphs. The consistency approach. Letters in Mathematical Physics 2002,61(3):241–254. 10.1023/A:1021249131979
Field CM, Nijhoff FW, Capel HW: Exact solutions of quantum mappings from the lattice KdV as multi-dimensional operator difference equations. Journal of Physics A 2005,38(43):9503–9527. 10.1088/0305-4470/38/43/007
Joshi N, Ormerod CM: The general theory of linear difference equations over the invertible max-plus algebra. Stud. Appl. Math. 118 2007, (1):85–97.
Bunina EI, Mikhalëv AV: Automorphisms of the semigroup of invertible matrices with nonnegative elements. Fundamental'naya i Prikladnaya Matematika 2005,11(2):3–23.
Ramani A, Grammaticos B, Tamizhmani T, Tamizhmani KM: Special function solutions of the discrete Painlevé equations. Computers & Mathematics with Applications 2001,42(3–5):603–614.
Grammaticos B, Ramani A, Takenawa T: On the identity of two q -discrete Painlevé equations and their geometrical derivation. Advances in Difference Equations 2006, 2006: 11 pages.
Kajiwara K, Noumi M, Yamada Y: Discrete dynamical systems with
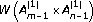 symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276
symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276Kajiwara K, Noumi M, Yamada Y: q -Painlevé systems arising from q -KP hierarchy. Letters in Mathematical Physics 2002,62(3):259–268. 10.1023/A:1022216308475
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Field, C.M., Ormerod, C.M. An Ultradiscrete Matrix Version of the Fourth Painlevé Equation. Adv Differ Equ 2007, 096752 (2007). https://doi.org/10.1155/2007/96752
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/96752
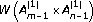 symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276
symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276