- Research Article
- Open access
- Published:
Nonlocal Impulsive Cauchy Problems for Evolution Equations
Advances in Difference Equations volume 2011, Article number: 784161 (2011)
Abstract
Of concern is the existence of solutions to nonlocal impulsive Cauchy problems for evolution equations. Combining the techniques of operator semigroups, approximate solutions, noncompact measures and the fixed point theory, new existence theorems are obtained, which generalize and improve some previous results since neither the Lipschitz continuity nor compactness assumption on the impulsive functions is required. An application to partial differential equations is also presented.
1. Introduction
Impulsive equations arise from many different real processes and phenomena which appeared in physics, chemical technology, population dynamics, biotechnology, medicine, and economics. They have in recent years been an object of investigations with increasing interest. For more information on this subject, see for instance, the papers (cf., e.g., [1–6]) and references therein.
On the other hand, Cauchy problems with nonlocal conditions are appropriate models for describing a lot of natural phenomena, which cannot be described using classical Cauchy problems. That is why in recent years they have been studied by many researchers (cf., e.g., [4, 7–12] and references therein).
In [4], the authors combined the two directions and studied firstly a class of nonlocal impulsive Cauchy problems for evolution equations by investigating the existence for mild (in generalized sense) solutions to the problems. In this paper, we study further the existence of solutions to the following nonlocal impulsive Cauchy problem for evolution equations:

where  is the infinitesimal generator of an analytic semigroup
is the infinitesimal generator of an analytic semigroup  and
and  is a real Banach space endowed with the norm
is a real Banach space endowed with the norm  ,
,

 ,
,  ,
,  ,
,  are given continuous functions to be specified later.
are given continuous functions to be specified later.
By going a new way, that is, by combining operator semigroups, the techniques of approximate solutions, noncompact measures, and the fixed point theory, we obtain new existence results for problem (1.1), which generalize and improve some previous theorems since neither the Lipschitz continuity nor compactness assumption on the impulsive functions is required in the present paper.
The organization of this work is as follows. In Section 2, we recall some definitions, and facts about fractional powers of operators, mild solutions and Hausdorff measure of noncompactness. In Section 3, we give the existence results for problem (1.1) when the nonlocal item and impulsive functions are only assumed to be continuous. In Section 4, we give an example to illustrate our abstract results.
2. Preliminaries
Let  be a real Banach space. We denote by
be a real Banach space. We denote by  the space of
the space of  -valued continuous functions on
-valued continuous functions on  with the norm
with the norm

and by  the space of
the space of  -valued Bochner integrable functions on
-valued Bochner integrable functions on  with the norm
with the norm  . Let
. Let

It is easy to check that  is a Banach space with the norm
is a Banach space with the norm

In this paper, for  , let
, let  and
and

Throughout this paper, we assume the following.
(H1) The operator  is the infinitesimal generator of a compact analytic semigroup
is the infinitesimal generator of a compact analytic semigroup  on Banach space
on Banach space  and
and  (the resolvent set of
(the resolvent set of  ).
).
In the remainder of this work,  .
.
Under the above conditions, it is possible to define the fractional power  ,
,  , of
, of  as closed linear operators. And it is known that the following properties hold.
as closed linear operators. And it is known that the following properties hold.
Theorem 2.1 (see [13, Pages 69–75]).
Let  and assume that (H1) holds. Then,
and assume that (H1) holds. Then,
-
(1)
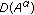 is a Banach space with the norm
is a Banach space with the norm  for
for 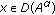 ,
, -
(2)
 for
for 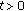 ,
, -
(3)
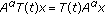 for
for 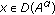 and
and 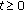 ,
, -
(4)
for every
 ,
,  is bounded on
is bounded on  and there exists
and there exists  such that
such that (2.5)
(2.5) -
(5)
 is a bounded linear operator in
is a bounded linear operator in  with
with  ,
, -
(6)
if
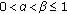 , then
, then 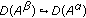 .
.
We denote by  that the Banach space
that the Banach space  endowed the graph norm from now on.
endowed the graph norm from now on.
Definition 2.2.
A function  is said to be a mild solution of (1.1) on
is said to be a mild solution of (1.1) on  if the function
if the function  is integrable on
is integrable on  for all
for all  and the following integral equation is satisfied:
and the following integral equation is satisfied:

To discuss the compactness of subsets of  , we let
, we let  ,
,  ,
,

For  , we denote by
, we denote by  the set
the set

 . Then it is easy to see that the following result holds.
. Then it is easy to see that the following result holds.
Lemma 2.3.
A set  is precompact in
is precompact in  if and only if the set
if and only if the set  is precompact in
is precompact in  for every
for every  .
.
Next, we recall that the Hausdorff measure of noncompactness  on each bounded subset
on each bounded subset  of Banach space
of Banach space  is defined by
is defined by

Some basic properties of  are given in the following Lemma.
are given in the following Lemma.
Lemma 2.4 (see [14]).
Let  be a real Banach space and let
be a real Banach space and let  be bounded. Then,
be bounded. Then,
-
(1)
 is precompact if and only if
is precompact if and only if  ;
; -
(2)
 , where
, where 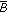 and
and 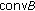 mean the closure and convex hull of
mean the closure and convex hull of  , respectively;
, respectively; -
(3)
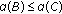 when
when  ;
; -
(4)
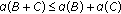 , where
, where  ;
; -
(5)
 ;
; -
(6)
 for any
for any  ;
; -
(7)
let
 be a Banach space and
be a Banach space and  Lipschitz continuous with constant
Lipschitz continuous with constant 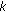 . Then
. Then  for all
for all 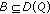 being bounded.
being bounded.
We note that a continuous map  is an
is an  -contraction if there exists a positive constant
-contraction if there exists a positive constant  such that
such that  for all bounded closed
for all bounded closed  .
.
Lemma 2.5 (see Darbo-Sadovskii's fixed point theorem in [14]).
If  is bounded closed and convex, and
is bounded closed and convex, and  is an
is an  -contraction, then the map
-contraction, then the map  has at least one fixed point in
has at least one fixed point in  .
.
3. Main Results
In this section, by using the techniques of approximate solutions and fixed points, we establish a result on the existence of mild solutions for the nonlocal impulsive problem (1.1) when the nonlocal item  and the impulsive functions
and the impulsive functions  are only assumed to be continuous in
are only assumed to be continuous in  and
and  , respectively.
, respectively.
In practical applications, the values of  for
for  near zero often do not affect
near zero often do not affect  . For example, it is the case when
. For example, it is the case when

So, to prove our main results, we introduce the following assumptions.
(H2) is a continuous function, and there is a
is a continuous function, and there is a  such that
such that  for any
for any  with
with  ,
,  . Moreover, there exist
. Moreover, there exist  such that
such that  for any
for any  .
.
(H3)There exists a  such that
such that  is a continuous function, and
is a continuous function, and  for any
for any  with
with  ,
,  . Moreover, there exist
. Moreover, there exist  such that
such that

for any  ,
,  , and
, and

for any  ,
,  .
.
(H4)The function  is continuous a.e.
is continuous a.e.  ; the function
; the function  is strongly measurable for all
is strongly measurable for all  . Moreover, for each
. Moreover, for each  , there exists a function
, there exists a function  such that
such that  for a.e.
for a.e.  and all
and all  , and
, and

(H5) is continuous for every
is continuous for every  , and there exist positive numbers
, and there exist positive numbers  such that
such that  for any
for any  and
and  .
.
We note that, by Theorem 2.1, there exist  and
and  such that
such that  and
and

For simplicity, in the following we set  and will substitute
and will substitute  by
by  below.
below.
Theorem 3.1.
Let (H1)–(H5) hold. Then the nonlocal impulsive Cauchy problem (1.1) has at least one mild solution on  , provided
, provided

To prove the theorem, we need some lemmas. Next, for  , we denote by
, we denote by  the maps
the maps  defined by
defined by

In addition, we introduce the decomposition  , where
, where

for  and
and  .
.
Lemma 3.2.
Assume that all the conditions in Theorem 3.1 are satisfied. Then for any  , the map
, the map  defined by (3.7) has at least one fixed point
defined by (3.7) has at least one fixed point  .
.
Proof.
To prove the existence of a fixed point for  , we will use Darbu-Sadovskii's fixed point theorem.
, we will use Darbu-Sadovskii's fixed point theorem.
Firstly, we prove that the map  is a contraction on
is a contraction on  . For this purpose, let
. For this purpose, let  . Then for each
. Then for each  and by condition (H3), we have
and by condition (H3), we have

Thus,

which implies that  is a contraction by condition (3.6).
is a contraction by condition (3.6).
Secondly, we prove that  ,
,  ,
,  are completely continuous operators. Let
are completely continuous operators. Let  be a sequence in
be a sequence in  with
with

in  . By the continuity of
. By the continuity of  with respect to the second argument, we deduce that for each
with respect to the second argument, we deduce that for each  ,
,  converges to
converges to  in
in  , and we have
, and we have

Then by the continuity of  ,
,  ,
,  , and using the dominated convergence theorem, we get
, and using the dominated convergence theorem, we get

in  , which implies that
, which implies that  are continuous on
are continuous on  .
.
Next, for the compactness of  we refer to the proof of [4, Theorem 3.1].
we refer to the proof of [4, Theorem 3.1].
For  and any bounded subset
and any bounded subset  of
of  , we have
, we have

which implies that  is relatively compact in
is relatively compact in  for every
for every  by the compactness of
by the compactness of  . On the other hand, for
. On the other hand, for  , we have
, we have

Since  is relatively compact in
is relatively compact in  , we conclude that
, we conclude that

which implies that  is equicontinuous on
is equicontinuous on  . Therefore,
. Therefore,  is a compact operator.
is a compact operator.
Now, we prove the compactness of  . For this purpose, let
. For this purpose, let

Note that

Thus according to Lemma 2.3, we only need to prove that

is precompact in  , as the remaining cases for
, as the remaining cases for  ,
,  , can be dealt with in the same way; here
, can be dealt with in the same way; here  is any bounded subset in
is any bounded subset in  . And, we recall that
. And, we recall that  ,
,  , which means that
, which means that

Thus, by the compactness of  , we know that
, we know that  is relatively compact in
is relatively compact in  for every
for every  .
.
Next, for  , we have
, we have

Thus, the set  is equicontinuous due to the compactness of
is equicontinuous due to the compactness of  and the strong continuity of operator
and the strong continuity of operator  . By the Arzela-Ascoli theorem, we conclude that
. By the Arzela-Ascoli theorem, we conclude that  is precompact in
is precompact in  . The same idea can be used to prove that
. The same idea can be used to prove that  is precompact for each
is precompact for each  . Therefore,
. Therefore,  is precompact in
is precompact in  , that is, the operator
, that is, the operator  is compact.
is compact.
Thus, for any bounded subset  , we have by Lemma 2.4,
, we have by Lemma 2.4,

Hence, the map  is an
is an  -contraction in
-contraction in  .
.
Now, in order to apply Lemma 2.5, it remains to prove that there exists a constant  such that
such that  . Suppose this is not true; then for each positive integer
. Suppose this is not true; then for each positive integer  , there are
, there are  and
and  such that
such that  . Then
. Then

Dividing on both sides by  and taking the lower limit as
and taking the lower limit as  , we obtain that
, we obtain that

This is a contradiction with inequality (3.6). Therefore, there exists  such that the mapping
such that the mapping  maps
maps  into itself. By Darbu-Sadovskii's fixed point theorem, the operator
into itself. By Darbu-Sadovskii's fixed point theorem, the operator  has at least one fixed point in
has at least one fixed point in  . This completes the proof.
. This completes the proof.
Lemma 3.3.
Assume that all the conditions in Theorem 3.1 are satisfied. Then the set  is precompact in
is precompact in  for all
for all  , where
, where

and  is the constant in (H2).
is the constant in (H2).
Proof.
The proof will be given in several steps. In the following  is a number in
is a number in  .
.
Step 1.
 is precompact in
is precompact in  .
.
For  , define
, define  by
by

For  , let
, let  ,
,  ,
,  ,
,  , and we define
, and we define  by
by

By condition (H3),  is well defined and for
is well defined and for  , we have
, we have

On the other hand, for  ,
,  , we have
, we have  ,
,  . So,
. So,

Now, for  , we have
, we have

By the compactness of  ,
,  , we get that
, we get that  is relatively compact in
is relatively compact in  for every
for every  and
and  is equicontinuous on
is equicontinuous on  , which implies that
, which implies that  is precompact in
is precompact in  .
.
By the same reasoning,  is precompact in
is precompact in  .
.
For  , we claim that
, we claim that  is Lipschitz continuous with constant
is Lipschitz continuous with constant  . In fact, (H3) implies that for every
. In fact, (H3) implies that for every  and
and  ,
,

that is,

Therefore,  is Lipschitz continuous with constant
is Lipschitz continuous with constant  .
.
Clearly,  is precompact in
is precompact in  , and so is
, and so is  in
in  .
.
Thus, by (3.29) and Lemma 2.4, we obtain

By (3.6),  , which implies
, which implies  . Consequently,
. Consequently,  is precompact in
is precompact in  .
.
Step 2.
 is precompact in
is precompact in  .
.
For  , let
, let

and define  by
by

By (H3),  is well defined and for
is well defined and for  , we have
, we have

So, for  ,
,  , we have
, we have

where

According to the proof of Step 1, we know that

are all precompact in  and
and  is Lipschitz continuous with constant
is Lipschitz continuous with constant  .
.
Next, we will show that  is precompact in
is precompact in  . Firstly, it is easy to see that
. Firstly, it is easy to see that  is precompact in
is precompact in  . Thus according to Lemma 2.3, it remains to prove that
. Thus according to Lemma 2.3, it remains to prove that

is precompact in  . And, we recall that
. And, we recall that  ,
,  , which means that
, which means that

By Step 1,  is precompact in
is precompact in  . Without loss of generality, we may suppose that
. Without loss of generality, we may suppose that

Therefore,  , as
, as  in
in  . Thus, by the continuity of
. Thus, by the continuity of  and
and  , we get
, we get

as  , which implies that
, which implies that  is relatively compact in
is relatively compact in  . And, for
. And, for  , by the compactness of
, by the compactness of  ,
,  ,
,  is also relatively compact in
is also relatively compact in  . Therefore,
. Therefore,  is relatively compact in
is relatively compact in  for every
for every  .
.
Next, for  , we have
, we have

Thus, the set  is equicontinuous on
is equicontinuous on  due to the compactness of
due to the compactness of  and the strong continuity of operator
and the strong continuity of operator  ,
,  . By the Arzela-Ascoli theorem, we conclude that
. By the Arzela-Ascoli theorem, we conclude that  is precompact in
is precompact in  . Therefore,
. Therefore,  is precompact in
is precompact in  .
.
Thus, by Lemma 2.4, we obtain

By (3.6),  , which implies
, which implies  . Consequently,
. Consequently,  is precompact in
is precompact in  .
.
Step 3.
The same idea can be used to prove the compactness of  in
in  for
for  , where
, where  . This completes the proof.
. This completes the proof.
Proof of Theorem 3.1.
For  ,
,  , let
, let

where  comes from the condition (H2). Then, by condition (H2),
comes from the condition (H2). Then, by condition (H2),  .
.
By Lemma 3.3, without loss of generality, we may suppose that  , as
, as  . Thus, by the continuity of
. Thus, by the continuity of  and
and  , we get
, we get

as  . Thus,
. Thus,

is precompact in  . Moreover,
. Moreover,  and
and  are both precompact in
are both precompact in  . And
. And  is Lipschitz continuous with constant
is Lipschitz continuous with constant  . Note that
. Note that

Therefore, by Lemma 2.4, we know that the set  is precompact in
is precompact in  . Without loss of generality, we may suppose that
. Without loss of generality, we may suppose that  in
in  . On the other hand, we also have
. On the other hand, we also have

Letting  in both sides, we obtain
in both sides, we obtain

which implies that  is a mild solution of the nonlocal impulsive problem (1.1). This completes the proof.
is a mild solution of the nonlocal impulsive problem (1.1). This completes the proof.
Remark 3.4.
From Lemma 3.3 and the above proof, it is easy to see that we can also prove Theorem 3.1 by showing that  is precompact in
is precompact in  .
.
The following results are immediate consequences of Theorem 3.5.
Theorem 3.5.
Assume (H1), (H3)–(H5) hold. If  , then the impulsive Cauchy problem (1.1) has at least one mild solution on
, then the impulsive Cauchy problem (1.1) has at least one mild solution on  , provided
, provided

Theorem 3.6.
Assume (H1), (H2), (H4), and (H5) hold. If  , then the nonlocal impulsive problem (1.1) has at least one mild solution on
, then the nonlocal impulsive problem (1.1) has at least one mild solution on  , provided
, provided  .
.
Theorem 3.7.
Assume (H1), (H4), and (H5) hold. If  , then the impulsive problem (1.1) has at least one mild solution on
, then the impulsive problem (1.1) has at least one mild solution on  , provided
, provided  .
.
Remark 3.8.
Theorems 3.5-3.6 are new even for many special cases discussed before, since neither the Lipschitz continuity nor compactness assumption on the impulsive functions is required.
4. Application
In this section, to illustrate our abstract result, we consider the following differential system:

where  ,
,  are given real numbers for
are given real numbers for  ,
,  , and
, and  and
and  are functions to be specified below.
are functions to be specified below.
To treat the above system, we take  with the norm
with the norm  and we consider the operator
and we consider the operator  defined by
defined by

with domain

The operator  is the infinitesimal generator of an analytic compact semigroup
is the infinitesimal generator of an analytic compact semigroup  on
on  . Moreover,
. Moreover,  has a discrete spectrum, the eigenvalues are
has a discrete spectrum, the eigenvalues are  ,
,  , with the corresponding normalized eigenvectors
, with the corresponding normalized eigenvectors  , and the following properties are satisfied.
, and the following properties are satisfied.
-
(a)
If
 , then
, then  .
. -
(b)
For each
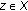 ,
,  . Moreover,
. Moreover, 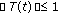 for all
for all 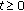 .
. -
(c)
For each
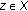 ,
, 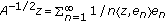 . In particular,
. In particular, 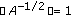 .
. -
(d)
 is given by
is given by  with the domain
with the domain 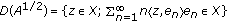 .
.
Assume the following.
-
(1)
The function
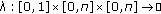 is continuously differential with
is continuously differential with  for
for  ,
,  , and there exists a real number
, and there exists a real number 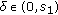 such that
such that 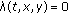 for
for 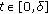 ,
, 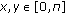 . Moreover,
. Moreover,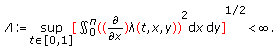 (4.4)
(4.4) -
(2)
For each
 ,
,  is continuous, and for each
is continuous, and for each 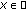 ,
, 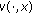 is measurable and, there exists a function
is measurable and, there exists a function  such that
such that  for a.e.
for a.e. 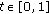 and all
and all 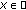 .
. -
(3)
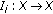 is a continuous function for each
is a continuous function for each  , and there exist positive numbers
, and there exist positive numbers 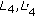 such that
such that 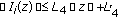 for any
for any  and
and 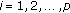 .
.
Define  and
and  , respectively, as follows. For
, respectively, as follows. For  ,
,

From the definition of  and assumption (1), it follows that
and assumption (1), it follows that

Thus, system (4.1) can be transformed into the abstract problem (1.1), and conditions (H2), (H3), (H4), and (H5) are satisfied with

If (3.6) holds (it holds when the related constants are small), then according to Theorem 3.1, the problem (4.1) has at least one mild solution in  .
.
References
Ahmed NU: Optimal feedback control for impulsive systems on the space of finitely additive measures. Publicationes Mathematicae Debrecen 2007,70(3-4):371-393.
Cardinali T, Rubbioni P: Impulsive semilinear differential inclusions: topological structure of the solution set and solutions on non-compact domains. Nonlinear Analysis: Theory, Methods & Applications 2008,69(1):73-84. 10.1016/j.na.2007.05.001
Eduardo Hernández M, Tanaka Aki SM: Global solutions for abstract impulsive differential equations. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1280-1290. 10.1016/j.na.2009.08.020
Liang J, Liu JH, Xiao T-J: Nonlocal impulsive problems for nonlinear differential equations in Banach spaces. Mathematical and Computer Modelling 2009,49(3-4):798-804. 10.1016/j.mcm.2008.05.046
Liu JH: Nonlinear impulsive evolution equations. Dynamics of Continuous, Discrete and Impulsive Systems 1999,6(1):77-85.
Rogovchenko YV: Impulsive evolution systems: main results and new trends. Dynamics of Continuous, Discrete and Impulsive Systems 1997,3(1):57-88.
Aizicovici S, Lee H: Nonlinear nonlocal Cauchy problems in Banach spaces. Applied Mathematics Letters 2005,18(4):401-407. 10.1016/j.aml.2004.01.010
Aizicovici S, Staicu V: Multivalued evolution equations with nonlocal initial conditions in Banach spaces. NoDEA. Nonlinear Differential Equations and Applications 2007,14(3-4):361-376. 10.1007/s00030-007-5049-5
Byszewski L, Lakshmikantham V: Theorem about the existence and uniqueness of a solution of a nonlocal abstract Cauchy problem in a Banach space. Applicable Analysis 1991,40(1):11-19. 10.1080/00036819008839989
Liang J, Liu J, Xiao T-J: Nonlocal Cauchy problems governed by compact operator families. Nonlinear Analysis: Theory, Methods & Applications 2004,57(2):183-189. 10.1016/j.na.2004.02.007
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
Xiao T-J, Liang J: Existence of classical solutions to nonautonomous nonlocal parabolic problems. Nonlinear Analysis, Theory, Methods and Applications 2005,63(5–7):e225-e232.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Banaś J, Goebel K: Measures of Noncompactness in Banach Spaces, Lecture Notes in Pure and Applied Mathematics. Volume 60. Marcel Dekker, New York, NY, USA; 1980:vi+97.
Acknowledgments
The authors would like to thank the referees for helpful comments and suggestions. J. Liang acknowledges support from the NSF of China (10771202) and the Specialized Research Fund for the Doctoral Program of Higher Education of China (2007035805). Z. Fan acknowledges support from the NSF of China (11001034) and the Research Fund for Shanghai Postdoctoral Scientific Program (10R21413700).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liang, J., Fan, Z. Nonlocal Impulsive Cauchy Problems for Evolution Equations. Adv Differ Equ 2011, 784161 (2011). https://doi.org/10.1155/2011/784161
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/784161
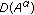 is a Banach space with the norm
is a Banach space with the norm  for
for 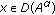 ,
, for
for 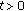 ,
,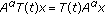 for
for 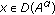 and
and 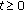 ,
, ,
,  is bounded on
is bounded on  and there exists
and there exists  such that
such that
 is a bounded linear operator in
is a bounded linear operator in  with
with  ,
,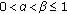 , then
, then 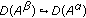 .
. is precompact if and only if
is precompact if and only if  ;
; , where
, where 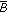 and
and 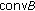 mean the closure and convex hull of
mean the closure and convex hull of  , respectively;
, respectively;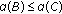 when
when  ;
;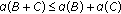 , where
, where  ;
; ;
; for any
for any  ;
; be a Banach space and
be a Banach space and  Lipschitz continuous with constant
Lipschitz continuous with constant 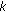 . Then
. Then  for all
for all 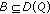 being bounded.
being bounded. , then
, then  .
.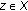 ,
,  . Moreover,
. Moreover, 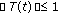 for all
for all 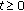 .
.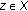 ,
, 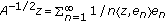 . In particular,
. In particular, 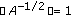 .
. is given by
is given by  with the domain
with the domain 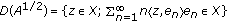 .
.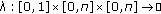 is continuously differential with
is continuously differential with  for
for  ,
,  , and there exists a real number
, and there exists a real number 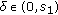 such that
such that 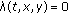 for
for 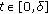 ,
, 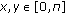 . Moreover,
. Moreover,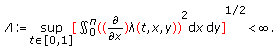
 ,
,  is continuous, and for each
is continuous, and for each 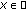 ,
, 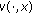 is measurable and, there exists a function
is measurable and, there exists a function  such that
such that  for a.e.
for a.e. 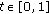 and all
and all 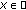 .
.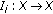 is a continuous function for each
is a continuous function for each  , and there exist positive numbers
, and there exist positive numbers 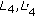 such that
such that 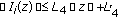 for any
for any  and
and  .
.