- Research Article
- Open access
- Published:
Oscillation for a Class of Second-Order Emden-Fowler Delay Dynamic Equations on Time Scales
Advances in Difference Equations volume 2010, Article number: 642356 (2010)
Abstract
By means of Riccati transformation technique, we establish some new oscillation criteria for the second-order Emden-Fowler delay dynamic equations  on a time scale
on a time scale  ; here
; here  is a quotient of odd positive integers with
is a quotient of odd positive integers with  and
and  as real-valued positive rd-continuous functions defined on
as real-valued positive rd-continuous functions defined on  . Our results in this paper not only extend the results given in Agarwal et al. (2005), Akin-Bohner et al. (2007) and Han et al. (2007) but also unify the results about oscillation of the second-order Emden-Fowler delay differential equation and the second-order Emden-Fowler delay difference equation.
. Our results in this paper not only extend the results given in Agarwal et al. (2005), Akin-Bohner et al. (2007) and Han et al. (2007) but also unify the results about oscillation of the second-order Emden-Fowler delay differential equation and the second-order Emden-Fowler delay difference equation.
1. Introduction
The theory of time scales, which has recently received a lot of attention, was introduced by Hilger in his Ph.D. Thesis in 1988 in order to unify continuous and discrete analysis (see Hilger [1]). Several authors have expounded on various aspects of this new theory; see the survey paper by Agarwal et al. [2] and references cited therein. A book on the subject of time scales, by Bohner and Peterson [3], summarizes and organizes much of the time scale calculus; we refer also to the last book by Bohner and Peterson [4] for advances in dynamic equations on time scales. For the notions used below, we refer to the next section that provides some basic facts on time scales extracted from Bohner and Peterson [3].
A time scale  is an arbitrary closed subset of the reals, and the cases when this time scale is equal to the reals or to the integers represent the classical theories of differential and of difference equations. Not only does the new theory of the so-called dynamic equations unify the theories of differential equations and difference equations, but also it extends these classical cases to cases in between, for example, to the so-called
is an arbitrary closed subset of the reals, and the cases when this time scale is equal to the reals or to the integers represent the classical theories of differential and of difference equations. Not only does the new theory of the so-called dynamic equations unify the theories of differential equations and difference equations, but also it extends these classical cases to cases in between, for example, to the so-called  difference equations when
difference equations when  which has important applications in quantum theory and can be applied on different types of time scales like
which has important applications in quantum theory and can be applied on different types of time scales like  , and
, and  the space of the harmonic numbers.
the space of the harmonic numbers.
Many other interesting time scales exist, and they give rise to plenty of applications, among them the study of population dynamic models which are discrete in season (and may follow a difference scheme with variable step-size or often modeled by continuous dynamic systems), die out, say in winter, while their eggs are incubating or dormant, and then in season again, hatching gives rise to a nonoverlapping population (see Bohner and Peterson [3]).
In recent years, there has been much research activity concerning the oscillation and nonoscillation of solutions of various equations on time scales, and we refer the reader to Akin-Bohner and Hoffacker [5, 6], Akin-Bohner et al. [7], Bohner and Saker [8], Erbe [9], Erbe et al. [10], Li et al. [11], and Saker [12, 13]. However, there are few results dealing with the oscillation of the solutions of delay dynamic equations on time scales [14–29].
Following this trend, in this paper, we consider a second-order nonlinear delay differential equation

For oscillation of the second-order delay dynamic equations, Agarwal et al. [14] considered the second-order delay dynamic equations on time scales

and established some sufficient conditions for oscillation of (1.2).
Zhang and Shanliang [29] studied the second-order nonlinear delay dynamic equations on time scales

and the second-order nonlinear dynamic equations on time scales

where  and
and  is continuous and nondecreasing
is continuous and nondecreasing  , and
, and  for
for  , and established the equivalence of the oscillation of (1.3) and (1.4). However, the results established in [29] are valid only when the graininess function
, and established the equivalence of the oscillation of (1.3) and (1.4). However, the results established in [29] are valid only when the graininess function  is bounded which is a restrictive condition. Also the restriction
is bounded which is a restrictive condition. Also the restriction  is required.
is required.
Şahiner [23] considered the second-order nonlinear delay dynamic equations on time scales

where  is continuous,
is continuous,  for
for  and
and  , and
, and  and obtained some sufficient conditions for oscillation of (1.5).
and obtained some sufficient conditions for oscillation of (1.5).
Han et al. [17] investigated the second-order Emden-Fowler delay dynamic equations on time scales

established some sufficient conditions for oscillation of (1.6), and extended the results given in [14].
Erbe et al. [28] considered the general nonlinear delay dynamic equations on time scales

where  and
and  are positive, real-valued rd-continuous functions defined on
are positive, real-valued rd-continuous functions defined on  ,
,  is rd-continuous,
is rd-continuous,  and
and  as
as  , and
, and  satisfies for some positive constant
satisfies for some positive constant  ,
,  for all nonzero
for all nonzero  , and extended the generalized Riccati transformation techniques in the time scales setting to obtain some new oscillation criteria which improve the results given by Şahiner [23] and Zhang and Shanliang [29].
, and extended the generalized Riccati transformation techniques in the time scales setting to obtain some new oscillation criteria which improve the results given by Şahiner [23] and Zhang and Shanliang [29].
Clearly, (1.2), (1.3), (1.5), (1.6), and (1.7) are different from (1.1). To develop the qualitative theory of delay dynamic equations on time scales, in this paper, we consider the second-order nonlinear delay dynamic equation on time scales (1.1).
As we are interested in oscillatory behavior, we assume throughout this paper that the given time scale  is unbounded above, that is, it is a time scale interval of the form
is unbounded above, that is, it is a time scale interval of the form  with
with  .
.
We assume that  is a quotient of odd positive integer,
is a quotient of odd positive integer,  and
and  are positive, real-valued rd-continuous functions defined on and
are positive, real-valued rd-continuous functions defined on and  ,
,  is a rd-continuous function such that
is a rd-continuous function such that  and
and  .
.
We shall also consider the two cases


By a solution of (1.1), we mean a nontrivial real-valued function  satisfying (1.1) for
satisfying (1.1) for  . A solution
. A solution  of (1.1) is called oscillatory if it is neither eventually positive nor eventually negative; otherwise, it is called nonoscillatory. Equation (1.1) is called oscillatory if all solutions are oscillatory. Our attention is restricted to those solutions
of (1.1) is called oscillatory if it is neither eventually positive nor eventually negative; otherwise, it is called nonoscillatory. Equation (1.1) is called oscillatory if all solutions are oscillatory. Our attention is restricted to those solutions  of (1.1) which exist on some half line
of (1.1) which exist on some half line  with
with  for any
for any  .
.
We note that if  , then
, then  , and (1.1) becomes the second-order Emden-Fowler delay differential equation
, and (1.1) becomes the second-order Emden-Fowler delay differential equation

If  , then
, then  and (1.1) becomes the second-order Emden-Fowler delay difference equation
and (1.1) becomes the second-order Emden-Fowler delay difference equation

In the case of  , (1.1) is the prototype of a wide class of nonlinear dynamic equations called Emden-Fowler superlinear dynamic equations, and if
, (1.1) is the prototype of a wide class of nonlinear dynamic equations called Emden-Fowler superlinear dynamic equations, and if  , then (1.1) is the prototype of dynamic equations called Emden-Fowler sublinear dynamic equations. It is interesting to study (1.1) because the continuous version, that is, (1.10), has several physical applications—see, for example, [1] —and when
, then (1.1) is the prototype of dynamic equations called Emden-Fowler sublinear dynamic equations. It is interesting to study (1.1) because the continuous version, that is, (1.10), has several physical applications—see, for example, [1] —and when  is a discrete variable as in (1.11), (1.1) also has important applications.
is a discrete variable as in (1.11), (1.1) also has important applications.
Numerous oscillation and nonoscillation criteria have been established for equations as (1.10) and (1.11); see, for example, [1, 30–36] and references therein.
In this paper, we intend to use the Riccati transformation technique for obtaining several oscillation criteria for (1.1). Our results in this paper not only extend the results given in Agarwal et al. [14] and Han et al. [17] but also unify the oscillation of the second-order Emden-Fowler delay differential equation and the second-order Emden-Fowler delay difference equation. Applications to equations to which previously known criteria for oscillation are not applicable are given.
This paper is organized as follows: in Section 2, we present the basic definitions and the theory of calculus on time scales. In Section 3, we apply a simple consequence of Kellers chain rule, devoted to the proof of the sufficient conditions for oscillation of all solutions of (1.1). In Section 4, some applications and examples are considered to illustrate the main results.
2. Some Preliminaries
A time scale  is an arbitrary nonempty closed subset of the real numbers
is an arbitrary nonempty closed subset of the real numbers  . Since we are interested in oscillatory behavior, we suppose that the time scale under consideration is not bounded above, that is, it is a time scale interval of the form
. Since we are interested in oscillatory behavior, we suppose that the time scale under consideration is not bounded above, that is, it is a time scale interval of the form  . On any time scale, we define the forward and backward jump operators by
. On any time scale, we define the forward and backward jump operators by

A point  is said to be left-dense if
is said to be left-dense if  , right-dense if
, right-dense if  , left-scattered if
, left-scattered if  , and right-scattered if
, and right-scattered if  . The graininess
. The graininess  of the time scale is defined by
of the time scale is defined by  .
.
For a function  (the range
(the range  of
of  may actually be replaced by any Banach space), the (delta) derivative is defined by
may actually be replaced by any Banach space), the (delta) derivative is defined by

if  is continuous at
is continuous at  and
and  is right-scattered. If
is right-scattered. If  is not right-scattered, then the derivative is defined by
is not right-scattered, then the derivative is defined by

provided this limit exists.
A function  is said to be rd-continuous if it is continuous at each right-dense point and if there exists a finite left limit in all left-dense points. The set of rd-continuous functions
is said to be rd-continuous if it is continuous at each right-dense point and if there exists a finite left limit in all left-dense points. The set of rd-continuous functions  is denoted by
is denoted by  .
.
 is said to be differentiable if its derivative exists. The set of functions
is said to be differentiable if its derivative exists. The set of functions  that are differentiable and whose derivative is rd-continuous function is denoted by
that are differentiable and whose derivative is rd-continuous function is denoted by  .
.
The derivative and the shift operator  are related by the formula
are related by the formula

Let  be a real-valued function defined on an interval
be a real-valued function defined on an interval  . We say that
. We say that  is increasing, decreasing, nondecreasing, and nonincreasing on
is increasing, decreasing, nondecreasing, and nonincreasing on  if
if  and
and  imply
imply  ,
,  ,
,  , and
, and  , respectively. Let
, respectively. Let  be a differentiable function on
be a differentiable function on  . Then
. Then  is increasing, decreasing, nondecreasing, and nonincreasing on
is increasing, decreasing, nondecreasing, and nonincreasing on  if
if  ,
,  ,
,  , and
, and  for all
for all  , respectively.
, respectively.
We will make use of the following product and quotient rules for the derivative of the product  and the quotient
and the quotient  of two differentiable functions
of two differentiable functions  and
and 


For  and a differentiable function
and a differentiable function  , the Cauchy integral of
, the Cauchy integral of  is defined by
is defined by

The integration by parts formula reads

and infinite integrals are defined as

In case  , we have
, we have

And in case  , we have
, we have

3. Main Results
In this section, we give some new oscillation criteria for (1.1). Since we are interested in oscillatory behavior, we will suppose that the time scale  under consideration is not bounded above, that is, it is a time scale interval of the form
under consideration is not bounded above, that is, it is a time scale interval of the form  . In order to prove our main results, we will use the formula
. In order to prove our main results, we will use the formula

where  is delta differentiable and eventually positive or eventually negative, which is a simple consequence of Keller's chain rule (see Bohner and Peterson [3, Theorem
is delta differentiable and eventually positive or eventually negative, which is a simple consequence of Keller's chain rule (see Bohner and Peterson [3, Theorem  ]). Also, we need the following auxiliary result.
]). Also, we need the following auxiliary result.
Lemma 3.1 (Şahiner [23, Lemma  ]).
]).
Suppose that the following conditions hold:
-
(H1)
 , where
, where  for some
for some  ;
; -
(H2)
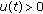 ,
,  and
and 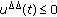 for
for  .
.
Then, for each  , there exists a constant
, there exists a constant  ,
,  , such that
, such that

Lemma 3.2.
Assume that (1.8) holds. Furthermore, assume that  ,
,  , and
, and  is an eventually positive solution of (1.1). Then, there exists a
is an eventually positive solution of (1.1). Then, there exists a  such that
such that

Proof.
Suppose  is an eventually positive solution of (1.1) such that
is an eventually positive solution of (1.1) such that  and
and  for all
for all  . In view of (1.1), we have
. In view of (1.1), we have

and so  is an eventually decreasing function. We first show that
is an eventually decreasing function. We first show that  is eventually positive. Indeed, the decreasing function
is eventually positive. Indeed, the decreasing function  is either eventually positive or eventually negative. Suppose that there exists an integer
is either eventually positive or eventually negative. Suppose that there exists an integer  such that
such that  , then from (3.4) we have
, then from (3.4) we have  for
for  , hence
, hence

which implies by (1.8) that

and this contradicts the fact that  for all
for all  . Hence
. Hence  is eventually positive. So
is eventually positive. So  is eventually positive. Then
is eventually positive. Then  is eventually increasing.
is eventually increasing.
By (2.5), we get

From (3.4), (3.7), and  , we can easily verify that
, we can easily verify that  is eventually negative. Therefore, we see that there is some
is eventually negative. Therefore, we see that there is some  such that (3.3) holds. The proof is complete.
such that (3.3) holds. The proof is complete.
Lemma 3.3.
Let  and
and  be differentiable on time scale
be differentiable on time scale  with
with  for all
for all  . Then we have
. Then we have

The proof is similar to that of Akin-Bohner et al. [7, Lemma  ].
].
Theorem 3.4.
Assume that (1.8) holds,  , and
, and  ,
,  . Define
. Define

If

then (1.1) is oscillatory on  .
.
Proof.
Suppose that (1.1) has a nonoscillatory solution  . We may assume without loss of generality that
. We may assume without loss of generality that  and
and  for all
for all  . So by Lemma 3.2, (3.3) holds. Define the function
. So by Lemma 3.2, (3.3) holds. Define the function  by
by

Then,  and using (2.5) we get
and using (2.5) we get

By Lemma 3.1, for each  , there exists a constant
, there exists a constant  , such that
, such that

note that  , (3.1) and (3.3) imply
, (3.1) and (3.3) imply

So,

Upon integration, we arrive at

which contradicts (4.3). The proof is complete.
Remark 3.5.
Theorem 3.4 includes results of Akin-Bohner et al. [7, Theorem  ].
].
Putting  that is,
that is,  in Theorem 3.4, we obtain the following corollary.
in Theorem 3.4, we obtain the following corollary.
Corollary 3.6.
Assume  ,
,  . If
. If

then (1.1) is oscillatory on  .
.
Theorem 3.7.
Assume that (1.8) holds,  , and
, and  ,
,  . Furthermore, assume that there exists a function
. Furthermore, assume that there exists a function  such that
such that

holds for all constants  . Then (1.1) is oscillatory on
. Then (1.1) is oscillatory on  .
.
Proof.
Suppose that (1.1) has a nonoscillatory solution  . We may assume without loss of generality that
. We may assume without loss of generality that  and
and  for all
for all  . So by Lemma 3.2, (3.3) holds. Define the function
. So by Lemma 3.2, (3.3) holds. Define the function  by
by

Then, using (2.5) we get

So, from (1.1) and Lemma 3.3, we have

By Lemma 3.1, for each  , there exists a constant
, there exists a constant  , such that
, such that

note that  (3.1) and (3.3) imply
(3.1) and (3.3) imply

then

where  if
if  . If
. If  , we chose
, we chose  .
.
Therefore,

which contradicts (3.18). The proof is complete.
Remark 3.8.
Theorem 3.7 not only includes results of Agarwal et al. [14, Theorem  ], Akin-Bohner et al. [7, Theorem
], Akin-Bohner et al. [7, Theorem  ], and Han et al. [17, Theorem
], and Han et al. [17, Theorem  ], but also improves conditions of Agarwal et al. [14, Theorem
], but also improves conditions of Agarwal et al. [14, Theorem  ] and Han et al. [17, Theorem
] and Han et al. [17, Theorem  ].
].
From Theorem 3.7, we can obtain different conditions for oscillation of all solutions of (1.1) with different choices of  .
.
For example, let  . Now Theorem 3.4 yields the following results.
. Now Theorem 3.4 yields the following results.
Corollary 3.9.
Assume that (1.8) holds,  , and
, and  ,
,  . If
. If

holds for all constants  , then (1.1) is oscillatory on
, then (1.1) is oscillatory on  .
.
Sometimes the following criterion is easier to check than the one given in Corollary 3.6, but it follows easily from Corollary 3.6 as we always have  for all
for all  .
.
Corollary 3.10.
Assume that (1.8) holds,  , and
, and  ,
,  . If
. If

holds for all constants  , then (1.1) is oscillatory on
, then (1.1) is oscillatory on  .
.
Now, using Lemma 3.2, we can give some sufficient conditions when (1.9) holds, which guarantee that every solution of (1.1) oscillates or converges to zero in  .
.
Theorem 3.11.
Assume that (1.9) holds,  , and
, and  , and
, and  . Furthermore, assume that there exists a positive function
. Furthermore, assume that there exists a positive function  such that (3.18) holds. If
such that (3.18) holds. If

then every solution of (1.1) is oscillatory or converges to zero on  .
.
Theorem 3.12.
Assume that (1.8) holds,  , and
, and  ,
,  . Furthermore, assume that there exists a function
. Furthermore, assume that there exists a function  such that
such that

holds for all constants  . Then (1.1) is oscillatory on
. Then (1.1) is oscillatory on  .
.
Proof.
We assume that (1.1) has a nonoscillatory solution such that  and
and  , for all
, for all  . By Lemma 3.2, we obtain (3.3). We calculate
. By Lemma 3.2, we obtain (3.3). We calculate

where  and
and  . By putting
. By putting  and
and  , we find that
, we find that

Now note that  , (3.1) and (3.31) imply
, (3.1) and (3.31) imply

So,

where we put  if
if  . If
. If  , we chose
, we chose  . Note
. Note  . Now define the function
. Now define the function  by (3.19). Therefore, using (3.21), Lemma 3.1, for each
by (3.19). Therefore, using (3.21), Lemma 3.1, for each  , there exists a constant
, there exists a constant  , such that
, such that

noting that (3.3) and (3.33), we obtain
(3.3) and (3.33), we obtain

where  if
if  . If
. If  , we chose
, we chose  . Upon integration, we arrive at
. Upon integration, we arrive at

which contradicts (3.29). The proof is complete.
Remark 3.13.
Theorem 3.12 includes results of Akin-Bohner et al. [7, Theorem  ] and Han et al. [17, Theorem
] and Han et al. [17, Theorem  ] and improves conditions of Han [17, Theorem
] and improves conditions of Han [17, Theorem  ].
].
From Theorem 3.12, we can obtain different conditions for oscillation of all solutions of (1.1) with different choices of  .
.
For example, let  . Now Theorem 3.12 yields the following results.
. Now Theorem 3.12 yields the following results.
Corollary 3.14.
Assume that (1.8) holds,  , and
, and  ,
,  . If
. If

holds for all constants  , then (1.1) is oscillatory on
, then (1.1) is oscillatory on  .
.
Sometimes the following criterion is easier to check than the one given in Corollary 3.14, but it follows easily from Corollary 3.14 as we always have  for all
for all  .
.
Corollary 3.15.
Assume that (1.8) holds,  , and
, and  ,
,  . If
. If

holds for all constants  , then (1.1) is oscillatory on
, then (1.1) is oscillatory on  .
.
4. Applications
In this section, we give one example to illustrate our main results. To obtain the conditions for oscillation, we will use the following fact:

For more details, we refer the reader to [4, Theorem  ].
].
Akin-Bohner et al. [7] considered the second-order dynamic equations on time scales

where  is a quotient of odd positive integer,
is a quotient of odd positive integer,  and
and  are positive, real-valued rd-continuous functions defined on
are positive, real-valued rd-continuous functions defined on  , and established some new oscillation criteria of (4.2).
, and established some new oscillation criteria of (4.2).
Theorem 4.1 (Akin-Bohner et al. [7, Theorem  ]).
]).
Assume that (1.8) holds. If

then (4.2) is oscillatory on  .
.
We note that (1.1) becomes (4.2) when  , and Theorem 3.4 becomes Theorem 4.1, so Theorem 3.4 essentially includes results of Akin-Bohner et al. [7, Theorem
, and Theorem 3.4 becomes Theorem 4.1, so Theorem 3.4 essentially includes results of Akin-Bohner et al. [7, Theorem  ].
].
Example 4.2.
Consider the second-order delay dynamic equations on time scales

where  . By Corollary 3.10, we have
. By Corollary 3.10, we have

Let  , then
, then  , pick
, pick  , so
, so  for all
for all  . Therefore,
. Therefore,

for all constants  . Then (4.4) is oscillatory on
. Then (4.4) is oscillatory on  .
.
References
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Agarwal RP, Bohner M, O'Regan D, Peterson A: Dynamic equations on time scales: a survey. Journal of Computational and Applied Mathematics 2002,141(1-2):1-26. 10.1016/S0377-0427(01)00432-0
Bohner M, Peterson A: Dynamic Equations on Time Scales. An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Akin-Bohner E, Hoffacker J: Oscillation properties of an Emden-Fowler type equation on discrete time scales. Journal of Difference Equations and Applications 2003,9(6):603-612. 10.1080/1023619021000053575
Akin-Bohner E, Hoffacker J: Solution properties on discrete time scales. Journal of Difference Equations and Applications 2003,9(1):63-75.
Akin-Bohner E, Bohner M, Saker SH: Oscillation criteria for a certain class of second order Emden-Fowler dynamic equations. Electronic Transactions on Numerical Analysis 2007, 27: 1-12.
Bohner M, Saker SH: Oscillation of second order nonlinear dynamic equations on time scales. The Rocky Mountain Journal of Mathematics 2004,34(4):1239-1254. 10.1216/rmjm/1181069797
Erbe L: Oscillation results for second-order linear equations on a time scale. Journal of Difference Equations and Applications 2002,8(11):1061-1071. 10.1080/10236190290015317
Erbe L, Peterson A, Saker SH: Oscillation criteria for second-order nonlinear dynamic equations on time scales. Journal of the London Mathematical Society 2003,67(3):701-714. 10.1112/S0024610703004228
Li T, Han Z, Sun S, Zhang C: Forced oscillation of second-order nonlinear dynamic equations on time scales. Electronic Journal of Qualitative Theory of Differential Equations 2009, 60: 1-8.
Saker SH: Oscillation criteria of second-order half-linear dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,177(2):375-387. 10.1016/j.cam.2004.09.028
Saker SH: Oscillation of nonlinear dynamic equations on time scales. Applied Mathematics and Computation 2004,148(1):81-91. 10.1016/S0096-3003(02)00829-9
Agarwal RP, Bohner M, Saker SH: Oscillation of second order delay dynamic equations. The Canadian Applied Mathematics Quarterly 2005,13(1):1-17.
Agarwal RP, O'Regan D, Saker SH: Oscillation criteria for second-order nonlinear neutral delay dynamic equations. Journal of Mathematical Analysis and Applications 2004,300(1):203-217. 10.1016/j.jmaa.2004.06.041
Bohner M: Some oscillation criteria for first order delay dynamic equations. Far East Journal of Applied Mathematics 2005,18(3):289-304.
Han Z, Sun S, Shi B: Oscillation criteria for a class of second-order Emden-Fowler delay dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2007,334(2):847-858. 10.1016/j.jmaa.2007.01.004
Han Z, Shi B, Sun S: Oscillation criteria for second-order delay dynamic equations on time scales. Advances in Difference Equations 2007, 2007:-16.
Han ZL, Shi B, Sun SR: Oscillation of second-order delay dynamic equations on time scales. Acta Scientiarum Naturalium Universitatis Sunyatseni 2007,46(6):10-13.
Han Z, Li T, Sun S, Zhang C: Oscillation for second-order nonlinear delay dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-13.
Han Z, Li T, Sun S, Zhang C: Oscillation behavior of third order neutral Emden-Fowler delay dynamic equations on time scales. Advances in Difference Equations 2010, 2010:-23.
Li T, Han Z, Sun S, Yang D: Existence of nonoscillatory solutions to second-order neutral delay dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-10.
Şahiner Y: Oscillation of second-order delay differential equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2005,63(5–7):e1073-e1080.
Saker SH: Oscillation of second-order nonlinear neutral delay dynamic equations on time scales. Journal of Computational and Applied Mathematics 2006,187(2):123-141. 10.1016/j.cam.2005.03.039
Sun S-R, Han Z-L, Zhang C-H: Oscillation criteria of second-order Emden-Fowler neutral delay dynamic equations on time scales. Journal of Shanghai Jiaotong University 2008,42(12):2070-2075.
Sun S, Han Z, Zhang C: Oscillation of second-order delay dynamic equations on time scales. Journal of Applied Mathematics and Computing 2009,30(1-2):459-468. 10.1007/s12190-008-0185-6
Sun Y, Han Z, Li T, Zhang G: Oscillation criteria for second-order quasilinear neutral delay dynamic equations on time scales. Advances in Difference Equations 2010, 2010:-14.
Erbe L, Peterson A, Saker SH: Oscillation criteria for second-order nonlinear delay dynamic equations. Journal of Mathematical Analysis and Applications 2007,333(1):505-522. 10.1016/j.jmaa.2006.10.055
Zhang BG, Shanliang Z: Oscillation of second-order nonlinear delay dynamic equations on time scales. Computers & Mathematics with Applications 2005,49(4):599-609. 10.1016/j.camwa.2004.04.038
Erbe L: Oscillation criteria for second order nonlinear delay equations. Canadian Mathematical Bulletin 1973,67(16):49-56. 10.4153/CMB-1973-011-1
Agarwal RP, Shieh S-L, Yeh C-C: Oscillation criteria for second-order retarded differential equations. Mathematical and Computer Modelling 1997,26(4):1-11. 10.1016/S0895-7177(97)00141-6
Chen SZ, Erbe LH: Riccati techniques and discrete oscillations. Journal of Mathematical Analysis and Applications 1989,142(2):468-487. 10.1016/0022-247X(89)90015-2
Chen SZ, Erbe LH: Oscillation and nonoscillation for systems of selfadjoint second-order difference equations. SIAM Journal on Mathematical Analysis 1989,20(4):939-949. 10.1137/0520063
Ohriska J: Oscillation of second order delay and ordinary differential equation. Czechoslovak Mathematical Journal 1984,34(109)(1):107-112.
Thandapani E, Ravi K, Graef JR: Oscillation and comparison theorems for half-linear second-order difference equations. Computers & Mathematics with Applications 2001,42(6-7):953-960. 10.1016/S0898-1221(01)00211-5
Zhang Z, Chen J, Zhang C: Oscillation of solutions for second-order nonlinear difference equations with nonlinear neutral term. Computers & Mathematics with Applications 2001,41(12):1487-1494. 10.1016/S0898-1221(01)00113-4
Acknowledgments
This research is supported by the Natural Science Foundation of China (60774004, 60904024), China Postdoctoral Science Foundation funded project (20080441126, 200902564), Shandong Postdoctoral funded project (200802018), and supported by the Natural Science Foundation of Shandong (Y2008A28, ZR2009AL003), also supported by the Fund of Doctoral Program Research of University of Jinan (B0621, XBS0843).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, S., Han, Z., Zhao, P. et al. Oscillation for a Class of Second-Order Emden-Fowler Delay Dynamic Equations on Time Scales. Adv Differ Equ 2010, 642356 (2010). https://doi.org/10.1155/2010/642356
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/642356
 , where
, where  for some
for some  ;
;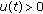 ,
,  and
and 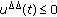 for
for  .
.