- Research Article
- Open access
- Published:
Transformations of Difference Equations II
Advances in Difference Equations volume 2010, Article number: 623508 (2010)
Abstract
This is an extension of the work done by Currie and Love (2010) where we studied the effect of applying two Crum-type transformations to a weighted second-order difference equation with non-eigenparameter-dependent boundary conditions at the end points. In particular, we now consider boundary conditions which depend affinely on the eigenparameter together with various combinations of Dirichlet and non-Dirichlet boundary conditions. The spectra of the resulting transformed boundary value problems are then compared to the spectra of the original boundary value problems.
1. Introduction
This paper continues the work done in [1], where we considered a weighted second-order difference equation of the following form:

with  representing a weight function and
representing a weight function and  a potential function.
a potential function.
This paper is structured as follows.
The relevant results from [1], which will be used throughout the remainder of this paper, are briefly recapped in Section 2.
In Section 3, we show how non-Dirichlet boundary conditions transform to affine  -dependent boundary conditions. In addition, we provide conditions which ensure that the linear function (in
-dependent boundary conditions. In addition, we provide conditions which ensure that the linear function (in  ) in the affine
) in the affine  -dependent boundary conditions is a Nevanlinna or Herglotz function.
-dependent boundary conditions is a Nevanlinna or Herglotz function.
Section 4 gives a comparison of the spectra of all possible combinations of Dirichlet and non-Dirichlet boundary value problems with their transformed counterparts. It is shown that transforming the boundary value problem given by (2.2) with any one of the four combinations of Dirichlet and non-Dirichlet boundary conditions at the end points using (3.1) results in a boundary value problem with one extra eigenvalue in each case. This is done by considering the degree of the characteristic polynomial for each boundary value problem.
It is shown, in Section 5, that we can transform affine  -dependent boundary conditions back to non-Dirichlet type boundary conditions. In particular, we can transform back to the original boundary value problem.
-dependent boundary conditions back to non-Dirichlet type boundary conditions. In particular, we can transform back to the original boundary value problem.
To conclude, we outline briefly how the process given in the sections above can be reversed.
2. Preliminaries
Consider the second-order difference equation (1.1) for  with boundary conditions
with boundary conditions

where  and
and  are constants, see [2]. Without loss of generality, by a shift of the spectrum, we may assume that the least eigenvalue,
are constants, see [2]. Without loss of generality, by a shift of the spectrum, we may assume that the least eigenvalue,  , of (1.1), (2.1) is
, of (1.1), (2.1) is  .
.
We recall the following important results from [1]. The mapping  defined for
defined for  by
by  , where
, where  is the eigenfunction of (1.1), (2.1) corresponding to the eigenvalue
is the eigenfunction of (1.1), (2.1) corresponding to the eigenvalue  , produces the following transformed equation:
, produces the following transformed equation:

where

Moreover,  obeying the boundary conditions (2.1) transforms to
obeying the boundary conditions (2.1) transforms to  obeying the Dirichlet boundary conditions as follows:
obeying the Dirichlet boundary conditions as follows:

Applying the mapping  given by
given by  for
for  , where
, where  is a solution of (2.2) with
is a solution of (2.2) with  , where
, where  is less than the least eigenvalue of (2.2), (2.4), such that
is less than the least eigenvalue of (2.2), (2.4), such that  for all
for all  , results in the following transformed equation:
, results in the following transformed equation:

where, for  ,
,

Here, we take  , thus
, thus  is defined for
is defined for  .
.
In addition,  obeying the Dirichlet boundary conditions (2.4) transforms to
obeying the Dirichlet boundary conditions (2.4) transforms to  obeying the non-Dirichlet boundary conditions as follows:
obeying the non-Dirichlet boundary conditions as follows:

where

3. Non-Dirichlet to Affine
In this section, we show how  obeying the non-Dirichlet boundary conditions (3.2), (3.13) transforms under the following mapping:
obeying the non-Dirichlet boundary conditions (3.2), (3.13) transforms under the following mapping:

to give  obeying boundary conditions which depend affinely on the eigenparamter
obeying boundary conditions which depend affinely on the eigenparamter  . We provide constraints which ensure that the form of these affine
. We provide constraints which ensure that the form of these affine  -dependent boundary conditions is a Nevanlinna/Herglotz function.
-dependent boundary conditions is a Nevanlinna/Herglotz function.
Theorem 3.1.
Under the transformation (3.1),  obeying the boundary conditions
obeying the boundary conditions

for  , transforms to
, transforms to  obeying the boundary conditions
obeying the boundary conditions

where  ,
,  and
and  . Here,
. Here,  and
and  is a solution of (2.2) for
is a solution of (2.2) for  , where
, where  is less than the least eigenvalue of (2.2), (3.2), and (3.13) such that
is less than the least eigenvalue of (2.2), (3.2), and (3.13) such that  for
for  .
.
Proof.
The values of  for which
for which  exists are
exists are  . So to impose a boundary condition at
. So to impose a boundary condition at  , we need to extend the domain of
, we need to extend the domain of  to include
to include  . We do this by forcing the boundary condition (3.3) and must now show that the equation is satisfied on the extended domain.
. We do this by forcing the boundary condition (3.3) and must now show that the equation is satisfied on the extended domain.
Evaluating (2.5) at  for
for  and using (3.3) gives the following:
and using (3.3) gives the following:

Also from (3.1) for  and
and  , we obtain the following:
, we obtain the following:

Substituting (3.2) into the above equation yields

Thus, (3.4) becomes

This may be slightly rewritten as follows

Also from (2.2), with  , together with (3.2), we have the following:
, together with (3.2), we have the following:

Subtracting (3.9) from (3.8) and using the fact that  results in
results in

Equating coefficients of  on both sides gives the following:
on both sides gives the following:

and equating coefficients of  on both sides gives the following:
on both sides gives the following:

where  , and recall
, and recall  .
.
Note that for  , this corresponds to the results in [1] for
, this corresponds to the results in [1] for  .
.
Theorem 3.2.
Under the transformation (3.1),  satisfying the boundary conditions
satisfying the boundary conditions

for  , transforms to
, transforms to  obeying the boundary conditions
obeying the boundary conditions

where  ,
,  , and
, and  . Here,
. Here,  is a solution to (2.2) for
is a solution to (2.2) for  , where
, where  is less than the least eigenvalue of (2.2), (3.2), and (3.13) such that
is less than the least eigenvalue of (2.2), (3.2), and (3.13) such that  in the given interval,
in the given interval,  .
.
Proof.
Evaluating (3.1) at  and
and  gives the following:
gives the following:


By considering  satisfying (2.2) at
satisfying (2.2) at  , we obtain that
, we obtain that

Substituting (3.17) into (3.16) gives the following:

Now using (3.13) together with (3.15) yields

which in turn, by substituting into (3.13), gives the following:

Thus, by putting (3.19) and (3.20) into (3.18), we obtain

The equation above may be rewritten as follows:

Now, since  is a solution to (2.2) for
is a solution to (2.2) for  , we have that
, we have that

Substituting (3.23) into (3.22) gives the following:

Setting  yields
yields

Hence,

which is of the form (3.14), where  ,
,  , and
, and  .
.
Note that if we require that  in (3.3) be a Nevanlinna or Herglotz function, then we must have that
in (3.3) be a Nevanlinna or Herglotz function, then we must have that  . This condition provides constraints on the allowable values of
. This condition provides constraints on the allowable values of  .
.
Remark 3.3.
In Theorems 3.1 and 3.2, we have taken  to be a solution of (2.2) for
to be a solution of (2.2) for  with
with  less than the least eigenvalue of (2.2), (3.2), and (3.13) such that
less than the least eigenvalue of (2.2), (3.2), and (3.13) such that  in
in  . We assume that
. We assume that  does not obey the boundary conditions (3.2) and (3.13) which is sufficient for the results which we wish to obtain in this paper. However, this case will be dealt with in detail in a subsequent paper.
does not obey the boundary conditions (3.2) and (3.13) which is sufficient for the results which we wish to obtain in this paper. However, this case will be dealt with in detail in a subsequent paper.
Theorem 3.4.
If  where
where  is a solution to (2.2) for
is a solution to (2.2) for  with
with  less than the least eigenvalue of (2.2), (3.2), and (3.13) and
less than the least eigenvalue of (2.2), (3.2), and (3.13) and  in the given interval
in the given interval  , then the values of
, then the values of  which ensure that
which ensure that  in (3.3), that is, which ensure that
in (3.3), that is, which ensure that  in (3.3) is a Nevanlinna function are
in (3.3) is a Nevanlinna function are

Proof.
From Theorem 3.1, we have that

Assume that  , then to ensure that
, then to ensure that  we require that either
we require that either  and
and  or
or  and
and  . For the first case, since
. For the first case, since  , we get
, we get  and
and  . For the second case, we obtain
. For the second case, we obtain  and
and  , which is not possible. Thus, allowable values of
, which is not possible. Thus, allowable values of  for
for  are
are

Since  If
If  , then we must have that either
, then we must have that either  and
and  or
or  and
and  . The first case of
. The first case of  is not possible since
is not possible since  and
and  ,
,  , which implies that
, which implies that  in particular for
in particular for  . For the second case, we get
. For the second case, we get  and
and  which is not possible. Thus for
which is not possible. Thus for  , there are no allowable values of
, there are no allowable values of  .
.
Also, if we require that  from (3.14) be a Nevanlinna/Herglotz function, then we must have
from (3.14) be a Nevanlinna/Herglotz function, then we must have  . This provides conditions on the allowable values of
. This provides conditions on the allowable values of  .
.
Corollary 3.5.
If  where
where  is a solution to (2.2) for
is a solution to (2.2) for  with
with  less than the least eigenvalue of (2.2), (3.2), and (3.13), and
less than the least eigenvalue of (2.2), (3.2), and (3.13), and  in the given interval
in the given interval  , then
, then

Proof.
Without loss of generality, we may shift the spectrum of (2.2) with boundary conditions (3.2), (3.13), such that the least eigenvalue of (2.2) with boundary conditions (3.2), (3.13) is strictly greater than  , and thus we may assume that
, and thus we may assume that  .
.
Since  , we consider the two cases,
, we consider the two cases,  and
and  .
.
Assume that  , then the numerator of
, then the numerator of  is strictly positive. Thus, to ensure that
is strictly positive. Thus, to ensure that  the denominator must be strictly positive, that is,
the denominator must be strictly positive, that is,  . So either
. So either  and
and  or
or  and
and  . Since
. Since  , we have that either
, we have that either  and
and  or
or  and
and  . Thus, if
. Thus, if  , that is,
, that is,  , we get
, we get

and if  , that is,
, that is,  , we get
, we get

Now if  , then the numerator of
, then the numerator of  is strictly negative. Thus, in order that
is strictly negative. Thus, in order that  , we require that the denominator is strictly negative, that is,
, we require that the denominator is strictly negative, that is,  . So either
. So either  and
and  or
or  and
and  . As
. As  , we obtain that either
, we obtain that either  and
and  or
or  and
and  . These are the same conditions as we had on
. These are the same conditions as we had on  for
for  . Thus, the sign of
. Thus, the sign of  does not play a role in finding the allowable values of
does not play a role in finding the allowable values of  which ensure that
which ensure that  , and hence we have the required result.
, and hence we have the required result.
4. Comparison of the Spectra
In this section, we see how the transformation, (3.1), affects the spectrum of the difference equation with various boundary conditions imposed at the initial and terminal points.
By combining the results of [1, conclusion] with Theorems 3.1 and 3.2, we have proved the following result.
Theorem 4.1.
Assume that  satisfies (2.2). Consider the following four sets of boundary conditions:
satisfies (2.2). Consider the following four sets of boundary conditions:




The transformation (3.1), where  is a solution to (2.2) for
is a solution to (2.2) for  , where
, where  is less than the least eigenvalue of (2.2) with one of the four sets of boundary conditions above, such that
is less than the least eigenvalue of (2.2) with one of the four sets of boundary conditions above, such that  in the given interval
in the given interval  , takes
, takes  obeying (2.2) to
obeying (2.2) to  obeying (2.5).
obeying (2.5).
In addition,
-
(i)
 obeying (4.1) transforms to
obeying (4.1) transforms to 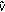 obeying
obeying (4.5)
(4.5)where
 and
and (4.6)
(4.6)where
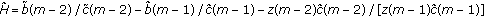 with
with 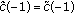 .
. -
(ii)
 obeying (4.2) transforms to
obeying (4.2) transforms to 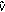 obeying (4.5) and (3.14).
obeying (4.5) and (3.14). -
(iii)
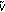 obeying(4.3) transforms to
obeying(4.3) transforms to  obeying (3.3) and (4.6).
obeying (3.3) and (4.6). -
(iv)
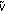 obeying (4.4) transforms to
obeying (4.4) transforms to  obeying (3.3) and (3.14).
obeying (3.3) and (3.14).
The next theorem, shows that the boundary value problem given by  obeying (2.2) together with any one of the four types of boundary conditions in the above theorem has
obeying (2.2) together with any one of the four types of boundary conditions in the above theorem has  eigenvalues as a result of the eigencondition being the solution of an
eigenvalues as a result of the eigencondition being the solution of an  th order polynomial in
th order polynomial in  . It should be noted that if the boundary value problem considered is self-adjoint, then the eigenvalues are real, otherwise the complex eigenvalues will occur as conjugate pairs.
. It should be noted that if the boundary value problem considered is self-adjoint, then the eigenvalues are real, otherwise the complex eigenvalues will occur as conjugate pairs.
Theorem 4.2.
The boundary value problem given by  obeying (2.2) together with any one of the four types of boundary conditions given by (4.1) to (4.4) has
obeying (2.2) together with any one of the four types of boundary conditions given by (4.1) to (4.4) has  eigenvalues.
eigenvalues.
Proof.
Since  obeys (2.2), we have that, for
obeys (2.2), we have that, for  ,
,

So setting  , in (4.7), gives the following:
, in (4.7), gives the following:

For the boundary conditions (4.1) and (4.2), we have that  giving
giving

where  and
and  are real constants, that is, a first order polynomial in
are real constants, that is, a first order polynomial in  .
.
Also  in (4.7) gives that
in (4.7) gives that

Substituting in for  , from above, we obtain
, from above, we obtain

where again  are real constants, that is, a quadratic polynomial in
are real constants, that is, a quadratic polynomial in  .
.
Thus, by an easy induction, we have that

where  ,
,  and
and  ,
,  are real constants, that is, an
are real constants, that is, an  th and an
th and an  th order polynomial in
th order polynomial in  , respectively.
, respectively.
Now, (4.1) gives  , that is,
, that is,

So our eigencondition is given by

which is an  th order polynomial in
th order polynomial in  and, therefore, has
and, therefore, has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.2) with (4.1) has
obeying (2.2) with (4.1) has  eigenvalues.
eigenvalues.
Next, (4.2) gives  , so
, so

from which we obtain the following eigencondition:

This is again an  th order polynomial in
th order polynomial in  and therefore has
and therefore has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.2) with (4.2) has
obeying (2.2) with (4.2) has  eigenvalues.
eigenvalues.
Now for the boundary conditions (4.3) and (4.4), we have that  , thus (4.8) becomes
, thus (4.8) becomes

where  and
and  are real constants, that is, a first order polynomial in
are real constants, that is, a first order polynomial in  .
.
Using  and
and  from above, we can show that
from above, we can show that  can be written as the following:
can be written as the following:

where again  ,
,  are real constants, that is, a quadratic polynomial in
are real constants, that is, a quadratic polynomial in  .
.
Thus, by induction,

where  ,
,  and
and  ,
,  are real constants, thereby giving an
are real constants, thereby giving an  th and an
th and an  th order polynomial in
th order polynomial in  , respectively.
, respectively.
Now, (4.3) gives  , that is,
, that is,

So our eigencondition is given by

which is an  th order polynomial in
th order polynomial in  and, therefore, has
and, therefore, has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.2) with (4.3) has
obeying (2.2) with (4.3) has  eigenvalues.
eigenvalues.
Lastly, (4.4) gives  , that is,
, that is,

from which we obtain the following eigencondition:

This is again an  th order polynomial in
th order polynomial in  and therefore has
and therefore has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.2) with (4.4) has
obeying (2.2) with (4.4) has  eigenvalues.
eigenvalues.
In a similar manner, we now prove that the transformed boundary value problems given in Theorem 4.1 have  eigenvalues, that is, the spectrum increases by one in each case.
eigenvalues, that is, the spectrum increases by one in each case.
Theorem 4.3.
The boundary value problem given by  obeying (2.5),
obeying (2.5),  , together with any one of the four types of transformed boundary conditions given in (i) to (iv) in Theorem 4.1 has
, together with any one of the four types of transformed boundary conditions given in (i) to (iv) in Theorem 4.1 has  eigenvalues. The additional eigenvalue is precisely
eigenvalues. The additional eigenvalue is precisely  with corresponding eigenfunction
with corresponding eigenfunction  , as given in Theorem 4.1.
, as given in Theorem 4.1.
Proof.
The proof is along the same lines as that of Theorem 4.2. By Theorem 3.1, we have extended  , such that
, such that  exists for
exists for  .
.
Since  obeys (2.5), we have that, for
obeys (2.5), we have that, for  ,
,

For the transformed boundary conditions in (i) and (ii) of Theorem 4.1, we have that (4.5) is obeyed, and as in Theorem 4.2, we can inductively show that

and also by [1], we can extend the domain of  to include
to include  if necessary by forcing (4.6) and then
if necessary by forcing (4.6) and then

where  ,
,  ,
,  ,
,  , and
, and  ,
,  are real constants, that is, an
are real constants, that is, an  th,
th,  th, and
th, and  th order polynomial in
th order polynomial in  , respectively.
, respectively.
Now for (i), the boundary condition (4.6) gives the following:

Therefore, the eigencondition is

which is an  th order polynomial in
th order polynomial in  and thus has
and thus has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.5) with transformed boundary conditions (i), that is, (4.5) and (4.6), has
obeying (2.5) with transformed boundary conditions (i), that is, (4.5) and (4.6), has  eigenvalues.
eigenvalues.
Also, for (ii), from the boundary condition (3.14), we get

Therefore, the eigencondition is

which is an  th order polynomial in
th order polynomial in  and thus has
and thus has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.5) with transformed boundary conditions (ii), that is, (4.5) and (3.14), has
obeying (2.5) with transformed boundary conditions (ii), that is, (4.5) and (3.14), has  eigenvalues.
eigenvalues.
Putting  in (4.24), we get
in (4.24), we get

For the boundary conditions in (iii) and (iv), we have that (3.3) is obeyed, thus,

where  ,
,  , and
, and  are real constants.
are real constants.
Putting  in (4.24), we get
in (4.24), we get

which, by using (3.3) and  , can be rewritten as follows:
, can be rewritten as follows:

where  ,
,  ,
,  ,
,  , and
, and  are real constants.
are real constants.
Thus, inductively we obtain

Also, by [1], we can again extend the domain of  to include
to include  , if needed, by forcing (4.6), thus,
, if needed, by forcing (4.6), thus,

where all the coefficients of  are real constants.
are real constants.
The transformed boundary conditions (iii) mean that (4.6) is obeyed, thus, our eigencondition is

which is an  th order polynomial in
th order polynomial in  and thus has
and thus has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.5) with transformed boundary conditions (iii), that is, (3.3) and (4.6), has
obeying (2.5) with transformed boundary conditions (iii), that is, (3.3) and (4.6), has  eigenvalues.
eigenvalues.
Also, the transformed boundary conditions in (iv) give (3.14) which produces the following eigencondition:

which is an  th order polynomial in
th order polynomial in  and thus has
and thus has  roots. Hence, the boundary value problem given by
roots. Hence, the boundary value problem given by  obeying (2.5) with transformed boundary conditions (iv), that is, (3.3) and (3.14), has
obeying (2.5) with transformed boundary conditions (iv), that is, (3.3) and (3.14), has  eigenvalues.
eigenvalues.
Lastly, we have that (3.1) transforms eigenfunctions of any of the boundary value problems in Theorem 4.2 to eigenfunctions of the corresponding transformed boundary value problem, see Theorem 4.2. In particular, if  are the eigenvalues of the original boundary value problem with corresponding eigenfunctions
are the eigenvalues of the original boundary value problem with corresponding eigenfunctions  , then
, then  are eigenfunctions of the corresponding transformed boundary value problem with eigenvalues
are eigenfunctions of the corresponding transformed boundary value problem with eigenvalues  . Since we know that the transformed boundary value problem has
. Since we know that the transformed boundary value problem has  eigenvalues, it follows that
eigenvalues, it follows that  constitute all the eigenvalues of the transformed boundary value problem, see [1].
constitute all the eigenvalues of the transformed boundary value problem, see [1].
5. Affine to Non-Dirichlet
In this section, we now show that the process in Section 3 may be reversed. In particular, by applying the following mapping:

we can transform  obeying affine
obeying affine  -dependent boundary conditions to
-dependent boundary conditions to  obeying non-Dirichlet boundary conditions.
obeying non-Dirichlet boundary conditions.
Theorem 5.1.
Consider the boundary value problem given by  satisfying (2.5) with the following boundary conditions:
satisfying (2.5) with the following boundary conditions:


The transformation (5.1), for  , where
, where  is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue
is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue  , yields the following equation:
, yields the following equation:

where, for  ,
,

In addition,  obeying (5.2) and (5.3) transforms to
obeying (5.2) and (5.3) transforms to  obeying the non-Dirichlet boundary conditions
obeying the non-Dirichlet boundary conditions


where  and
and  .
.
Proof.
The fact that  , obeying (2.5), transforms to
, obeying (2.5), transforms to  , obeying (5.4), was covered in [1, conclusion]. Now,
, obeying (5.4), was covered in [1, conclusion]. Now,  is defined for
is defined for  and is extended to
and is extended to  by (5.2). Thus,
by (5.2). Thus,  is defined for
is defined for  giving that (5.4) is valid for
giving that (5.4) is valid for  . For
. For  and
and  , (5.1) gives the following:
, (5.1) gives the following:


Setting  in (2.5) gives the following:
in (2.5) gives the following:

which by using (5.2) becomes

Since  is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue
is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue  , we have that
, we have that

and hence

Substituting (5.11) and (5.13) into (5.8) and using (5.2), we obtain

Since  , everything can be written over the common denominator
, everything can be written over the common denominator  . Taking out
. Taking out  and simplifying, we get
and simplifying, we get

Thus,

Substituting (5.2) into (5.9) gives the following:

Hence, by putting (5.16) into (5.17), we get

So to impose the boundary condition (5.7), it is necessary to extend the domain of  by forcing the boundary condition (5.7). We must then check that
by forcing the boundary condition (5.7). We must then check that  satisfies the equation on the extended domain.
satisfies the equation on the extended domain.
Evaluating (5.4) at  and using (5.7) give the following:
and using (5.7) give the following:

Using (5.1) with  and
and  together with (5.3), we obtain
together with (5.3), we obtain

Substituting the above two equations into (5.19) yields

Since  is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue
is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue  we have that
we have that  . Thus, the above equation can be simplified to
. Thus, the above equation can be simplified to

Also (2.5) evaluated at  for
for  together with (5.3) gives
together with (5.3) gives

Adding (5.22) to (5.23) and using the fact that  yields
yields

By substituting in for  and
and  , it is easy to see that all the
, it is easy to see that all the  terms cancel out. Next, we examine the coefficients of
terms cancel out. Next, we examine the coefficients of  , and using
, and using  , we obtain that the coefficient of
, we obtain that the coefficient of  is
is

which equals  by (2.5) evaluated at
by (2.5) evaluated at  . Thus, only the terms in
. Thus, only the terms in  remain. First, we note that by substituting in for
remain. First, we note that by substituting in for  ,
,  and
and  we get
we get

Thus, equating coefficients of  gives the following:
gives the following:

Since  , we can divide and solve for
, we can divide and solve for  to obtain
to obtain

Note that the case of  , that is, a non-Dirichlet boundary condition, gives
, that is, a non-Dirichlet boundary condition, gives  , that is,
, that is,  which corresponds to the results obtained in [1].
which corresponds to the results obtained in [1].
If we set  , with
, with  a solution of (2.2) for
a solution of (2.2) for  where
where  less than the least eigenvalue of (2.2), (3.2), and (3.13) and
less than the least eigenvalue of (2.2), (3.2), and (3.13) and  in the given interval
in the given interval  , then
, then  is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue
is an eigenfunction of (2.5), (5.2), and (5.3) corresponding to the eigenvalue  . To see that
. To see that  satisfies (2.5), see [1, Lemma
satisfies (2.5), see [1, Lemma  ] with, as previously,
] with, as previously,  , and now
, and now  . Then, by construction,
. Then, by construction,  obeys (5.2). We now show that
obeys (5.2). We now show that  obeys (5.3). Let
obeys (5.3). Let  ,
,

Now  is a solution of (2.2) for
is a solution of (2.2) for  , thus,
, thus,

Remark 5.2.
For  ,
,  ,
,  ,
,  , and
, and  as above, the transformation (5.1), in Theorem 5.1, results in the original given boundary value problem. In particular, we obtain that in Theorem 5.1
as above, the transformation (5.1), in Theorem 5.1, results in the original given boundary value problem. In particular, we obtain that in Theorem 5.1  and
and  , see [1, Theorem
, see [1, Theorem  .2]. In addition,
.2]. In addition,

That is, the boundary value problem given by  satisfying (2.5) with boundary conditions (5.2), (5.3) transforms under (5.1) to
satisfying (2.5) with boundary conditions (5.2), (5.3) transforms under (5.1) to  obeying (2.2) with boundary conditions (3.2), (3.13) which is the original boundary value problem.
obeying (2.2) with boundary conditions (3.2), (3.13) which is the original boundary value problem.
We now verify that  . Let
. Let

Since  , we obtain
, we obtain  , and thus
, and thus

Also,  . Dividing through by
. Dividing through by  and using
and using  together with
together with  gives the following:
gives the following:

Now,

and since  satisfies (2.2) at
satisfies (2.2) at  for
for  , we get
, we get

Thus, using (5.35) and (5.36), the numerator of  is simplified to
is simplified to

The denominator of  can be simplified using
can be simplified using  to
to

hence  .
.
Finally, substituting in for  , we obtain
, we obtain

Thus,  , that is,
, that is,  .
.
Next, we show that  . Recall that
. Recall that  and
and

Let

Note that

and since  satisfies (2.2) at
satisfies (2.2) at  for
for  , we get
, we get

We now substitute in for  and
and  into the equation for
into the equation for  and use (5.42) and (5.43) to obtain that
and use (5.42) and (5.43) to obtain that

that is,  .
.
To summarise, we have the following.
Consider  obeying (2.5) with one of the following 4 types of boundary conditions:
obeying (2.5) with one of the following 4 types of boundary conditions:
-
(a)
non-Dirichlet and non-Dirichlet, that is, (4.5) and (4.6);
-
(b)
non-Dirichlet and affine, that is, (4.5) and (3.14);
-
(c)
affine and non-Dirichlet, that is, (3.3) and (4.6);
-
(d)
affine and affine, that is, (3.3) and (3.14).
By Theorem 4.3, each of the above boundary value problems have  eigenvalues.
eigenvalues.
Now, the transformation (5.1), with  an eigenfunction of (2.5) with boundary conditions (a) ((b), (c), (d), resp.) corresponding to the eigenvalue
an eigenfunction of (2.5) with boundary conditions (a) ((b), (c), (d), resp.) corresponding to the eigenvalue  , transforms
, transforms  obeying (2.5) to
obeying (2.5) to  obeying (2.2) and transforms the boundary conditions as follows:
obeying (2.2) and transforms the boundary conditions as follows:
-
(1)
boundary conditions (a) transform to
 and
and  ;
; -
(2)
boundary conditions (b) transform to
 and (3.13);
and (3.13); -
(3)
boundary conditions (c) transform to (3.2) and
 ;
; -
(4)
boundary conditions (d) transform to (3.2) and (3.13).
By Theorem 4.2, we know that the above transformed boundary value problems in  each have
each have  eigenvalues. In particular, if
eigenvalues. In particular, if  are the eigenvalues of (2.5), (a) ((b), (c), (d), resp.) with eigenfunctions
are the eigenvalues of (2.5), (a) ((b), (c), (d), resp.) with eigenfunctions  , then
, then  and
and  are eigenfunctions of (2.2), (1) ((2), (3), (4), resp.) with eigenvalues
are eigenfunctions of (2.2), (1) ((2), (3), (4), resp.) with eigenvalues  . Since we know that these boundary value problems have
. Since we know that these boundary value problems have  eigenvalues, it follows that
eigenvalues, it follows that  constitute all the eigenvalues.
constitute all the eigenvalues.
6. Conclusion
To conclude, we outline (the details are left to the reader to verify) how the entire process could also be carried out the other way around. That is, we start with a second order difference equation of the usual form, given in the previous sections, together with boundary conditions of one of the following forms:
-
(i)
non-Dirichlet at the initial point and affine at the terminal point;
-
(ii)
affine at the initial point and non-Dirichlet at the terminal point;
-
(iii)
affine at the initial point and at the terminal point.
We can then transform the above boundary value problem (by extending the domain where necessary, as done previously) to an equation of the same type with, respectively, transformed boundary conditions as follows:
-
(A)
Dirichlet at the initial point and non-Dirichlet at the terminal point;
-
(B)
non-Dirichlet at the initial point and Dirichlet at the terminal point;
-
(C)
non-Dirichlet at the initial point and at the terminal point.
It is then possible to return to the original boundary value problem by applying a suitable transformation to the transformed boundary value problem above.
References
Currie S, Love A: Transformations of difference equations I. Advances in Difference Equations 2010, 2010:-22.
Atkinson FV: Discrete and Continuous Boundary Problems, Mathematics in Science and Engineering, vol. 8. Academic Press, New York, NY, USA; 1964:xiv+570.
Acknowledgments
The authors would like to thank Professor Bruce A. Watson for his useful input and suggestions. This work was supported by NRF Grant nos. TTK2007040500005 and FA2007041200006.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Currie, S., Love, A.D. Transformations of Difference Equations II. Adv Differ Equ 2010, 623508 (2010). https://doi.org/10.1155/2010/623508
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/623508
 obeying (4.1) transforms to
obeying (4.1) transforms to 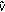 obeying
obeying
 and
and
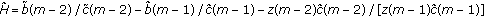 with
with 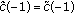 .
. obeying (4.2) transforms to
obeying (4.2) transforms to 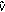 obeying (4.5) and (3.14).
obeying (4.5) and (3.14).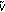 obeying(4.3) transforms to
obeying(4.3) transforms to  obeying (3.3) and (4.6).
obeying (3.3) and (4.6).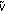 obeying (4.4) transforms to
obeying (4.4) transforms to  obeying (3.3) and (3.14).
obeying (3.3) and (3.14). and
and  ;
; and (3.13);
and (3.13); ;
;