- Research Article
- Open access
- Published:
Differential Inequalities for One Component of Solution Vector for Systems of Linear Functional Differential Equations
Advances in Difference Equations volume 2010, Article number: 478020 (2010)
Abstract
The method to compare only one component of the solution vector of linear functional differential systems, which does not require heavy sign restrictions on their coefficients, is proposed in this paper. Necessary and sufficient conditions of the positivity of elements in a corresponding row of Green's matrix are obtained in the form of theorems about differential inequalities. The main idea of our approach is to construct a first order functional differential equation for the  th component of the solution vector and then to use assertions about positivity of its Green's functions. This demonstrates the importance to study scalar equations written in a general operator form, where only properties of the operators and not their forms are assumed. It should be also noted that the sufficient conditions, obtained in this paper, cannot be improved in a corresponding sense and does not require any smallness of the interval
th component of the solution vector and then to use assertions about positivity of its Green's functions. This demonstrates the importance to study scalar equations written in a general operator form, where only properties of the operators and not their forms are assumed. It should be also noted that the sufficient conditions, obtained in this paper, cannot be improved in a corresponding sense and does not require any smallness of the interval  , where the system is considered.
, where the system is considered.
1. Introduction
Consider the following system of functional differential equations

where 
 are linear continuous operators,
are linear continuous operators,  and
and  are the spaces of continuous and summable functions
are the spaces of continuous and summable functions  , respectively.
, respectively.
Let  be a linear bounded functional. If the homogeneous boundary value problem
be a linear bounded functional. If the homogeneous boundary value problem  has only the trivial solution, then the boundary value problem
has only the trivial solution, then the boundary value problem

has for each  where
where  and
and  a unique solution, which has the following representation [1]:
a unique solution, which has the following representation [1]:

where the  matrix
matrix  is called Green's matrix of problem (1.2), and
is called Green's matrix of problem (1.2), and  is the
is the  fundamental matrix of the system
fundamental matrix of the system  such that
such that  (
( is the unit
is the unit  -matrix). It is clear from the solution representation (1.3) that the matrices
-matrix). It is clear from the solution representation (1.3) that the matrices  and
and  determine all properties of solutions.
determine all properties of solutions.
The following property is the basis of the approximate integration method by Tchaplygin [2]: from the conditions

it follows that

Series of papers, started with the known paper by Luzin [3], were devoted to the various aspects of Tchaplygin's approximate method. The well-known monograph by Lakshmikantham and Leela [4] was one of the most important in this area. The known book by Krasnosel'skii et al. [5] was devoted to approximate methods for operator equations. These ideas have been developing in scores of books on the monotone technique for approximate solution of boundary value problems for systems of differential equations. Note in this connection the important works by Kiguradze and Puza [6, 7] and Kiguradze [8].
As a particular case of system (1.1), let us consider the following delay system:

where  are summable functions, and
are summable functions, and  are measurable functions such that
are measurable functions such that  for
for 

The classical Wazewskii's theorem claims [9] that the condition

is necessary and sufficient for the property (1.4) (1.5) for the Cauchy problem for system of ordinary differential equations
(1.5) for the Cauchy problem for system of ordinary differential equations

From formula of solution representation (1.3), it is clear that property (1.4) (1.5) is true if all elements of the matrices
(1.5) is true if all elements of the matrices  and
and  are nonnegative.
are nonnegative.
We focus our attention upon the problem of comparison for only one of the components of solution vector. Let  be either 1 or 2. In this paper we consider the following property: from the conditions
be either 1 or 2. In this paper we consider the following property: from the conditions

it does follow that for a corresponding fixed component  of the solution vector the inequality
of the solution vector the inequality

is satisfied. This property is a weakening of the property (1.4) (1.5) and, as we will obtain below, leads to essentially less hard limitations on the given system. From formula of solution's representation (1.3), it follows that this property is reduced to sign-constancy of all elements standing only in the
(1.5) and, as we will obtain below, leads to essentially less hard limitations on the given system. From formula of solution's representation (1.3), it follows that this property is reduced to sign-constancy of all elements standing only in the  th row of Green's matrix.
th row of Green's matrix.
The main idea of our approach is to construct a corresponding scalar functional differential equation of the first order

for  th component of a solution vector, where
th component of a solution vector, where  is a linear continuous operator,
is a linear continuous operator, 
 This equation is built in Section 2. Then the technique of analysis of the first-order scalar functional differential equations, developed, for example, in the works [10–12], is used. On this basis in Section 3 we obtain necessary and sufficient conditions of nonpositivity/nonnegativity of elements in
This equation is built in Section 2. Then the technique of analysis of the first-order scalar functional differential equations, developed, for example, in the works [10–12], is used. On this basis in Section 3 we obtain necessary and sufficient conditions of nonpositivity/nonnegativity of elements in  th row of Green's matrices in the form of theorems about differential inequalities. Simple coefficient tests of the sign constancy of the elements in the
th row of Green's matrices in the form of theorems about differential inequalities. Simple coefficient tests of the sign constancy of the elements in the  th row of Green's matrices are proposed in Section 4 for systems of ordinary differential equations and in Section 5 for systems of delayed differential equations. It should be stressed that in our results a smallness of the interval
th row of Green's matrices are proposed in Section 4 for systems of ordinary differential equations and in Section 5 for systems of delayed differential equations. It should be stressed that in our results a smallness of the interval  is not assumed.
is not assumed.
Note that results of this sort for the Cauchy problem (i.e.,  ) and Volterra operators
) and Volterra operators  were proposed in the recent paper [13], where the obtained operator
were proposed in the recent paper [13], where the obtained operator  became a Volterra operator. In this paper we consider other boundary conditions that imply that the operator
became a Volterra operator. In this paper we consider other boundary conditions that imply that the operator  is not a Volterra one even in the case when all
is not a Volterra one even in the case when all  are Volterra operators.
are Volterra operators.
2. Construction of Equation for  th Component of Solution Vector
th Component of Solution Vector
In this paragraph, we consider the boundary value problem


where  are linear bounded operators for
are linear bounded operators for  and
and  , are linear boundary functionals
, are linear boundary functionals
Together with problem (2.1), (2.2) let us consider the following auxiliary problem consisting of the system:

of the order  and the boundary conditions
and the boundary conditions

Let us assume that problem (2.3), (2.4) is uniquely solvable; denote by  its Green's matrix and by
its Green's matrix and by  Green's matrix of the problem (2.1), (2.2).
Green's matrix of the problem (2.1), (2.2).
Let us start with the following assertion, explaining how the scalar functional differential equation for one of the components of the solution vector can be constructed.
Lemma 2.1.
The component  of the solution vector of system (2.1) satisfies the following scalar functional differential equation:
of the solution vector of system (2.1) satisfies the following scalar functional differential equation:

where the operator  and the function
and the function 
 are defined by the equalities
are defined by the equalities


where  is the solution of the system
is the solution of the system

satisfying condition (2.4).
Proof.
Using Green's matrix  of problem (2.3), (2.4), we obtain
of problem (2.3), (2.4), we obtain

for every  Substitution of these representations in the
Substitution of these representations in the  th equation of the system (2.1) leads to (2.5), where the operator
th equation of the system (2.1) leads to (2.5), where the operator  and the function
and the function  are described by formulas (2.6) and (2.7), respectively.
are described by formulas (2.6) and (2.7), respectively.
3. Positivity of the Elements in the Fixed  th Row of Green's Matrices
th Row of Green's Matrices
Consider the boundary value problem

where  are linear continuous operators for
are linear continuous operators for 
Theorem 3.1.
Let problem (2.3), (2.4) be uniquely solvable, all elements of its (  Green's matrix
Green's matrix  nonnegative, and the operators
nonnegative, and the operators  and
and  positive operators for
positive operators for  Then the following 2 assertions are equivalent:
Then the following 2 assertions are equivalent:
-
(1)
there exists an absolutely continuous vector function
 such that
such that 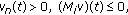 for
for 
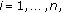 and the solution of the homogeneous equation (
and the solution of the homogeneous equation (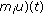
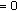 for
for  satisfying the conditions
satisfying the conditions 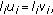
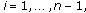 is nonpositive;
is nonpositive; -
(2)
the boundary value problem (3.1) is uniquely solvable for every summable
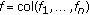 and
and  and elements of the nth row of its Green's matrix satisfy the inequalities:
and elements of the nth row of its Green's matrix satisfy the inequalities: 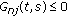 for
for 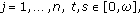 while
while  for
for 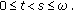
Proof.
Let us start with the implication  By virtue of Lemma 2.1, the component
By virtue of Lemma 2.1, the component  of the solution vector of problem (3.1) satisfies (2.5). Condition
of the solution vector of problem (3.1) satisfies (2.5). Condition  by virtue of Theorem
by virtue of Theorem  of the paper [14] implies that Green's function G
of the paper [14] implies that Green's function G of the boundary value problem
of the boundary value problem

exists and satisfies the inequalities  for
for  while
while  for
for  . Lemma 2.1, the representations of solutions of boundary value problem (3.1) and the scalar one-point problem (3.2) imply the equality
. Lemma 2.1, the representations of solutions of boundary value problem (3.1) and the scalar one-point problem (3.2) imply the equality

If  is a negative operator for every
is a negative operator for every  and
and  for
for  then
then  The nonpositivity of
The nonpositivity of  implies that
implies that  is nonnegative and consequently
is nonnegative and consequently  for
for  and
and 
If we set  for
for  and
and  for
for  then
then

and it is clear that  It is known from Theorem
It is known from Theorem  of the paper [14] that
of the paper [14] that  for
for  This implies that
This implies that  for
for 
In order to prove  , let us define
, let us define  (
( by the following way:
by the following way:

where  (
( is a solution to the problem
is a solution to the problem

It is clear that the functions  (
( satisfy the homogeneous system
satisfy the homogeneous system

and  for
for 
Theorem 3.2.
Let problem (2.3), (2.4) be uniquely solvable, all elements of its (  Green's matrix
Green's matrix  nonpositive, and
nonpositive, and  and
and  positive operators for
positive operators for  Then the following 2 assertions are equivalent:
Then the following 2 assertions are equivalent:
-
(1*)
there exists an absolutely continuous vector function
 such that
such that 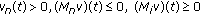 for
for 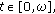
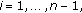 and the solution of the homogeneous equation (
and the solution of the homogeneous equation (
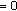 for
for 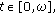
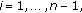 satisfying the conditions
satisfying the conditions 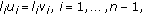 is nonnegative;
is nonnegative; -
(2*)
the boundary value problem (3.1) is uniquely solvable for every summable
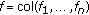 and
and 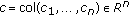 and elements of the nth row of its Green's matrix satisfies the inequalities:
and elements of the nth row of its Green's matrix satisfies the inequalities:  for
for 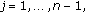
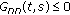 for
for 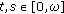 while
while  for
for 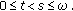
The proof of this theorem is analogous to the proof of Theorem 3.1.
4. Sufficient Conditions of Nonpositivity of the Elements in the th Row of Green's Matrices for System of Ordinary Differential Equations
th Row of Green's Matrices for System of Ordinary Differential Equations
In this paragraph, we consider the system of the ordinary differential equations

with the boundary conditions

Theorem 4.1.
Let the following conditions be fulfilled:
-
(1)
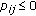 for
for 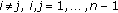 ;
; -
(2)
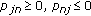 for
for 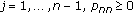 ;
; -
(3)
there exists a positive number
 such that
such that  (4.3)
(4.3)
Then problem (4.1), (4.2) is uniquely solvable for every summable 
 and
and  and the elements of the
and the elements of the  th row of Green's matrix of boundary value problem (4.1), (4.2) satisfy the inequalities:
th row of Green's matrix of boundary value problem (4.1), (4.2) satisfy the inequalities:  for
for  for
for 
 for
for 
Proof.
Let us prove that all elements of Green's matrix  of the auxiliary boundary value problem
of the auxiliary boundary value problem

are nonnegative. The conditions  ,
,  , and the inequality
, and the inequality

imply that the conditions  and
and  of Theorem
of Theorem  of the paper [13] are fulfilled. Assertion (a) of Theorem
of the paper [13] are fulfilled. Assertion (a) of Theorem  [13] is fulfilled. To prove it, we set
[13] is fulfilled. To prove it, we set  for
for  in this assertion. Now according to equivalence of assertions (a) and (b) in Theorem
in this assertion. Now according to equivalence of assertions (a) and (b) in Theorem  of the paper [13], we get the nonnegativity of all elements of its Green's matrix
of the paper [13], we get the nonnegativity of all elements of its Green's matrix 
Let us set  for
for  and
and  in the condition
in the condition  of Theorem 3.1. We obtain that this condition is satisfied if
of Theorem 3.1. We obtain that this condition is satisfied if  satisfies the following system of the inequalities:
satisfies the following system of the inequalities:

Now by virtue of Theorem 3.1, all elements of the  th row of Green's matrix satisfy the inequalities
th row of Green's matrix satisfy the inequalities  for
for  and, using [14], we can conclude that
and, using [14], we can conclude that  for
for  .
.
Consider now the following ordinary differential system of the second order;

with the conditions

From Theorem 4.1 as a particular case for  , we obtain the following assertion.
, we obtain the following assertion.
Theorem 4.2.
Let the following two conditions be fulfilled:
-
(1)
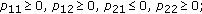
-
(2)
there exists a positive
 such that
such that 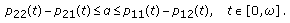 (4.9)
(4.9)
Then problem (4.7), (4.8) is uniquely solvable for every summable  and
and  and the elements of the second row of Green's matrix of problem (4.7), (4.8) satisfy the inequalities:
and the elements of the second row of Green's matrix of problem (4.7), (4.8) satisfy the inequalities:  for
for 
 for
for 
Remark 4.3.
If coefficients  are constants, the second condition in Theorem 4.2 is as follows:
are constants, the second condition in Theorem 4.2 is as follows:

Remark 4.4.
Let us demonstrate that inequality (4.10) is best possible in a corresponding case and the condition

cannot be set instead of (4.10). The characteristic equation of the system

with constant coefficients is as follows:

If we set 
 ,
,  then the roots are
then the roots are  ,
,  and the problem
and the problem

has nontrivial solution for 
5. Sufficient Conditions of Nonpositivity of the Elements in the  th Row of Green's Matrices for Systems with Delay
th Row of Green's Matrices for Systems with Delay
Let us consider the system of the delay differential equations


with the boundary conditions

We introduce the denotations:  ,
,  ,
,  , and
, and 
Theorem 5.1.
Let the following conditions be fulfilled:
-
(1)
 for
for 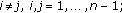
-
(2)
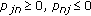 for
for 
-
(3)
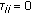 for
for 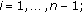
-
(4)
there exists a positive number
 such that
such that

Then problem (5.1), (5.3) is uniquely solvable for every summable 
 and
and  and the elements of the
and the elements of the  th row of Green's matrix of problem (5.1), (5.3) satisfy the inequalities:
th row of Green's matrix of problem (5.1), (5.3) satisfy the inequalities:  for
for 
 for
for 
Proof.
Repeating the explanations in the beginning of the proof of Theorem 4.1, we can obtain on the basis of Theorem  of the paper [13] that all the elements of
of the paper [13] that all the elements of  Green's matrix
Green's matrix  of the auxiliary problem, consisting of the system
of the auxiliary problem, consisting of the system

and the boundary conditions  are nonnegative.
are nonnegative.
Let us set  for
for  and
and  in the condition (
in the condition ( ) of Theorem 3.1. We obtain that the condition (
) of Theorem 3.1. We obtain that the condition ( ) of Theorem 3.1 is satisfied if
) of Theorem 3.1 is satisfied if  satisfies the following system of the inequalities:
satisfies the following system of the inequalities:


Now by virtue of Theorem 3.1, all elements of the  th row of Green's matrix of problem (5.1), (5.3) satisfy the inequalities
th row of Green's matrix of problem (5.1), (5.3) satisfy the inequalities  for
for while
while  for
for 
Remark 5.2.
It was explained in the previous paragraph that in the case of ordinary system ( with constant coefficients
with constant coefficients  , inequality (5.4) is best possible in a corresponding case.
, inequality (5.4) is best possible in a corresponding case.
Let us consider the second-order scalar differential equation

where  for
for  with the boundary conditions
with the boundary conditions

and the corresponding differential system of the second order

where  for
for  with the boundary conditions
with the boundary conditions

It should be noted that the element  of Green's matrix of system (5.10), (5.11) coincides with Green's function
of Green's matrix of system (5.10), (5.11) coincides with Green's function  of the problem (5.8), (5.9) for scalar second-order equation.
of the problem (5.8), (5.9) for scalar second-order equation.
Theorem 5.3.
Assume that  and there exists a positive number
and there exists a positive number  such that
such that

Then problem (5.10), (5.11) is uniquely solvable for every summable  and
and  and the elements of the second row of Green's matrix of this problem satisfy the inequalities:
and the elements of the second row of Green's matrix of this problem satisfy the inequalities: 
 while
while  for
for 
In order to prove Theorem 5.3, we set  in the assertion (
in the assertion ( ) of Theorem 3.1.
) of Theorem 3.1.
Remark 5.4.
Inequality (5.12) is best possible in the following sense. Let us add  in its right hand side. We get that the inequality
in its right hand side. We get that the inequality

and the assertion of Theorem 5.3 is not true. Let us set that coefficients are constants:  and
and  It is clear that the inequality (5.13) is fulfilled if we set
It is clear that the inequality (5.13) is fulfilled if we set  small enough. Consider the following homogeneous boundary value problem:
small enough. Consider the following homogeneous boundary value problem:

The components  of the solution vector are periodic and for
of the solution vector are periodic and for  the boundary value problem (5.14) has a nontrivial solution.
the boundary value problem (5.14) has a nontrivial solution.
Let us prove the following assertions, giving an efficient test of nonpositivity of the elements in the  th row of Green's matrix in the case when the coefficients
th row of Green's matrix in the case when the coefficients  are small enough for
are small enough for 
Theorem 5.5.
Let the following conditions be fulfilled:
-
(1)
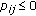 for
for 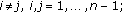
-
(2)
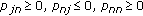 for
for 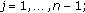
-
(3)
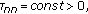 and other delays
and other delays 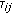 are zeros;
are zeros; -
(4)
the inequalities


are fulfilled.
Then problem (5.1), (5.3) is uniquely solvable for every summable  and
and  , and the elements of the
, and the elements of the  th row of its Green's matrix satisfy the inequalities:
th row of its Green's matrix satisfy the inequalities:  for
for  while
while  for
for 
Proof.
Let us set  for
for  and
and  in the condition
in the condition  of Theorem 3.1.
of Theorem 3.1.

In the left-hand side, we have the inequality

which is fulfilled when

The right-hand side in inequality (5.18) gets its maximum for  Substituting this
Substituting this  into (5.19) and the right part of (5.17), we obtain inequalities (5.15) and (5.16).
into (5.19) and the right part of (5.17), we obtain inequalities (5.15) and (5.16).
Remark 5.6.
It can be stressed that we do not require a smallness of the interval  in Theorems 5.1–5.5.
in Theorems 5.1–5.5.
Remark 5.7.
It can be noted that inequality (5.15) is best possible in the following sense. If  for
for 
 then system (5.1) and inequality (5.15) become of the following forms:
then system (5.1) and inequality (5.15) become of the following forms:


respectively. The opposite to (5.21) inequality  implies oscillation of all solutions [15] of the equation
implies oscillation of all solutions [15] of the equation

It implies that the homogeneous problem

has nontrivial solutions for corresponding  Now it is clear that we cannot substitute
Now it is clear that we cannot substitute

where  is any positive number instead of inequality (5.15).
is any positive number instead of inequality (5.15).
References
Azbelev NV, Maksimov VP, Rakhmatullina LF: Introduction to the Theory of Functional Differential Equations, Advanced Series in Mathematics Science and Engineering. Volume 3. World Federation, Atlanta, Ga, USA; 1995.
Tchaplygin SA: New Method of Approximate Integration of Differential Equations. GTTI, Moscow, UK; 1932.
Luzin NN: On the method of approximate integration of academician S. A. Tchaplygin. Uspekhi Matematicheskikh Nauk 1951,6(6):3-27.
Lakshmikantham V, Leela S: Differential and Integral Inequalities. Academic Press; 1969.
Krasnosel'skii MA, Vainikko GM, Zabreiko PP, Rutitskii JaB, Stezenko VJa: Approximate Methods for Solving Operator Equations. Nauka, Moscow, Russia; 1969.
Kiguradze I, Puza B: On boundary value problems for systems of linear functional-differential equations. Czechoslovak Mathematical Journal 1997,47(2):341-373. 10.1023/A:1022829931363
Kiguradze I, Puza B: Boundary Value Problems for Systems of Linear Functional Differential Equations, Folia Facultatis Scientiarium Naturalium Universitatis Masarykianae Brunensis. Mathematica. Volume 12. FOLIA, Masaryk University, Brno, Czech Republic; 2003:108.
Kiguradze IT: Boundary value problems for systems of ordinary differential equations. In Current Problems in Mathematics. Newest Results, Itogi Nauki i Tekhniki. Volume 30. Akad. Nauk SSSR Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, Russia; 1987:3-103. English translated in Journal of Soviet Mathematics, vol. 43, no. 2, 2259–2339, 1988
Ważewski T: Systèmes des équations et des inégalités différentielles ordinaires aux deuxièmes membres monotones et leurs applications. Annales Polonici Mathematici 1950, 23: 112-166.
Agarwal RP, Domoshnitsky A: Non-oscillation of the first-order differential equations with unbounded memory for stabilization by control signal. Applied Mathematics and Computation 2006,173(1):177-195. 10.1016/j.amc.2005.02.062
Domoshnitsky A: Maximum principles and nonoscillation intervals for first order Volterra functional differential equations. Dynamics of Continuous, Discrete & Impulsive Systems A 2008,15(6):769-814.
Hakl R, Lomtatidze A, Sremr J: Some Boundary Value Problems for First Order Scalar Functional Differential Equations. FOLIA, Masaryk University, Brno, Czech Republic; 2002.
Agarwal RP, Domoshnitsky A: On positivity of several components of solution vector for systems of linear functional differential equations. Glasgow Mathematical Journal 2010,52(1):115-136. 10.1017/S0017089509990218
Domoshnitsky A: New concept in the study of differential inequalities. In Functional-Differential Equations, Functional Differential Equations, Israel Seminar. Volume 1. The College of Judea & Samaria, Ariel, Israel; 1993:52-59.
Győri I, Ladas G: Oscillation Theory of Delay Differential Equations, Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York, NY, USA; 1991:xii+368.
Acknowledgments
The author thanks the referees for their available remarks. This research was supported by The Israel Science Foundation (Grant no. 828/07).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Domoshnitsky, A. Differential Inequalities for One Component of Solution Vector for Systems of Linear Functional Differential Equations. Adv Differ Equ 2010, 478020 (2010). https://doi.org/10.1155/2010/478020
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/478020
 th Component of Solution Vector
th Component of Solution Vector th Row of Green's Matrices
th Row of Green's Matrices such that
such that 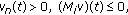 for
for 
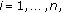 and the solution of the homogeneous equation (
and the solution of the homogeneous equation (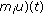
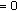 for
for  satisfying the conditions
satisfying the conditions 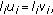
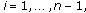 is nonpositive;
is nonpositive;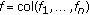 and
and  and elements of the nth row of its Green's matrix satisfy the inequalities:
and elements of the nth row of its Green's matrix satisfy the inequalities: 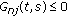 for
for 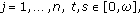 while
while  for
for 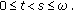
 such that
such that 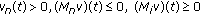 for
for 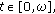
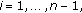 and the solution of the homogeneous equation (
and the solution of the homogeneous equation (
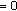 for
for 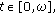
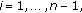 satisfying the conditions
satisfying the conditions 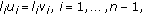 is nonnegative;
is nonnegative;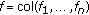 and
and 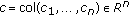 and elements of the nth row of its Green's matrix satisfies the inequalities:
and elements of the nth row of its Green's matrix satisfies the inequalities:  for
for 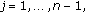
 for
for 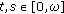 while
while  for
for 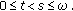
 th Row of Green's Matrices for System of Ordinary Differential Equations
th Row of Green's Matrices for System of Ordinary Differential Equations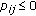 for
for 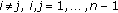 ;
;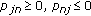 for
for 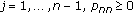 ;
; such that
such that 
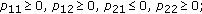
 such that
such that 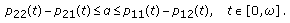
 th Row of Green's Matrices for Systems with Delay
th Row of Green's Matrices for Systems with Delay for
for 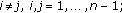
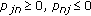 for
for 
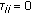 for
for 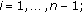
 such that
such that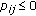 for
for 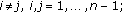
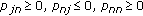 for
for 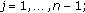
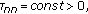 and other delays
and other delays 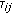 are zeros;
are zeros;