- Research Article
- Open access
- Published:
Uniqueness of Periodic Solution for a Class of Liénard 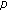 -Laplacian Equations
-Laplacian Equations
Advances in Difference Equations volume 2010, Article number: 235749 (2010)
Abstract
By topological degree theory and some analysis skills, we consider a class of generalized Liénard type  -Laplacian equations. Upon some suitable assumptions, the existence and uniqueness of periodic solutions for the generalized Liénard type
-Laplacian equations. Upon some suitable assumptions, the existence and uniqueness of periodic solutions for the generalized Liénard type  -Laplacian differential equations are obtained. It is significant that the nonlinear term contains two variables.
-Laplacian differential equations are obtained. It is significant that the nonlinear term contains two variables.
1. Introduction
As it is well known, the existence of periodic and almost periodic solutions is the most attracting topics in the qualitative theory of differential equations due to their vast applications in physics, mathematical biology, control theory, and others. More general equations and systems involving periodic boundary conditions have also been considered. Especially, the existence of periodic solutions for the Duffing equation, Rayleigh equation, and Liénard type equation, which are derived from many fields, such as fluid mechanics and nonlinear elastic mechanics, has received a lot of attention.
Many experts and scholars, such as Manásevich, Mawhin, Gaines, Cheung, Ren, Ge, Lu, and Yu, have contributed a series of existence results to the periodicity theory of differential equations. Fixed point theory, Mawhin's continuation theorem, upper and lower solutions method, and coincidence degree theory are the common tools to study the periodicity theory of differential equations. Among these approaches, the Mawhin's continuation theorem seems to be a very powerful tool to deal with these problems.
Some contributions on periodic solutions to differential equations have been made in [1–13]. Recently, periodic problems involving the scalar  -Laplacian were studied by many authors. We mention the works by Manásevich and Mawhin [3] and Cheung and Ren [4, 8, 10].
-Laplacian were studied by many authors. We mention the works by Manásevich and Mawhin [3] and Cheung and Ren [4, 8, 10].
In [3], Manásevich and Mawhin investigated the existence of periodic solutions to the boundary value problem

where the function  is quite general and satisfies some monotonicity conditions which ensure that
is quite general and satisfies some monotonicity conditions which ensure that  is homeomorphism onto
is homeomorphism onto  Applying Leray-Schauder degree theory, the authors brought us the widely used Manásevich-Mawhin continuation theorem. When
Applying Leray-Schauder degree theory, the authors brought us the widely used Manásevich-Mawhin continuation theorem. When  is the so-called one-dimensional p-Laplacian operator given by
is the so-called one-dimensional p-Laplacian operator given by 
Recently, by Mawhin's continuation theorem, Cheung and Ren studied the existence of  -periodic solutions for a
-periodic solutions for a  -Laplacian Liénard equation with a deviating argument in [4] as follows:
-Laplacian Liénard equation with a deviating argument in [4] as follows:

and two results (Theorems 3.1 and 3.2 ) on the existence of periodic solutions were obtained.
Ge and Ren [5] promoted Mawhin's continuation theorem to the case which involved the quasilinear operator successfully; this also prepared conditions for using Mawhin's continuation theorem to solve nonlinear boundary value problem.
Liu [7] has dealt with the existence and uniqueness of  -periodic solutions of the Liénard type
-periodic solutions of the Liénard type  -Laplacian differential equation of the form
-Laplacian differential equation of the form

by using topological degree theory, and one sufficient condition for the existence and uniqueness of  -periodic solutions of this equation was established.
-periodic solutions of this equation was established.
The aim of this paper is to study the existence of periodic solutions to a class of  -Laplacian Liénard equations as follows:
-Laplacian Liénard equations as follows:

where  ,
,  is given by
is given by  for
for  ,
,  ,
,  ,
,  and
and  -periodic in the first variable, where
-periodic in the first variable, where  is a given constant,
is a given constant,  and
and 
The paper is organized as follows. In Section 2, we give the definition of norm in Banach space and the main lemma. In Section 3, combining Lemma 2.1 with some analysis skills, two sufficient conditions about the existence of solutions for (1.4) are obtained. The nonlinear terms  and
and  contain two variables in this paper, which is seldom considered in the other papers, and the results are new.
contain two variables in this paper, which is seldom considered in the other papers, and the results are new.
2. Preliminary Results
For convenience, we define

and the norm  is defined by
is defined by  , for all
, for all 

Clearly,  is a Banach space endowed with such norm.
is a Banach space endowed with such norm.
For the periodic boundary value problem

where  is a continuous function and
is a continuous function and  -periodic in the first variable, we have the following result.
-periodic in the first variable, we have the following result.
Lemma 2.1 (see [3]).
Let  be an open bounded set in
be an open bounded set in  . If the following conditions hold:
. If the following conditions hold:
-
(i)
for each
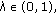 the problem
the problem 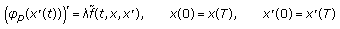 (2.4)
(2.4)has no solution on
 ,
, -
(ii)
the equation
 (2.5)
(2.5)has no solution on
 ,
, -
(iii)
the Brouwer degree of
 is
is 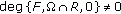 ,
,
then the periodic boundary value problem (2.3) has at least one  -periodic solution on
-periodic solution on 
Set

We can rewrite (1.4) in the following form:

where  and
and 
Lemma 2.2.
Suppose the following condition holds:
(A1)  , for all
, for all  .
.
Then (1.4) has at most one  -periodic solution.
-periodic solution.
Proof.
Let  and
and  be two
be two  -periodic solutions of (1.4). Then, from (2.7), we obtain
-periodic solutions of (1.4). Then, from (2.7), we obtain

Set

Then it follows from (2.8) that

We claim that  for all
for all  By way of contradiction, in view of
By way of contradiction, in view of  and
and  for all
for all  , we obtain
, we obtain  Then there must exist
Then there must exist  ; for convenience, we can choose
; for convenience, we can choose  such that
such that

which implies that

Set

Then,  Since
Since  , if
, if  from the first equation of (2.12), we have
from the first equation of (2.12), we have

which contradicts assumption  , so
, so  ; it implies that
; it implies that  that is,
that is,  Hence we have
Hence we have

Substituting (2.15) into the second equation of (2.12), we have

Noticing ( ) and that
) and that  and
and  , from (2.16), we know that
, from (2.16), we know that

this contradicts the second equation of (2.12). So we have  , for all
, for all 
By using a similar argument, we can also show that

Then, from (2.10) we obtain

For every  if
if  then it contradicts (2.19), so
then it contradicts (2.19), so  ; it implies that
; it implies that  then
then  , for all
, for all 
Hence, (1.4) has at most one  -periodic solution. The proof of Lemma 2.2 is completed now.
-periodic solution. The proof of Lemma 2.2 is completed now.
3. Main Results
Theorem 3.1.
Let ( ) hold. Suppose that there exists a positive constant d such that
) hold. Suppose that there exists a positive constant d such that
(A2)  , for all
, for all 
(A3) 
Then (1.4) has one unique  -periodic solution if
-periodic solution if 
Proof.
Consider the homotopic equation of (1.4) as follows:

By Lemma 2.2, combining  it is easy to see that (1.4) has at least one
it is easy to see that (1.4) has at least one  -periodic solution. For the remainder, we will apply Lemma 2.1 to study (3.1). Firstly, we will verify that all the possible
-periodic solution. For the remainder, we will apply Lemma 2.1 to study (3.1). Firstly, we will verify that all the possible  -periodic solutions of (3.1) are bounded.
-periodic solutions of (3.1) are bounded.
Let  be an arbitrary solution of (3.1) with period
be an arbitrary solution of (3.1) with period  . By integrating the two sides of (3.1) from
. By integrating the two sides of (3.1) from  to
to  and
and  we obtain
we obtain

Consider  and
and  , there exists
, there exists  such that
such that  while for
while for  we see that
we see that

where  Let
Let  be the global maximum point of
be the global maximum point of  on
on  Then as
Then as  we claim that
we claim that

Otherwise, we have  there must exist a constant
there must exist a constant  such that
such that  , for
, for  ; therefore,
; therefore,  is strictly increasing for
is strictly increasing for  which implies that
which implies that  is strictly increasing for
is strictly increasing for  Thus, (3.4) is true. Then
Thus, (3.4) is true. Then

In view of ( ), (3.5) implies that
), (3.5) implies that  ; similar to the global minimum point of
; similar to the global minimum point of  on
on  Since
Since  it follows that there exists a constant
it follows that there exists a constant  such that
such that  Then we have
Then we have

Combining the above two inequalities, we obtain

Considering ( )
) there exist constants
there exist constants  and the sufficiently small
and the sufficiently small  such that
such that

Set

From (3.7), we have

where  Combining the classical inequality
Combining the classical inequality  when
when  where
where  is a constant, since
is a constant, since

then we consider the following two cases.
Case 1.
If  then
then  Combining (3.7), we know that
Combining (3.7), we know that

when  then we have
then we have 
Case 2.
When  then from the above classical inequality, we obtain
then from the above classical inequality, we obtain

Substituting the above inequality into (3.10) we get
we get

Since  is
is  -periodic, multiplying
-periodic, multiplying  by (3.1) and then integrating from
by (3.1) and then integrating from  to
to  , in view of (
, in view of ( )
) we have
we have

Substituting (3.14) into (3.15) and since

we obtain

where

Since  and
and  from (3.17), we know that there exists a constant
from (3.17), we know that there exists a constant  such that
such that  Then,
Then,

So, there exists a constant such that

Set

Then (3.1) has no solution on  as
as  and when
and when  or
or  ; from
; from  we can see that
we can see that

so condition (ii) holds.
Set

Then, when  ,
,  we have
we have

thus  is a homotopic transformation and
is a homotopic transformation and

So condition (iii) holds. In view of Lemma 2.1, there exists at least one solution with period  . This completes the proof.
. This completes the proof.
Theorem 3.2.
Let ( ) hold. Suppose that there exist positive constants
) hold. Suppose that there exist positive constants  and
and  satisfying the following conditions:
satisfying the following conditions:
(A4)  , when
, when 
(A5)  ,
, 
(A6)  , when
, when
Then for (1.4) there exists one unique  -periodic solution when
-periodic solution when 
Proof.
We can rewrite (3.1) in the following from:

Let  be a
be a  -periodic solution of (3.26), then
-periodic solution of (3.26), then  must be a
must be a  -periodic solution of (3.1). First we claim that there is a constant
-periodic solution of (3.1). First we claim that there is a constant  such that
such that

Take  as the global maximum point and global minimum point of
as the global maximum point and global minimum point of  on
on  , respectively, then
, respectively, then

From the first equation of (3.26) we have  so
so 
We claim that

By way of contradiction, (3.29) does not hold, then  So there exists
So there exists  such that
such that  , for
, for  ; therefore,
; therefore,  , for
, for  so
so  ,
,  that is,
that is,  , for
, for  This contradicts the definition of
This contradicts the definition of  so we have
so we have 
Substituting  into the second equation of (3.26), we obtain
into the second equation of (3.26), we obtain

By condition ( )
) we have
we have  Similarly, we get
Similarly, we get 
Case 1.
If  define
define  Obviously
Obviously 
Case 2.
If  from the fact that
from the fact that  is a continuous function in
is a continuous function in  there exists a constant
there exists a constant  between
between  and
and  such that
such that 
So we have that (3.27) holds. Next, in view of  there are integer
there are integer  and constant
and constant  such that
such that  hence
hence 
So

We claim that all the periodic solutions  of (3.1) are bounded and
of (3.1) are bounded and 
Let

Multiplying both sides of (3.1) by  and integrating from
and integrating from  to
to  together with (
together with ( ) and (
) and ( ), we have
), we have

where  and
and  That is,
That is,

Using Hölder's inequality and  we have
we have

so

there must be a positive constant  such that
such that

hence together with (3.31), we have 
This proves the claim and that the rest of the proof of the theorem is identical to that of Theorem 3.1.
References
Lu S:Existence of periodic solutions to a
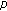 -Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041
-Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041Xiao B, Liu B:Periodic solutions for Rayleigh type
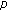 -Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010
-Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010Manásevich R, Mawhin J:Periodic solutions for nonlinear systems with
 -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425Cheung W-S, Ren J:On the existence of periodic solutions for
 -Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75.
-Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75.Ge W, Ren J:An extension of Mawhin's continuation theorem and its application to boundary value problems with a
 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2004,58(3-4):477-488. 10.1016/j.na.2004.01.007
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2004,58(3-4):477-488. 10.1016/j.na.2004.01.007Zhang F, Li Y:Existence and uniqueness of periodic solutions for a kind of Duffing type
 -Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013
-Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013Liu B:Existence and uniqueness of periodic solutions for a kind of Liénard type
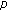 -Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007
-Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007Cheung W-S, Ren J:Periodic solutions for
 -Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120.
-Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120.Gaines RE, Mawhin JL: Coincidence Degree, and Nonlinear Differential Equations, Lecture Notes in Mathematics. Volume 568. Springer, Berlin, Germany; 1977:i+262.
Cheung W-S, Ren J:Periodic solutions for
 -Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002
-Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002Peng S, Zhu S:Periodic solutions for
 -Laplacian Rayleigh equations with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2007,67(1):138-146. 10.1016/j.na.2006.05.007
-Laplacian Rayleigh equations with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2007,67(1):138-146. 10.1016/j.na.2006.05.007Cao F, Han Z, Sun S:Existence of periodic solutions for
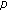 -Laplacian equations on time scales. Advances in Difference Equations 2010, 2010:-13.
-Laplacian equations on time scales. Advances in Difference Equations 2010, 2010:-13.Cao F, Han Z:Existence of periodic solutions for
 -Laplacian differential equation with a deviating arguments. Journal of University of Jinan (Sci. Tech.) 2010,24(1):95-98.
-Laplacian differential equation with a deviating arguments. Journal of University of Jinan (Sci. Tech.) 2010,24(1):95-98.
Acknowledgments
The authors sincerely thank the reviewers for their valuable suggestions and useful comments that have led to the present improved version of the original manuscript. This research is supported by the Natural Science Foundation of China (60774004, 60904024), China Postdoctoral Science Foundation Funded Project (20080441126, 200902564), Shandong Postdoctoral Funded Project (200802018), and the Natural Scientific Foundation of Shandong Province (Y2008A28, ZR2009AL003) and is also supported by University of Jinan Research Funds for Doctors (XBS0843).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cao, F., Han, Z., Zhao, P. et al. Uniqueness of Periodic Solution for a Class of Liénard 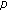 -Laplacian Equations.
Adv Differ Equ 2010, 235749 (2010). https://doi.org/10.1155/2010/235749
-Laplacian Equations.
Adv Differ Equ 2010, 235749 (2010). https://doi.org/10.1155/2010/235749
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/235749
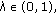 the problem
the problem 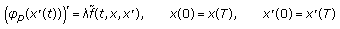
 ,
,
 ,
, is
is 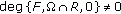 ,
, -Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041
-Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041 -Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010
-Laplacian equation with a deviating argument. Nonlinear Analysis: Real World Applications 2009,10(1):16-22. 10.1016/j.nonrwa.2007.08.010 -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425 -Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75.
-Laplacian generalized Liénard equation. Nonlinear Analysis: Theory, Methods & Applications 2005,60(1):65-75. -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2004,58(3-4):477-488. 10.1016/j.na.2004.01.007
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2004,58(3-4):477-488. 10.1016/j.na.2004.01.007 -Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013
-Laplacian equation. Nonlinear Analysis: Real World Applications 2008,9(3):985-989. 10.1016/j.nonrwa.2007.01.013 -Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007
-Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007 -Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120.
-Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120. -Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002
-Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002 -Laplacian Rayleigh equations with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2007,67(1):138-146. 10.1016/j.na.2006.05.007
-Laplacian Rayleigh equations with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2007,67(1):138-146. 10.1016/j.na.2006.05.007 -Laplacian equations on time scales. Advances in Difference Equations 2010, 2010:-13.
-Laplacian equations on time scales. Advances in Difference Equations 2010, 2010:-13. -Laplacian differential equation with a deviating arguments. Journal of University of Jinan (Sci. Tech.) 2010,24(1):95-98.
-Laplacian differential equation with a deviating arguments. Journal of University of Jinan (Sci. Tech.) 2010,24(1):95-98.