- Research Article
- Open access
- Published:
Switching Controller Design for a Class of Markovian Jump Nonlinear Systems Using Stochastic Small-Gain Theorem
Advances in Difference Equations volume 2009, Article number: 896218 (2009)
Abstract
Switching controller design for a class of Markovian jump nonlinear systems with unmodeled dynamics is considered in this paper. Based on the differential equation and infinitesimal generator of jump systems, the concept of Jump Input-to-State practical Stability (JISpS) in probability and stochastic Lyapunov stability criterion are put forward. By using backsetpping technology and stochastic small-gain theorem, a switching controller is proposed which ensures JISpS in probability for the jump nonlinear system. A simulation example illustrates the validity of this design.
1. Introduction
Stability of dynamic systems has been the primary study topic for system analysis. After Lyapunov's second method was created in 1892, it has been developed and applied by many researchers in the past century with fruitful classical stability results achieved. Among these important developments is the Input-to-State Stability (ISS) property, which was firstly formulated by Sontag [1] and has found wide use in engineering by incorporating the idea of nonlinear small-gain theorem [2, 3]. The ISS-based small-gain theorem has some advantages over the earlier passivity-based small-gain theorem and is currently becoming a desirable tool for nonlinear stability analysis, especially in the case of nonlinear robust stabilization for systems with nonlinear uncertainties and unmodeled dynamics [4, 5]. Among all the practical nonlinear systems with uncertainties, the systems of lower-triangular form are of great importance; such systems have several special properties so that they are recently attracting great attention. Firstly, the "lower-triangular" form has close connection with feedback linearzation method; therefore this provides convenience to designers. Second, many real-world dynamic systems are of lower-triangular form [6, 7], and some general systems can be transformed to lower-triangular form via mathematical method [8]. For this reason, lower-triangle nonlinear system can find its wide applications in lots of practical dynamic systems: turbine generator and water turbing generator [9], intelligent robot [10] and missile [11], and so forth. However, dynamic processes in this field are very difficult to describe exactly and depend on many factors. For example, imagining an attacking missile tracking a moving target, this dynamic process is a classical problem of model following and tracking; till now, different control algorithms have been put forward by using ideal assumptions [12, 13]. However, the missile itself may have variable structures subject to random changes and/or failures of its components or environments during its flight; such problems also occur in the case of the moving of robots or the operation of generators. Therefore, an urgent requirement appears to remodel such dynamic processes to meet the need of accuracy and precision.
On the other hand, Markovian jump systems, which were firstly put forward by Kac and Krasovskii [14], have now become convenient tools for representing many real-world systems [15, 16] and therefore arouse much research attention in recent years. In the case of fault detection, fault-tolerant control, and multimodal control, discrete jumps in the continuous dynamics are used to model component failures and sudden switch of system dynamics. With further study of Markovian jump systems, many achievements have been made in the last decade, among which Shaikhet and Mao performed foundational work on stochastic stability for jump systems [17–19] and jump systems with time delays [20–23]. Based on the stochastic stability, more efforts are devoted to applications of jump system model: system state estimation [24, 25], controller design [26–28], and hierarchical reinforcement learning for model-free jump systems [29, 30]. However, in the referred works concerned with controller design problems, assumptions are firstly made that system models considered only consist of static uncertainty. This is an ideal approximation of real situation and not the case nevertheless. As we know, Markovian jump systems are used to represent a class of systems which are usually accompanied by sudden change of working environment or system dynamics. For this reason, practical jump systems are usually accompanied by uncertainties, and it is hard to describe these uncertainties, with precise mathematical model. Thus, how to stabilize Markovian jump systems with unmodeled dynamic uncertainties is a concernful work in our view.
In this paper, we focus on the switching controller design for a class of Markovian jump nonlinear systems with dynamic uncertainties. The control strategy ensures robustness property of systems in the presentence of dynamic uncertainties. And our main contributions are composed of three aspects.
-
(i)
Stochastic differential equation for Markovian jump system is given according to generalized Itô formula, and the similar result is achieved by Yuan and Mao [19] with a different method. Based on differential equation, the martingale process caused by Markovian process is incarnated in the procedure of controller design by applying mathematical transform.
-
(ii)
We introduce the concept of Jump Input-to-State practical Stability (JISpS) and give stochastic Lyapunov stability criterion.
-
(iii)
By composing backstepping technology and stochastic small-gain theorem, a switching controller is proposed. It is shown that all signals of the closed-loop system are globally uniformly ultimately bounded. And the closed-loop system is JISpS in probability.
The rest of this paper is organized as follows. Section 2 begins with some mathematical notions and Markovian jump system model along with its differential equation. In Section 3, we introduce the notion of JISpS and stochastic Lyapunov stability criterion. Section 4 presents the problem description. In Section 5, a switching controller is given based on backstepping technology and stochastic small-gain theorem. In Section 6, an example is shown to illustrate the validity of the design. Finally, conclusions are drawn in Section 7.
2. Stochastic Differential Equation of Markovian Jump System
Throughout the paper, unless otherwise specified, we denote by  a complete probability space with a filtration
a complete probability space with a filtration  satisfying the usual conditions (i.e., it is right continuous, and
satisfying the usual conditions (i.e., it is right continuous, and  contains all
contains all  -null sets). Let
-null sets). Let  stand for the usual Euclidean norm for a vector
stand for the usual Euclidean norm for a vector  and
and  stand for the supremum of vector
stand for the supremum of vector  over time period
over time period  , that is,
, that is,  . The superscript
. The superscript  will denote transpose, and we refer to
will denote transpose, and we refer to  as the trace for matrix. In addition, we use
as the trace for matrix. In addition, we use  to denote the space of Lebesgue square integrable vector.
to denote the space of Lebesgue square integrable vector.
Take into account the following Markovian jump nonlinear system:

where  , and
, and  is the state vector and input vector of the system, respectively.
is the state vector and input vector of the system, respectively.  is a right-continuous Markov chain on the probability space taking values in finite state space
is a right-continuous Markov chain on the probability space taking values in finite state space  , and
, and  is
is  -dimensional independent standard Wiener process defined on the probability space, which is independent of the Markov chain
-dimensional independent standard Wiener process defined on the probability space, which is independent of the Markov chain  . The functions
. The functions  and
and  are locally Lipschitz in
are locally Lipschitz in  , for all
, for all  , namely, for any
, namely, for any  , there is a constant
, there is a constant  such that
such that

Consider the right-continuous Markov chain  , and we introduce
, and we introduce  , the indicator process for the regime
, the indicator process for the regime  , as
, as

And  satisfies the following differential equation [15]:
satisfies the following differential equation [15]:

with  , an
, an  -martingale satisfying
-martingale satisfying  , and
, and  the chain generator, an
the chain generator, an  matrix. The entries
matrix. The entries  are interpreted as transition rates such that
are interpreted as transition rates such that

where  and
and  satisfies
satisfies  . Here
. Here  is the transition rate from regime
is the transition rate from regime  to regime
to regime  . Notice that the total probability axiom imposes
. Notice that the total probability axiom imposes  negative and
negative and

Let  denote the family of all functions
denote the family of all functions  on
on  which are continuously twice differentiable in
which are continuously twice differentiable in  and once in
and once in  . Furthermore, we will give the stochastic differentiable equation of
. Furthermore, we will give the stochastic differentiable equation of  .
.
Fix any  ; by the generalized Itô formula, we have
; by the generalized Itô formula, we have

According to (2.4), the differential equation of the indicator  is as following:
is as following:

Submit (2.8) into (2.7) and notice that

There is

Therefore, the stochastic differentiable equation of  is given by the following:
is given by the following:

We take the expectation in (2.11), so that the the infinitesimal generator produces [18, 19, 23]

Remark 2.1.
The differential equation of Markovian jump system (2.1) is given as above and, the similar result is also achieved by Yuan and Mao [19]. Compared with the differential equation of general nonjump systems, two parts come forth as differences: transition rates  and the martingale process
and the martingale process  , which are both caused by the property of Markov chain
, which are both caused by the property of Markov chain  (see (2.4)). Up till now, switching controller design for jump systems contains only the transition rate
(see (2.4)). Up till now, switching controller design for jump systems contains only the transition rate  in most cases. In this paper, the controller design will take into account the martingale process as well since the jump systems considered here are of the form of lower triangular. The detailed description will be given in Section 4.
in most cases. In this paper, the controller design will take into account the martingale process as well since the jump systems considered here are of the form of lower triangular. The detailed description will be given in Section 4.
3. JISpS and Stochastic Small-Gain Theorem
Definition 3.1.
Markovian jump system (2.1) is  -moment Jump Input-to-State practically Stable (JISpS) if there exist
-moment Jump Input-to-State practically Stable (JISpS) if there exist  function
function  ,
,  function
function  , and a constant
, and a constant  such that
such that

Definition 3.2.
Markovian jump system (2.1) is JISpS in probability if for any given  there exist
there exist  function
function  ,
,  function
function  , and a constant
, and a constant  such that
such that

Remark 3.3.
The concept of Input-to-State Stability (ISS) is a well-known classical tool for designing nonlinear systems, which means for a bounded control input  , the trajectories remain in the ball of radius as
, the trajectories remain in the ball of radius as  ; furthermore, as time
; furthermore, as time  increases, all trajectories approach the smaller ball of radius
increases, all trajectories approach the smaller ball of radius  . However, for general nonlinear systems disturbed by noise and/or unmodeled dynamics, it is impossible to obtain such strong conclusion, therefore some generalized results are put forward: Noise-to-State Stability (NSS) [31] and Input-to-State practically Stable (ISpS) [32]. In the definition of ISpS, the trajectories remain in the ball of radius as
. However, for general nonlinear systems disturbed by noise and/or unmodeled dynamics, it is impossible to obtain such strong conclusion, therefore some generalized results are put forward: Noise-to-State Stability (NSS) [31] and Input-to-State practically Stable (ISpS) [32]. In the definition of ISpS, the trajectories remain in the ball of radius as  instead of
instead of  . Similar to ISS, as time
. Similar to ISS, as time  increases, all trajectories approach the smaller ball of radius
increases, all trajectories approach the smaller ball of radius  , and the system is still BIBO. As can be seen in the following analysis of this paper, bound
, and the system is still BIBO. As can be seen in the following analysis of this paper, bound  can be made as small as possible by choosing appropriate control parameters. For some special cases, if
can be made as small as possible by choosing appropriate control parameters. For some special cases, if  , the ISpS is reduced to ISS.
, the ISpS is reduced to ISS.
Remark 3.4.
The definition of Input-to-State practically Stable (ISpS) in probability for nonjump stochastic system is put forward by Wu et al. [32], and the difference between JISpS in probability and ISpS in probability lies in the expressions of system state  and control signal
and control signal  . For nonjump system, system state and control signal contain only continuous time
. For nonjump system, system state and control signal contain only continuous time  with
with  , while for jump system, they concern with both continuous time
, while for jump system, they concern with both continuous time  and discrete regime
and discrete regime  . For different system dynamic
. For different system dynamic  , control signal
, control signal  will differ even with the same time
will differ even with the same time  taken and that is the reason why it is called a switching controller. Based on the idea of switching control, the corresponding stability is called " Jump ISpS" and it is a more general extension of ISpS. By choosing
taken and that is the reason why it is called a switching controller. Based on the idea of switching control, the corresponding stability is called " Jump ISpS" and it is a more general extension of ISpS. By choosing  , the definition of JISpS will degenerate to ISpS.
, the definition of JISpS will degenerate to ISpS.
Remark 3.5.
This paper introduces two kinds of JISpS in the sense of stochastic stability:  -moment JISpS and JISpS in probability. According to the knowledge of stochastic process, if one system is
-moment JISpS and JISpS in probability. According to the knowledge of stochastic process, if one system is  -moment stochastically stable, it must be stochastically stable in probability by using martingale inequality. Here only sufficient conditions for
-moment stochastically stable, it must be stochastically stable in probability by using martingale inequality. Here only sufficient conditions for  -moment stochastic stability are considered and now introduce the following stochastic Lyapunov stability criterion.
-moment stochastic stability are considered and now introduce the following stochastic Lyapunov stability criterion.
Theorem 3.6.
For Markovian jump system (2.1), let  be positive numbers. Assume that there exist a function
be positive numbers. Assume that there exist a function  , a
, a  function
function  , and constants
, and constants  , satisfying
, satisfying


for all  , then jump system (2.1) is pth moment JISpS and JISpS in probability as well.
, then jump system (2.1) is pth moment JISpS and JISpS in probability as well.
Proof.
Clearly the conclusion holds if  . So we only need proof for
. So we only need proof for  . Fix such
. Fix such  arbitrarily, we write
arbitrarily, we write  as
as  .
.
For each integer  , define a stopping time as
, define a stopping time as

Obviously,  almost surely as
almost surely as  . Noticing that
. Noticing that  if
if  , we can apply the generalized Itô formula to derive that for any
, we can apply the generalized Itô formula to derive that for any 

Let  , apply Fatou's lemma to (3.6), and we have
, apply Fatou's lemma to (3.6), and we have

According to Mean value theorems for integration, there is

Noticing the property of  function, the following inequality is deduced:
function, the following inequality is deduced:

Submitting (3.3) into (3.9) gives

Consequently,

In (3.11), define  function
function  ,
,  function
function  , and positive constant
, and positive constant  as:
as:

There is

This completes the proof.
Consider the jump interconnected dynamic system described in Figure 1:

where  is the state of system, and
is the state of system, and  denotes exterior disturbance and/or interior uncertainty.
denotes exterior disturbance and/or interior uncertainty.  is independent Wiener noise with appropriate dimension, and we introduce the following stochastic nonlinear small-gain theorem as a lemma, which is an extension of the corresponding result in Wu et al. [32].
is independent Wiener noise with appropriate dimension, and we introduce the following stochastic nonlinear small-gain theorem as a lemma, which is an extension of the corresponding result in Wu et al. [32].
Lemma 3.7 (Stochastic small-gain theorem).
Suppose that both the  -system and
-system and  -system are JISpS in probability with
-system are JISpS in probability with  as input and
as input and  as state, and
as state, and  as input and
as input and  as state, respectively, that is, for any given
as state, respectively, that is, for any given  ,
,

hold with  being
being  function,
function,  and
and  being
being  functions, and
functions, and  being nonnegative constants,
being nonnegative constants,  . If there exist nonnegative parameters
. If there exist nonnegative parameters  such that nonlinear gain functions
such that nonlinear gain functions  satisfy
satisfy

the interconnected system is JISpS in probability with  as input and
as input and  as state, that is, for any given
as state, that is, for any given  , there exist a
, there exist a  function
function  , a
, a  function
function  , and a parameter
, and a parameter  such that
such that

Remark 3.8.
Small-gain theorem for nonlinear systems was firstly provided by Mareels and Hill [33] and was extended to the stochastic case by Wu et al. [32]. The above stochastic small-gain theorem for jump systems is an extension of the nonjump case. This extension can be achieved without any mathematical difficulties, and the proof process is the same as in [32]. The reason is that in Lemma 3.7 we only take into account the interconnection relationships between interconnected system and its subsystems, despite subsystems are of jump or nonjump case. If both subsystems are nonjump and ISpS in probability, respectively, the interconnected system is ISpS in probability. In contrast, if both subsystems are jump and JISpS in probability, respectively, the interconnected system is JISpS in probability and so on.
4. Problem Description
Consider the following Markovian jump nonlinear systems with unmodeled dynamics described by

where  is system state vector,
is system state vector,  is system input signal,
is system input signal,  is unmeasured state vector, and
is unmeasured state vector, and  is output signal. The Markov chain
is output signal. The Markov chain  is as defined in Section 2.
is as defined in Section 2.  is a smooth function, and
is a smooth function, and  denotes the unmodeled dynamic uncertainty which could be different with different system regime
denotes the unmodeled dynamic uncertainty which could be different with different system regime  . Both
. Both  and
and  are locally Lipschitz as described in Section 2.
are locally Lipschitz as described in Section 2.
Our design purpose is to find a switching controller  of the form
of the form  , such that the closed-loop jump system could be JISpS in probability, and the system output
, such that the closed-loop jump system could be JISpS in probability, and the system output  could be within an attractive region around the equilibrium point with radius as small as possible. In this paper, the following assumptions are made for jump system (4.1):
could be within an attractive region around the equilibrium point with radius as small as possible. In this paper, the following assumptions are made for jump system (4.1):
(A1)The  subsystem with input
subsystem with input  is JISpS in probability, namely, there exists a smooth positive definite Lyapunov function
is JISpS in probability, namely, there exists a smooth positive definite Lyapunov function  such that
such that

where  is
is  function,
function,  is positive integer, and
is positive integer, and  are constants.
are constants.
(A2)For each  ,
,  , there exists an unknown positive constant
, there exists an unknown positive constant  such that
such that

where  is known constant and
is known constant and  are known nonnegative smooth functions for any given
are known nonnegative smooth functions for any given  .
.
For the design of switching controller, we introduce the following lemmas.
Lemma 4.1 (Young's inequality).
For any two vectors  , the following inequality holds
, the following inequality holds

where  and the constants
and the constants  satisfy
satisfy  .
.
Lemma 4.2 (Martingale representation [34]).
Let  be N-dimensional standard Wiener noise. Suppose
be N-dimensional standard Wiener noise. Suppose  is an
is an  -martingale (w.r.t. P) and that
-martingale (w.r.t. P) and that  , for all
, for all  , then there exists a stochastic process
, then there exists a stochastic process  , such that
, such that

5. Controller Design and Stability Analysis
Now we seek the switching controller  for jump system (4.1) so that the closed-loop system could be JISpS in probability. Perform a new transformation as
for jump system (4.1) so that the closed-loop system could be JISpS in probability. Perform a new transformation as

For simplicity, we just denote  ,
,  by
by  ,
,  ,
,  ,
,  , where
, where  , and the new coordinate is
, and the new coordinate is  .
.
According to stochastic differential equation (2.11), one has:

Here we define

From assumption (A2), one gets that there exist nonnegative smooth functions  ,
,  satisfying
satisfying

The inequality (5.4) could easily be deduced by using Lemma 4.1.
Now we turn to the martingale process  ; according to Lemma 4.2, there exist a function
; according to Lemma 4.2, there exist a function  and an
and an  -dimensional standard Wiener noise
-dimensional standard Wiener noise  satisfying
satisfying  , where
, where  , and
, and  is a positive bounded constant. Therefore we have
is a positive bounded constant. Therefore we have

Remark 5.1.
Differential equation of new coordinate  is deduced as above. The martingale process resulting from Markov process is transformed into Wiener noise by using Martingale representation theorem, and it will affect the Lyapunov function construction and affect the remainder of the control design process; for nonjump systems with uncertainty, a quadratic Lyapunov is chosen to meet control performance in most cases [32, 35, 36]. However, for jump systems, this choice will fail because of the existence of martingale process (or Wiener noise). To solve this problem, we suggest using quartic Lyapunov function instead of quadratic one, and this will increase largely the difficulty of design.
is deduced as above. The martingale process resulting from Markov process is transformed into Wiener noise by using Martingale representation theorem, and it will affect the Lyapunov function construction and affect the remainder of the control design process; for nonjump systems with uncertainty, a quadratic Lyapunov is chosen to meet control performance in most cases [32, 35, 36]. However, for jump systems, this choice will fail because of the existence of martingale process (or Wiener noise). To solve this problem, we suggest using quartic Lyapunov function instead of quadratic one, and this will increase largely the difficulty of design.
Choose the quartic Lyapunov function as

In the view of (5.5) and (5.6), the infinitesimal generator of  satisfies
satisfies

The following inequalities could be deduced by using Young's inequality and norm inequalities with the help of changing the order of summations or exchanging the indices of the summations:

where  , and
, and  are design parameters.
are design parameters.
Based on assumption (A2) and (5.4), we obtain the following inequality by applying Lemma 4.1:

Here  ,
,  are design parameters.
are design parameters.
Submit (5.9) into (5.7), there is

Choose the virtual control signal as

Thus the real control signal  is
is  such that
such that

where  ,
,  , and
, and  function
function  is chosen to satisfy
is chosen to satisfy  .
.
Theorem 5.2.
If Assumptions (A1) and (A2) hold and a switching control law (5.11) is adopted, the interconnected Markovian jump system (4.1) is JISpS in probability, and all solutions of closed-loop system are ultimately bounded. Furthermore, the system output could be regulated to a small neighborhood of the equilibrium point with preset precision in probability within finite time.
Proof.
From Assumption (A1), the  subsystem is JISpS in probability. There exist
subsystem is JISpS in probability. There exist  such that
such that

Considering (5.12), for any given  , there is
, there is

Notice the fact that  stands up as long as
stands up as long as  and vice versa. Thus we have
and vice versa. Thus we have

In (5.15), appropriate parameter  can be chosen to satisfy
can be chosen to satisfy  .
.
According to Theorem 3.6 and (5.12), with switching controller  adopted, the
adopted, the  subsystem of jump system (4.1) is JISpS in probability with
subsystem of jump system (4.1) is JISpS in probability with  as system state and
as system state and  as input, which means for any given
as input, which means for any given  , there exists
, there exists  function
function  ,
,  function
function  , and
, and  such that
such that

On the other hand, according to Assumption (A1), there is

Similarly, by choosing parameter  , for any given
, for any given  , there exist
, there exist  function
function  ,
,  function
function  , and
, and  such that
such that

Here parameter  can be chosen to satisfy
can be chosen to satisfy  .
.
By combining (5.16) and (5.18) we choose parameters  guaranteeing that
guaranteeing that

According to stochastic small-gain theorem, for any given  , there exists
, there exists  function
function  such that
such that

where  ,
,  is given as in [32]. From (5.20) it can be seen that all solutions of closed-loop system are ultimately bounded in probability.
is given as in [32]. From (5.20) it can be seen that all solutions of closed-loop system are ultimately bounded in probability.
According to (5.20) and the property of  function, for any given
function, for any given  , there exists
, there exists  . If
. If  , there is
, there is  . At the same time by choosing approximate parameter, it can be guaranteed that
. At the same time by choosing approximate parameter, it can be guaranteed that  .
.
Let  , thus we have that for any given
, thus we have that for any given  , there exists
, there exists  and
and  such that if
such that if  , the output of jump system
, the output of jump system  satisfies
satisfies

meanwhile  can be made as small as possible by choosing approximate parameters
can be made as small as possible by choosing approximate parameters  . The proof is completed.
. The proof is completed.
Remark 5.3.
Theorem 5.2 shows that if both  subsystem and
subsystem and  subsystem are JISpS in probability, the jump system (4.1) is JISpS in probability with appropriate control parameters chosen. Meanwhile the system output can be regulated to a small region in probability with preset precision within finite time. In the following simulation, we will show how different parameters affect the system states and output.
subsystem are JISpS in probability, the jump system (4.1) is JISpS in probability with appropriate control parameters chosen. Meanwhile the system output can be regulated to a small region in probability with preset precision within finite time. In the following simulation, we will show how different parameters affect the system states and output.
6. Simulation
Consider a two-order Markovian jump nonlinear system with regime transition space  , and the transition rate matrix is
, and the transition rate matrix is  .
.
The system with unmodeled dynamics is as follows:

Here

From Assumption (A2), we have

where  ,
,  , and the
, and the  subsystem satisfies
subsystem satisfies

where  ,
,  ,
,  . Thus the control law is taken as follows (here
. Thus the control law is taken as follows (here  ).
).
Case 1.
The system regime is  :
:

Case 2.
The system regime is  :
:

In computation, we set the initial value to be  ,
,  and the time step to be 0.05 second. For comparison, two groups of different control parameters are given. First, we take the parameter with values
and the time step to be 0.05 second. For comparison, two groups of different control parameters are given. First, we take the parameter with values  ,
,  ,
,  , and the simulation results are as follows. Figure 2 shows the regime transition of the jump system, and Figure 3 shows the corresponding switching controller
, and the simulation results are as follows. Figure 2 shows the regime transition of the jump system, and Figure 3 shows the corresponding switching controller  . Figure 4 shows the system output
. Figure 4 shows the system output  which is defined as the system state
which is defined as the system state  , and Figure 5 shows system state
, and Figure 5 shows system state  .
.
Now we choose different control parameters as  ,
,  ,
,  and repeat the simulation. The simulation results are as follows. Figure 6 shows the regime transition of the jump system, and Figure 7 shows the corresponding switching controller
and repeat the simulation. The simulation results are as follows. Figure 6 shows the regime transition of the jump system, and Figure 7 shows the corresponding switching controller  . Figure 8 shows the system output
. Figure 8 shows the system output  which is defined as the system state
which is defined as the system state  , and Figure 9 shows system state
, and Figure 9 shows system state  .
.
Comparing the results from two simulations, all the signals of closed-loop system are globally uniformly ultimately bounded, and the system output can be regulated to a neighborhood near the equilibrium point despite of different experiment samples. As can be seen from the figures, larger values of  help to increase the convergence speed of system states while larger value of
help to increase the convergence speed of system states while larger value of  and smaller values of
and smaller values of  help to increase the precision. If one wants the system states to converge to the neighborhood of the equilibrium point with fast speed and an acceptable precision, one should increase the value of
help to increase the precision. If one wants the system states to converge to the neighborhood of the equilibrium point with fast speed and an acceptable precision, one should increase the value of  and decrease
and decrease  though this choice will increase the cost of control signals.
though this choice will increase the cost of control signals.
Remark 6.1.
Much research work has been performed toward the study of nonlinear system by using small-gain theorem [4, 32, 33]. In contrast to their contributions, this paper focuses on the switching controller design for Markovian jump nonlinear system which is a more general form of nonjump systems. For each different regime  , the actual controller
, the actual controller  is different, and it consists of two parts with obvious difference (see (5.11)): the coupling of regime
is different, and it consists of two parts with obvious difference (see (5.11)): the coupling of regime  and
and  , which are both caused by the Markovian jumps (see (2.4)). By defining regime
, which are both caused by the Markovian jumps (see (2.4)). By defining regime  , the above two terms will reduce to zero. Thus this switching controller design is capable of stabilizing the general nonjump system as well.
, the above two terms will reduce to zero. Thus this switching controller design is capable of stabilizing the general nonjump system as well.
7. Conclusion
In this paper, the authors take into account switching controller design for a class of Markovian jump nonlinear system with unmodeled dynamics. Based on the differential equation and infinitesimal generator of jump systems, the concept of Jump Input-to-State Stability (JISpS) and stochastic Lyapunov stability criterion are put forward. Moreover, the martingale process caused by the stochastic Markovian jumps is converted into Wiener noise. By using backstepping technology and stochastic small-gain theorem, a switching controller is proposed which ensures JISpS in probability of the jump nonlinear system. And system output can be regulated in probability to a small neighborhood of the equilibrium point with preset precision. The result presented in this paper also stands for the general nonjump system.
References
Sontag ED: Smooth stabilization implies coprime factorization. IEEE Transactions on Automatic Control 1989,34(4):435-443. 10.1109/9.28018
Khalil HK: Nonlinear Systems. 2nd edition. Prentice-Hall, Englewood Cliffs, NJ, USA; 1996.
Kokotović PV, Arcak M: Constructive nonlinear control: a historical perspective. Automatica 2001,37(5):637-662.
Jiang Z-P: A combined backstepping and small-gain approach to adaptive output feedback control. Automatica 1999,35(6):1131-1139. 10.1016/S0005-1098(99)00015-1
Jiang Z-P, Mareels I, Hill D: Robust control of uncertain nonlinear systems via measurement feedback. IEEE Transactions on Automatic Control 1999,44(4):807-812. 10.1109/9.754823
Krstić M, Kanellakopoulos I, Kokotović PV: Nonlinear and Adaptive Control Design. John Wiley & Sons, New York, NY, USA; 1995.
Seto D, Annaswamy AM, Baillieul J: Adaptive control of nonlinear systems with a triangular structure. IEEE Transactions on Automatic Control 1994,39(7):1411-1428. 10.1109/9.299624
Čelikovský S, Nijmeijer H: Equivalence of nonlinear systems to triangular form: the singular case. Systems & Control Letters 1996,27(3):135-144. 10.1016/0167-6911(95)00059-3
Chen H, Ji H-B, Wang B, Xi H-S: Coordinated passivation techniques for the dual-excited and steam-valving control of synchronous generators. IEE Proceedings: Control Theory and Applications 2006,153(1):69-73. 10.1049/ip-cta:20045016
Jiang Z-P, Nijmeijer H: Tracking control of mobile robots: a case study in backstepping. Automatica 1997,33(7):1393-1399. 10.1016/S0005-1098(97)00055-1
Do KD, Jiang ZP, Pan J: On global tracking control of a VTOL aircraft without velocity measurements. IEEE Transactions on Automatic Control 2003,48(12):2212-2217. 10.1109/TAC.2003.820148
Chang Y-C, Yen H-M: Adaptive output feedback tracking control for a class of uncertain nonlinear systems using neural networks. IEEE Transactions on Systems, Man, and Cybernetics, Part B 2005,35(6):1311-1316. 10.1109/TSMCB.2005.850158
Cai Z, de Queiroz MS, Dawson DM: Robust adaptive asymptotic tracking of nonlinear systems with additive disturbance. IEEE Transactions on Automatic Control 2006,51(3):524-529. 10.1109/TAC.2005.864204
Kac IYa, Krasovskii NN: About stability of systems with stochastic parameters. Prikladnaya Matematika i Makhanika 1960,24(5):809-823.
Mariton M: Jump Linear Systems in Automatic Control. Marcel-Dekker, New York, NY, USA; 1990.
Kac IYa: Method of Lyapunov functions in problems of stability and stabilization of systems of stochastic structure. Ekaterinburg, Russia, 1998
Shaikhet L: Stability of stochastic hereditary systems with Markovian switching. Theory of Stochastic Process 1996,2(18):180-184.
Mao X: Stability of stochastic differential equations with Markovian switching. Stochastic Processes and Their Applications 1999,79(1):45-67. 10.1016/S0304-4149(98)00070-2
Yuan C, Mao X: Asymptotic stability in distribution of stochastic differential equations with Markovian switching. Stochastic Processes and Their Applications 2003,103(2):277-291. 10.1016/S0304-4149(02)00230-2
Mao X, Shaikhet L: Delay-dependent stability criteria for stochastic differential delay equations with Markovian switching. Stability and Control: Theory and Applications 2000,3(2):88-102.
Mao X: Robustness of stability of stochastic differential delay equations with Markovian switching. Stability and Control: Theory and Applications 2000,3(1):48-61.
Mao X: Asymptotic stability for stochastic differential delay equations with Markovian switching. Functional Differential Equations 2002,9(1-2):201-220.
Yuan C, Mao X: Robust stability and controllability of stochastic differential delay equations with Markovian switching. Automatica 2004,40(3):343-354. 10.1016/j.automatica.2003.10.012
de Souza CE, Trofino A, Barbosa KA:Mode-independent
 filters for Markovian jump linear systems. IEEE Transactions on Automatic Control 2006,51(11):1837-1841.
filters for Markovian jump linear systems. IEEE Transactions on Automatic Control 2006,51(11):1837-1841.Zhu J, Park J, Lee K-S, Spiryagin M: Robust extended Kalman filter of discrete-time Markovian jump nonlinear system under uncertain noise. Journal of Mechanical Science and Technology 2008,22(6):1132-1139. 10.1007/s12206-007-1048-z
Nguang SK, Shi P:Robust
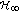 output feedback control design for Takagi-Sugeno systems with Markovian jumps: a linear matrix inequality approach. Journal of Dynamic Systems, Measurement and Control 2006,128(3):617-625. 10.1115/1.2232686
output feedback control design for Takagi-Sugeno systems with Markovian jumps: a linear matrix inequality approach. Journal of Dynamic Systems, Measurement and Control 2006,128(3):617-625. 10.1115/1.2232686Zhu J, Xi H-S, Ji H-B, Wang B: Robust adaptive tracking for Markovian jump nonlinear systems with unknown nonlinearities. Discrete Dynamics in Nature and Society 2006, 2006:-18.
Jin Z, Hongsheng X, Xiaobo X, Haibo J: Guaranteed control performance robust LQG regulator for discrete-time Markovian jump systems with uncertain noise. Journal of Systems Engineering and Electronics 2007,18(4):885-891. 10.1016/S1004-4132(08)60036-5
Chen C, Li H-X, Dong D: Hybrid control for robot navigation: a hierarchical Q-learning algorithm. IEEE Robotics and Automation Magazine 2008,15(2):37-47.
Dong D, Chen C, Li H, Tarn T-J: Quantum reinforcement learning. IEEE Transactions on Systems, Man, and Cybernetics, Part B 2008,38(5):1207-1220.
Deng H, Krstić M, Williams RJ: Stabilization of stochastic nonlinear systems driven by noise of unknown covariance. IEEE Transactions on Automatic Control 2001,46(8):1237-1253. 10.1109/9.940927
Wu Z-J, Xie X-J, Zhang S-Y: Adaptive backstepping controller design using stochastic small-gain theorem. Automatica 2007,43(4):608-620. 10.1016/j.automatica.2006.10.020
Mareels IMY, Hill DJ: Monotone stability of nonlinear feedback systems. Journal of Mathematical Systems, Estimation, and Control 1992,2(3):275-291.
Øksendal B: Stochastic Differential Equations. Springer, New York, NY, USA; 2000.
Polycarpou MM, Ioannou PA: A robust adaptive nonlinear control design. Automatica 1996,32(3):423-427. 10.1016/0005-1098(95)00147-6
Wang B, Ji H, Zhu J, Xiao X: Robust adaptive control of polynomial lower-triangular systems with dynamic uncertainties. Proceedings of the 6th World Congress on Intelligent Control and Automation (WCICA '06), June 2006, Dalian, China 1: 815-819.
Acknowledgment
This work has been funded by BK21 research project: Switching Control of Systems with Structure Uncertainty and Noise.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhu, J., Park, J., Lee, KS. et al. Switching Controller Design for a Class of Markovian Jump Nonlinear Systems Using Stochastic Small-Gain Theorem. Adv Differ Equ 2009, 896218 (2009). https://doi.org/10.1155/2009/896218
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/896218


 .
.

 .
.

 .
.

 .
.

 .
.

 .
.

 .
.

 .
.
 filters for Markovian jump linear systems. IEEE Transactions on Automatic Control 2006,51(11):1837-1841.
filters for Markovian jump linear systems. IEEE Transactions on Automatic Control 2006,51(11):1837-1841.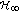 output feedback control design for Takagi-Sugeno systems with Markovian jumps: a linear matrix inequality approach. Journal of Dynamic Systems, Measurement and Control 2006,128(3):617-625. 10.1115/1.2232686
output feedback control design for Takagi-Sugeno systems with Markovian jumps: a linear matrix inequality approach. Journal of Dynamic Systems, Measurement and Control 2006,128(3):617-625. 10.1115/1.2232686