- Research Article
- Open access
- Published:
Construction of the General Solution of Planar Linear Discrete Systems with Constant Coefficients and Weak Delay
Advances in Difference Equations volume 2009, Article number: 784935 (2009)
Abstract
Planar linear discrete systems with constant coefficients and weak delay are considered. The characteristic equations of such systems are identical with those for the same systems but without delayed terms. In this case, the space of solutions with a given starting dimension is pasted after several steps into a space with dimension less than the starting one. In a sense this situation copies an analogous one known from the theory of linear differential systems with constant coefficients and weak delay when the initially infinite dimensional space of solutions on the initial interval on a reduced interval, turns (after several steps) into a finite dimensional set of solutions. For every possible case, general solutions are constructed and, finally, results on the dimensionality of the space of solutions are deduced.
1. Introduction
1.1. Preliminary Notions and Properties
We use the following notation: for integers  ,
,  ,
,  , we define
, we define  where
where  or
or  are admitted, too. Throughout this paper, using notation
are admitted, too. Throughout this paper, using notation  , we always assume
, we always assume  . In this paper we deal with the discrete planar systems
. In this paper we deal with the discrete planar systems

where  is a fixed integer,
is a fixed integer,  ,
,  and
and  are constant
are constant  matrices, and
matrices, and  . Following the terminology (used, e.g., in [1, 2]), (1.1) is referred to as a nondelayed discrete system if
. Following the terminology (used, e.g., in [1, 2]), (1.1) is referred to as a nondelayed discrete system if  and as a delayed discrete system if
and as a delayed discrete system if  . Together with (1.1), we consider an initial (Cauchy) problem
. Together with (1.1), we consider an initial (Cauchy) problem

where  with
with  . We will investigate only the case
. We will investigate only the case  since the solution of (1.1) for
since the solution of (1.1) for  is given by the known formula
is given by the known formula  for
for  .
.
The existence and uniqueness of the solution of the initial problems (1.1) and (1.2) on  are obvious. We recall that the solution
are obvious. We recall that the solution of (1.1) and (1.2) is defined as an infinite sequence
of (1.1) and (1.2) is defined as an infinite sequence

such that, for any  , equality (1.1) holds.
, equality (1.1) holds.
The space of all initial data (1.2) with  is obviously
is obviously  -dimensional. Below we describe the fact that, among the systems (1.1), there are such systems that their space of solutions, being initially
-dimensional. Below we describe the fact that, among the systems (1.1), there are such systems that their space of solutions, being initially  -dimensional, on a reduced interval turns into a space having dimension less than
-dimensional, on a reduced interval turns into a space having dimension less than  .
.
1.2. Systems with Weak Delay
We consider the system (1.1) and we look for a solution having the form  ,
,  ,
,  with a
with a  . The usual procedure leads to a characteristic equation
. The usual procedure leads to a characteristic equation

where  is the unit
is the unit  matrix. Together with (1.1), we consider a system with the terms containing delays omitted
matrix. Together with (1.1), we consider a system with the terms containing delays omitted

and the characteristic equation

Definition 1.1.
The system (1.1) is called a system with weak delay if the characteristic equations (1.4) and (1.6) corresponding to systems (1.1) and (1.5) are equal, that is, if for every 

We consider a linear transformation

with a nonsingular  matrix
matrix  . Then the discrete system for
. Then the discrete system for  is
is

with  ,
,  . We show that the property of a system to be the system with weak delay is preserved by every nonsingular linear transformation.
. We show that the property of a system to be the system with weak delay is preserved by every nonsingular linear transformation.
Lemma 1.2.
If the system (1.1) is a system with weak delay, then its arbitrary linear nonsingular transformation (1.8) again leads to a system with the weak delay (1.9).
Proof.
It is easy to show that

holds since

and the equality

is assumed.
1.3. Necessary and Sufficient Conditions Determining the Weak Delay
In the forthcoming theorem, we give conditions, in terms of determinants, indicating whether a system is a system with weak delay or not.
Theorem 1.3.
System (1.1) is a system with weak delay if and only if the following three conditions hold simultaneously:

Proof.
We start with computing the determinant (1.4). We get

Now we see that, for (1.7) to hold, that is,

conditions (1.13) are both necessary and sufficient.
Remark 1.4.
It is easy to see that conditions (1.13) are equivalent to

1.4. Problem under Consideration
The aim of this paper is to show that the dimension of the space of all solutions, being initially equal to the dimension  of the space of initial data (1.2) generated by discrete functions
of the space of initial data (1.2) generated by discrete functions  , is, after several steps, reduced (on an interval of the form
, is, after several steps, reduced (on an interval of the form  with an
with an  ) to a dimension less than the initial one. In other words, we will show that the
) to a dimension less than the initial one. In other words, we will show that the  -dimensional space of all solutions of (1.1) is reduced to a less-dimensional space of solutions on
-dimensional space of all solutions of (1.1) is reduced to a less-dimensional space of solutions on  . This problem is solved directly by explicitly computing the corresponding solutions of the Cauchy problems with each of the cases arising being considered. The underlying idea for such investigation is simple. If (1.1) is a system with weak delay, then the corresponding characteristic equation has only two eigenvalues instead of
. This problem is solved directly by explicitly computing the corresponding solutions of the Cauchy problems with each of the cases arising being considered. The underlying idea for such investigation is simple. If (1.1) is a system with weak delay, then the corresponding characteristic equation has only two eigenvalues instead of  eigenvalues in the case of systems with nonweak delay. This explains why the dimension of the space of solutions becomes less than the initial one. The final results (Theorems 2.5–2.8) provide the dimension of the space of solutions.
eigenvalues in the case of systems with nonweak delay. This explains why the dimension of the space of solutions becomes less than the initial one. The final results (Theorems 2.5–2.8) provide the dimension of the space of solutions.
1.5. Auxiliary Formula
For the reader's convenience we recall one explicit formula (see, e.g., [3]) for the solutions of linear scalar discrete nondelayed equations used in this paper. We consider the first-order linear discrete nonhomogeneous equation

with  and
and  . Then it is easy to verify that
. Then it is easy to verify that

Throughout the paper, we adopt the customary notation for the sum:  where
where  is an integer,
is an integer,  is a positive integer and, "
is a positive integer and, " " denotes the function considered independently of whether it is defined for indicated arguments or not.
" denotes the function considered independently of whether it is defined for indicated arguments or not.
2. Results
If (1.7) holds, then (1.4) and (1.6) have only two (and the same) roots simultaneously. In order to prove the properties of the family of solutions of (1.1) formulated in Section 1.4, we will separately discuss all the possible combinations of roots, that is, the cases of two real and distinct roots, a couple of complex conjugate roots, and, finally, a two-fold real root.
2.1. Jordan Forms of Matrix 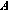 and Corresponding Solutions of The Problem (1.1), (1.2)
and Corresponding Solutions of The Problem (1.1), (1.2)
It is known that, for every matrix  , there exists a nonsingular matrix
, there exists a nonsingular matrix  transforming it to the corresponding Jordan matrix form
transforming it to the corresponding Jordan matrix form  . This means that
. This means that

where  has the following possible forms, depending on the roots of the characteristic equation (1.6), that is, on the roots of
has the following possible forms, depending on the roots of the characteristic equation (1.6), that is, on the roots of

If (2.2) has two real distinct roots  ,
,  , then
, then

if the roots are complex conjugate, that is,  with
with  , then
, then

and, finally, in the case of one two-fold real root  , we have either
, we have either

or

The transformation  transforms (1.1) into a system
transforms (1.1) into a system

with  ,
,  ,
,  . Together with (2.7), we consider an initial problem
. Together with (2.7), we consider an initial problem

 with
with  where
where  is the initial function corresponding to the initial function
is the initial function corresponding to the initial function  in (1.2).
in (1.2).
Below we consider all four possible cases (2.3)–(2.6) separately.
We define

Assuming that the system (1.1) is a system with weak delay, the system (2.7), due to Lemma 1.2, is a system with weak delay again.
2.1.1. The Case (2.3) of Two Real Distinct Roots
In this case, we have  . The necessary and sufficient conditions (1.13) for (2.7) turn into
. The necessary and sufficient conditions (1.13) for (2.7) turn into



Since  , (2.10), (2.12) yield
, (2.10), (2.12) yield  . Then, from (2.11), we get
. Then, from (2.11), we get  , so either
, so either  or
or  .
.
Theorem 2.1.
Let (1.1) be a system with weak delay and (2.2) admit two real distinct roots  ,
,  . Then
. Then  . The solution of the initial problems (1.1) and (1.2) is
. The solution of the initial problems (1.1) and (1.2) is  ,
,  where
where  has, in the case
has, in the case  , the form
, the form

and, in the case  , the form
, the form

Proof.
In the case considered we have  and the transformed system (2.7) takes either the form
and the transformed system (2.7) takes either the form


if  or the form
or the form


if  . We investigate only the initial problem (2.15), (2.16), (2.8) since the initial problem (2.17), (2.18), (2.8) can be examined in a similar way. From (2.16) and (2.8), we get
. We investigate only the initial problem (2.15), (2.16), (2.8) since the initial problem (2.17), (2.18), (2.8) can be examined in a similar way. From (2.16) and (2.8), we get

Then (2.15) becomes

First we solve this equation for  . This means that we consider the problem
. This means that we consider the problem

With the aid of formula (1.18), we get

Now we solve (2.20) for  , that is, we consider the problem (with initial data deduced from (2.22)
, that is, we consider the problem (with initial data deduced from (2.22)

Applying formula (1.18) yields (for  )
)

Picking up all particular cases (2.8), (2.22), and (2.24), we have

Now, taking into account (2.9), the formula (2.13) is a consequence of (2.19) and (2.25). The formula (2.14) can be proved in a similar way.
Finally, we note that both formulas (2.13) and (2.14) remain valid for  as well. In this case, the transformed system (2.7) reduces to a system without delay.
as well. In this case, the transformed system (2.7) reduces to a system without delay.
2.1.2. The Case (2.4) of Two Complex Conjugate Roots
The necessary and sufficient conditions (1.13) for (2.7) take the forms (2.10) and (2.11) and

The system of conditions (2.10), (2.11), and (2.26) gives  ,
,  and admits only one possibility, namely,
and admits only one possibility, namely,

Consequently,  and
and  as well. The initial problems (1.1) and (1.2) reduces to a problem without delay
as well. The initial problems (1.1) and (1.2) reduces to a problem without delay

and, obviously,

2.1.3. The Case (2.5) of Two-Fold Real Root
We have  . The necessary and sufficient conditions (1.13) are, for (2.7), reduced to (2.10), (2.11), and
. The necessary and sufficient conditions (1.13) are, for (2.7), reduced to (2.10), (2.11), and

From (2.10), (2.11), and (2.30), we get  . Now we will analyse the two possible cases:
. Now we will analyse the two possible cases:  and
and  .
.
The Case 

Theorem 2.2.
Let (1.1) be a system with weak delay, (2.2) admit a two-fold root  ,
,  and the matrix
and the matrix  has the form (2.5). Then the solution of the initial problems (1.1) and (1.2) is
has the form (2.5). Then the solution of the initial problems (1.1) and (1.2) is  ,
,  where
where  has, in the case
has, in the case  , the form
, the form

and, in the case  , the form
, the form

Proof.
The assumption  or
or  leads to
leads to  . Then the following cases arise. Either
. Then the following cases arise. Either  ,
,  or
or  ,
,  or
or  . The latter case is covered by the above formulas (2.31) and (2.32) since it can be treated as system (2.28) considered previously (with
. The latter case is covered by the above formulas (2.31) and (2.32) since it can be treated as system (2.28) considered previously (with  ) when
) when  , and the corresponding solution is described by the formula (2.29). If
, and the corresponding solution is described by the formula (2.29). If  , then (2.7) turns into the system
, then (2.7) turns into the system

and, if  , then (2.7) turns into the system
, then (2.7) turns into the system

System (2.33) can be solved in much the same way as the systems (2.15) and (2.16) if we put  , and the discussion of the system (2.34) copies the discussion of the systems (2.17) and (2.18) with
, and the discussion of the system (2.34) copies the discussion of the systems (2.17) and (2.18) with  . Formulas (2.31) and (2.32) are consequences of (2.13) and (2.14).
. Formulas (2.31) and (2.32) are consequences of (2.13) and (2.14).
The Case 
For  we define
we define

Theorem 2.3.
Let the system (1.1) be a system with weak delay, (2.2) admit two repeated roots  ,
,  , and the matrix
, and the matrix  has the form (2.5). Then the solution of the initial problems (1.1) and (1.2) is given by
has the form (2.5). Then the solution of the initial problems (1.1) and (1.2) is given by  ,
,  where
where  has the form
has the form

Proof.
In this case, all the entries of  are nonzero and, from (2.10), (2.11), and (2.30), we get
are nonzero and, from (2.10), (2.11), and (2.30), we get

Then the system (2.7) reduces to


where  . It is easy to see (multiplying (2.39) by
. It is easy to see (multiplying (2.39) by  and summing both equations) that
and summing both equations) that

We can see (2.40) as a homogeneous equation with respect to the unknown expression  . Then, using (1.18), we obtain
. Then, using (1.18), we obtain

With the aid of (2.41), we rewrite the systems (2.38) and (2.39) as follows:

It is easy to see that the system (2.42) is decomposed into two separate equations. Solving each of them in a similar way as in the proof of Theorem 2.1 using (1.18) (details are omitted), we conclude

Formula (2.36) is now a direct consequence of (2.43) and (2.35).
2.1.4. The Case (2.6) of Two-Fold Real Root
If the matrix  has the form (2.6), the necessary and sufficient conditions (1.13), for (2.7), are reduced to (2.10), (2.11), and
has the form (2.6), the necessary and sufficient conditions (1.13), for (2.7), are reduced to (2.10), (2.11), and

Then (2.10), (2.11), and (2.44) give  , and the system (2.7) can be written as
, and the system (2.7) can be written as


Solving (2.46), we get

Then (2.45) turns into

Equation (2.48) can be solved in a similar way as in the proof of Theorem 2.1 using (1.18) (we omit details). We get

Formulas (2.47), (2.49) can be used in the case  as well. In this way, the ensuing result is proved.
as well. In this way, the ensuing result is proved.
Theorem 2.4.
Let (1.1) be a system with weak delay, (2.2) admit two repeated roots  , and the matrix
, and the matrix  has the form (2.6). Then
has the form (2.6). Then  and the solution of the initial problems (1.1) and (1.2) is
and the solution of the initial problems (1.1) and (1.2) is  ,
,  where
where  ,
,  is defined by (2.49) and
is defined by (2.49) and  by (2.47).
by (2.47).
2.2. Dimension of the Set of Solutions
Since all the possible cases of the planar system (1.1) with weak delay have been analysed, we are ready to formulate results concerning the dimension of the space of solutions of (1.1) assuming that initial conditions (1.2) are variable.
Theorem 2.5.
Let (1.1) be a system with weak delay, and (2.2) has both roots different from zero. Then the space of solutions, being initially  -dimensional, becomes on
-dimensional, becomes on  only
only
-
(1)
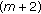 -dimensional if (2.2) has
-dimensional if (2.2) has-
(a)
two real distinct roots and

-
(b)
a two-fold real root,
 and
and 
-
(c)
a two-fold real root and
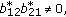
-
(a)
-
(2)
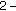 dimensional if (2.2) has
dimensional if (2.2) has-
(a)
two real distinct roots and

-
(b)
a pair of complex conjugate roots;
-
(c)
a two-fold real root and
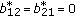 .
.
-
(a)
Proof.
We will carefully trace all theorems considered (Theorems 2.1–2.4) together with the case of a pair of complex conjugate roots uncovered by a theorem and our conclusion will hold on  (some of the statements hold on a greater interval).
(some of the statements hold on a greater interval).
-
(a)
Analysing the statement of Theorem 2.1 (the case (2.3) of two real distinct roots) we obtain the following subcases.
-
(a1)
If
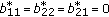 ,
, 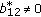 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on  equals
equals 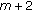 since the last line in (2.13) uses only
since the last line in (2.13) uses only  arbitrary parameters
arbitrary parameters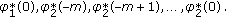 (250)
(250) -
(a2)
If
 ,
, 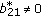 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 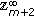 equals
equals 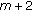 since the last line in (2.14) uses only
since the last line in (2.14) uses only  arbitrary parameters
arbitrary parameters (251)
(251) -
(a3)
If
 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 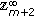 equals
equals 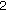 since the last line in (2.13) and in (2.14) uses only
since the last line in (2.13) and in (2.14) uses only  arbitrary parameters
arbitrary parameters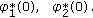 (252)
(252)
-
(a1)
This means that all the cases considered are covered by conclusions (1a) and (2a) of Theorem 2.5.
-
(b)
In the case (2.4) of two complex conjugate roots, we have
 and the formula (2.29) uses only
and the formula (2.29) uses only  arbitrary parameters
arbitrary parameters 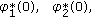 (253)
(253)
for every  . This is covered by case
. This is covered by case  of Theorem 2.5.
of Theorem 2.5.
-
(c)
Analysing the statement of Theorems 2.2 and 2.3 (the case (2.5) of two-fold real root), we obtain the following subcases.
-
(c1)
If
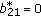 ,
, 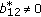 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on  equals
equals 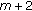 since the last line in (2.31) uses only
since the last line in (2.31) uses only 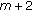 arbitrary parameters
arbitrary parameters (254)
(254) -
(c2)
If
 ,
,  , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 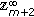 equals
equals 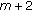 since the last line in (2.32) uses only
since the last line in (2.32) uses only  arbitrary parameters
arbitrary parameters (255)
(255) -
(c3)
If
 then the dimension of the space of solutions on
then the dimension of the space of solutions on 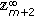 equals
equals 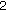 since the last line in (2.31) and in (2.32) uses only
since the last line in (2.31) and in (2.32) uses only  arbitrary parameters
arbitrary parameters (256)
(256) -
(c4)
If
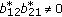 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on  equals
equals 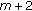 since the last line in (2.36) uses only
since the last line in (2.36) uses only  arbitrary parameters
arbitrary parameters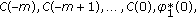 (257)
(257)
-
(c1)
where

The parameter  cannot be seen as independent since it depends on the independent parameters
cannot be seen as independent since it depends on the independent parameters  and
and  .
.
All the cases considered are covered by conclusions (1b), (1c), and (2c) of Theorem 2.5.
-
(d)
Analysing the statement of Theorem 2.4 (The case (2.6) of two-fold real root), we obtain the following subcases.
-
(d1)
If
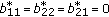 ,
, 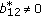 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 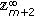 equals
equals 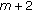 since the last line in (2.49) uses only
since the last line in (2.49) uses only 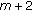 arbitrary parameters
arbitrary parameters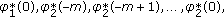 (259)
(259)and the last line in (2.47) provides no new information.
-
(d2)
If
 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 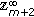 equals
equals  since, as follows from (2.49) and (2.47), there are only
since, as follows from (2.49) and (2.47), there are only  arbitrary parameters
arbitrary parameters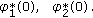 (260)
(260)
-
(d1)
Both cases are covered by conclusions (1b) and (2c) of Theorem 2.5.
Since there are no cases other than the above cases (a)–(d), the proof is finished.
Theorem 2.5 can be formulated simply as follows.
Theorem 2.6 (Main result).
Let (1.1) be a system with weak delay and let (2.2) have both roots different from zero. Then the space of solutions, being initially  -dimensional, is on
-dimensional, is on  only
only
-
(1)
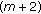 -dimensional if
-dimensional if  .
. -
(2)
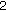 -dimensional if
-dimensional if 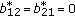 .
.
We omit the proofs of the following two theorems since again, they can be done in much the same way as Theorems 2.1–2.4.
Theorem 2.7.
Let (1.1) be a system with weak delay and let (2.2) have a simple root  . Then the space of solutions, being initially
. Then the space of solutions, being initially  -dimensional, is either
-dimensional, is either  -dimensional or
-dimensional or  -dimensional on
-dimensional on  .
.
Theorem 2.8.
Let (1.1) be a system with weak delay and let (2.2) have a two-fold root  . Then the space of solutions, being initially
. Then the space of solutions, being initially  -dimensional, turns into
-dimensional, turns into  -dimensional space on
-dimensional space on  , namely, into the zero solution.
, namely, into the zero solution.
3. Concluding Remarks
To our best knowledge, weak delay was first defined in [4] for systems of linear delayed differential systems with constant coefficients. Nevertheless, separate particular examples can be found in various books concerning delayed differential equations. Let us summarize the advantage of investigating "weak" delayed systems in the plane. Such systems can be simplified and their solutions can be found in a simple explicit analytical form. In the case of ordinary differential systems with delay, to obtain the corresponding eigenvalues, it is sufficient to solve only a polynomial equation rather than a quasipolynomial one. In the case of discrete systems of two equations investigated in this paper in the "weak" case, to obtain the corresponding eigenvalues, it is sufficient to solve only polynomial equation of the second order rather than a polynomial equation of  th order. Note that results obtained can be directly used to investigate such asymptotic problems as boundedness or convergence of solutions (using different methods, such problems have recently been investigated, e.g., in [5–11]).
th order. Note that results obtained can be directly used to investigate such asymptotic problems as boundedness or convergence of solutions (using different methods, such problems have recently been investigated, e.g., in [5–11]).
References
Baštinec J, Diblík J:Subdominant positive solutions of the discrete equation
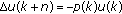 . Abstract and Applied Analysis 2004,2004(6):461-470. 10.1155/S1085337504306056
. Abstract and Applied Analysis 2004,2004(6):461-470. 10.1155/S1085337504306056Diblík J, Khusainov DYa: Representation of solutions of linear discrete systems with constant coefficients and pure delay. Advances in Difference Equations 2006, 2006:-13.
Elaydi SN: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. 3rd edition. Springer, New York, NY, USA; 2005:xxii+539.
Khusainov DYa, Benditkis DB, Diblík J: Weak delay in systems with an aftereffect. Functional Differential Equations 2002,9(3-4):385-404.
Boichuk A, Růžičková M: Solutions of nonlinear difference equations bounded on the whole line. Folia Facultatis Scientiarium Naturalium Universitatis Masarykiana Brunensis. Mathematica 2002, 13: 45-60.
Čermák J: On matrix differential equations with several unbounded delays. European Journal of Applied Mathematics 2006,17(4):417-433. 10.1017/S0956792506006590
Čermák J, Urbánek M: On the asymptotics of solutions of delay dynamic equations on time scales. Mathematical and Computer Modelling 2007,46(3-4):445-458. 10.1016/j.mcm.2006.11.015
Diblík J: Anti-Lyapunov method for systems of discrete equations. Nonlinear Analysis: Theory, Methods & Applications 2004,57(7-8):1043-1057. 10.1016/j.na.2004.03.030
Kipnis M, Komissarova D: Stability of a delay difference system. Advances in Difference Equations 2006, 2006:-9.
Liz E, Pituk M: Asymptotic estimates and exponential stability for higher-order monotone difference equations. Advances in Difference Equations 2005,2005(1):41-55. 10.1155/ADE.2005.41
Philos ChG, Purnaras IK: An asymptotic result for some delay difference equations with continuous variable. Advances in Difference Equations 2004,2004(1):1-10. 10.1155/S1687183904310058
Acknowledgments
The first author was supported by the Grant 201/07/0145 of Czech Grant Agency (Prague), by the Council of Czech Government MSM 00216 30503 and MSM 00216 30519. The third author was supported by the Council of Czech Government MSM 00216 30503 and MSM 00216 30529.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Diblík, J., Khusainov, D.Y. & Šmarda, Z. Construction of the General Solution of Planar Linear Discrete Systems with Constant Coefficients and Weak Delay. Adv Differ Equ 2009, 784935 (2009). https://doi.org/10.1155/2009/784935
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/784935
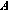 and Corresponding Solutions of The Problem (1.1), (1.2)
and Corresponding Solutions of The Problem (1.1), (1.2)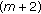 -dimensional if (2.2) has
-dimensional if (2.2) has
 and
and 
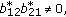
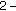 dimensional if (2.2) has
dimensional if (2.2) has
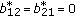 .
.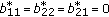 ,
, 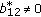 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on  equals
equals 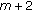 since the last line in (2.13) uses only
since the last line in (2.13) uses only  arbitrary parameters
arbitrary parameters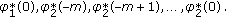
 ,
, 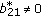 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 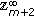 equals
equals 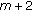 since the last line in (2.14) uses only
since the last line in (2.14) uses only  arbitrary parameters
arbitrary parameters
 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 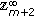 equals
equals 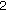 since the last line in (2.13) and in (2.14) uses only
since the last line in (2.13) and in (2.14) uses only  arbitrary parameters
arbitrary parameters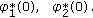
 and the formula (2.29) uses only
and the formula (2.29) uses only  arbitrary parameters
arbitrary parameters 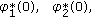
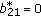 ,
, 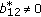 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on  equals
equals 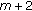 since the last line in (2.31) uses only
since the last line in (2.31) uses only 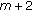 arbitrary parameters
arbitrary parameters
 ,
,  , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 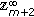 equals
equals 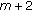 since the last line in (2.32) uses only
since the last line in (2.32) uses only  arbitrary parameters
arbitrary parameters
 then the dimension of the space of solutions on
then the dimension of the space of solutions on 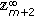 equals
equals 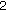 since the last line in (2.31) and in (2.32) uses only
since the last line in (2.31) and in (2.32) uses only  arbitrary parameters
arbitrary parameters
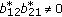 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on  equals
equals 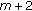 since the last line in (2.36) uses only
since the last line in (2.36) uses only  arbitrary parameters
arbitrary parameters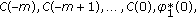
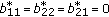 ,
, 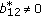 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 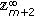 equals
equals 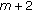 since the last line in (2.49) uses only
since the last line in (2.49) uses only 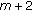 arbitrary parameters
arbitrary parameters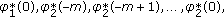
 , then the dimension of the space of solutions on
, then the dimension of the space of solutions on 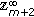 equals
equals  since, as follows from (2.49) and (2.47), there are only
since, as follows from (2.49) and (2.47), there are only  arbitrary parameters
arbitrary parameters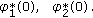
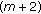 -dimensional if
-dimensional if  .
.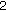 -dimensional if
-dimensional if 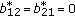 .
.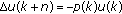 . Abstract and Applied Analysis 2004,2004(6):461-470. 10.1155/S1085337504306056
. Abstract and Applied Analysis 2004,2004(6):461-470. 10.1155/S1085337504306056