- Research Article
- Open access
- Published:
Impulsive Periodic Boundary Value Problems for Dynamic Equations on Time Scale
Advances in Difference Equations volume 2009, Article number: 603271 (2009)
Abstract
Let T be a periodic time scale with period  such that
such that  , and
, and  . Assume each
. Assume each  is dense. Using Schaeffer's theorem, we show that the impulsive dynamic equation
is dense. Using Schaeffer's theorem, we show that the impulsive dynamic equation  where
where  ,
,  , and
, and  is the
is the  -derivative on T, has a solution.
-derivative on T, has a solution.
1. Introduction
Due to their importance in numerous application, for example, physics, population dynamics, industrial robotics, optimal control, and other areas, many authors are studying dynamic equations with impulse effects; see [1 - 19] and references therein.
The primary motivation for this work are the papers by Kaufmann et al. [9] and Li et al. [12]. In [9], the authors used a fixed point theorem due to Krasnosel'skiĭ to establish the existence theorems for the impulsive dynamic equation:

where  and
and  is the
is the  -derivative on
-derivative on  .
.
In [12], the authors gave sufficient conditions for the existence of solutions for the impulsive periodic boundary value problem equation:

where  , and
, and  . This paper extends and generalized the above results to dynamic equations on time scales.
. This paper extends and generalized the above results to dynamic equations on time scales.
We assume the reader is familiar with the notation and basic results for dynamic equations on time scales. While the books [20, 21] are indispensable resources for those who study dynamic equations on time scales, these manuscripts do not explicitly cover the concept of periodicity. The following definitions are essential in our analysis.
Definition 1.1 (see [8]).
We say that a time scale  is periodic if there exist a
is periodic if there exist a  such that if
such that if  , then
, then  . For
. For  , the smallest positive
, the smallest positive  is called the period of the time scale.
is called the period of the time scale.
Example 1.2.
The following time scales are periodic:
-
(1)
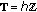 has period
has period 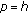 ,
, -
(2)
 ,
, -
(3)
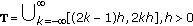 has period
has period  ,
, -
(4)
 , where
, where  , has period
, has period 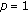 .
.
Remark 1.3.
All periodic time scales are unbounded above and below.
Definition 1.4.
Let  be a periodic time scale with period
be a periodic time scale with period  . We say that the function
. We say that the function  is periodic with period
is periodic with period  if there exists a natural number
if there exists a natural number  such that
such that  ,
,  for all
for all  and
and  is the smallest number such that
is the smallest number such that  .
.
If  , we say that
, we say that  is periodic with period
is periodic with period  if
if  is the smallest positive number such that
is the smallest positive number such that  for all
for all  .
.
Remark 1.5.
If  is a periodic time scale with period
is a periodic time scale with period  , then
, then  . Consequently, the graininess function
. Consequently, the graininess function  satisfies
satisfies  and so, is a periodic function with period
and so, is a periodic function with period  .
.
Let  be a periodic time scale with period
be a periodic time scale with period  such that
such that  , for
, for  , where
, where  for some
for some  ,
,  , and assume that each
, and assume that each  is dense in
is dense in  for each
for each  . We show the existence of solutions for the nonlinear periodic impulsive dynamic equation:
. We show the existence of solutions for the nonlinear periodic impulsive dynamic equation:

where  and
and  . Define
. Define  and note that the intervals
and note that the intervals  and
and  are defined similarly.
are defined similarly.
In Section 2 we present some preliminary ideas that will be used in the remainder of the paper. In Section 3 we give sufficient conditions for the existence of at least one solution of the nonlinear problem (1.3).
2. Preliminaries
In this section we present some important concepts found in [20, 21] that will be used throughout the paper. We also define the space in which we seek solutions, state Schaeffer's theorem, and invert the linearized dynamic equation.
A function  is said to be regressive provided
is said to be regressive provided  for all
for all  . The set of all regressive rd-continuous functions
. The set of all regressive rd-continuous functions  is denoted by
is denoted by  .
.
Let  and
and  for all
for all  . The exponential function on
. The exponential function on  , defined by
, defined by

is the solution to the initial value problem  . Other properties of the exponential function are given in the following lemma, [20, Theorem 2.36].
. Other properties of the exponential function are given in the following lemma, [20, Theorem 2.36].
Lemma 2.1.
Let  . Then
. Then
-
(i)
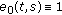 and
and 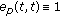 ;
; -
(ii)
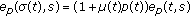 ;
; -
(iii)
 where,
where, 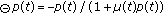 ;
; -
(iv)
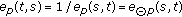 ;
; -
(v)
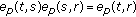 ;
; -
(vi)
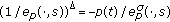 .
.
Define  and let
and let  . For
. For  , let
, let  . Define
. Define

and

where  is the space of all real-valued continuous functions on
is the space of all real-valued continuous functions on  , and
, and  is the space of all continuously delta-differentiable functions on
is the space of all continuously delta-differentiable functions on  . The set
. The set  is a Banach space when it is endowed with the supremum norm:
is a Banach space when it is endowed with the supremum norm:

where  .
.
We employ Schaeffer's fixed point theorem, see [22], to prove the existence of a periodic solution.
Theorem 2.2 (Schaeffer's Theorem).
Let  be a normed linear space and let the operator
be a normed linear space and let the operator  be compact. Define
be compact. Define

Then either
-
(i)
the set
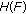 is unbounded, or
is unbounded, or -
(ii)
the operator
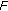 has a fixed point in
has a fixed point in 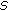 .
.
The following conditions hold throughout the paper:
-
(A)
 is periodic with period
is periodic with period  ;
; 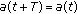 for all
for all 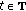 .
. -
(F)
 and for all
and for all 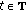 ,
, 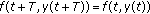 .
.
Furthermore, to ensure that the boundary value problem is not at resonance, we assume that  .
.
Consider the linear boundary value problem:

where  . Our first result inverts the operator (2.6).
. Our first result inverts the operator (2.6).
Lemma 2.3.
The function  is a solution of (2.6) if and only if
is a solution of (2.6) if and only if  is a solution of
is a solution of

where

Proof.
It is easy to see that if  is a solution of (2.6), then for
is a solution of (2.6), then for  we have
we have

Apply the periodic boundary condition  to obtain
to obtain

Since  , we can solve the above equation for
, we can solve the above equation for  . Thus,
. Thus,

Substitute (2.11) into (2.9). Since  , we have, for all
, we have, for all  ,
,

We can rewrite this equation as follows:

Since  , then
, then

That is,  satisfies (2.7).
satisfies (2.7).
The converse follows trivially and the proof is complete.
3. The Nonlinear Problem
In this section we give sufficient conditions for the existence of periodic solutions of (1.3). To this end, define the operator  by
by

Then  is a solution of (1.3) if and only if
is a solution of (1.3) if and only if  is a fixed point of
is a fixed point of  . A standard application of the Arzelà-Ascoli theorem yields that
. A standard application of the Arzelà-Ascoli theorem yields that  is compact.
is compact.
Our first result is an existence and uniqueness theorem.
Theorem 3.1.
Suppose there exist constants  and
and  for which
for which

and

and such that

Then there exists a unique solution to (1.3).
Proof.
We will show that there exists a unique solution  of (3.1). By Lemma 2.3 this solution is the unique solution of (1.3).
of (3.1). By Lemma 2.3 this solution is the unique solution of (1.3).
Let  . Then for all
. Then for all 

Hence,  . By the Contraction Mapping Principal, there exists a unique solution of (3.1) and the proof is complete.
. By the Contraction Mapping Principal, there exists a unique solution of (3.1) and the proof is complete.
Our next two results utilize Theorem 2.2 to establish the existence of solutions of (1.3).
Theorem 3.2.
Assume there exist functions  with
with

such that

Suppose that  . Then there exists at least one solution of (1.3).
. Then there exists at least one solution of (1.3).
Proof.
Define

and let  . We show
. We show  is bounded by a constant that depends only on the constants
is bounded by a constant that depends only on the constants  , and
, and  . For all
. For all  ,
,


 Consequently,
Consequently,

which implies that  We have that if
We have that if  , then
, then  is bounded by the constant
is bounded by the constant  The set
The set  is bounded and so by Schaeffer's theorem, the operator
is bounded and so by Schaeffer's theorem, the operator  has a fixed point. This fixed point is a solution of (1.3) and the proof is complete.
has a fixed point. This fixed point is a solution of (1.3) and the proof is complete.
In our next theorem we assume that  and
and  are sublinear at infinity with respect to the second variable.
are sublinear at infinity with respect to the second variable.
Theorem 3.3.
Assume that
(FI) , uniformly, and
, uniformly, and
(I) , uniformly.
, uniformly.
Then there exists at least one solution of the boundary value problem (1.3).
Proof.
Suppose that the set

is unbounded. Then there exists sequences  and
and  , with
, with  and
and  , such that
, such that

Define  . Then
. Then  and
and

By conditions ( ) and (
) and ( ) we have
) we have


From (3.13), (3.14), and (3.15), we have that

as  , which contradicts
, which contradicts  for all
for all  . Thus the set
. Thus the set  is bounded. By Theorem 2.2, the operator
is bounded. By Theorem 2.2, the operator  has a fixed point. This fixed point is a solution of (1.3) and the proof is complete.
has a fixed point. This fixed point is a solution of (1.3) and the proof is complete.
The following corollary is an immediate consequences of Theorem 3.3
Corollary 3.4.
Assume that  and
and  are bounded. Then there exists at least one solution of (1.3).
are bounded. Then there exists at least one solution of (1.3).
References
Baĭnov DD, Simeonov PS: Systems with Impulse Effect: Stability, Theory and Application, Ellis Horwood Series: Mathematics and Its Applications. Ellis Horwood, Chichester, UK; 1989:255.
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: On first order impulsive dynamic equations on time scales. Journal of Difference Equations and Applications 2004,10(6):541-548. 10.1080/10236190410001667986
Geng F, Xu Y, Zhu D: Periodic boundary value problems for first-order impulsive dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):4074-4087. 10.1016/j.na.2007.10.038
Graef JR, Ouahab A: Extremal solutions for nonresonance impulsive functional dynamic equations on time scales. Applied Mathematics and Computation 2008,196(1):333-339. 10.1016/j.amc.2007.05.056
Guo D: Existence of positive solutions for nth-order nonlinear impulsive singular integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,68(9):2727-2740. 10.1016/j.na.2007.02.019
Guo D: A class of second-order impulsive integro-differential equations on unbounded domain in a Banach space. Applied Mathematics and Computation 2002,125(1):59-77. 10.1016/S0096-3003(00)00115-6
Guo D: Multiple positive solutions of a boundary value problem for nth-order impulsive integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2005,63(4):618-641. 10.1016/j.na.2005.05.023
Kaufmann ER, Raffoul YN: Periodic solutions for a neutral nonlinear dynamical equation on a time scale. Journal of Mathematical Analysis and Applications 2006,319(1):315-325. 10.1016/j.jmaa.2006.01.063
Kaufmann ER, Kosmatov N, Raffoul YN: Impulsive dynamic equations on a time scale. Electronic Journal of Differential Equations 2008,2008(67):1-9.
Kaufmann ER, Kosmatov N, Raffoul YN: A second-order boundary value problem with impulsive effects on an unbounded domain. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):2924-2929. 10.1016/j.na.2007.08.061
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1994.
Li J, Nieto JJ, Shen J: Impulsive periodic boundary value problems of first-order differential equations. Journal of Mathematical Analysis and Applications 2007,325(1):226-236. 10.1016/j.jmaa.2005.04.005
Liu X: Nonlinear boundary value problems for first order impulsive integro-differential equations. Applicable Analysis 1990,36(1-2):119-130. 10.1080/00036819008839925
Nieto JJ: Basic theory for nonresonance impulsive periodic problems of first order. Journal of Mathematical Analysis and Applications 1997,205(2):423-433. 10.1006/jmaa.1997.5207
Pierson-Gorez C: Impulsive differential equations of first order with periodic boundary conditions. Differential Equations and Dynamical Systems 1993,1(3):185-196.
Rogovchenko YV: Impulsive evolution systems: main results and new trends. Dynamics of Continuous, Discrete and Impulsive Systems 1997,3(1):57-88.
Samoĭlenko AM, Perestyuk NA: Impulsive Differential Equations, World Scientific Series on Nonlinear Science, Series A: Monographs and Treatises. Volume 14. World Scientific, River Edge, NJ, USA; 1995:x+462.
Vatsala AS, Sun Y: Periodic boundary value problems of impulsive differential equations. Applicable Analysis 1992,44(3-4):145-158. 10.1080/00036819208840074
Wang D-B: Positive solutions for nonlinear first-order periodic boundary value problems of impulsive dynamic equations on time scales. Computers & Mathematics with Applications 2008,56(6):1496-1504. 10.1016/j.camwa.2008.02.038
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Smart DR: Fixed Point Theorems. Cambridge University Press, London, UK; 1980.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kaufmann, E.R. Impulsive Periodic Boundary Value Problems for Dynamic Equations on Time Scale. Adv Differ Equ 2009, 603271 (2009). https://doi.org/10.1155/2009/603271
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/603271
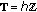 has period
has period 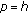 ,
, ,
,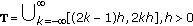 has period
has period  ,
, , where
, where  , has period
, has period 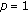 .
.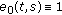 and
and 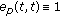 ;
;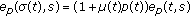 ;
; where,
where, 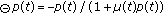 ;
;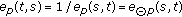 ;
;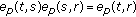 ;
;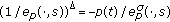 .
.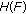 is unbounded, or
is unbounded, or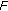 has a fixed point in
has a fixed point in 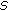 .
. is periodic with period
is periodic with period  ;
; 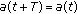 for all
for all 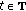 .
. and for all
and for all 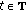 ,
, 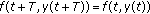 .
.