- Research Article
- Open access
- Published:
Stability of an Additive-Cubic-Quartic Functional Equation
Advances in Difference Equations volume 2009, Article number: 395693 (2010)
Abstract
In this paper, we consider the additive-cubic-quartic functional equation  and prove the generalized Hyers-Ulam stability of the additive-cubic-quartic functional equation in Banach spaces.
and prove the generalized Hyers-Ulam stability of the additive-cubic-quartic functional equation in Banach spaces.
1. Introduction
The stability problem of functional equations is originated from a question of Ulam [1] concerning the stability of group homomorphisms. Hyers [2] gave a first affirmative partial answer to the question of Ulam for Banach spaces. Hyers' Theorem was generalized by Aoki [3] for additive mappings and by Rassias [4] for linear mappings by considering an unbounded Cauchy difference. The paper of Rassias [4] has provided a lot of influence in the development of what we callgeneralized Hyers-Ulam stability or asHyers-Ulam-Rassias stability of functional equations. A generalization of the Rassias theorem was obtained by G vruta [8] by replacing the unbounded Cauchy difference by a general control function in the spirit of Rassias' approach (see [2, 5–13]).
vruta [8] by replacing the unbounded Cauchy difference by a general control function in the spirit of Rassias' approach (see [2, 5–13]).
Jun and Kim [14] introduced and investigate the following functional equation:

and prove the generalized Hyers-Ulam stability for the functional equation (1.1). Obviously, the function  satisfies the functional equation (1.1), which is called a cubic functional equation. Every solution of the cubic functional equation is said to be a cubic mapping. Jun and Kim proved that a mapping
satisfies the functional equation (1.1), which is called a cubic functional equation. Every solution of the cubic functional equation is said to be a cubic mapping. Jun and Kim proved that a mapping  between two real vector spaces
between two real vector spaces  and
and  is a solution of (1.1) if and only if there exists a unique mapping
is a solution of (1.1) if and only if there exists a unique mapping  such that
such that  for all
for all  ; moreover,
; moreover,  is symmetric for each fixed one variable and is additive for fixed two variables.
is symmetric for each fixed one variable and is additive for fixed two variables.
In [15], Park and Bae considered the following quartic functional equation:

In fact, they proved that a mapping  between two real vector spaces
between two real vector spaces  and
and  is a solution of (1.2) if and only if there exists a unique symmetric multi-additive mapping
is a solution of (1.2) if and only if there exists a unique symmetric multi-additive mapping  such that
such that  for all
for all  (see [7, 11]). It is easy to show that the function
(see [7, 11]). It is easy to show that the function  satisfies the functional equation (1.2), which is called a quartic functional equation. Every solution of the quartic functional equation is said to be a quartic mapping.
satisfies the functional equation (1.2), which is called a quartic functional equation. Every solution of the quartic functional equation is said to be a quartic mapping.
In this paper, we aim to deal with the next functional equation derived from additive, cubic, and quadric mappings,

It is easy to show that the function  satisfies the functional equation (1.3). We establish the general solution and prove the generalized Hyers-Ulam stability for the functional equation (1.3).
satisfies the functional equation (1.3). We establish the general solution and prove the generalized Hyers-Ulam stability for the functional equation (1.3).
2. An Additive-Cubic-Quartic Functional Equation
Throughout this section,  and
and  will be real vector spaces. Before proceeding the proof of Theorem 2.4 which is the main result in this section, we shall need the following two lemmas.
will be real vector spaces. Before proceeding the proof of Theorem 2.4 which is the main result in this section, we shall need the following two lemmas.
Lemma 2.1.
If an even mapping  satisfies (1.3), then
satisfies (1.3), then  is quartic.
is quartic.
Proof.
Putting  in (1.3), we get
in (1.3), we get  . Setting
. Setting  in (1.3), by the evenness of
in (1.3), by the evenness of  , we obtain
, we obtain

for all  . Hence (1.3) can be written as
. Hence (1.3) can be written as

for all  . Replacing
. Replacing  by
by  in (1.3), we obtain
in (1.3), we obtain

for all  . By (2.1) and (2.3), we obtain
. By (2.1) and (2.3), we obtain

for all  . According to (2.4), (2.2) can be written as
. According to (2.4), (2.2) can be written as

for all  . This shows that
. This shows that  is quartic, which completes the proof of the lemma.
is quartic, which completes the proof of the lemma.
Lemma 2.2.
If an odd mapping  satisfies (1.3), then f is cubic-additive.
satisfies (1.3), then f is cubic-additive.
Proof.
We show that the mappings  and
and  , respectively, defined by
, respectively, defined by  and
and  , are additive and cubic, respectively.
, are additive and cubic, respectively.
Since  is odd,
is odd,  . Letting
. Letting  in (1.3), we obtain
in (1.3), we obtain

for all  . Hence (1.3) can be written as
. Hence (1.3) can be written as

for all  . Replacing
. Replacing  by
by  and
and  in (2.7), respectively, we get
in (2.7), respectively, we get

for all  . Replacing
. Replacing  by
by  in (2.7), we obtain
in (2.7), we obtain

for all  . Replacing
. Replacing  by
by  in (2.9), we get
in (2.9), we get

for all  . Replacing
. Replacing  by
by  and
and  by
by  in (2.9), we get
in (2.9), we get

for all  . Replacing
. Replacing  by
by  in (2.11), we get
in (2.11), we get

for all  .
.
Subtracting (2.12) from (2.10), we obtain

for all  . By (2.8) and (2.13), we obtain
. By (2.8) and (2.13), we obtain

for all  .
.
Replacing  by
by  in (2.14), we get
in (2.14), we get

for all  .
.
By (2.14) and (2.15), we obtain

for all  .
.
By (2.7) and (2.16), we have

for all  . Replacing
. Replacing  by
by  in (2.17), we get
in (2.17), we get

for all  . Replacing
. Replacing  by
by  in (2.18), respectively, we get
in (2.18), respectively, we get

for all  .
.
By (2.18) and (2.19), we obtain

for all  . Replacing
. Replacing  by
by  in (2.17), respectively, we get
in (2.17), respectively, we get

for all  . Thus it follows from (2.20) and (2.21) that
. Thus it follows from (2.20) and (2.21) that

for all  . Replacing
. Replacing  by
by  in (2.22), we obtain
in (2.22), we obtain

for all  . Replacing
. Replacing  by
by  in (2.23), respectively, we get
in (2.23), respectively, we get

for all  . By (2.23) and (2.24), we obtain
. By (2.23) and (2.24), we obtain

for all  . Adding (2.22) to (2.25) and using (2.17), we get
. Adding (2.22) to (2.25) and using (2.17), we get

for all  . The last equality means that
. The last equality means that

for all  Thus the mapping
Thus the mapping  is additive.
is additive.
Replacing  by
by  in (2.17), respectively, we get
in (2.17), respectively, we get

for all  . Since
. Since  for all
for all 

for all  Hence it follows from (2.17) and (2.28) that
Hence it follows from (2.17) and (2.28) that

for all  Thus the mapping
Thus the mapping  is cubic.
is cubic.
On the other hand, we have  for all
for all  This means that
This means that  is cubic-additive. This completes the proof of the lemma.
is cubic-additive. This completes the proof of the lemma.
The following is suggested by an anonymous referee.
Remark 2.3.
The functional equation (1.3) is equivalent to the functional equation

The left hand side is even with respect to  and the right hand side is odd by the assumption of Lemma 2.2. Thus
and the right hand side is odd by the assumption of Lemma 2.2. Thus

So we conclude that  , as desired.
, as desired.
Theorem 2.4.
If a mapping  satisfies (1.3) for all
satisfies (1.3) for all  , then there exist a unique additive mapping
, then there exist a unique additive mapping  a unique mapping
a unique mapping  , and a unique symmetric multi-additive mapping
, and a unique symmetric multi-additive mapping  such that
such that  for all
for all  and that
and that  is symmetric for each fixed one variable and is additive for fixed two variables.
is symmetric for each fixed one variable and is additive for fixed two variables.
Proof.
Let  satisfy (1.3). We decompose
satisfy (1.3). We decompose  into the even part and the odd part by setting
into the even part and the odd part by setting

for all  By (1.3), we have
By (1.3), we have

for all  This means that
This means that  satisfies (1.3). Similarly we can show that
satisfies (1.3). Similarly we can show that  satisfies (1.3). By Lemmas 2.1 and 2.2,
satisfies (1.3). By Lemmas 2.1 and 2.2,  and
and  are quartic and cubic-additive, respectively. Thus there exist a unique additive mapping
are quartic and cubic-additive, respectively. Thus there exist a unique additive mapping  a unique mapping
a unique mapping  , and a unique symmetric multi-additive mapping
, and a unique symmetric multi-additive mapping  such that
such that  and that
and that  for all
for all  and
and  is symmetric for each fixed one variable and is additive for fixed two variables. Thus
is symmetric for each fixed one variable and is additive for fixed two variables. Thus  for all
for all  as desired.
as desired.
3. Stability of an Additive-Cubic-Quartic Functional Equation
We now investigate the generalized Hyers-Ulam stability problem of the functional equation (1.3). From now on, let  be a real vector space and let
be a real vector space and let  be a Banach space. Now before taking up the main subject, given
be a Banach space. Now before taking up the main subject, given  , we define the difference operator
, we define the difference operator  by
by

for all  We consider the following functional inequality:
We consider the following functional inequality:

for an upper bound 
Theorem 3.1.
Let  be fixed. Suppose that an even mapping
be fixed. Suppose that an even mapping  satisfies
satisfies  and
and

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then the limit
then the limit

exists for all  and
and  is a unique quartic mapping satisfying (1.3) and
is a unique quartic mapping satisfying (1.3) and

for all 
Proof.
Putting  in (3.3), we obtain
in (3.3), we obtain

for all  On the other hand, replacing
On the other hand, replacing  by
by  in (3.3), we get
in (3.3), we get

for all  By (3.7) and (3.8), we get
By (3.7) and (3.8), we get

for all  Replacing
Replacing  by
by  in (3.9), we get
in (3.9), we get

for all  . It follows from (3.10) that
. It follows from (3.10) that

for all  . It follows from (3.11) that
. It follows from (3.11) that

for all  .
.
This shows that  is a Cauchy sequence in
is a Cauchy sequence in  . Since
. Since  is complete, the sequence
is complete, the sequence  converges. We now define
converges. We now define  by
by

for all  It is clear that (3.6) holds, and
It is clear that (3.6) holds, and  for all
for all  By (3.3), we have
By (3.3), we have

for all  Hence by Lemma 2.1,
Hence by Lemma 2.1,  is quartic.
is quartic.
It remains to show that  is unique. Suppose that there exists a quartic mapping
is unique. Suppose that there exists a quartic mapping  which satisfies (1.3) and (3.6). Since
which satisfies (1.3) and (3.6). Since  and
and  for all
for all  we conclude that
we conclude that

for all  . By taking
. By taking  in this inequality, we have
in this inequality, we have  for all
for all  which gives the conclusion for the case
which gives the conclusion for the case  Let
Let  Then by (3.9), we have
Then by (3.9), we have

for all  Replacing
Replacing  by
by  in (3.16) and dividing by 16, we get
in (3.16) and dividing by 16, we get

for all  By (3.16) and (3.17), we obtain
By (3.16) and (3.17), we obtain

for all  It follows from (3.18) that
It follows from (3.18) that

for all  Dividing both sides of (3.19) by
Dividing both sides of (3.19) by  and then replacing
and then replacing  by
by  , we get
, we get

for all  By taking
By taking  in (3.20),
in (3.20),  is a Cauchy sequence in
is a Cauchy sequence in  . Then
. Then  exists for all
exists for all  It is easy to see that (3.6) holds for
It is easy to see that (3.6) holds for 
The rest of the proof is similar to the case 
Theorem 3.2.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then the limit
then the limit

exists for all  and
and  is a unique additive mapping satisfying (1.3) and
is a unique additive mapping satisfying (1.3) and

for all 
Proof.
Set  in (3.21). Then by the oddness of
in (3.21). Then by the oddness of  , we have
, we have

for all  Replacing
Replacing  by
by  in (3.21), we obtain
in (3.21), we obtain

for all  . Combining (3.25) and (3.26) yields that
. Combining (3.25) and (3.26) yields that

for all  Putting
Putting  and
and  for all
for all  we get
we get

for all  . It follows from (3.28) that
. It follows from (3.28) that

for all  Multiplying both sides of (3.29) by
Multiplying both sides of (3.29) by  and then replacing
and then replacing  by
by  , we get
, we get

for all  So
So  is a Cauchy sequence in
is a Cauchy sequence in  . Put
. Put  for all
for all  Then we have
Then we have

for all  . On the other hand, it is easy to show that
. On the other hand, it is easy to show that

for all  Hence it follows that
Hence it follows that

for all  This means that
This means that  satisfies (1.3). Then by Lemma 2.2,
satisfies (1.3). Then by Lemma 2.2,  is additive. Thus (3.31) implies that
is additive. Thus (3.31) implies that  is additive.
is additive.
To prove the uniqueness of  , suppose that
, suppose that  is an additive mapping satisfying (3.24). Then for every
is an additive mapping satisfying (3.24). Then for every  we have
we have  and
and  Hence it follows that
Hence it follows that

for all  . This shows that
. This shows that  for all
for all 
Theorem 3.3.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that

for all  then the limit
then the limit

exists for all  and
and  is a unique cubic mapping satisfying (1.3), and
is a unique cubic mapping satisfying (1.3), and

for all 
Proof.
It is easy to show that  satisfies (3.27). Setting
satisfies (3.27). Setting  and then putting
and then putting  in (3.27), we obtain
in (3.27), we obtain

for all  It follows from (3.40) that
It follows from (3.40) that

for all  . Replacing
. Replacing  by
by  in (3.41) and then multiplying both sides of (3.41) by
in (3.41) and then multiplying both sides of (3.41) by  we get
we get

for all  . Since the right hand side of the inequality (3.42) tends to 0 as
. Since the right hand side of the inequality (3.42) tends to 0 as  the sequence
the sequence  is Cauchy. Now we define
is Cauchy. Now we define

for all  Then we have
Then we have

for all  Let
Let

for all  . Then we have
. Then we have

for all  . Since
. Since  is an odd mapping,
is an odd mapping,  satisfies (2.6). By (3.44), we conclude that
satisfies (2.6). By (3.44), we conclude that  for all
for all  Then
Then  is cubic.
is cubic.
We have to show that  is unique. Suppose that there exists another cubic mapping
is unique. Suppose that there exists another cubic mapping  which satisfies (1.3) and (3.39). Since
which satisfies (1.3) and (3.39). Since  and
and  for all
for all  we have
we have

for all  By letting
By letting  in the above inequality, we get
in the above inequality, we get  for all
for all  which gives the conclusion.
which gives the conclusion.
Theorem 3.4.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then there exist a unique cubic mapping
then there exist a unique cubic mapping  , and a unique additive mapping
, and a unique additive mapping  such that
such that

for all 
Proof.
By Theorems 3.2 and 3.3, there exist an additive mapping  and a cubic mapping
and a cubic mapping  such that
such that

for all  Combining two equations in (3.51) yields that
Combining two equations in (3.51) yields that

for all  So we get (3.50) by letting
So we get (3.50) by letting  and
and  for all
for all 
To prove the uniqueness of  and
and  let
let  be other additive and cubic mappings satisfying (3.50). Let
be other additive and cubic mappings satisfying (3.50). Let  Then
Then

for all  Since
Since

for all  Hence (3.53) implies that
Hence (3.53) implies that

for all  Since
Since  , by (3.55), we obtain that
, by (3.55), we obtain that  for all
for all  Again by (3.55), we have
Again by (3.55), we have  for all
for all 
Now we prove the generalized Hyers-Ulam stability of the functional equation (1.3).
Theorem 3.5.
Suppose that a mapping  satisfies
satisfies  and
and  for all
for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then there exist a unique additive mapping
then there exist a unique additive mapping  a unique cubic mapping
a unique cubic mapping  , and a unique quartic mapping
, and a unique quartic mapping  such that
such that

for all  .
.
Proof.
Let  for all
for all  Then
Then 
 and
and

for all  Hence in view of Theorem 3.1, there exists a unique quartic mapping
Hence in view of Theorem 3.1, there exists a unique quartic mapping  satisfying (3.6). Let
satisfying (3.6). Let  for all
for all  Then
Then 
 , and
, and  for all
for all  From Theorem 3.4, it follows that there exist a unique cubic mapping
From Theorem 3.4, it follows that there exist a unique cubic mapping  and a unique additive mapping
and a unique additive mapping  satisfying (3.44). Now it is obvious that (3.57) holds for all
satisfying (3.44). Now it is obvious that (3.57) holds for all  and the proof of the theorem is complete.
and the proof of the theorem is complete.
Corollary 3.6.
Let  and let
and let  be a positive real number. Suppose that a mapping
be a positive real number. Suppose that a mapping  satisfies
satisfies  and
and

for all  Then there exist a unique additive mapping
Then there exist a unique additive mapping  a unique cubic mapping
a unique cubic mapping  , and a unique quartic mapping
, and a unique quartic mapping  satisfying
satisfying

for all  .
.
Proof.
It follows from Theorem 3.5 by taking  for all
for all  .
.
Theorem 3.7.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then the limit
then the limit

exists for all  and
and  is a unique additive mapping satisfying (1.3) and
is a unique additive mapping satisfying (1.3) and

for all 
Proof.
The proof is similar to the proof of Theorem 3.2.
Employing a similar way to the proof of Theorem 3.3, we get the following theorem.
Theorem 3.8.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then the limit
then the limit

exists for all  and
and  is a unique cubic mapping satisfying (1.3), and
is a unique cubic mapping satisfying (1.3), and

for all 
Theorem 3.9.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then there exist a unique additive mapping
then there exist a unique additive mapping  , and a unique cubic mapping
, and a unique cubic mapping  such that
such that

for all 
Proof.
The proof is similar to the proof of Theorem 3.4.
Theorem 3.10.
Suppose that  satisfies
satisfies  and
and

for all  If the upper bound
If the upper bound  is a function such that
is a function such that

and that  for all
for all  then there exist a unique additive mapping
then there exist a unique additive mapping  a unique cubic mapping
a unique cubic mapping  , and a unique quartic mapping
, and a unique quartic mapping  such that
such that

for all  .
.
Proof.
The proof is similar to the proof of Theorem 3.5.
Corollary 3.11.
Let  and let
and let  be a positive real number. Suppose that
be a positive real number. Suppose that  satisfies
satisfies  and
and

for all  Then there exist a unique additive mapping
Then there exist a unique additive mapping  a unique cubic mapping
a unique cubic mapping  , and a unique quartic mapping
, and a unique quartic mapping  satisfying
satisfying

for all  .
.
Corollary 3.12.
Let  be a positive real number. Suppose that a mapping
be a positive real number. Suppose that a mapping  satisfies
satisfies  and
and  for all
for all  Then there exist a unique additive mapping
Then there exist a unique additive mapping  a unique cubic mapping
a unique cubic mapping  , and a unique quartic mapping
, and a unique quartic mapping  such that
such that

for all  .
.
References
Ulam SM: Problems in Modern Mathematics. Science edition. John Wiley & Sons, New York, NY, USA; 1940.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222-224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64-66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297-300. 10.1090/S0002-9939-1978-0507327-1
Gajda Z: On stability of additive mappings. International Journal of Mathematics and Mathematical Sciences 1991,14(3):431-434. 10.1155/S016117129100056X
Aczél J, Dhombres J: Functional Equations in Several Variables, Encyclopedia of Mathematics and Its Applications. Volume 31. Cambridge University Press, Cambridge, UK; 1989:xiv+462.
Cholewa PW: Remarks on the stability of functional equations. Aequationes Mathematicae 1984,27(1-2):76-86.
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431-436. 10.1006/jmaa.1994.1211
Grabiec A: The generalized Hyers-Ulam stability of a class of functional equations. Publicationes Mathematicae Debrecen 1996,48(3-4):217-235.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and their Applications, 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Isac G, Rassias ThM:On the Hyers-Ulam stability of
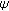 -additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010
-additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010Rassias ThM (Ed): Functional Equations and Inequalities, Mathematics and Its Applications. Volume 518. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xii+336.
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000,251(1):264-284. 10.1006/jmaa.2000.7046
Jun K-W, Kim H-M: The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. Journal of Mathematical Analysis and Applications 2002,274(2):267-278.
Park W-G, Bae J-H: On a bi-quadratic functional equation and its stability. Nonlinear Analysis. Theory, Methods & Applications 2005,62(4):643-654. 10.1016/j.na.2005.03.075
Acknowledgments
The authors would like to thank the referees for a number of valuable suggestions regarding a previous version of this paper. The third and corresponding author was supported by Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (NRF-2009-0070788).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Eshaghi-Gordji, M., Kaboli-Gharetapeh, S., Park, C. et al. Stability of an Additive-Cubic-Quartic Functional Equation. Adv Differ Equ 2009, 395693 (2010). https://doi.org/10.1155/2009/395693
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/395693
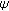 -additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010
-additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010