- Research Article
- Open access
- Published:
Stabilization of Discrete-Time Control Systems with Multiple State Delays
Advances in Difference Equations volume 2009, Article number: 240707 (2009)
Abstract
We give sufficient conditions for the exponential stabilizability of a class of perturbed time-varying difference equations with multiple delays and slowly varying coefficients. Under appropiate growth conditions on the perturbations, combined with the "freezing" technique, we establish explicit conditions for global feedback exponential stabilizability.
1. Introduction
Let us consider a discrete-time control system described by the following equationin :
:


where  denotes the
denotes the  dimensional space of complex column vectors,
dimensional space of complex column vectors,  is a given integer,
is a given integer,  is the state,
is the state,  (
( ) is the input,
) is the input,  is the set of nonnegative integers. Hence forward,
is the set of nonnegative integers. Hence forward,  is the Euclidean norm;
is the Euclidean norm;  and
and  are variable matrices of compatible dimensions,
are variable matrices of compatible dimensions,  is a variable
is a variable  matrix such that
matrix such that

and  is a given vector-valued function, that is,
is a given vector-valued function, that is, 
The stabilizability question consists on finding a feedback control law  for keeping the closed-loop system
for keeping the closed-loop system

asymptotically stable in the Lyapunov sense.
The stabilization of control systems is one of the most important properties of the systems and has been studied widely by many reseachers in control theory; (see, e.g., [1–11]) and the references therein. It is recognized that the Lyapunov function method serves as a main technique to reduce a given complicated system into a relatively simpler system and provides useful applications to control theory, but finding Lyapunov functions is still a difficult task (see, e.g., [1–3, 12, 13]). By contrast, many methods different from Lyapunov functions have been successfully applied to establish stabilizability results for discrete-time equations. For example, to the linear system

if the evolution operator  generated by
generated by  is stable, then the delay control system (1.1)-(1.2) is asymptotically stabilizable under appropiate conditions on
is stable, then the delay control system (1.1)-(1.2) is asymptotically stabilizable under appropiate conditions on  (see [4, 8, 14]). For infinite-dimensional control systems, the study of stabilizabilization is more complicated and requires sophisticated techniques from semigroup theory.
(see [4, 8, 14]). For infinite-dimensional control systems, the study of stabilizabilization is more complicated and requires sophisticated techniques from semigroup theory.
The concept of stabilizability has been developed and successfully applied in different settings (see, e.g., [9, 15, 16]). For example, finite- and infinite-dimensional discrete-time control systems have been studied extensively (see, e.g., [2, 5, 6, 10, 17–20]).
The stabilizability conditions obtained in this paper are derived by using the "freezing" technique (see, e.g., [21–23]) for perturbed systems of difference equations with slowly varying coefficients and do not involve either Lyapunov functions or stability assumptions on the associated evolution operator  . With more precision, the freezing technique can be described as follows. If
. With more precision, the freezing technique can be described as follows. If  is any fixed integer, then we can think of the autonomous system
is any fixed integer, then we can think of the autonomous system

as a particular case of the system (1.1), with its time dependence "frozen" at time  Thus, in this paper it is shown that if each frozen system is exponentially stabilizable and the rate of change of the coefficients of system (1.1) is small enough, then the nonautonomous system (1.1)-(1.2) is indeed exponentially stabilizable.
Thus, in this paper it is shown that if each frozen system is exponentially stabilizable and the rate of change of the coefficients of system (1.1) is small enough, then the nonautonomous system (1.1)-(1.2) is indeed exponentially stabilizable.
The purpose of this paper is to establish sufficient conditions for the global exponential feedback stabilizability of perturbed control systems with both time-varying and time-delayed states.
Our main contributions are as follows. By applying the "freezing" technique to the control system (1.1)-(1.2), we derive explicit stabilizability conditions, provided that the coefficients are slowly varying. Applications of the main results to control systems with many delays and nonlinear perturbations will also be established in this paper. This technique will allow us to avoid constructing the Lyapunov functions in some situations. For instance, it is worth noting that Niamsup and Phat [2] established sufficient stabilizability conditions for the zero solution of a discrete-time control system with many delays, under exponential growth assumptions on the corresponding transition matrix. By contrast, our approach does not involve any stability assumption on the transition matrix.
The paper is organized as follows. In Section 2 we introduce notations, definition, and some preliminary results. In Section 3, we give new sufficient conditions for the global exponential stabilizability of discrete-time systems with time-delayed states. Finally, as an application, we consider the global stabilization of the nonlinear control systems.
2. Preliminaries
In this paper we will use the following control law:

where  is a variable
is a variable  matrix.
matrix.
To formulate our results, let us introduce the following notation. Let  be a constant
be a constant  matrix and let
matrix and let  denote the eigenvalues of
denote the eigenvalues of  , including their multiplicities. Put
, including their multiplicities. Put

where  is the Hilbert-Schmidt (Frobenius) norm of
is the Hilbert-Schmidt (Frobenius) norm of  ; that is,
; that is, 
The following relation

is true, and will be useful to obtain some estimates in this work.
Theorem 2 A (11,Theorem 3.7).
For any  -matrix
-matrix  , the inequality
, the inequality

holds for every nonnegative integer  , where
, where  is the spectral radius of
is the spectral radius of  , and
, and  .
.
Remark 2.1.
In general, the problem of obtaining a precise estimate for the norm of matrix-valued and operator-valued functions has been regularly discussed in the literature, for example, see Gel'fond and Shilov [24] and Daleckii and Krein [25].
The following concepts of stability will be used in formulating the main results of the paper (see, e.g., [26]).
Definition 2.2.
The zero solution of system (1.4)–(1.2) is stable if for every  and every
and every  there is a number
there is a number  (depending on
(depending on  and
and  ) such that every solution
) such that every solution  of the system with
of the system with  for all
for all  , satisfies the condition
, satisfies the condition

Definition 2.3.
The zero solution of (1.4) is globally exponentially stable if there are constants  and
and  such that
such that

for any solution  of (1.4) with the initial conditions (1.2).
of (1.4) with the initial conditions (1.2).
Definition 2.4.
The pair  is said to be stabilizable for each
is said to be stabilizable for each  if there is a matrix
if there is a matrix  such that all the eigenvalues of the matrix
such that all the eigenvalues of the matrix  are located inside the unit disk for every fixed
are located inside the unit disk for every fixed  Namely,
Namely,

Remark 2.5.
The control  is a feedback control of the system.
is a feedback control of the system.
Definition 2.6.
System (1.1) is said to be globally exponentially stabilizable (at  ) by means of the feedback law (2.1) if there is a variable matrix
) by means of the feedback law (2.1) if there is a variable matrix  such that the zero solution of (1.4) is globally exponentially stable.
such that the zero solution of (1.4) is globally exponentially stable.
3. Main Results
Now, we are ready to establish the main results of the paper, which will be valid for the system (1.1)-(1.2) with slowly varying coefficients.
Consider in  the equation
the equation

subject to the initial conditions (1.2), where  is a given integer and
is a given integer and  is a variable
is a variable  matrix.
matrix.
Proposition 3.1.
Suppose that
-
(a)

-
(b)
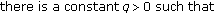
 (3.2)
(3.2) -
(c)

Then the zero solution of system (3.1)–(1.2) is globally exponentially stable. Moreover, any solution of (3.1) satisfies the inequality

where

Proof.
Rewrite (3.1) in the form

with a fixed nonnegative integer  . The variation of constants formula yields
. The variation of constants formula yields

Taking  , we have
, we have

Hence,

Thus,

Hence,

From this inequality we obtain

But, the right-hand side of this inequality does not depend on  . Thus, it follows that
. Thus, it follows that

This proves the global stability of the zero solution of (3.1)–(1.2).
To establish the global exponential stability of (3.1)–(1.2), we take the function

with  small enough, where
small enough, where  is a solution of (3.1).
is a solution of (3.1).
Substituting (3.13) in (3.1), we obtain

where

Applying the above reasoning to (3.14), according to inequality (3.3), it follows that  is a bounded function. Consequently, relation (3.13) implies the global exponential stability of the zero solution of system (3.1)–(1.2).
is a bounded function. Consequently, relation (3.13) implies the global exponential stability of the zero solution of system (3.1)–(1.2).
Computing the quantities  and
and  , defined by
, defined by

is not an easy task. However, in this section we will improve the estimates to these formulae.
Proposition 3.2.
Assume that (a) and (b) hold, and in addition

where  is the spectral radius of
is the spectral radius of  for each
for each  If
If

then the zero solution of system (3.1)–(1.2) is globally exponentially stable.
Proof.
Let us turn now to inequality (3.3). Firstly we will prove the inequality

where

Consider

By Theorem A, we have

But

Hence,

Proceeding in a similar way, we obtain

These relations yield inequality (3.19). Consequently,

where

Relation (3.26) proves the global stability of the zero solution of system (3.1)–(1.2). Establishing the exponential stability of this equation is enough to apply the same arguments of the Proposition 3.1.
Theorem 3.3.
Under the assumption (a), let  be stabilizable for each fixed
be stabilizable for each fixed  with respect to a matrix function
with respect to a matrix function  satisfying the following conditions:
satisfying the following conditions:
-
(i)

-
(ii)
 and
and -
(iii)

If,

then system (1.1)-(1.2) is globally exponentially stabilizable by means of the feedback law (2.1).
Proof.
Rewrite (1.4) in the form

where 
According to (i), (ii), and (iii), the conditions (b) and (3.17) hold. Furthermore, condition (3.28) assures the existence of a matrix function  such that condition (3.18) is fulfilled. Thus, from Proposition 3.2, the result follows.
such that condition (3.18) is fulfilled. Thus, from Proposition 3.2, the result follows.
Put

where the minimum is taken over all  matrices
matrices  satisfying (i), (ii), and (iii).
satisfying (i), (ii), and (iii).
Corollary 3.4.
Suppose that (a) holds, and the pair  is stabilizable for each fixed
is stabilizable for each fixed  If
If

then the system (1.1)-(1.2) is globally exponentially stabilizable by means of the feedback law (2.1).
Now, consider in  the discrete-time control system
the discrete-time control system

subject to the same initial conditions (1.2), where  and
and  are constant matrices. In addition, one assumes that the pair
are constant matrices. In addition, one assumes that the pair  is stabilizable, that is, there is a constant matrix
is stabilizable, that is, there is a constant matrix  such that all the eigenvalues of
such that all the eigenvalues of  are located inside the unit disk. Hence,
are located inside the unit disk. Hence,  In this case,
In this case,  and
and  Thus,
Thus,

Hence, Theorem 3.3 implies the following corollary.
Corollary 3.5.
Let  be a stabilizable pair of constant matrices, with respect to a constant matrix
be a stabilizable pair of constant matrices, with respect to a constant matrix  satisfying the condition
satisfying the condition

Then system (3.32)-(1.2), under condition (a), is globally exponentially stabilizable by means of the feedback law (2.1).
Example 3.6.
Consider the control system in  :
:

where  and
and  , subject to the initial conditions
, subject to the initial conditions

where  is a given function with values in
is a given function with values in  ,
,  are positive scalar-valued bounded sequences with the property
are positive scalar-valued bounded sequences with the property

and  are positive scalar-valued sequences with
are positive scalar-valued sequences with

In the present case, the pair  is controllable. Take
is controllable. Take

Then

where  and
and 
By inequality

it follows that

Assume that

Since  and
and  are constants, by (3.37) we have
are constants, by (3.37) we have  Hence, according to (3.28),
Hence, according to (3.28),

If  and
and  are small enough such that for some
are small enough such that for some  and
and  we have
we have  then by Theorem 3.3, system (3.35)-(3.36), under conditions (3.37) and (3.38), is globally exponentially stabilizable.
then by Theorem 3.3, system (3.35)-(3.36), under conditions (3.37) and (3.38), is globally exponentially stabilizable.
In the same way, Theorem 3.3 can be extended to the discrete-time control system with multiple delays


where  (
( ) are variable
) are variable  matrices,
matrices, 
Denote

Theorem 3.7.
Let  be stabilizable for each
be stabilizable for each  with respect to a matrix function
with respect to a matrix function  satisfying the conditions (i), (ii), and (iii). In addition, assume that
satisfying the conditions (i), (ii), and (iii). In addition, assume that

If

then system (3.45)-(3.46) is globally exponentially stabilizable by means of the feedback law (2.1). Moreover, any solution of (3.45)-(3.46) satisfies the inequality

As an application, one consider, the stabilization of the nonlinear discrete-time control system


where 
 is a given nonlinear function satisfying
is a given nonlinear function satisfying

for some positive numbers  and
and 
One recalls that nonlinear control system (3.51)-(3.52) is stabilizable by a feedback control  where
where  is a matrix, if the closed-loop system
is a matrix, if the closed-loop system

is asymptotically stable.
Theorem 3.8.
Under (3.53), let  be stabilizable for each
be stabilizable for each  with respect to a matrix function
with respect to a matrix function  satisfying conditions (i), (ii), and (iii). In addition, assume that
satisfying conditions (i), (ii), and (iii). In addition, assume that

If

then system (3.51)-(3.52) is globally exponentially stabilizable by means of the feedback law (2.1).
Proof.
Rewrite (3.54) in the form

where 
Thus, by reasoning as in Theorem 3.3, and using the estimates established in Proposition 3.2, the result follows.
References
Lakshmikantham V, Leela S, Martynyuk AA: Stability Analysis of Nonlinear Systems, Monographs and Textbooks in Pure and Applied Mathematics. Volume 125. Marcel Dekker, New York, NY, USA; 1989:xii+315.
Niamsup P, Phat VN: Asymptotic stability of nonlinear control systems described by difference equations with multiple delays. Electronic Journal of Differential Equations 2000,2000(11):1–17.
Sun YJ, Hsieh JG: Robust stabilization for a class of uncertain nonlinear systems with time-varying delay: Razumikhin-type approach. Journal of Optimization Theory and Applications 1998,98(1):161–173. 10.1023/A:1022645116123
Phat VN, Kiet TT: On the Lyapunov equation in Banach spaces and applications to control problems. International Journal of Mathematics and Mathematical Sciences 2002,29(3):155–166. 10.1155/S0161171202010840
Recht B, D'Andrea R: Distributed control of systems over discrete groups. IEEE Transactions on Automatic Control 2004,49(9):1446–1452. 10.1109/TAC.2004.834122
Sasu B, Sasu AL: Stability and stabilizability for linear systems of difference equations. Journal of Difference Equations and Applications 2004,10(12):1085–1105. 10.1080/10236190412331314178
Feliachi A, Thowsen A: Memoryless stabilization of linear delay-differential systems. IEEE Transactions on Automatic Control 1981,26(2):586–587. 10.1109/TAC.1981.1102653
Benabdallah A, Hammami MA: On the output feedback stability for non-linear uncertain control systems. International Journal of Control 2001,74(6):547–551. 10.1080/00207170010017383
Alabau F, Komornik V: Boundary observability, controllability, and stabilization of linear elastodynamic systems. SIAM Journal on Control and Optimization 1999,37(2):521–542. 10.1137/S0363012996313835
Boukas EK: State feedback stabilization of nonlinear discrete-time systems with time-varying time delay. Nonlinear Analysis: Theory, Methods & Applications 2007,66(6):1341–1350. 10.1016/j.na.2006.01.020
Bourlès H: Local -stability and local small gain theorem for discrete-time systems. IEEE Transactions on Automatic Control 1996,41(6):903–907. 10.1109/9.506248
Chukwu EN: Stability and Time-Optimal Control of Hereditary Systems, Mathematics in Science and Engineering. Volume 188. Academic Press, New York, NY, USA; 1992:xii+508.
Sontag ED: Asymptotic amplitudes and Cauchy gains: a small-gain principle and an application to inhibitory biological feedback. Systems & Control Letters 2002,47(2):167–179. 10.1016/S0167-6911(02)00191-3
Trinh H, Aldeen M: On robustness and stabilization of linear systems with delayed nonlinear perturbations. IEEE Transactions on Automatic Control 1997,42(7):1005–1007. 10.1109/9.599983
Gaĭshun IV: Controllability and stabilizability of discrete systems in a function space on a commutative semigroup. Difference Equations 2004,40(6):873–882.
Megan M, Sasu AL, Sasu B: Stabilizability and controllability of systems associated to linear skew-product semiflows. Revista Matemática Complutense 2002,15(2):599–618.
Gil MI, Medina R: The freezing method for linear difference equations. Journal of Difference Equations and Applications 2002,8(5):485–494. 10.1080/10236190290017478
Jiang Z-P, Lin Y, Wang Y: Nonlinear small-gain theorems for discrete-time feedback systems and applications. Automatica 2004,40(12):2129–2136.
Karafyllis I: Non-uniform in time robust global asymptotic output stability for discrete-time systems. International Journal of Robust and Nonlinear Control 2006,16(4):191–214. 10.1002/rnc.1037
Karafyllis I: Non-uniform robust global asymptotic stability for discrete-time systems and applications to numerical analysis. IMA Journal of Mathematical Control and Information 2006,23(1):11–41.
Bylov BF, Grobman BM, Nemickii VV, Vinograd RE: The Theory of Lyapunov Exponents. Nauka, Moscow, Russia; 1966.
Shahruz SM, Schwartz AL: An approximate solution for linear boundary-value problems with slowly varying coefficients. Applied Mathematics and Computation 1994,60(2–3):285–298. 10.1016/0096-3003(94)90110-4
Vinograd RE: An improved estimate in the method of freezing. Proceedings of the American Mathematical Society 1983,89(1):125–129. 10.1090/S0002-9939-1983-0706524-1
Gel'fand IM, Shilov GE: Some Questions of Differential Equations. Nauka, Moscow, Russia; 1958.
Daleckii Yul, Krein MG: Stability of Solutions of Differential Equations in Banach Spaces. American Mathematical Society, Providence, RI, USA; 1971.
Berezansky L, Braverman E: Exponential stability of difference equations with several delays: recursive approach. Advances in Difference Equations 2009, 2009:-13.
Acknowledgment
This research was supported by Fondecyt Chile under Grant no. 1.070.980.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rigoberto, M. Stabilization of Discrete-Time Control Systems with Multiple State Delays. Adv Differ Equ 2009, 240707 (2009). https://doi.org/10.1155/2009/240707
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/240707

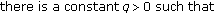



 and
and