- Research Article
- Open access
- Published:
Existence Results for Higher-Order Boundary Value Problems on Time Scales
Advances in Difference Equations volume 2009, Article number: 209707 (2009)
Abstract
By using the fixed-point index theorem, we consider the existence of positive solutions for the following nonlinear higher-order four-point singular boundary value problem on time scales  ,
,  ;
;  ,
,  ;
;  ,
,  ;
;  ,
,  , where
, where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  is rd-continuous.
is rd-continuous.
1. Introduction
Time scales and time-scale notationare introduced well in the fundamental texts by Bohner and Peterson [1, 2], respectively, as important corollaries. In, the recent years, many authors have paid much attention to the study of boundary value problems on time scales (see, e.g., [3–17]). In particular, we would like to mention some results of Anderson et al. [3, 5, 6, 14, 16], DaCunha et al. [4], and Agarwal and O'Regan [7], which motivate us to consider our problem.
In [3], Anderson and Karaca discussed the dynamic equation on time scales

and the eigenvalue problem

with the same boundary conditions where  is a positive parameter. They obtained some results for the existence of positive solutions by using the Krasnoselskii, the Schauder, and the Avery-Henderson fixed-point theorem.
is a positive parameter. They obtained some results for the existence of positive solutions by using the Krasnoselskii, the Schauder, and the Avery-Henderson fixed-point theorem.
In [4], by using the Gatica-Oliker-Waltman fixed-point theorem, DaCunha, Davis, and Singh proved the existence of a positive solution for the three-point boundary value problem on a time scale  given by
given by

where  is fixed, and
is fixed, and  is singular at
is singular at  and possibly at
and possibly at  .
.
Anderson et al. [5] gave a detailed presentation for the following higher-order self-adjoint boundary value problem on time scales:

and got many excellent results.
In related papers, Sun [11] considered the following third-order two-point boundary value problem on time scales:

where  and
and  . Some existence criteria of solution and positive solution are established by using the Leray-Schauder fixed point theorem.
. Some existence criteria of solution and positive solution are established by using the Leray-Schauder fixed point theorem.
In this paper, we consider the existence of positive solutions for the following higher-order four-point singular boundary value problem (BVP) on time scales


where  ,
, 
 , and
, and  is rd-continuous. In the rest of the paper, we make the following assumptions:
is rd-continuous. In the rest of the paper, we make the following assumptions:
()
() .
.
In this paper, by constructing one integral equation which is equivalent to the BVP (1.6) and (1.7), we study the existence of positive solutions. Our main tool of this paper is the following fixed-point index theorem.
Theorem 1.1 ([18]).
Suppose  is a real Banach space,
is a real Banach space,  is a cone, let
is a cone, let  . Let operator
. Let operator 
 be completely continuous and satisfy
be completely continuous and satisfy  . Then
. Then
(i)if  , then
, then 
(ii)if  , then
, then  .
.
The outline of the paper is as follows. In Section 2, for the convenience of the reader we give some definitions and theorems which can be found in the references, and we present some lemmas in order to prove our main results. Section 3 is developed in order to present and prove our main results. In Section 4 we present some examples to illustrate our results.
2. Preliminaries and Lemmas
For convenience, we list the following definitions which can be found in [1, 2, 9, 14, 17]. A time scale  is a nonempty closed subset of real numbers
is a nonempty closed subset of real numbers  . For
. For  and
and  , define the forward jump operator
, define the forward jump operator  and backward jump operator
and backward jump operator  , respectively, by
, respectively, by

for all  . If
. If  ,
,  is said to be right scattered, and if
is said to be right scattered, and if  ,
,  is said to be left scattered; if
is said to be left scattered; if  ,
,  is said to be right dense, and if
is said to be right dense, and if  ,
,  is said to be left dense. If
is said to be left dense. If  has a right scattered minimum
has a right scattered minimum  , define
, define  ; otherwise set
; otherwise set  . If
. If  has a left scattered maximum
has a left scattered maximum  , define
, define  ; otherwise set
; otherwise set  . In this general time-scale setting,
. In this general time-scale setting,  represents the delta (or Hilger) derivative [13, Definition 1.10],
represents the delta (or Hilger) derivative [13, Definition 1.10],

where  is the forward jump operator,
is the forward jump operator,  is the forward graininess function, and
is the forward graininess function, and  is abbreviated as
is abbreviated as  . In particular, if
. In particular, if  , then
, then  and
and  , while if
, while if  for any
for any  , then
, then  and
and

A function  is right-dense continuous provided that it is continuous at each right-dense point
is right-dense continuous provided that it is continuous at each right-dense point  (a point where
(a point where  ) and has a left-sided limit at each left-dense point
) and has a left-sided limit at each left-dense point  . The set of right-dense continuous functions on
. The set of right-dense continuous functions on  is denoted by
is denoted by  . It can be shown that any right-dense continuous function
. It can be shown that any right-dense continuous function  has an antiderivative (a function
has an antiderivative (a function  with the property
with the property  for all
for all  ). Then the Cauchy delta integral of
). Then the Cauchy delta integral of  is defined by
is defined by

where  is an antiderivative of
is an antiderivative of  on
on  . For example, if
. For example, if  , then
, then

and if  , then
, then

Throughout we assume that  are points in
are points in  , and define the time-scale interval
, and define the time-scale interval  . In this paper, we also need the the following theorem which can be found in [1].
. In this paper, we also need the the following theorem which can be found in [1].
Theorem 2.1.
If  and
and  then
then

In this paper, let

Then  is a Banach space with the norm
is a Banach space with the norm  . Define a cone
. Define a cone  by
by

Obviously,  is a cone in
is a cone in  . Set
. Set  . If
. If  on
on  then we say
then we say  is concave on
is concave on  We can get the following.
We can get the following.
Lemma 2.2.
Suppose condition  holds. Then there exists a constant
holds. Then there exists a constant  satisfies
satisfies

Furthermore, the function

is a positive continuous function on  , therefore
, therefore  has minimum on
has minimum on  . Then there exists
. Then there exists  such that
such that  .
.
Lemma 2.3.
Let  and
and  in Lemma 2.2. Then
in Lemma 2.2. Then

Proof.
Suppose  .
.
We will discuss it from three perspectives.
(i) . It follows from the concavity of
. It follows from the concavity of  that
that

then

which means  .
.
(ii) . If
. If  , we have
, we have

then

If  , we have
, we have

then

and this means  .
.
(iii) . Similarly, we have
. Similarly, we have

then

which means  .
.
From the above, we know  . The proof is complete.
. The proof is complete.
Lemma 2.4.
Suppose that conditions  hold, then
hold, then  is a solution of boundary value problem (1.6), (1.7) if and only if
is a solution of boundary value problem (1.6), (1.7) if and only if  is a solution of the following integral equation:
is a solution of the following integral equation:

where

Proof.
Necessity. By the equation of the boundary condition, we see that  , then there exists a constant
, then there exists a constant  such that
such that  . Firstly, by delta integrating the equation of the problems (1.6) on
. Firstly, by delta integrating the equation of the problems (1.6) on  , we have
, we have

thus

By  and the boundary condition (1.7), let
and the boundary condition (1.7), let  on (2.23), we have
on (2.23), we have

By the equation of the boundary condition (1.7), we get

then

Secondly, by (2.24) and let  on (2.24), we have
on (2.24), we have

Then

Then by delta integrating (2.29) for  times on
times on  , we have
, we have

Similarly, for  , by delta integrating the equation of problems (1.6) on
, by delta integrating the equation of problems (1.6) on  , we have
, we have

Therefore, for any  ,
,  can be expressed as the equation
can be expressed as the equation

where  is expressed as (2.22).
is expressed as (2.22).
Sufficiency. Suppose that

then by (2.22), we have

So,

which imply that (1.6) holds. Furthermore, by letting  and
and  on (2.22) and (2.34), we can obtain the boundary value equations of (1.7). The proof is complete.
on (2.22) and (2.34), we can obtain the boundary value equations of (1.7). The proof is complete.
Now, we define a mapping  given by
given by

where  is given by (2.22).
is given by (2.22).
Lemma 2.5.
Suppose that conditions  hold, the solution
hold, the solution  of problem (1.6), (1.7) satisfies
of problem (1.6), (1.7) satisfies

and for  in Lemma 2.2, one has
in Lemma 2.2, one has

Proof.
If  is the solution of (1.6), (1.7), then
is the solution of (1.6), (1.7), then  is a concave function, and
is a concave function, and  , thus we have
, thus we have

that is,

By Lemma 2.3, for  , we have
, we have

then  . The proof is complete.
. The proof is complete.
Lemma 2.6.
 is completely continuous.
is completely continuous.
Proof.
Because

is continuous, decreasing on  and satisfies
and satisfies  . Then,
. Then,  for each
for each  and
and  . This shows that
. This shows that  . Furthermore, it is easy to check that
. Furthermore, it is easy to check that  is completely continuous by Arzela-ascoli Theorem.
is completely continuous by Arzela-ascoli Theorem.
For convenience, we set

where  is the constant from Lemma 2.2. By Lemma 2.5, we can also set
is the constant from Lemma 2.2. By Lemma 2.5, we can also set

3. The Existence of Positive Solution
Theorem 3.1.
Suppose that conditions ( ), (
), ( ) hold. Assume that
) hold. Assume that  also satisfies
also satisfies


where 
Then, the boundary value problem (1.6), (1.7) has a solution  such that
such that  lies between
lies between  and
and  .
.
Theorem 3.2.
Suppose that conditions ( ), (
), ( ) hold. Assume that
) hold. Assume that  also satisfies
also satisfies


Then, the boundary value problem (1.6), (1.7) has a solution  such that
such that  lies between
lies between  and
and  .
.
Theorem 3.3.
Suppose that conditions ( ), (
), ( ) hold. Assume that
) hold. Assume that  also satisfies
also satisfies
()
()
Then, the boundary value problem (1.6), (1.7) has a solution  such that
such that  lies between
lies between  and
and  .
.
Proof of Theorem 3.1.
Without loss of generality, we suppose that  . For any
. For any  , by Lemma 2.3, we have
, by Lemma 2.3, we have

We define two open subsets  and
and  of
of  :
:

For any  , by (3.1) we have
, by (3.1) we have

For  and
and  , we will discuss it from three perspectives.
, we will discuss it from three perspectives.
(i)If  , thus for
, thus for  , by (
, by ( ) and Lemma 2.4, we have
) and Lemma 2.4, we have

-
(ii)
If
 , thus for
, thus for 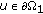 , by (
, by (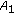 ) and Lemma 2.4, we have
) and Lemma 2.4, we have

-
(iii)
If
 , thus for
, thus for  , by (
, by ( ) and Lemma 2.4, we have
) and Lemma 2.4, we have

Therefore, no matter under which condition, we all have

Then by Theorem 2.1, we have

On the other hand, for  , we have
, we have  ; by (
; by ( ) we know
) we know

thus

Then, by Theorem 2.1, we get

Therefore, by (3.8), (3.11),  , we have
, we have

Then operator  has a fixed point
has a fixed point  , and
, and  . Then the proof of Theorem 3.1 is complete .
. Then the proof of Theorem 3.1 is complete .
Proof of Theorem 3.2.
First, by  , for
, for  , there exists an adequately small positive number
, there exists an adequately small positive number  , as
, as  , we have
, we have

Then let  , thus by (3.13)
, thus by (3.13)

So condition ( ) holds. Next, by condition (
) holds. Next, by condition ( ),
),  , then for
, then for  , there exists an appropriately big positive number
, there exists an appropriately big positive number  , as
, as  , we have
, we have

Let  , thus by (3.15), condition (
, thus by (3.15), condition ( ) holds. Therefore by Theorem 3.1 we know that the results of Theorem 3.2 hold. The proof of Theorem 3.2 is complete.
) holds. Therefore by Theorem 3.1 we know that the results of Theorem 3.2 hold. The proof of Theorem 3.2 is complete.
Proof of Theorem 3.3.
Firstly, by condition ( ),
),  , then for
, then for  , there exists an adequately small positive number
, there exists an adequately small positive number  , as
, as  , we have
, we have

thus when  , we have
, we have

Let  , so by (3.17), condition (
, so by (3.17), condition ( ) holds.
) holds.
Secondly, by condition ( ),
),  , then for
, then for  , there exists a suitably big positive number
, there exists a suitably big positive number  , as
, as  , we have
, we have

If  is unbounded, by the continuity of
is unbounded, by the continuity of  on
on  , then there exist a constant
, then there exist a constant  , and a point
, and a point  such that
such that

Thus, by  we know
we know

Choose  . Then, we have
. Then, we have

If  is bounded, we suppose
is bounded, we suppose  , there exists an appropriately big positive number
, there exists an appropriately big positive number  , then choose
, then choose  , we have
, we have

Therefore, condition ( ) holds. Thus, by Theorem 3.1, we know that the result of Theorem 3.3 holds. The proof of Theorem 3.3 is complete.
) holds. Thus, by Theorem 3.1, we know that the result of Theorem 3.3 holds. The proof of Theorem 3.3 is complete.
4. Application
In this section, in order to illustrate our results, we consider the following examples.
Example 4.1.
Consider the following boundary value problem on the specific time scale :
:

where

and  is the constant defined in Lemma 2.2,
is the constant defined in Lemma 2.2,

Then obviously

By Theorem 2.1, we have

so conditions ( ),
),  hold.
hold.
By simple calculations, we have

then  , that is,
, that is,  , so condition
, so condition  holds.
holds.
For  , it is easy to see that
, it is easy to see that

so condition  holds. Then by Theorem 3.2, BVP (4.1) has at least one positive solution.
holds. Then by Theorem 3.2, BVP (4.1) has at least one positive solution.
Example 4.2.
Consider the following boundary value problem on the specific time scale  .
.

where

and  is the constant from Lemma 2.2,
is the constant from Lemma 2.2,

Then obviously

By Theorem 2.1, we have

so conditions ( ),
),  hold. By simple calculations, we have
hold. By simple calculations, we have

then  , that is,
, that is,  , so condition
, so condition  holds.
holds.
For  , it is easy to see that
, it is easy to see that

then condition  holds. Thus by Theorem 3.3, BVP (4.8) has at least one positive solution.
holds. Thus by Theorem 3.3, BVP (4.8) has at least one positive solution.
References
Bohner M, Peterson A: Dynamic Equations on Time Scales, An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Anderson DR, Karaca IY: Higher-order three-point boundary value problem on time scales. Computers & Mathematics with Applications 2008,56(9):2429–2443. 10.1016/j.camwa.2008.05.018
DaCunha JJ, Davis JM, Singh PK: Existence results for singular three point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004,295(2):378–391. 10.1016/j.jmaa.2004.02.049
Anderson DR, Guseinov GSh, Hoffacker J: Higher-order self-adjoint boundary-value problems on time scales. Journal of Computational and Applied Mathematics 2006,194(2):309–342. 10.1016/j.cam.2005.07.020
Anderson DR, Avery R, Davis J, Henderson J, Yin W: Positive solutions of boundary value problems. In Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:189–249.
Agarwal RP, O'Regan D: Nonlinear boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2001,44(4):527–535. 10.1016/S0362-546X(99)00290-4
Kaufmann ER: Positive solutions of a three-point boundary-value problem on a time scale. Electronic Journal of Differential Equations 2003, (82):1–11.
Atici FM, Guseinov GSh: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002,141(1–2):75–99. 10.1016/S0377-0427(01)00437-X
Boey KL, Wong PJY: Existence of triple positive solutions of two-point right focal boundary value problems on time scales. Computers & Mathematics with Applications 2005,50(10–12):1603–1620.
Sun J-P: Existence of solution and positive solution of BVP for nonlinear third-order dynamic equation. Nonlinear Analysis: Theory, Methods & Applications 2006,64(3):629–636. 10.1016/j.na.2005.04.046
Benchohra M, Henderson J, Ntouyas SK: Eigenvalue problems for systems of nonlinear boundary value problems on time scales. Advances in Difference Equations 2007, 2007:-10.
Agarwal RP, Otero-Espinar V, Perera K, Vivero DR: Multiple positive solutions in the sense of distributions of singular BVPs on time scales and an application to Emden-Fowler equations. Advances in Difference Equations 2008, 2008:-13.
Anderson DR: Oscillation and nonoscillation criteria for two-dimensional time-scale systems of first-order nonlinear dynamic equations. Electronic Journal of Differential Equations 2009,2009(24):13. Article ID 796851.
Bohner M, Luo H: Singular second-order multipoint dynamic boundary value problems with mixed derivatives. Advances in Difference Equations 2006, 2006:-15.
Anderson DR, Ma R: Second-order -point eigenvalue problems on time scales. Advances in Difference Equations 2006, 2006:-17.
Henderson J, Peterson A, Tisdell CC: On the existence and uniqueness of solutions to boundary value problems on time scales. Advances in Difference Equations 2004,2004(2):93–109. 10.1155/S1687183904308071
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgment
The authors would like to thank the anonymous referee for his/her valuable suggestions, which have greatly improved this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, J., Sang, Y. Existence Results for Higher-Order Boundary Value Problems on Time Scales. Adv Differ Equ 2009, 209707 (2009). https://doi.org/10.1155/2009/209707
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/209707
 , thus for
, thus for 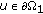 , by (
, by (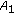 ) and Lemma 2.4, we have
) and Lemma 2.4, we have , thus for
, thus for  , by (
, by ( ) and Lemma 2.4, we have
) and Lemma 2.4, we have