- Research Article
- Open access
- Published:
The Existence of Positive Solutions for Third-Order  -Laplacian
-Laplacian 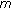 -Point Boundary Value Problems with Sign Changing Nonlinearity on Time Scales
-Point Boundary Value Problems with Sign Changing Nonlinearity on Time Scales
Advances in Difference Equations volume 2009, Article number: 169321 (2009)
Abstract
We study the following third-order  -Laplacian
-Laplacian  -point boundary value problems on time scales
-point boundary value problems on time scales  ,
,  ,
,  ,
,  ,
,  , where
, where  is
is  -Laplacian operator, that is,
-Laplacian operator, that is,  ,
,  ,
,  ,
,  . We obtain the existence of positive solutions by using fixed-point theorem in cones. In particular, the nonlinear term
. We obtain the existence of positive solutions by using fixed-point theorem in cones. In particular, the nonlinear term  is allowed to change sign. The conclusions in this paper essentially extend and improve the known results.
is allowed to change sign. The conclusions in this paper essentially extend and improve the known results.
1. Introduction
The theory of time scales was initiated by Hilger [1] as a mean of unifying and extending theories from differential and difference equations. The study of time scales has lead to several important applications in the study of insect population models, neural networks, heat transfer, and epidemic models, see, for example [2–6]. Recently, the boundary value problems with  -Laplacian operator have also been discussed extensively in literature; for example, see [7–18]. However, to the best of our knowledge, there are not many results concerning the higher-order
-Laplacian operator have also been discussed extensively in literature; for example, see [7–18]. However, to the best of our knowledge, there are not many results concerning the higher-order  -Laplacian mutilpoint boundary value problem on time scales.
-Laplacian mutilpoint boundary value problem on time scales.
A time scale  is a nonempty closed subset of
is a nonempty closed subset of  . We make the blanket assumption that
. We make the blanket assumption that  are points in
are points in  . By an interval
. By an interval  , we always mean the intersection of the real interval
, we always mean the intersection of the real interval  with the given time scale; that is
with the given time scale; that is  .
.
In [19], Anderson considered the following third-order nonlinear boundary value problem (BVP):

author studied the existence of solutions for the nonlinear boundary value problem by using Krasnoselskii's fixed point theorem and Leggett and Williams fixed point theorem, respectively.
In [9, 10], He considered the existence of positive solutions of the  -Laplacian dynamic equations on time scales
-Laplacian dynamic equations on time scales

satisfying the boundary conditions

or

where  . He obtained the existence of at least double and triple positive solutions of the problems by using a new double fixed point theorem and triple fixed point theorem, respectively.
. He obtained the existence of at least double and triple positive solutions of the problems by using a new double fixed point theorem and triple fixed point theorem, respectively.
In [18], Zhou and Ma firstly studied the existence and iteration of positive solutions for the following third-order generalized right-focal boundary value problem with  -Laplacian operator
-Laplacian operator

They established a corresponding iterative scheme for the problem by using the monotone iterative technique.
All the above works were done under the assumption that the nonlinear term is nonnegative. The key conditions used in the above papers ensure that positive solution is concave down. If the nonlinearity is negative somewhere, then the solution needs no longer to be concave down. As a result, it is difficult to find positive solutions of the  -Laplacian equation when the nonlinearity changes sign. In particular, little work has been done on the existence of positive solutions for higher order
-Laplacian equation when the nonlinearity changes sign. In particular, little work has been done on the existence of positive solutions for higher order  -Laplacian
-Laplacian  -point boundary value problems with nonlinearity
-point boundary value problems with nonlinearity  being nonnegative on time scales. Therefore, it is a natural problem to consider the existence of positive solution for higher order
being nonnegative on time scales. Therefore, it is a natural problem to consider the existence of positive solution for higher order  -Laplacian equations with sign changing nonlinearity on time scales. This paper attempts to fill this gap in literature.
-Laplacian equations with sign changing nonlinearity on time scales. This paper attempts to fill this gap in literature.
In this paper, by using different method, we are concerned with the existence of positive solutions for the following third-order  -Laplacian
-Laplacian  -point boundary value problems on time scales:
-point boundary value problems on time scales:

where  is
is  -Laplacian operator, that is,
-Laplacian operator, that is,  ,
,  ,
,  and
and  ,
,  ,
,  ,
,  satisfy
satisfy

 ,
,  ,
,  ,
,  ;
;
 is continuous,
is continuous,  , and there exists
, and there exists  such that
such that  .
.
2. Preliminaries and Lemmas
For convenience, we list the following definitions which can be found in [1–5].
Definition 2.1.
A time scale  is a nonempty closed subset of real numbers
is a nonempty closed subset of real numbers  . For
. For  and
and  , define the forward jump operator
, define the forward jump operator  and backward jump operator
and backward jump operator  , respectively, by
, respectively, by

for all  . If
. If  ,
,  is said to be right scattered, if
is said to be right scattered, if  ,
,  is said to be left scattered; if
is said to be left scattered; if  ,
,  is said to be right dense, and if
is said to be right dense, and if  ,
,  is said to be left dense. If
is said to be left dense. If  has a right scattered minimum
has a right scattered minimum  , define
, define  ; otherwise set
; otherwise set  . If
. If  has a left scattered maximum
has a left scattered maximum  , define
, define  ; otherwise set
; otherwise set  .
.
Definition 2.2.
For  and
and  , the delta derivative of
, the delta derivative of  at the point
at the point  is defined to be the number
is defined to be the number  (provided that it exists), with the property that for each
(provided that it exists), with the property that for each  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

for all  .
.
For  and
and  , the nabla derivative of
, the nabla derivative of  at
at  , denoted by
, denoted by  (provided it exists) with the property that for each
(provided it exists) with the property that for each  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

for all  .
.
Definition 2.3.
A function  is left-dense continuous (i.e.,
is left-dense continuous (i.e.,  -continuous), if
-continuous), if  is continuous at each left-dense point in
is continuous at each left-dense point in  and its right-sided limit exists at each right-dense point in
and its right-sided limit exists at each right-dense point in  .
.
Definition 2.4.
If  , then we define the delta integral by
, then we define the delta integral by

If  , then we define the nabla integral by
, then we define the nabla integral by

Lemma 2.5.
If condition  holds, then for
holds, then for  , the boundary value problem (BVP)
, the boundary value problem (BVP)

has the unique solution

Proof.
By caculating, we can easily get (2.7). So we omit it.
Lemma 2.6.
If condition  holds, then for
holds, then for  , the boundary value problem (BVP)
, the boundary value problem (BVP)

has the unique solution

where  .
.
Proof.
Integrating both sides of equation in (2.8) on  , we have
, we have

So,

By boundary value condition  , we have
, we have

By (2.10) and (2.12) we know

This together with Lemma 2.5 implies that

where  . The proof is complete.
. The proof is complete.
Lemma 2.7.
Let condition  holds If
holds If  and
and  , then the unique solution
, then the unique solution  of (2.8) satisfies
of (2.8) satisfies

Proof.
By  , we can know that the graph of
, we can know that the graph of  is concave down on
is concave down on  , and
, and  is nonincreasing on
is nonincreasing on  . This together with the assumption that the boundary condition
. This together with the assumption that the boundary condition  implies that
implies that  for
for  . This implies that
. This implies that

So we only prove  By condition
By condition  we have
we have

The proof is completed.
Lemma 2.8.
Let condition  hold. If
hold. If  and
and  , then the unique positive solution
, then the unique positive solution  of (BVP) (2.8) satisfies
of (BVP) (2.8) satisfies

where  ,
,  .
.
Proof.
By  , we can know that the graph of
, we can know that the graph of  is concave down on
is concave down on  , and
, and  is nonincreasing on
is nonincreasing on  . This together with the assumption that the boundary condition
. This together with the assumption that the boundary condition  implies that
implies that  for
for  . This implies that
. This implies that

For all  , we have from the concavity of
, we have from the concavity of  that
that

that is,

This together with the boundary condition  implies that
implies that

This completes the proof.
Let  be endowed with the ordering
be endowed with the ordering  if
if  for all
for all  and
and  is defined as usual by maximum norm. Clearly, it follows that
is defined as usual by maximum norm. Clearly, it follows that  is a Banach space.
is a Banach space.
For the convenience, let

We define two cones by

where  ,
,  is defined in Lemma 2.8 and
is defined in Lemma 2.8 and

Define the operators  and
and  by setting
by setting

where  ,
,

where  ,
,  , and
, and  . Obviously,
. Obviously,  is a solution of the BVP(1.6) if and only if
is a solution of the BVP(1.6) if and only if  is a fixed point of operator
is a fixed point of operator  .
.
Lemma 2.9.
 is completely continuous.
is completely continuous.
Proof.
It is easy to see that  by
by  and Lemma 2.8. By Arzela-Ascoli theorem and Lebesgue dominated convergence theorem, we can easily prove that operator
and Lemma 2.8. By Arzela-Ascoli theorem and Lebesgue dominated convergence theorem, we can easily prove that operator  is completely continuous.
is completely continuous.
Let  be a cone in a Banach space
be a cone in a Banach space  . Let
. Let  be an open bounded subset of
be an open bounded subset of  with
with  and
and  . Assume that
. Assume that  is a compact map such that
is a compact map such that  for
for  . Then the following results hold.
. Then the following results hold.
(1)If  ,
,  , then
, then  .
.
(2)If there exists  such that
such that  for all
for all  and all
and all  , then
, then  .
.
(3)Let  be open in
be open in  such that
such that  . If
. If  and
and  , then
, then  has a fixed point in
has a fixed point in  . The same result holds if
. The same result holds if  and
and  , where
, where  denotes fixed point index.
denotes fixed point index.
We define

Lemma 2.11 (see [20]).
 defined above has the following properties:
defined above has the following properties:
(a)
(b) is open relative to K;
is open relative to K;
(c) if and only if
if and only if 
(d)if  , then
, then  for
for  .
.
For the convenience, we introduce the following notations:

Remark 2.12.
By  we can know that
we can know that  ,
, 
Lemma 2.13.
If  satisfies the following condition :
satisfies the following condition :

then

Proof.
For  , then from (2.30) we have
, then from (2.30) we have

So that

Therefore,

This implies that  for
for  . Hence by Lemma 2.10(1) it follows that
. Hence by Lemma 2.10(1) it follows that  .
.
Lemma 2.14.
If  satisfies the following condition:
satisfies the following condition:

then

Proof.
Let  for
for  . Then
. Then  . We claim that
. We claim that

In fact, if not, there exist  and
and  such that
such that  . By
. By  , we have
, we have

So that

For  , then
, then

This together with Lemma 2.11(c) implies that

a contradiction. Hence by Lemma 2.10(2) it follows that  .
.
3. Main Results
We now give our results on the existence of positive solutions of BVP (1.6).
Theorem 3.1.
Suppose that conditions  and
and  hold, and assume that one of the following conditions holds.
hold, and assume that one of the following conditions holds.
There exist  with
with  such that
such that
(i) ,
,  ;
;
(ii) ,
,  , moreover
, moreover  ,
,  .
.
There exist  with
with  such that
such that
(i) ,
,  ;
;
(ii) ,
,  .
.
Then, the BVP (1.6) has at least one positive solution.
Proof.
Assume that  holds, we show that
holds, we show that  has a fixed point
has a fixed point  in
in  . By
. By  and Lemma 2.13, we have that
and Lemma 2.13, we have that

By  and Lemma 2.14, we have that
and Lemma 2.14, we have that

By Lemma 2.11(a) and  , we have
, we have  . It follows from Lemma 2.10(3) that
. It follows from Lemma 2.10(3) that  has a fixed point
has a fixed point  in
in  . Clearly,
. Clearly,

which implies that  ,
,  . By condition
. By condition  (ii), we have
(ii), we have  ,
,  , that is,
, that is,  . Hence,
. Hence,

This means that  is a fixed point of operator
is a fixed point of operator  .
.
When condition  holds, by
holds, by  and Lemma 2.13, we have that
and Lemma 2.13, we have that

By  and Lemma 2.14, we have that
and Lemma 2.14, we have that

By Lemma 2.11(a) and  , we have
, we have  . It follows from Lemma 2.10(3) that
. It follows from Lemma 2.10(3) that  has a fixed point
has a fixed point  in
in  . Obviously,
. Obviously,

which implies that  ,
,  . By condition
. By condition  (ii), we have
(ii), we have  ,
,  , that is,
, that is,  . Hence,
. Hence,

This means that  is a fixed point of operator
is a fixed point of operator  . Therefore, the BVP (1.6) has at least one positive solution.
. Therefore, the BVP (1.6) has at least one positive solution.
Theorem 3.2.
Assume that conditions  and
and  hold, and suppose that one of the following conditions holds.
hold, and suppose that one of the following conditions holds.
There exist  , and
, and  with
with  , and
, and  such that
such that
(i) ,
,  ;
;
(ii) ,
,  , moreover
, moreover  ,
,  ,
, 
 ;
;
(iii) ,
,  .
.
There exist  , and
, and  with
with  such that
such that
(i) ,
,  ;
;
(ii) ,
,  ,
,  ,
, ;
;
(iii) ,
,  , moreover,
, moreover,  ,
,  .
.
Then, the BVP (1.6) has at least two positive solutions.
Proof.
Assume that condition  holds, we show that
holds, we show that  has a fixed point
has a fixed point  either in
either in  or in
or in  . If
. If  for
for  . by Lemmas 2.13 and 2.14, we have that
. by Lemmas 2.13 and 2.14, we have that

By Lemma 2.11(a) and  , we have
, we have  . It follows from Lemma 2.10(3) that
. It follows from Lemma 2.10(3) that  has a fixed point
has a fixed point  in
in  . Similarly,
. Similarly,  has a fixed point
has a fixed point  in
in  . Clearly,
. Clearly,

which implies that  ,
,  . By condition
. By condition  (ii), we have
(ii), we have  ,
,  , that is,
, that is,  . Hence,
. Hence,

This means that  is a fixed point of operator
is a fixed point of operator  . On the other hand, from
. On the other hand, from  and Lemma 2.11(a), we have
and Lemma 2.11(a), we have  . Clearly,
. Clearly,

which implies that  . By
. By  and condition
and condition  (ii), we have
(ii), we have  , that is,
, that is,  . Hence,
. Hence,

This means that  is a fixed point of operator
is a fixed point of operator  . Then, the BVP (1.6) has at least two positive solutions.
. Then, the BVP (1.6) has at least two positive solutions.
When condition  holds, the proof is similar to the above, and so we omit it here.
holds, the proof is similar to the above, and so we omit it here.
4. An Example
In the section, we present some simple examples to explain our results.
Example 4.1.
Let  ,
,  . Consider the following three-point boundary value problem with
. Consider the following three-point boundary value problem with  -Laplacian
-Laplacian

where  ,
,  ,
,  ,
,  ,
,  .
.
By computing, we can know  ,
,  ,
,  ,
,  . Obviously,
. Obviously,  ,
,  .
.
Let  ,
,  , then
, then  . We define a sign changing nonlinearity as follows:
. We define a sign changing nonlinearity as follows:

Then, by the definition of  we have
we have
(i) ,
,  ;
;
(ii) ,
,  , moreover
, moreover  ,
,  .
.
So condition  holds, and by Theorem 3.1, BVP (4.1) has at least one positive solution.
holds, and by Theorem 3.1, BVP (4.1) has at least one positive solution.
References
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1–2):18–56.
Agarwal RP, O'Regan D: Nonlinear boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2001,44(4):527–535. 10.1016/S0362-546X(99)00290-4
Atici FM, Guseinov GSh: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002,141(1–2):75–99. 10.1016/S0377-0427(01)00437-X
Sun H-R, Li W-T: Positive solutions for nonlinear three-point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004,299(2):508–524. 10.1016/j.jmaa.2004.03.079
Bohner M, Peterso A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Sun HR, Li WT: Positive solutions for nonlinear -point boundary value problems on time scales. Acta Mathematica Sinica 2006,49(2):369–380.
Sun H-R, Li W-T: Existence theory for positive solutions to one-dimensional -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217–248. 10.1016/j.jde.2007.06.004
Su Y-H, Li W-T, Sun H-R: Triple positive pseudo-symmetric solutions of three-point BVPs for -Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1442–1452.
He Z: Double positive solutions of three-point boundary value problems for -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304–315. 10.1016/j.cam.2004.12.012
He Z, Jiang X: Triple positive solutions of boundary value problems for -Laplacian dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2006,321(2):911–920. 10.1016/j.jmaa.2005.08.090
Xu FY: Positive solutions for third-order nonlinear -Laplacian -point boundary value problems on time scales. Discrete Dynamics in Nature and Society 2008, 2008:-16.
Su YH, Li S, Huang C: Positive solution to a singular -Laplacian BVPs with sign-changing nonlinearity involving derivative on time scales. Advances in Difference Equations 2009, 2009:-21.
Su YH, Li WT: Existence of positive solutions to a singular -Laplacian dynamic equations with sign changing nonlinearity. Acta Mathematica Scientia 2009, 52: 181–196.
Xu FY: Positive solutions for multipoint boundary value problems with one-dimensional -Laplacian operator. Applied Mathematics and Computation 2007,194(2):366–380. 10.1016/j.amc.2007.04.118
Su YH, Li WT: Existence of positive solutions to a singular -Laplacian dynamic equations with sign changing nonlinearity. Acta Mathematica Scientia 2008, 28: 51–60.
Su Y-H: Multiple positive pseudo-symmetric solutions of -Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2009,49(7–8):1664–1681. 10.1016/j.mcm.2008.10.010
Su Y-H, Li W-T, Sun H-R: Positive solutions of singular -Laplacian BVPs with sign changing nonlinearity on time scales. Mathematical and Computer Modelling 2008,48(5–6):845–858. 10.1016/j.mcm.2007.11.008
Zhou C, Ma D: Existence and iteration of positive solutions for a generalized right-focal boundary value problem with -Laplacian operator. Journal of Mathematical Analysis and Applications 2006,324(1):409–424. 10.1016/j.jmaa.2005.10.086
Anderson DR: Green's function for a third-order generalized right focal problem. Journal of Mathematical Analysis and Applications 2003,288(1):1–14. 10.1016/S0022-247X(03)00132-X
Lan KQ: Multiple positive solutions of semilinear differential equations with singularities. Journal of the London Mathematical Society 2001,63(3):690–704. 10.1112/S002461070100206X
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgment
This project was supported by the National Natural Science Foundation of China (10471075, 10771117).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, F., Meng, Z. The Existence of Positive Solutions for Third-Order  -Laplacian
-Laplacian 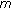 -Point Boundary Value Problems with Sign Changing Nonlinearity on Time Scales.
Adv Differ Equ 2009, 169321 (2009). https://doi.org/10.1155/2009/169321
-Point Boundary Value Problems with Sign Changing Nonlinearity on Time Scales.
Adv Differ Equ 2009, 169321 (2009). https://doi.org/10.1155/2009/169321
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/169321