- Research Article
- Open access
- Published:
Infinite Horizon Discrete Time Control Problems for Bounded Processes
Advances in Difference Equations volume 2008, Article number: 654267 (2009)
Abstract
We establish Pontryagin Maximum Principles in the strong form for infinite horizon optimal control problems for bounded processes, for systems governed by difference equations. Results due to Ioffe and Tihomirov are among the tools used to prove our theorems. We write necessary conditions with weakened hypotheses of concavity and without invertibility, and we provide new results on the adjoint variable. We show links between bounded problems and nonbounded ones. We also give sufficient conditions of optimality.
1. Introduction
The first works on infinite horizon optimal control problems are due to Pontryagin and his school [1]. They were followed by few others [2–6]. We consider in this paper an infinite horizon Optimal Control problem in the discrete time framework. Such problems are fundamental in the macroeconomics growth theory [7–10] and see references of [11]. Even in the finite horizon case, the discrete time framework presents significant differences from the continuous time one. Boltianski [12] shows that in the discrete time case, a convexity condition is needed to guarantee a strong Pontryagin Principle while this last one can be obtained without such condition in the continuous time setting. We study our problem in the space of bounded sequences  which allows us to use Analysis in Banach spaces instead of using reductions to finite horizon problems as in [5, 6]. According to Chichlinisky [13, 14], the space of bounded sequences was first used in economics by Debreu [15]. It can also be found in [7, 8, 16]. We obtain Pontryagin Maximum Principles in the strong form using weaker convexity hypotheses than the traditional ones and without invertibility [5]. When we study the problem in a general sequence space it turns out that the infinite series will not always converge. Therefore we present other notions of optimality that are currently used, notably in the economic literature, see [3, 4, 9] and we show how our problem can be related to these other problems. We end the paper by establishing sufficient conditions of optimality.
which allows us to use Analysis in Banach spaces instead of using reductions to finite horizon problems as in [5, 6]. According to Chichlinisky [13, 14], the space of bounded sequences was first used in economics by Debreu [15]. It can also be found in [7, 8, 16]. We obtain Pontryagin Maximum Principles in the strong form using weaker convexity hypotheses than the traditional ones and without invertibility [5]. When we study the problem in a general sequence space it turns out that the infinite series will not always converge. Therefore we present other notions of optimality that are currently used, notably in the economic literature, see [3, 4, 9] and we show how our problem can be related to these other problems. We end the paper by establishing sufficient conditions of optimality.
Now we briefly describe the contents of the paper. In Section 2 we introduce the notations and the problem, then we state Theorems 2.1 and 2.2 which give necessary conditions of optimality namely the existence of the adjoint variable in the space  satisfying the adjoint equation and the strong Pontryagin maximum principle. In Section 3 we prove these theorems through some lemmas and using results due to Ioffe-Tihomirov [17]. In Section 4 we introduce some other notions of optimality for problems in the nonbounded case and we show links with our problem. For example, we show that when the objective function is positive then a bounded solution is a solution among the unbounded processes. Finally we give sufficient conditions of optimality for problems in the bounded and unbounded cases adapting for each case the approprate transversality condition.
satisfying the adjoint equation and the strong Pontryagin maximum principle. In Section 3 we prove these theorems through some lemmas and using results due to Ioffe-Tihomirov [17]. In Section 4 we introduce some other notions of optimality for problems in the nonbounded case and we show links with our problem. For example, we show that when the objective function is positive then a bounded solution is a solution among the unbounded processes. Finally we give sufficient conditions of optimality for problems in the bounded and unbounded cases adapting for each case the approprate transversality condition.
2. Pontryagin maximum principles for bounded processes
We first precise our notations. Let  be a nonempty open convex subset of
be a nonempty open convex subset of  and
and  a nonempty compact subset of
a nonempty compact subset of  Let
Let  and, for all
and, for all  We set
We set 
Define 
For every  define
define  as the closure of the set of terms of the sequence
as the closure of the set of terms of the sequence  If
If 
 is compact. We set
is compact. We set  such that
such that  is thus the set of the bounded sequences which are in the interior of
is thus the set of the bounded sequences which are in the interior of  Note that
Note that  is a convex open subset of
is a convex open subset of  since
since  is open and convex. We set
is open and convex. We set  Define
Define  ; it is the set of admissible processes with respect to the considered dynamical system.
; it is the set of admissible processes with respect to the considered dynamical system.
Let  We consider first the following problem (P1):
We consider first the following problem (P1):

which can be written as follows.
(P1) Maximize  when
when 
Theorem 2.1.
Let  be a solution of (P1). Assume the following.
be a solution of (P1). Assume the following.
-
(i)
For all
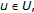 the mapping
the mapping  is of class
is of class  on
on  and for all
and for all  the mapping
the mapping 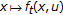 is Fréchet-differentiable on
is Fréchet-differentiable on 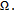
-
(ii)
For all
 for all
for all  for all
for all  for all
for all 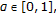 there exists
there exists  such that
such that 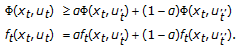 (2.1)
(2.1)
-
(iii)
For any compact set
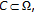 there exists a constant
there exists a constant 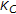 such that for all
such that for all  for all
for all  for all
for all  and
and 
-
(iv)
There exists
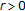 such that
such that 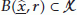 and for all
and for all 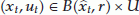
 (2.2)
(2.2)
Then there exists  such that
such that
-
(a)

-
(b)
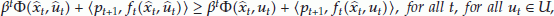
-
(c)
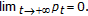
Comments
For continuous time problems, one does not need conditions to obtain a strong Pontryagin maximum principle, both in the finite horizon case (see, e.g., [18]) and in the infinite horizon case (see, e.g., [5]). But for discrete time problems, strong Pontryagin principles cannot hold without an additional assumption namely a convexity condition, as Boltyanski shows in [12] for the finite horizon framework. Condition (ii) comes from the Ioffe and Tihomirov book [17]. It generalizes the usual convexity condition used to garantee a strong Pontryagin maximum principle. The usual condition is:  convex subset,
convex subset,  concave with respect to
concave with respect to  and for every
and for every 
 affine with respect to
affine with respect to  It implies condition (ii). In (iii) the condition
It implies condition (ii). In (iii) the condition  is satisfied when
is satisfied when  is continuous (since
is continuous (since  is compact) and the condition
is compact) and the condition  is satisfied when
is satisfied when  exists and is continuous.
exists and is continuous.
Conclusion (a) is the adjoint equation, conclusion (b) is the strong Pontryagin maximum principle and conclusion (c) is a transversality condition at infinity. In our case (c) is immediately obtained since  is in
is in  but in general (nonbounded cases) it is very delicate to obtain such a conclusion. [9]
but in general (nonbounded cases) it is very delicate to obtain such a conclusion. [9]
In the next theorem we consider the autonomous case. Thus the hypotheses are simpler and easier to manipulate.
Theorem 2.2.
Let  for all
for all  Let
Let  be a solution of (P1). Assume that the following conditions are fulfilled.
be a solution of (P1). Assume that the following conditions are fulfilled.
-
(i)
For all
 the mappings
the mappings  and
and  are of class
are of class 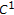 on
on 
-
(ii)
For all
 for all
for all  for all
for all 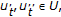 for all
for all  there exists
there exists  such that
such that  (2.3)
(2.3)
-
(iii)
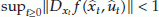
Then there exists  such that the assertions (a), (b), and (c) of Theorem 2.1 are satisfied.
such that the assertions (a), (b), and (c) of Theorem 2.1 are satisfied.
3. Proofs of Theorems 2.1 and 2.2
Proof of Theorem 2.1
First Part
The first part of the proof goes through several lemmas.
Lemma 3.1.
 is well-defined and under hypothesis (i) of Theorem 2.1, for all
is well-defined and under hypothesis (i) of Theorem 2.1, for all  the mapping
the mapping  is of class
is of class  and one has, for all
and one has, for all 

For the proof see [19].
We set  for all
for all 
Lemma 3.2.
Assume that hypothesis (iii) of Theorem 2.1 holds. Then for  one has
one has  Moreover, if in addition hypotheses (i) and (iv) of Theorem 2.1 hold, then for all
Moreover, if in addition hypotheses (i) and (iv) of Theorem 2.1 hold, then for all  the mapping
the mapping  is of class
is of class  on the ball
on the ball  in
in  and for all
and for all  one has
one has 
Proof.
Let  Let
Let  be the constant of (iii) with
be the constant of (iii) with  So for all
So for all  So one has
So one has 
Assume now that hypotheses (i) and (iv) of Theorem 2.1 hold. Let us show that  is of class
is of class  on
on  Take
Take  Let
Let  be given. Let
be given. Let  be such that
be such that  Then, for all
Then, for all 





 under (iv), which implies that
under (iv), which implies that 
Let us now show that  is Fréchet-differentiable on
is Fréchet-differentiable on  Take
Take  Let
Let  be given. Let
be given. Let  be such that
be such that  Then, for all
Then, for all 




 under (iii). But this implies that
under (iii). But this implies that 

 Thus
Thus  is Fréchet-differentiable at
is Fréchet-differentiable at  and
and 


To show the continuity of  at
at  let
let  be the constant of hypothesis (iii) corresponding to
be the constant of hypothesis (iii) corresponding to  Let
Let  be given and let
be given and let  be such that
be such that 



 So
So  is of class
is of class 
Lemma 3.3.
Under hypothesis (ii) of Theorem 2.1, for all  for all
for all  for all
for all  there exists
there exists  such that
such that

Proof.
Let  and
and  Hypothesis (ii) of Theorem 2.1 implies for all
Hypothesis (ii) of Theorem 2.1 implies for all  the existence of
the existence of  such that
such that

Therefore we obtain

Set  so
so  and satisfies the required relations.
and satisfies the required relations.
Lemma 3.4.
Under hypotheses (i) and (iv) of Theorem 2.1, 
Proof.
Since 
 the problem is a problem of bounded solutions of first-order linear difference equations.
the problem is a problem of bounded solutions of first-order linear difference equations.
Let  Assume that
Assume that  Then for all
Then for all  there exists a unique
there exists a unique  such that for all
such that for all 

where 
Consider the operator  such that for all
such that for all 

 where
where

Recall that the  norm of
norm of  is defined by
is defined by  and that the norm of a linear operator
and that the norm of a linear operator  between normed spaces is defined by
between normed spaces is defined by 
So  So
So  Since
Since  and
and 
 is invertible so it is surjective.
is invertible so it is surjective.
Set  Then under (iv) one has
Then under (iv) one has  So
So  is surjective that is
is surjective that is 
Recall that  where
where  consists of all singular functionals, see Aliprantis and Border [20]. In fact it consists (up to scalar multiples) of all extensions of the "limit functional" to
consists of all singular functionals, see Aliprantis and Border [20]. In fact it consists (up to scalar multiples) of all extensions of the "limit functional" to 
If  then there exists
then there exists  such that for all
such that for all  (
( being the space of convergent sequences having a limit in
being the space of convergent sequences having a limit in  )
)
Lemma 3.5 ( ).
).
If  then
then  where
where  for every
for every  So there exists
So there exists  such that for all
such that for all 
Second Part
Our optimal control problem can be written as the following abstract static optimisation problem in a Banach space:

that satisfies all conditions of Theorem 4.3, Ioffe-Tihomirov [17]. So we can apply this theorem and obtain the existence of  not all zero,
not all zero,  such that:
such that:

(AE) denotes the adjoint equation of this problem and (PMP) the Pontryagin maximum principle. They can be written, respectively:

Set  where
where  and
and 
(AE) becomes:

So we get

Let  be arbitrarily chosen in
be arbitrarily chosen in  and let
and let  be in
be in  Consider the sequence
Consider the sequence  defined as follows:
defined as follows:

So one has  if
if  hence
hence 
Thus, it holds that 
Now 
Therefore, for all  and for all
and for all  one has
one has

which implies

that is,

(PMP) becomes:

So  for all
for all 
Consider, for all  the sequences
the sequences  defined as follows:
defined as follows:

Since the inequality holds for every  we obtain
we obtain

using  as
as  is of finite support.
is of finite support.
Lemma 3.6.
( ).
).
Proof.
Recall we obtained the existence of  not all zero,
not all zero,  such that:
such that:

If  then
then  since
since 
Hence  We can set it equal to one.
We can set it equal to one.
From Lemma 3.6 and the previous results, conclusions (a) and (b) are satisfied.
Conclusion (c) is a straightforward consequence of the belonging of  to
to 
Lemma 3.7.
( ).
).
Proof.
Indeed we obtained  for all
for all  Using
Using  one has
one has  for all
for all  Thus
Thus 
Proof of Theorem 2.2.
Define  on
on  such that
such that  Under hypothesis (i) of Theorem 2.2, for all
Under hypothesis (i) of Theorem 2.2, for all  the mappings
the mappings  and
and  are of class
are of class  on
on  The proof can be found in [19].
The proof can be found in [19].
We consider the proof of Lemma 3.4 and we set  Then the proof goes like that of Theorem 2.1.
Then the proof goes like that of Theorem 2.1.
4. Results for unbounded problems
We study now problems of maximization over admissible processes which are not necessarily bounded when the optimal solution is bounded. So consider the following problems.
(P2) Maximize  on
on 
(P3) Find  such that, for all
such that, for all 

(P4) Find  such that, for all
such that, for all 

(P5) Find  such that, for all
such that, for all 

The optimality notion of (P3) is called "the strong optimality," that of (P4) is called "the overtaking optimality" and that of (P5) the "weak overtaking optimality" in [3] (in the continuous-time framework). Many existence results of overtaking optimal solutions and weakly overtaking optimal solutions are obtained in [3, 4]. In [4] there are also results in the discrete-time framework.
Remark 4.1.
Notice that  is an optimal solution of (P3) implies
is an optimal solution of (P3) implies  is an optimal solution of (P4) which implies
is an optimal solution of (P4) which implies  is an optimal solution of (P5).
is an optimal solution of (P5).
Moreover if  is a bounded optimal solution of (P4) then (P3) and (P4) reduce to the same problem.
is a bounded optimal solution of (P4) then (P3) and (P4) reduce to the same problem.
Lemma 4.2.
The two following assertions hold.
-
(a)
If
 is an optimal solution of problem (P2), (P3), (P4) or (P5) and
is an optimal solution of problem (P2), (P3), (P4) or (P5) and  then
then 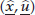 is an optimal solution of problem (P1). Therefore Theorem 2.1 applies.
is an optimal solution of problem (P1). Therefore Theorem 2.1 applies. -
(b)
Assume
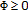 on
on  If
If 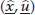 is an optimal solution of problem (P3) or (P4) and
is an optimal solution of problem (P3) or (P4) and  then
then 
Proof. (a) Since  a bounded optimal solution of (P2) or (P3) is an optimal solution of (P1). Suppose now that
a bounded optimal solution of (P2) or (P3) is an optimal solution of (P1). Suppose now that  is a bounded optimal solution of (P4) that is
is a bounded optimal solution of (P4) that is  for all
for all  Since
Since  this can be written
this can be written  for all
for all  and so in particular for all
and so in particular for all 
In that case  The proof is analogous for (P5).
The proof is analogous for (P5).
(b) If  is an optimal solution of problem (P3) and
is an optimal solution of problem (P3) and  one has
one has  for all
for all  Since
Since  the sequence
the sequence  is increasing and since it is also upper bounded it converges in
is increasing and since it is also upper bounded it converges in 
So  and
and 
Theorem 4.3.
Let  for all
for all  One assumes the following conditions fulfilled:
One assumes the following conditions fulfilled:
-
(i)
 on
on 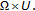
-
(ii)
For all
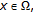 there exists
there exists 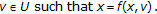
Then one has
-
(a)

-
(b)
If
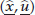 is an optimal solution of problem (P1), then it is an optimal solution of problems (P3), (P4), and (P5) which all reduce to the same problem.
is an optimal solution of problem (P1), then it is an optimal solution of problems (P3), (P4), and (P5) which all reduce to the same problem.
Remark 4.4. (b) shows that under a nonnegativity assumption, solving the problem in the space of bounded processes provides solutions for problems in spaces of admissible processes which are not necessarily bounded. This type of results is in the spirit of Blot and Cartigny [21] where problems are studied in the continuous-time case.
Proof. (a) It is clear that the following inequality holds:

Let  Let
Let  be given and let
be given and let  be such that
be such that  Set
Set

where  is such that
is such that 
 and
and  are bounded and
are bounded and 
Since  on
on  one has
one has

so we obtain

Since this is true fo all  letting
letting  we obtain
we obtain

(b) Since  for all
for all  the sequence
the sequence  is nonnegative and nondecreasing so it converges in
is nonnegative and nondecreasing so it converges in 
So  Hence (P3), (P4) reduce to the same problem. Similarly (P5) reduces to it. Let
Hence (P3), (P4) reduce to the same problem. Similarly (P5) reduces to it. Let  be an optimal solution of problem (P1) and suppose it is not an optimal solution of problem (P3). So there exists
be an optimal solution of problem (P1) and suppose it is not an optimal solution of problem (P3). So there exists  such that
such that  that is
that is

Let  and
and  Construct
Construct  and
and  as in (a). Thus
as in (a). Thus 
Hence we obtain  so
so  which contradicts the hypothesis so
which contradicts the hypothesis so  is an optimal solution of problem (P3).
is an optimal solution of problem (P3).
Following Michel, [22], for all  and for all
and for all  we define
we define  as the set of the
as the set of the  for which there exists
for which there exists  satisfying
satisfying 
 We also define
We also define  as the set of the
as the set of the  for which there exists
for which there exists  satisfying
satisfying 
 for all
for all 
Theorem 4.5.
Let  for all
for all  Let
Let  be an optimal solution of problem (P1). One assumes the following conditions fulfilled.
be an optimal solution of problem (P1). One assumes the following conditions fulfilled.
-
(i)
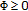 on
on 
-
(ii)
For all
 there exists
there exists 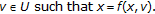
-
(iii)
For all
 the mappings
the mappings  and
and 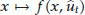 are Fréchet-differentiable at
are Fréchet-differentiable at 
-
(iv)
For all
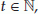 for all
for all  co
co where co denotes the convex hull.
where co denotes the convex hull. -
(v)
For all

 is invertible.
is invertible.
Then there exists  such that
such that  and
and
-
(a)

-
(b)
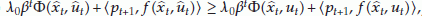 for all
for all  for all
for all 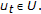
Remark 4.6.
Notice that condition (iv) is a convexity condition and that condition (ii) of Theorem 2.2 implies this condition (iv). Condition (ii) of Theorem 2.2 is equivalent to the following condition: for all  the set
the set  is convex.
is convex.
Proof.
Use Theorem 4.3 of this paper and apply Theorem 3 in Blot-Chebbi [5].
5. Sufficient conditions of optimality
Let  for all
for all 
Theorem 5.1.
Let  where
where  is convex. One assumes that there exists
is convex. One assumes that there exists  and that the following conditions are fulfilled.
and that the following conditions are fulfilled.
-
(i)
The mappings
 and for all
and for all 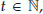
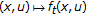 are of class
are of class 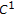 on
on 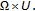
-
(ii)

-
(iii)
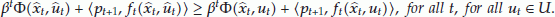
-
(iv)
The mapping
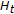 is concave with respect to
is concave with respect to 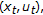 for all
for all 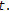
Then  is an optimal solution of (P1).
is an optimal solution of (P1).
Proof.
Notice that from (ii),  for all
for all 
Let  For all
For all  one has
one has

therefore, we obtain

Since for all 
 is concave with respect to
is concave with respect to  and
and  one has
one has  Using hypothesis (iii) with
Using hypothesis (iii) with  gives
gives  and using hypothesis (iii), the first order necessary condition for the optimality of
and using hypothesis (iii), the first order necessary condition for the optimality of  is
is  Thus one has
Thus one has 
The hypothesis  implies
implies  and since
and since  and
and  belong to
belong to  one has
one has  Hence we obtain
Hence we obtain  so
so  That is
That is 
Corollary 5.2.
Let  (resp.,
(resp.,  ). If the hypotheses of the previous theorem are satisfied except that
). If the hypotheses of the previous theorem are satisfied except that  is replaced by
is replaced by  and if the following hypothesis is also satisfied:
and if the following hypothesis is also satisfied:
-
(v)

then  is a solution of (P3) (resp., (P4)).
is a solution of (P3) (resp., (P4)).
Notice that if  with
with  we obtain that
we obtain that  is a solution of (P5).
is a solution of (P5).
One can weaken the hypothesis of concavity of  with respect to
with respect to  and
and  and replace it by the concavity of
and replace it by the concavity of  with respect to
with respect to  as the following theorem shows. (See [23] for a quick survey of sufficient conditions.)
as the following theorem shows. (See [23] for a quick survey of sufficient conditions.)
Let 
The maximum is attained since  is compact.
is compact.
Theorem 5.3.
Let  One assumes that there exists
One assumes that there exists  and that the following hypotheses are fulfilled.
and that the following hypotheses are fulfilled.
-
(i)
For all
 the mappings
the mappings  and for all
and for all 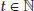
 are of class
are of class 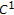 on
on 
-
(ii)
Also (iii) of the previous theorem.
-
(iv)
The mapping
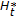 is concave with respect to
is concave with respect to 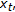 for all
for all 
Then  is an optimal solution of (P1).
is an optimal solution of (P1).
Proof.
Let  and let
and let  For all
For all  one has
one has

by the definition of  and noticing that
and noticing that  So we obtain
So we obtain

(Notice that  Now using
Now using  (see Seierstad and Sydsaeter [24, page 390]) we obtain
(see Seierstad and Sydsaeter [24, page 390]) we obtain 



 The concavity of
The concavity of  with respect to
with respect to  gives
gives  Finally
Finally  follows as in the proof of the previous theorem.
follows as in the proof of the previous theorem.
Corollary 5.4.
Let  (resp.,
(resp.,  ). If the hypotheses of the previous theorem are satisfied except that
). If the hypotheses of the previous theorem are satisfied except that  is replaced by
is replaced by  and if the following hypothesis is also satisfied:
and if the following hypothesis is also satisfied:
-
(v)

then  is a solution of (P3) (resp., (P4)).
is a solution of (P3) (resp., (P4)).
Notice that if  with
with  we obtain that
we obtain that  is a solution of (P5).
is a solution of (P5).
References
Pontryagin L, Boltianski V, Gramkrelidze R, Mitchenko E: Théorie Mathématique des Processus Optimaux. Mir, Moscow, Russia; 1974.
Ekeland I, Scheinkman JA: Transversality conditions for some infinite horizon discrete time optimization problems. Mathematics of Operations Research 1986, 11(2):216-229. 10.1287/moor.11.2.216
Carlson DA, Haurie AB, Leizarowitz A: Infinite Horizon Optimal Control. Deterministic and Stochastic Systems. 2nd edition. Springer, Berlin, Germany; 1991.
Zaslavski AJ: Turnpike Properties in the Calculus of Variations and Optimal Control, Nonconvex Optimization and Its Applications. Volume 80. Springer, New York, NY, USA; 2006:xxii+395.
Blot J, Chebbi H: Discrete time Pontryagin principles with infinite horizon. Journal of Mathematical Analysis and Applications 2000, 246(1):265-279. 10.1006/jmaa.2000.6797
Blot J, Hayek N: Infinite-horizon Pontryagin principles with constraints. In Communications of the Laufen Colloquium on Science, Laufen, Austria, Berichte aus der Mathematik, 2. Edited by: Ruffing A, Suhrer A, Suhrer J. Shaker, Aachen, Germany; 2007:1-14.
Araujo A, Scheinkman JA: Smoothness, comparative dynamics, and the turnpike property. Econometrica 1977, 45(3):601-620. 10.2307/1911677
Araujo A, Scheinkman JA: Notes on comparative dynamics. In General Equilibrium, Growth, and Trade. Edited by: Green JR, Scheinkman JA. Academic Press, New York, NY, USA; 1979:217-226.
Michel P: Some clarifications on the transversality condition. Econometrica 1990, 58(3):705-723. 10.2307/2938197
Stokey NL, Lucas RE Jr., Prescott EC: Recursive Methods in Economic Dynamics. Harvard University Press, Cambridge, Mass, USA; 1989:xviii+588.
Grinold R: Convex infinite horizon programs. Mathematical Programming 1983, 25(1):64-82. 10.1007/BF02591719
Boltianski V: Commande Optimale des Systèmes Discrets. Traduit du Russe par A. Sossinsk. Mir, Moscow, Russia; 1976:467.
Chichilnisky G: An axiomatic approach to sustainable development. Social Choice and Welfare 1996, 13(2):231-257. 10.1007/BF00183353
Chichlinisky G: What is sustainable development? Land Economics 1997, 73(4):46791.
Debreu G: Valuation equilibrium and Pareto optimum. Proceedings of the National Academy of Sciences of the United States of America 1954, 40(7):588-592. 10.1073/pnas.40.7.588
Peleg B, Ryder H: On optimal consumption plans in a multi-sector economy. Review of Economics Studies 1972, 39(2):159-169. 10.2307/2296868
Ioffe AD, Tihomirov VM: Theory of Extremal Problems, Studies in Mathematics and Its Applications. Volume 6. North-Holland, Amsterdam, The Netherlands; 1979:xii+460.
Alexéev V, Tikhomirov V, Fomine S: Commande Optimale. Mir, Moscow, Russia; 1982:447.
Blot J, Crettez B: On the smoothness of optimal paths. Decisions in Economics and Finance 2004, 27(1):1-34. 10.1007/s10203-004-0042-5
Aliprantis CD, Border KC: Infinite-Dimensional Analysis. 2nd edition. Springer, Berlin, Germany; 1999:xx+672.
Blot J, Cartigny P: Optimality in infinite-horizon variational problems under sign conditions. Journal of Optimization Theory and Applications 2000, 106(2):411-419. 10.1023/A:1004611816252
Michel P: Programmes mathématiques mixtes. Application au principe du maximum en temps discret dans le cas déterministe et dans le cas stochastique. RAIRO Recherche Opérationnelle 1980, 14(1):1-19.
Blot J, Hayek N: Sufficient conditions for infinite-horizon calculus of variations problems. ESAIM: Control, Optimisation and Calculus of Variations 2000, 5: 279-292.
Seierstad A, Sydsaeter K: Sufficient conditions in optimal control theory. International Economic Review 1977, 18(2):367-391. 10.2307/2525753
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Blot, J., Hayek, N. Infinite Horizon Discrete Time Control Problems for Bounded Processes. Adv Differ Equ 2008, 654267 (2009). https://doi.org/10.1155/2008/654267
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/654267
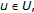 the mapping
the mapping  is of class
is of class  on
on  and for all
and for all  the mapping
the mapping 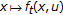 is Fréchet-differentiable on
is Fréchet-differentiable on 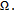
 for all
for all  for all
for all  for all
for all 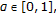 there exists
there exists  such that
such that 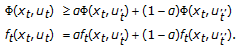
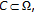 there exists a constant
there exists a constant 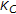 such that for all
such that for all  for all
for all  for all
for all  and
and 
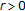 such that
such that 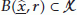 and for all
and for all 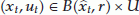


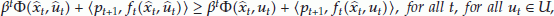
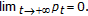
 the mappings
the mappings  and
and  are of class
are of class 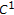 on
on 
 for all
for all  for all
for all 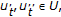 for all
for all  there exists
there exists  such that
such that 
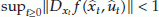
 is an optimal solution of problem (P2), (P3), (P4) or (P5) and
is an optimal solution of problem (P2), (P3), (P4) or (P5) and  then
then 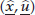 is an optimal solution of problem (P1). Therefore Theorem 2.1 applies.
is an optimal solution of problem (P1). Therefore Theorem 2.1 applies.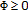 on
on  If
If 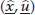 is an optimal solution of problem (P3) or (P4) and
is an optimal solution of problem (P3) or (P4) and  then
then 
 on
on 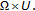
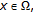 there exists
there exists 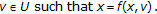

 is an optimal solution of problem (P1), then it is an optimal solution of problems (P3), (P4), and (P5) which all reduce to the same problem.
is an optimal solution of problem (P1), then it is an optimal solution of problems (P3), (P4), and (P5) which all reduce to the same problem. on
on 
 there exists
there exists 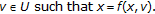
 the mappings
the mappings  and
and 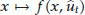 are Fréchet-differentiable at
are Fréchet-differentiable at 
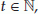 for all
for all  co
co where co denotes the convex hull.
where co denotes the convex hull.
 is invertible.
is invertible.
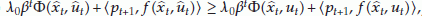 for all
for all  for all
for all 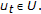
 and for all
and for all 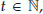
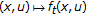 are of class
are of class 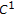 on
on 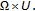

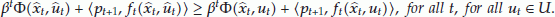
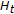 is concave with respect to
is concave with respect to 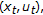 for all
for all 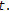

 the mappings
the mappings  and for all
and for all 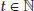
 are of class
are of class 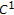 on
on 
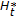 is concave with respect to
is concave with respect to 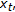 for all
for all 
