- Research Article
- Open access
- Published:
Absolute Stability of Discrete-Time Systems with Delay
Advances in Difference Equations volume 2008, Article number: 396504 (2007)
Abstract
We investigate the stability of nonlinear nonautonomous discrete-time systems with delaying arguments, whose linear part has slowly varying coefficients, and the nonlinear part has linear majorants. Based on the "freezing" technique to discrete-time systems, we derive explicit conditions for the absolute stability of the zero solution of such systems.
1. Introduction
Over the past few decades, discrete-time systems with delay have drawn much attention from the researchers. This is due to their important role in many practical systems. The stability of time-delay systems is a fundamental problem because of its importance in the analysis of such systems.The basic method for stability analysis is the direct Lyapunov method, for example, see [1–3], and by this method, strong results have been obtained. But finding Lyapunov functions for nonautonomous delay difference systems is usually a difficult task. In contrast, many methods different from Lyapunov functions have been successfully applied to establish stability results for difference equations with delay, for example, see [3–12].
This paper deals with the absolute stability of nonlinear nonautonomous discrete-time systems with delay, whose linear part has slowly varying coefficients, and the nonlinear part satisfies a Lipschitz condition.
The aim of this paper is to generalize the approach developed in [7] for linear nonautonomous delay difference systems to the nonlinear case with delaying arguments. Our approach is based on the "freezing" technique for discrete-time systems. This method has been used to investigate properties as well as to the construction of solutions for systems of linear differential equations. So, it is commonly used in analysing the stability of slowly varying initial-value problems as well as solving them, for example, see [13, 14]. However, its use to difference equations is rather new [7]. The stability conditions will be formulated assuming that we know the Cauchy solution (fundamental solution) of the unperturbed system.
The paper is organized as follows. After some preliminaries in Section 2, the sufficient conditions for the absolute stability are presented in Section 3. In Section 4, we reduce a delay difference system to a delay-free linear system of higher dimension, thus obtaining explicit stability conditions for the solutions.
2. Preliminaries
Let  denote the set of nonnegative integers. Given a positive integer
denote the set of nonnegative integers. Given a positive integer  , denote by
, denote by  and
and  the
the  -dimensional space of complex column vectors and the set of
-dimensional space of complex column vectors and the set of  matrices with complex entries, respectively. If
matrices with complex entries, respectively. If  is any norm on
is any norm on  , the associated induced norm of a matrix
, the associated induced norm of a matrix  is defined by
is defined by

Consider the nonlinear discrete-time system with multiple delays of the form

where  is an integer
is an integer  and
and 
We will consider (2.2) subject to the initial conditions

where  is a given vector-valued function, that is,
is a given vector-valued function, that is, 
Throughout the paper, we will assume that the variable matrices  have the properties
have the properties


In addition, 



 is a given function satisfying the growth condition
is a given function satisfying the growth condition

where  ;
;  ;
;  ,
, 
Definition 2.1.
The zero solution of (2.2) is absolutely stable in the class of nonlinearities (2.6) if there is a positive constant  , independent of
, independent of  (but dependent on
(but dependent on  ), such that
), such that

for any solution  of (2.2) with the initial conditions (2.3).
of (2.2) with the initial conditions (2.3).
It is clear that every solution  of the initial-valued problem (2.2)-(2.3) exists, is unique and can be constructed recursively from (2.2).
of the initial-valued problem (2.2)-(2.3) exists, is unique and can be constructed recursively from (2.2).
Put

The stability conditions for (2.2) will be formulated in terms of the Cauchy function  (the fundamental solution) of
(the fundamental solution) of

defined as follows. For a fixed  let
let  be the solution of (2.9) with initial conditions
be the solution of (2.9) with initial conditions

Since the coefficients of (2.9) are constants for fixed  , then the Cauchy function of (2.9) has the form
, then the Cauchy function of (2.9) has the form

where  is the solution of (2.9) with the initial conditions
is the solution of (2.9) with the initial conditions

In order to state and prove our main results, we need some suitable lemmas and theorems.
Lemma 2.2 (see [7]).
The solution  of
of

where 
 is a given function, subject to the initial conditions
is a given function, subject to the initial conditions

has the form

where  is the Cauchy function of (2.9) and
is the Cauchy function of (2.9) and  is the solution of the homogeneous equation
is the solution of the homogeneous equation

with the same initial conditions:

Lemma 2.3 (see [7]).
The solution  of (2.16) with initial conditions (2.14) has the form
of (2.16) with initial conditions (2.14) has the form

In [7], was established the following stability result in terms of the Cauchy solution  of (2.9).
of (2.9).
Theorem 2.4 (see [7]).
Let the inequality

holds with constant  , and
, and  independent of
independent of  . If in addition, conditions (2.4), (2.5), and
. If in addition, conditions (2.4), (2.5), and  are fulfilled, then (2.16) is stable.
are fulfilled, then (2.16) is stable.
Our purpose is to generalize this result to the nonlinear problem (2.2)-(2.3).
Lemma 2.5 (see [9]).
Let  be a sequence of positive numbers such that
be a sequence of positive numbers such that

where  is a constant. Then there exist constants
is a constant. Then there exist constants  and
and  such that
such that

3. Main Results
Now, we establish the main results of the paper, which will be valid for a family 
 of slowly varying matrices. Let
of slowly varying matrices. Let  and
and  With the notation
With the notation

assume that

Consider the equation

where 
 is a bounded function such that
is a bounded function such that

Theorem 3.1.
Under conditions (2.4) and (2.5), let the inequality

holds. Then for any solution  of problem (2.13)–(2.3), the estimate
of problem (2.13)–(2.3), the estimate

is valid, where  , and
, and 
Proof.
Fix  and rewrite (3.3) in the form
and rewrite (3.3) in the form

Making

we get

A solution of the latter equation, subject to the initial conditions (2.3), can be represented as

where  is the solution of the homogeneous equation (2.9) with initial conditions (2.3). Since
is the solution of the homogeneous equation (2.9) with initial conditions (2.3). Since  is a solution of (2.9), we can write
is a solution of (2.9), we can write

This relation and (2.5) yield

since the Cauchy function is bounded by (3.2). Moreover,

From (3.10), it follows that

According to (2.4), we have

Take  . Then, by the estimate
. Then, by the estimate

it follows that

Hence,

where

Making

we obtain

Condition (3.5) implies the inequality

Since  is arbitrary, we obtain the estimate
is arbitrary, we obtain the estimate

Further,

This yields the required result.
Corollary 3.2.
Under conditions (2.4) and (2.5), let the inequality

hold, with constants  and
and  independent of
independent of  . If, in addition,
. If, in addition,

Then, any solution  of (2.13)–(2.3) satisfies the estimate
of (2.13)–(2.3) satisfies the estimate

where  , and
, and 
Proof.
Under condition (3.25), we obtain

Now, Corollary 3.2 yields the following result.
Theorem 3.3.
Let the conditions (2.4), (2.5), (2.6), (3.25), and, in addition,

hold. Then, the zero solution of (2.2)-(2.3) is absolutely stable in the class of nonlinearities in (2.6).
Proof.
Condition (3.29) implies the inequality (3.26), and in addition

By (2.6), we obtain

where  is a solution of (2.2) and
is a solution of (2.2) and 
Let

then (2.2) takes the form (3.3). Thus, Corollary 3.2 implies

Thus, condition (3.29) implies

where

This fact proves the required result.
Remark 3.4.
Theorem 3.3 is exact in the sense that if (2.2) is a homogeneous linear stable equation with constant matrices  , then
, then  , and condition (3.29) is always fulfilled.
, and condition (3.29) is always fulfilled.
It is somewhat inconvenient that to apply either condition (3.26) or (3.29), one has to assume explicit knowledge of the constants  and
and  . In the next theorem, we will derive sufficient conditions for the exponential growth of the Cauchy function associated to (2.9). Thus, our conditions may provide a useful tool for applications.
. In the next theorem, we will derive sufficient conditions for the exponential growth of the Cauchy function associated to (2.9). Thus, our conditions may provide a useful tool for applications.
Theorem 3.5 (see [7]).
Assume that the Cauchy function  of (2.9) satisfies
of (2.9) satisfies

where  is a constant. Then there exist constants
is a constant. Then there exist constants  and
and  such that
such that

Now, we will consider the homogeneous equation (2.16), thus establishing the following consequence of Theorem 3.3.
Corollary 3.6.
Let conditions (2.4), (2.5), (3.25), and, in addition,

hold. Then the zero solution of (2.16)–(2.3) is absolutely stable.
Example 3.7.
Consider the following delay difference system in the Euclidean space  :
:

where

and  . And
. And  ,
,  , are positive bounded sequences withthe following properties:
, are positive bounded sequences withthe following properties:  and
and  and
and  ;
;  , are nonnegative constants for
, are nonnegative constants for  . This yields that
. This yields that  and
and  , respectively, for
, respectively, for  . Thus
. Thus  .
.
In addition, the function  supplies the solvability and satisfies the condition
supplies the solvability and satisfies the condition

Hence, 
Further, assume that the Cauchy solution  of equation
of equation

for a fixed  tends to zero exponentially as
tends to zero exponentially as  that is, there exist constants
that is, there exist constants  and
and  such that
such that  ;
; 
If  , then by Theorem 3.3, it follows that the zero solution of (3.39) is absolutely stable.
, then by Theorem 3.3, it follows that the zero solution of (3.39) is absolutely stable.
For instance, if the linear system with constant coefficients associated to the nonlinear system with variable coefficients (3.39) is

then it is not hard to check that the Cauchy solution of this system tends to zero exponentially as  Hence, by Theorem 3.3, it follows that the zero solution of (3.39) is absolutely stable provided that the relation (3.29) is satisfied.
Hence, by Theorem 3.3, it follows that the zero solution of (3.39) is absolutely stable provided that the relation (3.29) is satisfied.
4. Linear Delay Systems
Now, we will consider an important particular case of (2.2), namely, the linear delay difference system

where 
 and
and  are variable
are variable  -matrices.
-matrices.
In [4], were established very nice solution representation formulae to the system

assuming that  and
and  However, the stability problem was not investigated in this paper.
However, the stability problem was not investigated in this paper.
Kipnis and Komissarova [6] investigated the stability of the system

where  are
are  -matrices,
-matrices, 
 By means of a characteristic equation, they established many results concerning the stability of the solutions of such equation. However, the case of variable coefficients is not studied in this article.
By means of a characteristic equation, they established many results concerning the stability of the solutions of such equation. However, the case of variable coefficients is not studied in this article.
In the next corollary, we will apply Theorem 3.3 to this particular case of (2.2), thus obtaining the following corollary.
Corollary 4.1.
Under condition (3.25), one assumes that
(i)the matrices  and
and  satisfy
satisfy  and
and  , respectively, for
, respectively, for 
(ii)

-
(iii)
 (4.4)
(4.4)
Then, the zero solution of (4.1)-(2.3) is absolutely stable.
Remark 4.2.
I want to point out that this approach is just of interest for systems with "slowly changing" matrices.
The purpose of this section is to apply a new method to investigate the stability of system (4.1), which combined with the "freezing technique," will allow us to derive explicit estimations to their solutions, namely, introducing new variables; one can reduce system (4.1) to a delay-free linear difference system of higher dimension. In fact, put

Then (4.1) takes the form

where

where  is the unit matrix in
is the unit matrix in 
Let  be the product of
be the product of  copies of
copies of  Then we can consider (4.6) defined in the space
Then we can consider (4.6) defined in the space  . In
. In  define the norm
define the norm

For an  -matrix
-matrix  , denote
, denote

where  is the Frobenius (Hilbert-Schmidt) norm of a matrix
is the Frobenius (Hilbert-Schmidt) norm of a matrix  ,
, 
 , and
, and  are the eigenvalues of
are the eigenvalues of  , including their multiplicities. Here
, including their multiplicities. Here  is the adjoint matrix. If
is the adjoint matrix. If  is normal, that is,
is normal, that is,  , then
, then  If
If  is a triangular matrix such that
is a triangular matrix such that  for
for  , then
, then

Due to [15, Theorem 2.1], for any  -matrix
-matrix  , the inequality
, the inequality

holds for every nonnegative integer  , where
, where  is the spectral radius of
is the spectral radius of  .
.
Theorem 4.3 (see [7]).
Assume that
-
(i)
 ;
; 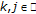 and
and 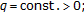
-
(ii)
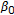 =
=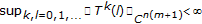 ,
, 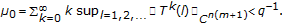
Then, any solution  of (4.1) is bounded and satisfies the inequality
of (4.1) is bounded and satisfies the inequality

where  , with
, with  defined in (2.14).
defined in (2.14).
Since the calculation of quantities  and
and  is not an easy task, by (4.11), some estimations to these formulae, namely, in terms of the eigenvalues of auxiliary matrices will be driven. In doing so, one assumes that
is not an easy task, by (4.11), some estimations to these formulae, namely, in terms of the eigenvalues of auxiliary matrices will be driven. In doing so, one assumes that

and denote

where  and
and  .
.
Corollary 4.4.
Under condition (i) of Theorem 4.3, let (4.13) and  hold. Then, any solution
hold. Then, any solution  of (4.1) is bounded. Moreover,
of (4.1) is bounded. Moreover,

where 
Proof.
By (4.11), we obtain

The relation

implies that

Simple calculations show that

Thus,

Hence,  .
.
On the other hand,

But

Thus, it follows that

Remark 4.5.
This approach is usually not applicable to the time-varying delay case, because the transformed systems usually have time-varying matrix coefficients, which are difficult to analyze using available tools. Hence, our results will provide new tools to analyze these kind of systems.
References
Agarwal RP: Difference Equations and Inequalities. Theory, Methods, and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 155. Marcel Dekker, New York, NY, USA; 1992:xiv+777.
Lakshmikantham V, Trigiante D: Theory of Difference Equations, Mathematics in Science and Engineering. Volume 181. Academic Press, Boston, Mass, USA; 1988:x+242.
Vidyasagar M: Nonlinear Syatems Analysis. Prentice-Hall, Englewood-Cliffs, NJ, USA; 1978.
Diblík J, Khusainov DYa:Representation of solutions of discrete delayed system
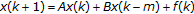 with commutative matrices. Journal of Mathematical Analysis and Applications 2006, 318(1):63-76. 10.1016/j.jmaa.2005.05.021
with commutative matrices. Journal of Mathematical Analysis and Applications 2006, 318(1):63-76. 10.1016/j.jmaa.2005.05.021Elayi S, Zhang S: Stability and periodicity of difference equations with finite delay. Funkcialaj Ekvacioj 1994, 37(3):401-413.
Kipnis M, Komissarova D: Stability of delay difference system. Advances in Difference Equations 2006, 2006:-9.
Medina R: Stability analysis of nonautonomous difference systems with delaying arguments. Journal of Mathematical Analysis and Applications 2007, 335(1):615-625. 10.1016/j.jmaa.2007.01.053
Pituk M: Convergence and uniform stability in a nonlinear delay difference system. Mathematical and Computer Modelling 1995, 22(2):51-57. 10.1016/0895-7177(95)00110-N
Pituk M: Global asymptotic stability in a perturbed higher-order linear difference equation. Computers & Mathematics with Applications 2003, 45(6–9):1195-1202.
Schinas J: Stability and conditional stability of time-dependent difference equations in Banach spaces. Journal of the Institute of Mathematics and Its Applications 1974, 14(3):335-346. 10.1093/imamat/14.3.335
Zhang S: Estimate of total stability of delay difference systems. Computers & Mathematics with Applications 1999, 37(9):31-38. 10.1016/S0898-1221(99)00111-X
Kuruklis SA:The asymptotic stability of
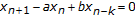 . Journal of Mathematical Analysis and Applications 1994, 188(3):719-731. 10.1006/jmaa.1994.1457
. Journal of Mathematical Analysis and Applications 1994, 188(3):719-731. 10.1006/jmaa.1994.1457Shahruz SM, Schwarz AL: An approximate solution for linear boundary-value problems with slowly varying coefficients. Applied Mathematics and Computation 1994, 60(2-3):285-298. 10.1016/0096-3003(94)90110-4
Qu R, Agarwal RP: Improved error bounds for freezing solutions of linear boundary value problems. Applied Mathematics and Computation 1998, 94(2-3):97-112. 10.1016/S0096-3003(97)10067-4
Gil MI, Medina R: The freezing method for linear difference equations. Journal of Difference Equations and Applications 2002, 8(5):485-494. 10.1080/10236190290017478
Acknowledgments
The author thanks the referees of this paper for their careful reading and insightful critiques. This research was supported by Fondecyt Chile under Grant no. 1.070.980.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Medina, R. Absolute Stability of Discrete-Time Systems with Delay. Adv Differ Equ 2008, 396504 (2007). https://doi.org/10.1155/2008/396504
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/396504

 ;
; 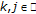 and
and 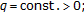
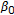 =
=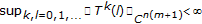 ,
, 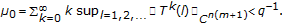
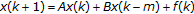 with commutative matrices. Journal of Mathematical Analysis and Applications 2006, 318(1):63-76. 10.1016/j.jmaa.2005.05.021
with commutative matrices. Journal of Mathematical Analysis and Applications 2006, 318(1):63-76. 10.1016/j.jmaa.2005.05.021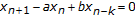 . Journal of Mathematical Analysis and Applications 1994, 188(3):719-731. 10.1006/jmaa.1994.1457
. Journal of Mathematical Analysis and Applications 1994, 188(3):719-731. 10.1006/jmaa.1994.1457